塇崟嶳惔戧帥乮堬忛導拀惣巗乯丂丂 丂丂丂丂丂丂
乷尨暥乸
崱桳擛恾墌戜撪梕峛壋榋媴廩撪柍摦峛媴宎庒姳壋媴宎庒姳栤摼忋宎弍擛壗
摎濰 擛嵍弍丂丂丂弍濰埲壋宎尭峛宎梋敿擵柤栘帺擵埲尭峛壋宎憡忔擇抜梋嶰彍擵暯曽奐擵壛栘柤壩尭栘柤搚
擵壩彍搚柤嬥壛堦屄柤悈帺擵撪尭嬥梋暯曽奐擵壛悈忔壋宎堊幚仜抲嶰屄暯曽奐擵埲彍幚摼忋宎崌栤 丂丂丂
恾偺傛偆偵丄墌悕戜偺撪偵峛壋俇偮偺媴偑愙偟偰摦偐側偄傛偆偵偁傞丅偙偙偱丄峛媴偺捈宎偲壋媴偺捈宎偲傪梡偄偰墌悕戜偺
忋掙偺墌偺捈宎傪媮傔傞曽朄偼丄偳偺傛偆偱偁傞偐丅
亂寁嶼曽朄亃丂峛媴偺捈宎偐傜壋媴偺捈宎傪堷偒丄偦傟傪俀偱妱偭偨傕偺傪栘偲柤晅偗傞丅
栘偺俀忔傪峛壋媴偺捈宎傪妡偗崌傢偣偰俀攞偟偨傕偺偐傜堷偒丄偦傟傪俁偱妱偭偰
暯曽偵奐偄偨傕偺偵栘傪懌偟偨寢壥傪壩偲柤晅偗丄栘傪堷偄偨寢壥傪搚偲柤晅偗傞丅
搚傪壩偱妱偭偨寢壥傪嬥偲柤晅偗傞丅嬥偵侾傪懌偟偨寢壥傪悈偲柤晅偗傞丅
悈傪俀忔偟偰偦偙偐傜嬥傪堷偄偨傕偺傪暯曽偵奐偒丄偦傟偵悈傪懌偟偨傕偺偵壋媴偺捈宎傪妡偗偨寢壥傪俁傪暯曽偵奐偄偨悢
偱妱傟偽墌悕戜偺忋掙偺墌偺捈宎偑媮傔傜傟傞丅丂丂
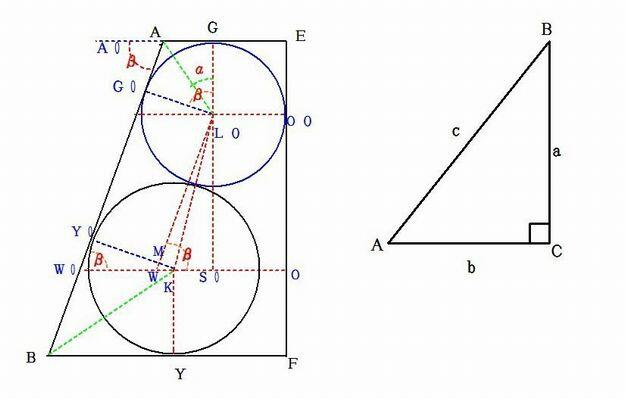
峛媴傪俲乮倠乯丆俲2乮倠乯丆俲3乮倠乯丆壋媴傪 俴乮L乯墌悕戜偺忋掙偺墌偺捈宎俙俢亖倶 偲偡傞丅
俲2乮倠乯丆俲3乮倠乯媴偺愙慄俿偲俴偲偺嫍棧俴俿偼
俴俿亖1/2併L丱2亄2KL
傑偨俁峛媴偺廳怱傪俷丆俁壋媴偺廳怱傪俷1偲偡傞丅
俷俿亖併俁倠乛俇 俷乫俴亖併俁L乛俁丂偱偁傞偐傜
俴俽亖俴俿丱2亅俿俽丱2亖俴俿丱2亅乮俷俽亅俷俿乯丱2亖
乮乮L丱2亄2KL乯乛係乯亅乮乮併俁乮俀L亅K乯乛俇乯丱2亖乮侾侽KL亅K丱2亅L丱2乯乛侾俀亖
乮俉KL亅K丱2亄俀KL亅L丱2乯乛侾俀亖俀KL乛俁亅乮乮K亅L乯乛俀乯丱2亊侾乛俁
亂乮K亅L乯乛俀亖俫丂丂偲偡傞亃丂丂俴俽亖併乮俀KL亅俫丱2乛俁乯
墌悕戜偼夞揮戜偱偁傝丄夞揮幉傪俤俥偲偟丄敿夞揮偟偨傕偺傪 俴0 偲偡傞
傑偨墌悕戜偺曣慄俙俛偼丄俲(K)丆俴(L)偺愙慄偲側傞丅
俴0俵倂 偼丄 俙俛 偵暯峴偲偟丄俧俴0 俽0 偼 俲0 偵悅捈偲偡傞丅
墌悕戜偺忋掙偺墌偺捈宎 倶丂偼丂佢俙俴0倁 亖兛 (傾儖僼傽乯丂偲偟偰
倶亖俀乮俙俤乯亖俀乮俙俧亄俧俤乯亖俀乮俧俴0俿倎値兛亄俴0俷0乯丂偱偁傞丒丒丒嘆
仸丂俿倎値兛亖俙俧乛俧俴0丂丂俙俧亖俧俴0亊俿倎値兛
佢俧俴0俧0亖兝 乮儀乕僞乯丂偲偡傞丅丂丂丂兝亖俀兛丂兛亖兝乛俀丂偱偁傝
佢俧俴0俧0亖佢俙0俙俛亖佢俙倂俷0亖兝丂偱偁傞丅
捈妏嶰妏宍俴0俵俲 俴0俲俽0 偵偍偄偰
俴0俵亖們 丂俵俲亖倓丂 俲俽0亖倕 丂俴0俽0亖倖 丂偲偡傞
倓亖(倠亅L)乛俀 亖 俫丂丂倖亖俴俽亖併(俀倠L亅俫丱2)乛俁
倕亖俲0亅俽0俷亖俲0亅俴0俷0亖乮併俁倠乛俁乯亅乮併俁L乛俁乯亖乮併俁乮倠亅L乯乯乛俁亖
俀併俁乛俁亊乮倠亅L乯乛俀亖俀併俁俫乛俁丂丂丂丂丂丂仸 乮倠亅L乯乛俀亖俫
們丱2亖(倖丱2亄倕丱2)亅倓丱2亖(俀倠L亅俫丱2)乛俁亄係俫丱2乛俁亅俁俫丱2乛俁亖
俀倠L乛俁丂丂丂丂丂們亖併乮俀倠L乛俁乯丂
俴0倂亖倫丂丂丂倂俽0亖倯丂偲偡傞丂丂丂丂丂丂丂丂丂亂憡帡婰崋偺丂佷亃
捈妏嶰妏宍俲俵倂佷 俴0俽0倂 丂倂俵丗倂俽0亖俵俲丗俴0俽0丂 乮倫亅們乯丗倯亖倓丗倖丂
倫倖亅們倖亖倯倓丒丒丒嘇丂丂椉曈偵倖傪偐偗傞丂丂丂倯倓倖亖倫倖丱2亅們倖丱2
俲倂丗俴0倂亖俵俲丗俴0俽0 丂丂乮倯亅倕乯丗倫亖倓丗倖丂丂丂丂倯倖亅倕倖亖倫倓丒丒丒嘊丂
椉曈偵倓傪偐偗傞丂丂倯倓倖亖倫倓丱2亄倕倓倖丂丂 倫倖丱2亅們倖丱2亖倫倓丱2亄倕倓倖
倫乮倖丱2亅倓丱2乯亖倕倓倖亄們倖丱2丂丂倫亖乮們倖丱2亄倕倓倖乯乛乮倖丱2亅倓丱2乯丂
嘇幃傛傝丆椉曈偵倓傪偐偗傞丂丂丂丂倓倖倫亖倓丱2倯亄們倓倖丂丂丂
嘊幃傛傝丆椉曈偵倖傪偐偗傞丂丂丂丂倓倖倫亖倯倖丱2亅倕倖丱2丂丂丂丂
倯倖丱2亅倕倖丱2亖倓丱2倯亄們倓倖丂丂乮倖丱2亅倓丱2乯倯亖倕倖丱2亄們倓倖
倯亖乮倕倖丱2亄們倓倖乯乛乮倖丱2亅倓丱2乯
丂丂丂丂丂丂丂丂丂丂丂丂丂亂嶰妏斾偺岞幃亃
tanA=sinA/cosA偺徹柧
恾偺仮俙俛俠偵偍偄偰丄丂倱倝値A亖倎乛們傛傝
倎亖們倱倝値A丂丂丂丂cosA亖倐乛們丂丂倐亖們cosA傛傝
偙偙偱tanA偵偮偄偰峫偊偰傒傞丅
偙傟偵丄偝偒傎偳媮傔偨a=csinA偲b=ccosA傪戙擖偡傞丅
tanA亖倎乛倐亖csinA乛ccosA亖 sinA/cosA
劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒劒
倲倎値兛亖倲倎値兝乛2亖(1-俠倧倱兝)乛俽倝値兝亖乮侾亅倯乛倫乯乛乮倖乛倫乯亖
乮倫乛倖乯亊乮侾亅倯乛倫乯亖乮倫亅倯乯乛倖
倲倎値兛亖乮們倖丱2亄倓倕倖乯乛乮乮倖丱2亅倓丱2乯亅乮倕倖丱2亄們倓倖乯乛乮倖丱2亅倓丱2乯乯乛倖亖
倖{乮乮們倖亄倓倕乯亅乮倕倖亄們倓乯乯乛乮倖丱2亅倓丱2乯}乛倖亖
乮們倖亄倓倕乯亅乮倕倖亄們倓乯乯乛乮倖丱2亅倓丱2乯亖倖乮們亅倕乯亅倓乮們亅倕乯乛乮倖丱2亅倓丱2乯乯亖
倖乮們亅倕乯亅倓乮們亅倕乯乛乮倖亄倓乯乮倖亅倓乯亖乮們亅倕乯乮倖亅倓乯乛乮倖亄倓乯乮倖亅倓乯亖
_______________ ___
乮們亅倕乯乛乮倖亄倓乯亖乮併乮俀倠L乛俁乯亅丂俀併俁俫乛俁乯乛乮倖亄俫乯亖
_______________
乮併乮俀倠L乛俁乯亅丂乮俀俫乛併俁乯乯乛乮倖亄俫乯丒丒丒丒丒嘆偵戙擖偡傞
倶亖俀乮俧俴0俿倎値兛亄俴0俷0乯亖
______________
丂丂 俀乮乮併乮俀倠L乛俁乯亅丂乮俀俫乛俁乯乯乛乮倖亄俫乯乯亊L乛俀亄乮併俁L乛俁乯亖
乮併俀倠L亅丂俀俫乯乛併俁乮倖亄俫乯乯亄俀乛併俁乯L亖
乮乮併俀倠L亅丂俀俫亄俀倖亄俀俫乯乛併俁乮倖亄俫乯乯L亖
乮乮併俀倠L亄俀倖乯乛併俁乮倖亄俫乯乯L丒丒丒嘋丂丂倖亄俫亖俧丂偲偡傞
併俁倶乛L亖乮併俀倠L亄俀倖乯乛俧
丂丂倖亖併(俀倠L亅俫丱2)乛俁亖
倖丱2亖(俀倠L亅俫丱2)乛俁丂丂俀倠L亖俁倖丱2亄俫丱2丂丂
_______________
嘋幃偼丂併俁倶乛L亖(併俁倖丱2亄俫丱2乯亄俀倖)乛俧亖
________________________________________________________________
((併倖丱2亅俀倖俫亄俫丱2亄倖丱2亅俫丱2亄倖丱2亄俀倖俫亄俫丱2乛俧丱2乯
亄((倖亅俫)亄(倖亄俫))乛俧亖乮併乮(倖亅俫)丱2乛俧丱2乯亄乮乮倖亅俫乯乮倖亄俫乯乛
俧丱2乯乯亄(倖亄俫)丱2乛俧丱2乯亄((倖亅俫)亄(倖亄俫))乛俧 丂倖亅俫亖俰丂偲偡傞
________________________________________________
併乮俰乛俧乯丱2亄乮俰乛俧乯乮俧乛俧乯亄(俧乛俧)丱2亄俰乛俧亄俧乛俧 俰乛俧亖俹丂偲偡傞
_______________ 丂丂丂丂丂丂 _____________________
併俹丱2亄俹亄侾亄俹亄侾併俹丱2亄俀俹亄侾亅俹亄俹亄侾 俹亄侾亖俻丂偲偡傞
併俻丱2亅俹亄俻 倶亖乮乮併俻丱2亅俹亄俻乯乯L 乛併俁