�Q�n���@�k��_�Ёi�Z�z�j
�o�����p
���L�@�}�~�V���u��~�j�����~�j���]���~���Z�a�e����~�a��⓾��~�a�p�@��
���H �@���p�@�@�@�p�H�Z�a�ȏ����a�揬�~�a���V���Z�a㰈Ȍ����a㰗]���~�a��i�ȏ��V����~�a���� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
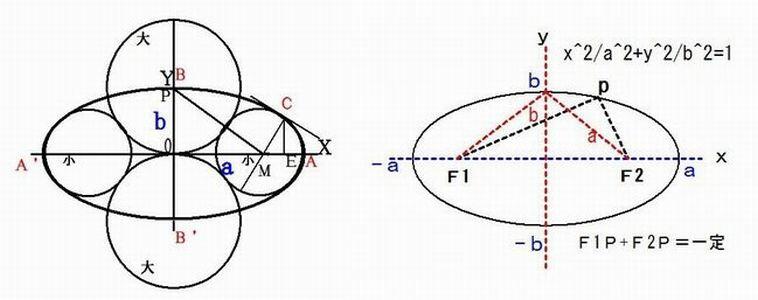
�}�̂悤�ɁA�ȉ~�̓��ɑ�~�Q�Ƃ���ɋ��܂��悤�ɏ��~�Q�Ƃ�����B�����őȉ~�̒����ƒZ���Ə��~�̒��a�Ƃ�
�p���āA��~�̒��a�����߂���@�͂ǂ̂悤�ł��邩�B
�@�@�@�@�@ �@�@�@ �@�y�ȉ~�̕������̕W���`�z
���@a>b>0 �̂Ƃ��C������
���ȉ~�̒�`
�e1�o+�e2�o���@���̒���(2a) �����_P�̋O�Ղ̂��Ƃ�ȉ~�Ƃ����D�����ā@�e1�C�e2 �̂��Ƃ��œ_�Ƃ����D
�ȉ~�̕������i�W���`�j�́@x^2/a^2+y^2/b^2=1�@�ƕ\�����D
�œ_ �e1�̍��W�F (-���C�O)=(-��a^2-b^2,0) �œ_ �e2�̍��W�F (���C�O)=(��a^2-b^2,0)
�����̒����F 2a �Z���̒����F 2b �ƂȂ�D
���ȉ~�̕������̓��o
�_P�̍��W�� (x,y) �Ƃ���� �e1�o+�e2�o��2a �̊W���C
(��(x+f )^2+y^2)+(��(x-f )^2+y^2)��2a (��(x+f )^2+y^2)��2a-(��(x-f )^2+y^2)
���ӂ�2�悵�āC��������ƁC (x+f )^2+y^2)��4a^2-4a��(x-f )^2+y^2+(x-f )^2+y^2
a��(x-f )^2+y^2= a^2-xf a^2{(x-f )^2+y^2}= a^4-2a^2xf +x^2f^2
(a^2-f^2)x^2+a^2y^2= a^2(a^2-f ^2 ) ���ӂ�a^2(a^2-f ^2 ) �Ŋ���ƁC
x^2/a^2+y^2/(a^2-f ^2 )=1 b^2+f^2=a^2 ��� x^2/a^2+y^2/b^2=1 �ƂȂ�A �ȉ~�̕������̕W���`�����܂�B
�@�@�@�@�@ �y�ȉ~�̖@���̕������z
�ȉ~�Fx^2/a^2+y^2/b^2=1 ��̓_ A(x0,y0)A(x0,y0) �ɂ�����@���̕������́C
y0/b^2(x-x0) - ��0/��^2(��-��0)= 0
�y�������߂���@�z
�ȉ~���@�n�i�j���Q���C�k���Q���j�@��~���@�o�i�����Q���j�@���~���@�l�i�����Q���j�@�Ƃ���B
�n�����_�A�n�`���w���A�n�a���x���Ƃ���B�@�ȉ~�̕������́@�@x^2/a^2+y^2/b^2=1
�ȉ~��̂b( S, T)�̂x���W��T�� �r^2/a^2+�s^2/b^2=1 �r^2b^2 �{�s^2= a^2b^2
�s^2��b^2( a^2�|�r^2�j�^a^2 �E�E�E�E�E�@
�_�b��ʂ�@���̕������́@�@�@�@a^2x/ �r �|b^2y/�s�� a^2�|b^2�@�ł���A���̖@����
���ډ~ �l �̒��S(���C�n)��ʂ邩�� �@a^2��/ �r �� a^2�|b^2�@�@
���@^2�����r (a^2�|b^2) �r��a^2��/ (a^2�|b^2) �E�E�E�E�E�A
���p�O�p�`�b�d�l�ɂ����ā@�@�b�l^2���b�d^2�{�l�d^2�@�@��^2���s^2�{�i�r�|���j^2
�@���������ā@�@�@�@��^2��b^2( a^2�|�r^2�j�^a^2�{�i�r�|���j^2
�A���������ā@�@�@�@��^2��(b^2( a^2�|(a^2��/ (a^2�|b^2)))�^a^2�{�ia^2��/ (a^2�|b^2)�|��^2)
a^2(a^2�|b^2)^2��^2��a^2b^2(a^2�|b^2)�|a^2b^2��^2�{a^2b^2��^2��
a^2b^2(a^2�|b^2)�|a^2b^2��^2(a^2�|b^2) (a^2�|b^2)��^2��b^2(a^2�|b^2)�|b^2��^2
b^2��^2��b^2(a^2�|b^2)�| (a^2�|b^2)��^2��(a^2�|b^2)(b^2�|��^2) ��^2��((a^2�|b^2)(b^2�|��^2))�^b^2
����(��((a^2�|b^2)(b^2�|��^2)))�^b��(��((K^2�|L^2)(L^2�|M^2)))�^2L
���p�O�p�`�o�n�l�ɂ����ā@�@�o�l^2���o�n^2�{�n�l^2�@ �i�o �{���j^2 �� �o^2�{��^2
(x^2�^2�{M^2�^2)��(x^2�^2)�{(K^2�|L^2)(L^2�|M^2)�^4L^2
L^2x^2 �{ �QL^2Mx �{ L^2M^2 �� L^2x^2 �{ K^2L^2�|K^2M^2 L^4
2Mx�� K^2�|K^2M^2�^ L^2�|L^2�� K^2�|((K�^ L)M^2)�|L^2 x �� ((K^2�|((K�^ L)M^2)�{L^2)�^ 2M
�ȉ~�̒������@K���Qa�A�Z���@L���Qb�A�ȉ~�ɂQ�_�œ��ڂ���~�̒��a���@M ���Q���@�@
�ȉ~�̒��S�Ɠ��ډ~�̒��S�Ƃ̋�����������B
����(��((K^2�|L^2)(L^2�|M^2)))�^2L ����(��((a^2�|b^2)(b^2�|��^2)))�^b