
前回の予告通り、今回は二分探索木というものについて話します。さて、これは一体何なのでしょうか?
今回の要点は以下の通りです。
では、いってみましょう。
今回は二分探索木のお話です。二分探索木という名前から予測がつくように、これは二分木の一種です。
簡単に言うとどんなものかというと、ある要素を簡単に探し出すことができる二分木です。どういう風にすれば実現できるでしょうか? ちょっと考えながら話を進めてみましょう。
ある要素を簡単に探すといえば、二分探索(第30章参照)が先ず思い浮かびます。これをヒントに考えていくとしましょう。
先ず、二分探索では配列をソートします。そして、真ん中の要素(厳密にはど真ん中である必要はありません)の値と探したい値とを比較します。で、大きいか小さいかで次に探査する場所を決めます。そして、等しくなるまでこれを続けるというものでした。
二分探索の重要な部分は「ソートされた配列を使う」ということと、「比較を利用する」というところです。この部分を二分木に適用してみましょう。
先ず、「比較」を利用してみましょう。二分木のノードは、次の要素2つだけ持っています。そう、2つです。ということは、そのノードにある値と探したい値とを比較して、大きければ右、小さければ左へ行くということができそうです。木が変に偏った形をしていなければ、この探し方ができればどの要素も安定した速度で見つかるはずです。
では、この探し方のできる二分木に要求される特徴は、あるノードの右の子以降にはそのノードの値よりも大きい値しか入ってなく、左の子以降にはそのノードの値よりも小さい値しか入っていないことです。これは「配列がソートされている」という状態に対応していると考えることができます。
このような、いわゆる「ソートされた」二分木を作るのはとても簡単です。探すときと同じ事をして、その最後に要素を追加すればいいだけです。つまり、そのノードにある値と追加したい値とを比較して、大きければ右、小さければ左へ行き、ノードのない部分に到達したらそこにノードを追加すればいいということです。
こういう風に作った二分木は「ソートされた」二分木となり、「比較を使って」簡単にある値を持つノードを探し当てることができます。これが二分探索木です。
文だけでは何なので、ちょっと例を見てみましょう。
 |
先ず、二分木に値3を追加します。左の図のような感じですね。
では、これに6を追加してみましょう。先ず、6をルートの値3と比べます。6は3よりも大きいので、右に進むことにします。ここでもうノードがなくなっているので、ここにノードを追加することにしましょう。
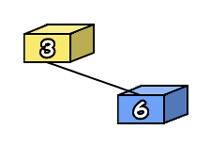 |
こんな感じです。
今度は1を追加します。先ず、同じように1をルートの値3と比べます。1は3よりも小さいので、左に進むことにします。ここでもうノードがなくなっているので、ここにノードを追加します。
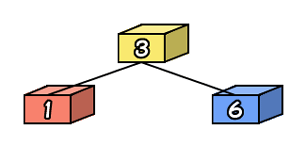 |
こんな感じです。
同じようにして、今度は2と5を追加します。先ずは2です。2は3よりも小さいので、最初は左に進みます。そして、2を次にある値1と比べます。2は1よりも大きいので右に進みます。ここでノードがなくなったのでここに追加します。
次は5です。5は3よりも大きいので、最初は右に進みます。そして、5を次にある値6と比べます。5は6よりも小さいので左に進みます。ここにノードを追加します。
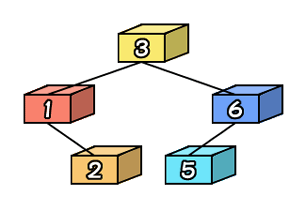 |
こんな感じです。
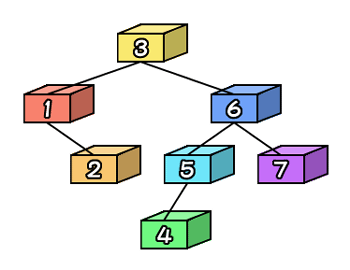 |
同じように4と7を追加すると左のようになります。よくみると、左から値が順番通りに並んでいることが分かります。これが「ソートされた」状態な訳です。
では、実際にプログラムを組んでみましょう。
| プログラム |
|---|
// BinTree1.cpp
#include <iostream.h>
#include <iomanip.h>
#include <string.h>
#include <malloc.h>
// 入力バッファの最大サイズ
const int BUFSIZE = 1024;
// ノード
struct SNode
{
char* id;
int num;
SNode* pChild[2];
};
// 値の入力
bool InputValue(SNode*& pRoot);
// 値を探す
bool FindValue(SNode* pRoot);
// 二分探索木の操作
// ノードの初期化
bool InitNode(SNode* pNode, const char* id, int num);
// ノードの追加(再帰)
bool AddNode(SNode*& pRoot, const char* id, int num);
// ノードを探す(再帰)
SNode*& FindNode(SNode*& pRoot, const char* id);
// 木を表示する
void DispTree(SNode* pRoot);
// 木を表示する(再帰サブルーチン)
void Rec_DispTree(SNode* pRoot, int nDepth);
// 木を解放(再帰)
void FreeTree(SNode* pRoot);
// ノードを解放
void FreeNode(SNode* pNode);
int main()
{
SNode* pRoot = NULL;
while(InputValue(pRoot));
while(FindValue(pRoot));
DispTree(pRoot);
FreeTree(pRoot);
return 0;
}
// 値の入力
bool InputValue(SNode*& pRoot)
{
char id[BUFSIZE];
int num;
cout << "文字列と値を入力して下さい > " << flush;
cin >> id >> num;
if(strcmp(id, "q") == 0 || num == -1)
return false;
return AddNode(pRoot, id, num);
}
// 値を探す
bool FindValue(SNode* pRoot)
{
char id[BUFSIZE];
cout << "ID文字列を入力して下さい > " << flush;
cin >> id;
if(strcmp(id, "q") == 0)
return false;
SNode*& pFind = FindNode(pRoot, id);
if(pFind == NULL)
cout << "見つかりません。" << endl;
else
cout << "値は " << pFind->num << " です。" << endl;
return true;
}
// 二分探索木の操作
// ノードの初期化
bool InitNode(SNode* pNode, const char* id, int num)
{
// strdup は文字列を複製する関数です
// このとき、メモリを確保します
// このメモリの解放は free という関数で行います
pNode->id = strdup(id);
if(pNode->id == NULL)
return false;
pNode->num = num;
for(int i = 0; i < 2; i++)
pNode->pChild[i] = NULL;
return true;
}
// ノードの追加(再帰)
bool AddNode(SNode*& pRoot, const char* id, int num)
{
SNode*& pAdd = FindNode(pRoot, id); // 追加位置を探します
// 既にノードがある場合は上書きします
if(pAdd != NULL)
{
pAdd->num = num;
return true;
}
// ノードを確保します
pAdd = new SNode;
if(pAdd == NULL)
return false;
// ノードを初期化します
if(!InitNode(pAdd, id, num))
{
// 失敗したら解放します
FreeNode(pAdd);
pAdd = NULL;
return false;
}
return true;
}
// ノードを探す(再帰)
SNode*& FindNode(SNode*& pRoot, const char* id)
{
// 見つからなかったらそのまま返す
if(pRoot == NULL)
return pRoot;
// 比較
int fComp = strcmp(pRoot->id, id);
// 見つかったらそのノードを返す
if(fComp == 0)
return pRoot;
// 次のノードに進む
return FindNode(pRoot->pChild[fComp < 0], id);
}
// 木を表示する
void DispTree(SNode* pRoot)
{
Rec_DispTree(pRoot, 0);
}
// 木を表示する(再帰サブルーチン)
void Rec_DispTree(SNode* pRoot, int nDepth)
{
if(pRoot == NULL)
return;
Rec_DispTree(pRoot->pChild[0], nDepth + 1);
cout << setw(nDepth * 2) << "" << pRoot->id
<< " : " << pRoot-> num << endl;
Rec_DispTree(pRoot->pChild[1], nDepth + 1);
}
// 木を解放(再帰)
void FreeTree(SNode* pRoot)
{
if(pRoot == NULL)
return;
// 子ノードを解放してから
for(int i = 0; i < 2; i++)
FreeTree(pRoot->pChild[i]);
// 自分を解放する
FreeNode(pRoot);
}
// ノードを解放
void FreeNode(SNode* pNode)
{
// strdup で確保した領域は free で解放します
// free は malloc という関数で確保したメモリを解放するための関数です
// C言語には new はなく、malloc 関数を使ってメモリを確保します
// strdup はC言語の時代の関数なので、内部で malloc を使っています
free(pNode->id);
// free と delete が混在するのは
// ちょっと気持ちが悪いですね(汗)
delete pNode;
} |
文字列と値を入力して下さい > 最近は 1
文字列と値を入力して下さい > 動的確保とか 2
文字列と値を入力して下さい > 再帰関数とか 3
文字列と値を入力して下さい > バンバン使ってるけど 4
文字列と値を入力して下さい > どうでしょうか? 5
文字列と値を入力して下さい > もうそろそろ 6
文字列と値を入力して下さい > 慣れてきましたか? 7
文字列と値を入力して下さい > q -1
ID文字列を入力して下さい > バンバン使ってるけど
値は 4 です。
ID文字列を入力して下さい > 慣れてきましたか?
値は 7 です。
ID文字列を入力して下さい > ぼちぼちやっていきましょう
見つかりません。
ID文字列を入力して下さい > q
どうでしょうか? : 5
もうそろそろ : 6
バンバン使ってるけど : 4
慣れてきましたか? : 7
再帰関数とか : 3
最近は : 1
動的確保とか : 2 |
はい。こんなもんですね。
この例を見て分かると思いますが、二分探索木はバランスが悪くなるときもあります。「もうそろそろ」を探し出すには5回の比較が必要になってしまいます。もし、一番バランスが良ければ、全部で7つの要素があるので、最大でも3回の比較で済みます。反対に、ソートされた配列の先頭から二分探索木に順番に値を追加していくと、バランスは最悪になります。どんな場合においても必ず効率がいいという保証がないのが、二分探索木のちょっとした弱みになっています。
しかし、ソートされたデータを追加するときに注意しさえすれば、それほどデータが偏ることはないと思います。上の例でも、もっと追加していけばあまり偏りの気にならない状態になるでしょう。
では、今回の要点です。
今回のような探索の速いデータ構造というものは、他にもいくつか考案されています。次回はそのうちでも有名なあるデータ構造を紹介したいと思います。それでは。
Last update was done on 2001.2.10
この講座の著作権はロベールが保有しています