 |
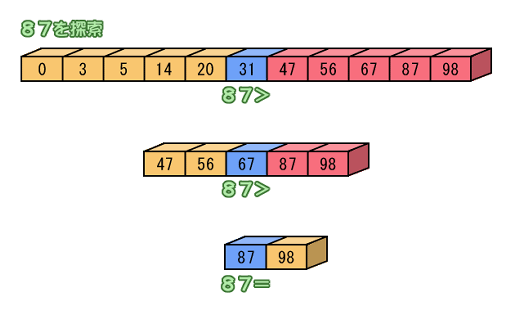
| 図.1 二分探索 |
|---|
今回は、ソートされた配列の中からある値を見つけだすということをします。地道な方法と、速い方法とを比べてみましょう。
それでは、今回の要点です。
では、いってみましょう。
あるソート列を用意してみます。その中からある値を見つけだしたいと思います。
簡単に考えれば、先頭から順に探していけばいいですね。この探索方法を線形探索と呼びます。しかし、探す配列が小さければその速度も気になることはありませんが、配列が非常に大きくなってくるとちょっと気になります。
そこで、高速に探索する方法があります。それが二分探索(バイナリサーチ)です。
先ず、配列が昇順でソートされているとします。そして、見つけたい値と、配列の中央の要素とを比較します。
これで見つかればめっけものですが、そうはいかないことが多いでしょう。その場合、配列の要素よりも大きいか、小さいか、ということになります。
もう分かった人もいるかもしれませんが、配列は昇順ソートされているので大きいときはそれ以降に、小さいときはそれ以前にしか目的の要素はありません。降順ならその逆ですね。
ということは、値を探す場所は配列全体の半分でよくなります。
次に、またこの半分の所の中央の要素と比較します。すると、また探索範囲は半分になります。これを、値が見つかるまで続ければ探索完了です。探索範囲をどんどん半分にしていくので、二分探索という名前が付いています。
この方法をちょっと図にしてみましょう。
 |
| 図.1 二分探索 |
|---|
二分探索には bsearch という関数が用意されています(stdlib.h ヘッダファイルが必要です)。
void* bsearch(const void* pKey, const void* pBase, size_t num, size_t width,
int (*fpCompare)(const void* pElem1, const void* pElem2));
pKey には探す値を入れている変数のアドレスを、pBase には配列を、num には配列の要素数を、width には1要素のサイズを渡します。そして fpCompare には qsort と同じく比較関数を渡します。使い方は qsort とほとんど同じなので、詳しい説明は割愛します。
普段は(バグの可能性を無くすために)これを使うことを奨めます。ですが、今回は敢えて二分探索ルーチンを作ってみましょう。
配列の中に2つ以上同じ値があるとどれをとっていいか分からなくなるので、配列は同じ値が2度出ないように作ります。
| プログラム |
|---|
// Bsearch1.cpp
#include <iostream.h>
#include <stdlib.h>
#define numof(array) (sizeof (array) / sizeof *(array))
void SetData(int* pnData, int nNumOf);
bool InputAndSearch(int* pnData, int nNumOf);
int BinSearch(int num, const int* pnData, int nNumOf);
int main()
{
int anData[1024];
SetData(anData, numof(anData));
while(InputAndSearch(anData, numof(anData)));
return 0;
}
// 昇順ソートされたデータのセット
void SetData(int* pnData, int nNumOf)
{
int i;
pnData[0] = 1;
for(i = 1; i < nNumOf; i++)
{
// 1〜5の値を前の要素に足します
pnData[i] = pnData[i - 1] + (rand() % 5 + 1);
}
}
// 入力と探索
bool InputAndSearch(int* pnData, int nNumOf)
{
int nSearch; // 探す値
int iResult; // 探索結果
cout << "探す値を入力して下さい > " << flush;
cin >> nSearch;
if(nSearch <= 0)
return false;
iResult = BinSearch(nSearch, pnData, nNumOf);
if(iResult == -1)
cout << "見つかりませんでした..." << endl << endl;
else
cout << iResult + 1 << " 番目に見つかりました! ("
<< pnData[iResult] << ")" << endl << endl;
return true;
}
// 二分探索
// 探す値、配列、要素数を渡します
// 見つからなければ -1 を返します
int BinSearch(int num, const int* pnData, int nNumOf)
{
int iFirst = 0; // 探索範囲の最初の要素
int iLast = nNumOf - 1; // 探索範囲の最後の要素
int iComp; // 比較する要素
int nComped; // 比較結果
// 探索範囲がなくなったら終了
while(iLast - iFirst > 0)
{
iComp = (iFirst + iLast) / 2; // 平均値をとる
nComped = pnData[iComp] - num;
// 要素との差が0なら探索終了
if(nComped == 0)
return iComp;
// 探す値の方が大きいときは、iFirst を進める
if(nComped < 0)
iFirst = iComp + 1;
// 逆の時は iLast を戻す
else
iLast = iComp - 1;
}
// iLast が iFirst の前にきてしまったとき、
// もしくは残った要素と探す値が一致しないとき、
// 配列にはその要素は存在しない
// ショートサーキット(第2章参照)を使っている点にも注意
if(iLast - iFirst < 0 || pnData[iFirst] != num)
return -1;
return iFirst;
}
|
| 実行結果例 |
探す値を入力して下さい > 342 112 番目に見つかりました! (342) 探す値を入力して下さい > 383 見つかりませんでした... 探す値を入力して下さい > 888 293 番目に見つかりました! (888) 探す値を入力して下さい > 475 見つかりませんでした... 探す値を入力して下さい > 0 |
確かに探索できているようですね。
二分探索を使うと、例え配列の要素数が232(4294967296)という巨大なものであっても、最悪33回で探索が完了します。
探索領域は1回につき半分になるわけですから、232は231になります(正確には比較した要素を除くので少しずれます)。2回目には230、3回目には229となり、結局31回目には21=2となり、32回目に1となります。最後に、その1つを探索して終わりです。
配列の一番最後に目的の要素がある時を考えると、地道に最初から探していると232回目に見つかることになります。最悪232回ということです。平均でも231回です。二分探索を使えば最悪33回で、劇的な差があることがあります。
232というあり得ないほど大きな配列でさえ最悪33回で見つかるのですから、普通の配列ならもっと速く見つかるわけです。N要素の配列を探索するとき、最悪でも [log2N] + 1 回、つまりC/C++でいうところの (int)(log(N) / log(2)) + 1 回で見つかります。2の何乗に近いかを考えて、最悪でもその値くらいになると考えると分かりやすいでしょう。
例えば、名前で昇順ソートされた会員データ(構造体)の配列があるとします。同姓同名の人は、会員番号順でソートします。会員が10万人いるとするとき、名前と会員番号からある会員のデータを探索したいとすると、先頭から探したのでは大変だということが分かります。しかも、名前、つまり文字列の比較は数値の比較よりも時間がかかります。
そこで二分探索を使うと、10万は216(65536)と217(131072)の間にあるので、最悪でも17回くらいの比較で探索は終了することになります。劇的に処理が減ることが分かりますね。
二分探索を使う時には2点注意することがあります。
1つ目は、もちろんのことですが、配列がソートされていなければならないという点です。常にソートされている保証がなければ、qsort とセットで使うようにするといいでしょう。
ソートできないような状況では二分探索は使えません。おとなしく線形探索を使いましょう。
2つ目は、同じ値の要素が2つ以上あると困るという点です。そのうちのどれに当たるかが分からないのです。見つかった地点から左右に展開して、同じ値がどこからどこまであるかを確認すると良いでしょう。
では、今回の要点です。
それでは、次回まで。
第29章 たのしいソート6 | 第31章 出鱈目? 規則的?
Last update was done on 2000.10.12
この講座の著作権はロベールが保有しています