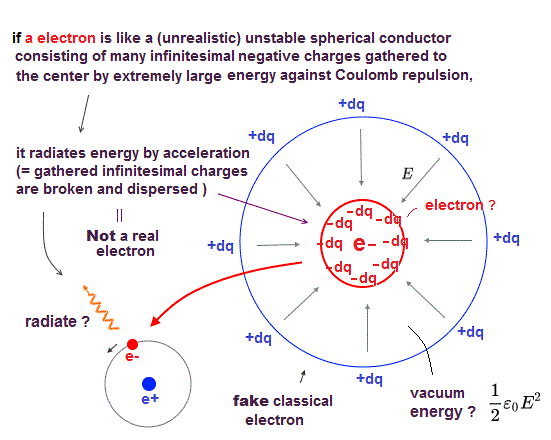
(Fig.1) ↓ "de Broglie wave interference" influences valence electrons' number

The number of valence electrons is fixed in each atom. Helium has two, and Neon has eight valence electrons.
What determines this number of valence electrons ? Electron spin is unrealistic and too weak to affect valence electrons and molecular bonds.
In fact, ( destructive ) interference among electrons' de Broglie waves determines the maximum number of valence electrons in each atom
(Fig.2) ↓ One de Broglie wavelength orbit and its phases
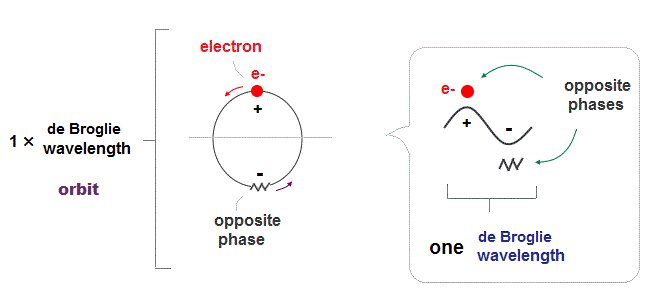
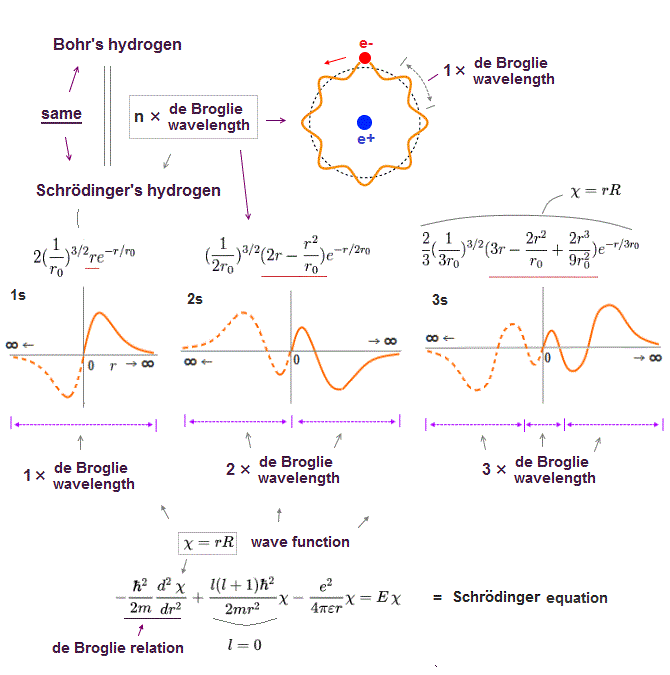
Electron de Broglie wave has been proved in experiments such as Davisson-Germer. One de Broglie wavelength consists of two opposite phases ( crest+ and trough- ).
To avoid destructive interference between these two opposite wave phases, each orbital length has to be an integer times de Broglie wavelength.
(Fig.3) "Opposite" wave phases interfere with each other, destructively. → "perpendicular".
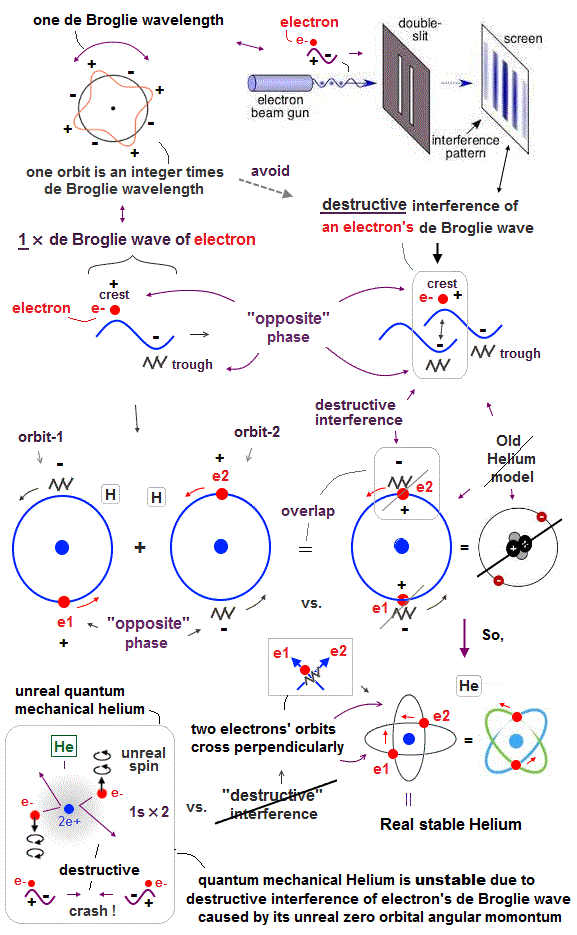
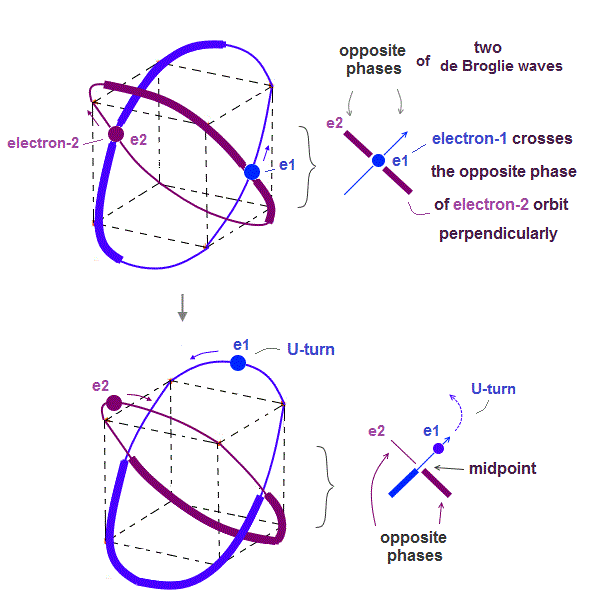
Helium atoms contains two 1 × de Broglie wavelength orbits ( n = 1 ).
Two overlapping opposite wave phases cause "destructive" interference and instability.
To avoid this destructive interference, two orbits of helium have to cross each other "perpendicularly", because "perpendicular" means each wave phase can be independent from another.
(Fig.4) Helium consists of two 1 × de Broglie wavelength orbits.
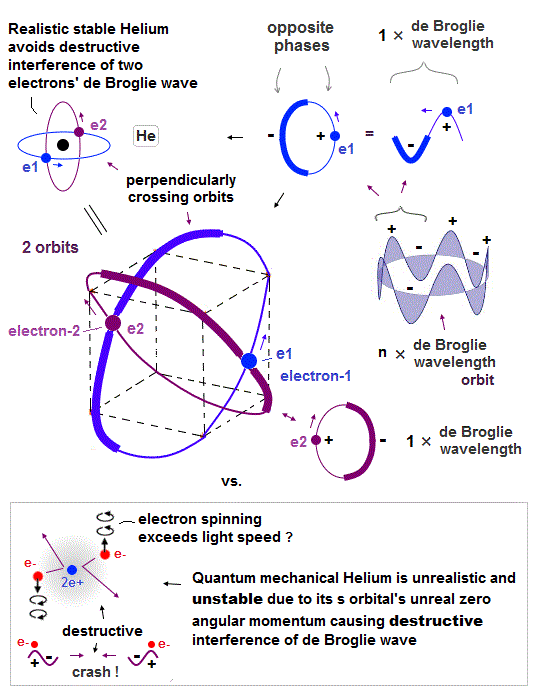
Helium consists of two 1 × de Broglie wavelengt orbits. Fig.4 shows how two electrons are moving in Helium orbits.
To avoid the destructive interference between two de Broglie waves, these electrons' orbits are perpendicular to each other.
(Fig.5) ↓Combining four 1 × de Broglie wavelength orbits. ←Impossible
Helium consists of two 1 × de Broglie wavelength orbits. The maximum orbital number in 1 × de Broglie wavelength is two orbits.
Combining four 1 × de Broglie wavelength orbits in one atom (= Be ? ) is impossible due to destructive interference among electron de Broglie waves.
(Fig.6) ↓ e3 electron is surrounded by opposite wave phases of e1 and e2.
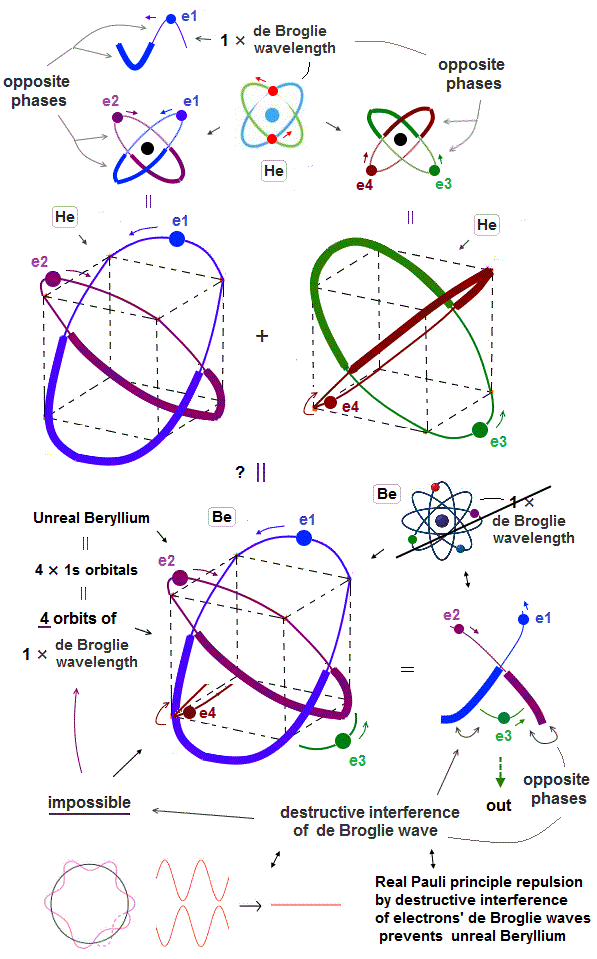
The maxmum orbital number in 1 × de Broglie wavelength is two orbits as seen in Helium. Then, why we cannot mix four 1 × de Broglie wavelength orbits in a single atom ?
In Fig.6, the e3 electron is completely surrounded by the opposite phases of e1,e2 de Broglie waves.
So in this case, this e3 electron is kicked out from the atom due to destructive interference among de Broglie waves.
This is the reason why four orbits in 1 × de Broglie wavelength is impossible.
(Fig.7) ↓ Four 2 × de Broglie wavelength orbits is possible = Neon.
Opposite phases of de Broglie wave have to cross perpendicularly to avoid destructive interference. Neon has four 2 × de Broglie wavelength orbits.
Why is four 2 × de Broglie wavelength orbits is possible, different from 1 × de Broglie wavelength ?
As seen in Fig.7, the e3 electron is on midlines (= the midpoint between two opposite phases ), when it's just between two other orbits.
Midline (= mid-phase ) does not cause destructive interference in electrons. So four 2 × de Broglie wavelength is possible.
(Fig.8) Opposite phase is longer in 1 × de Broglie wavelength (= 1/2 of orbit )
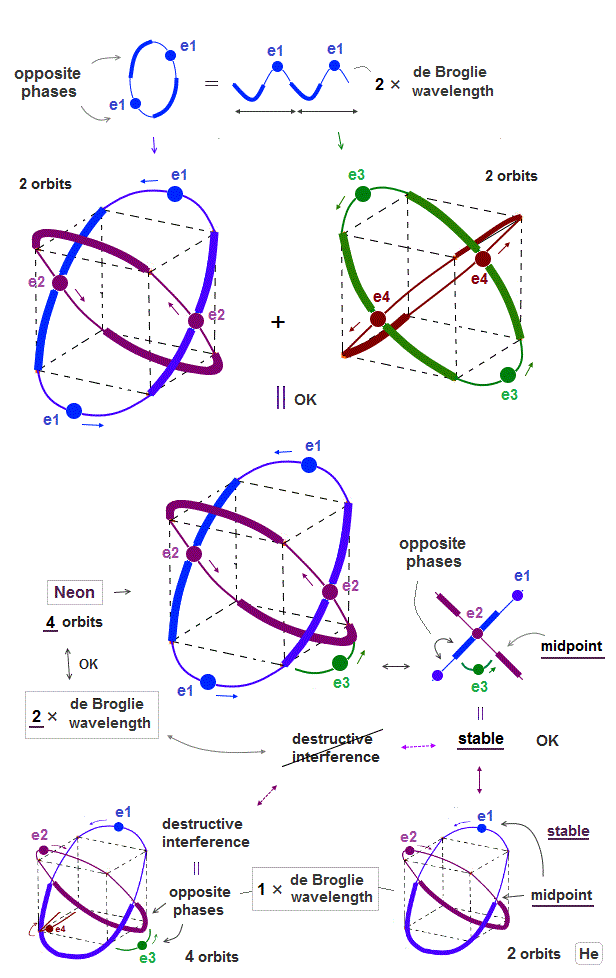
As an atom contains more orbits, the distance between two orbits becomes shorter.
When an electron U-turns between orbits ( see e3 in Fig.7 ), it has to be in other electron's midline (= mid-point ) to avoid destructive interference.
The length of each opposite phase is longer (= 1/2 ) in 1 × de Broglie wavelength than 2 × de Broglie wavelength (= 1/4 ).
So when four 1 × de Broglie wavelength orbits are mixed, each electron are surrounded in opposite phases of other electrons.
As the number of de Broglie wavelength is larger ( 1 → 2 de Broglie wavelength ), it can contain more orbits (= distance between neighboring orbits is shorter ).

2016/11/11 updated. Feel free to link to this site.