Top What determines molecular bond ? π bond
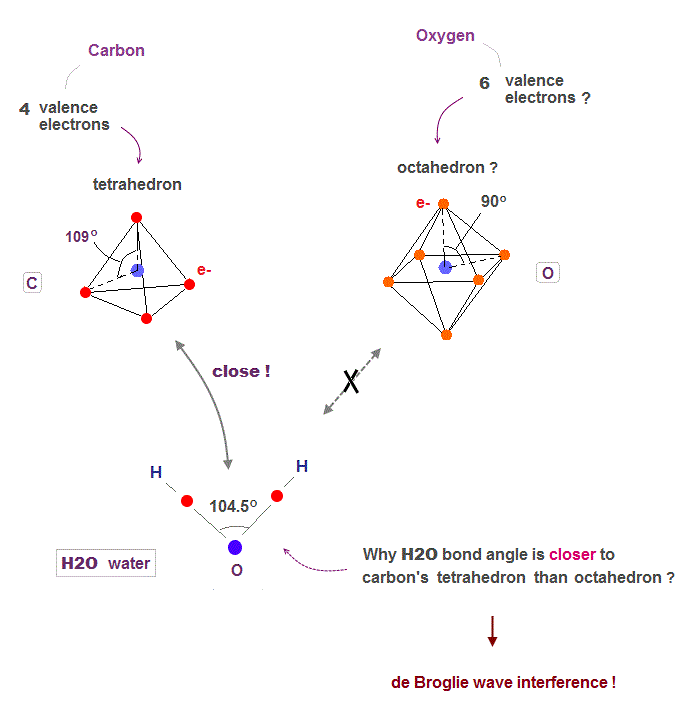
(Fig.1) H-O-H angle is closer to carbon's tetrahedron.

Oxygen has six valence electrons. So it might form octahedral structure with 90 degree bond angle, if we consider only Coulomb repulsion among electrons.
But the H-O-H bond angle of water molecule is 104.5o which is closer to tatrahedron (= 109.5o ) of methane, carbon with four valence electrons.
Unfortunately, the present quantum mechanics cannot show clear reason why H2O angle is not 90o. Instead, we can explain it using de Broglie wave interference.
(Fig.2) ↓ s and p orbitals just show "90o" in oxygen
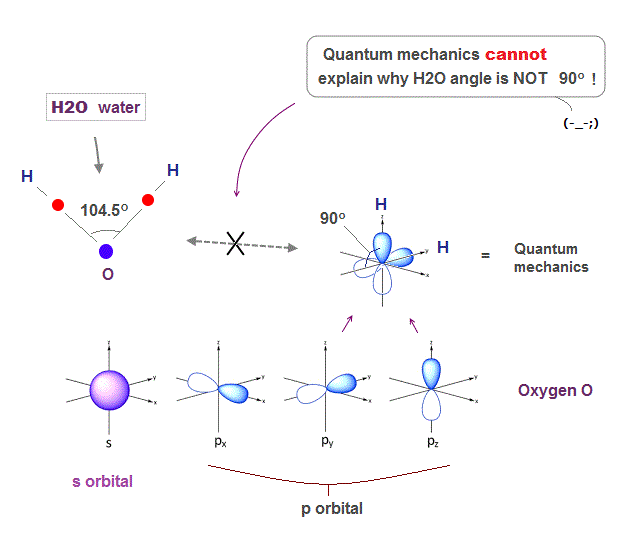
Solving Schrodinger equation gives simple electron orbitals (= s, p .. ) with only right angle (= 90o ).
So basically, quantum mechanics cannot give clear reason why H2O angle in water is NOT 90 degree.
Though physicists try to find a "lame excuse" that only oxygen ( not sulfur ) can form different-type sp orbital. This is too good to be true, and NOT science.
(Fig.3) Unreal spin is really involved in hydrogen molecule bond ?

Textbooks in quantum mechanics often argue that "up" and "down" spins form molecular bonds. But in fact it's physically impossible.
Because spin-spin magnetic interaction (= only 0.001 eV ) is too weak to cause any molecular bonds (= 3-4 eV ). So spin has nothing to do with molecular bonds !
(Fig.4) Point-like electron ( radius r → 0 ), rotation v → ∞

Angular momentum is given by mv × r ( v = velocity, r = radius ).
Electron spin also has angular momentum 1/2ħ, they claim
The problem is an electron is very tiny, point-like.
The point-like particle means its radius r is almost zero.
So to get the angular momentum 1/2ħ, the electron spinning must far exceed light speed ( this p.5, this )
So the electron spin lacks reality.
Even Pauli ridiculed the idea of "spinning electron".
But in "s" orbital of Schrodinger's hydrogen, this electron spin is the only generator of magnetic moment.
So they had no choice but to accept this strange spin ( Not as real spinning and speed ).
(Fig.5) Spin-spin magnetic energy (= 0.0001 eV ) vs. bond energy (= 4.5 eV )
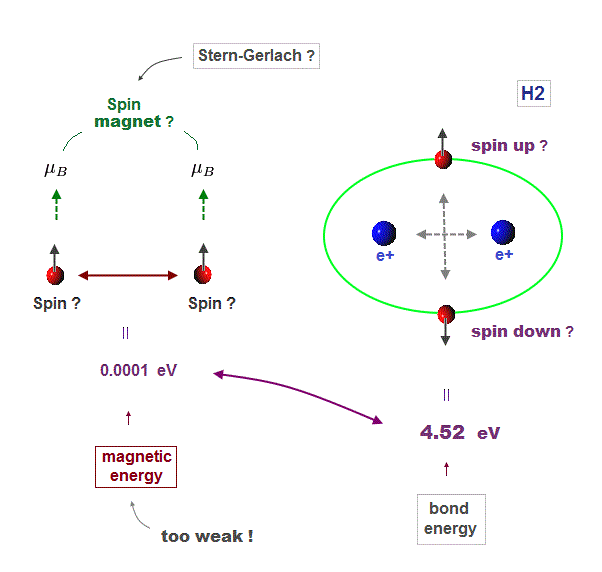
You may hear spin is tiny magnet with the magnitude of Bohr magneton.
We cannot see unreal spin itself, we just measure its magnetism by experiments.
We can replace unrealistic spin by real orbital motion causing the same magnetic field. "Spin" cannot explain actual phenomena.
Spin-spin magnetic interaction is too weak to explain actual ferromagnet.
See this p.6 this p.7. So spin model failed from the beginning.
Hydrogen molecular bond energy is known to be as large as 4.5 eV which electrons spin's magnetic energy (= only 0.0001 eV ! ) can NEVER reach.
(Fig.6) Double-slit experiments proved electron's de Broglie wavelength.
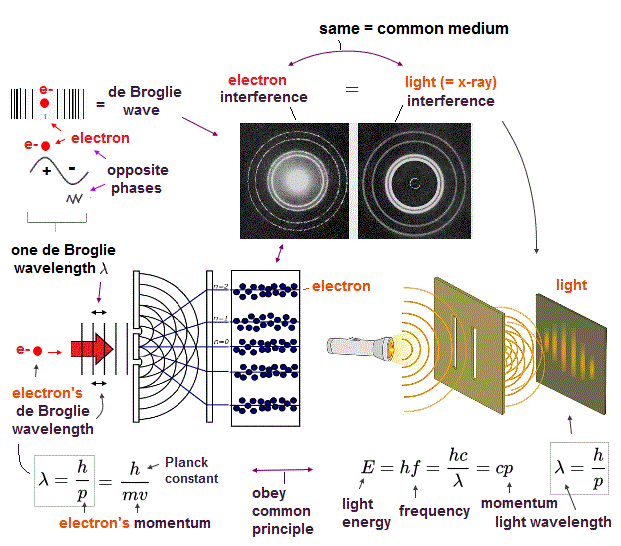
In de Broglie relation, electron's wavelength λ is given by λ = h/mv, where m and v are electron's mass and velocity.
This important matter-wave relation was confirmed in various experiments such as doube-slit, Davisson-Germer and this.
So there is No room for doubt that this de Broglie wave is true.
In these experiments, an electron is driven out from destructive interference regions by the "force" of de Broglie wave ( this p.25 )
This strong "expelling force" by de Broglie wave interference can explain strong Pauli exclusion force and molecular bond !
(Fig.7) Opposite de Broglie wave phases (= ± ) kick out an electron.
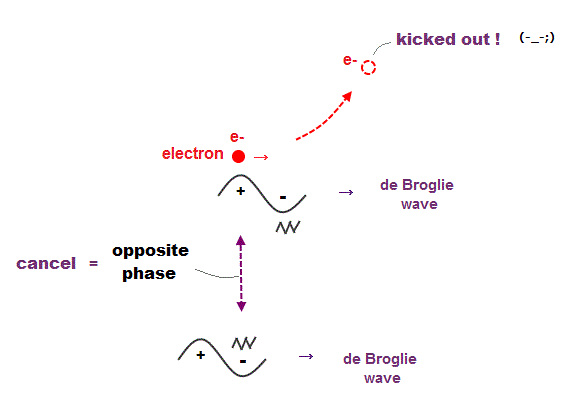
Double-slit experiment showed an electron is de Broglie wave where the opposite wave phses (= ± ) cancel each other.
It means when the opposit wave phases interfere with each other "destructively", the electron is "kicked out" from it.
This strong evidence means the electron's de Broglie wave interference must be actually working in "real" Helium atom casing strong Pauli exclusion principle.
(Fig.8) Quantum orbit satisfies an integer times de Broglie wavelength.
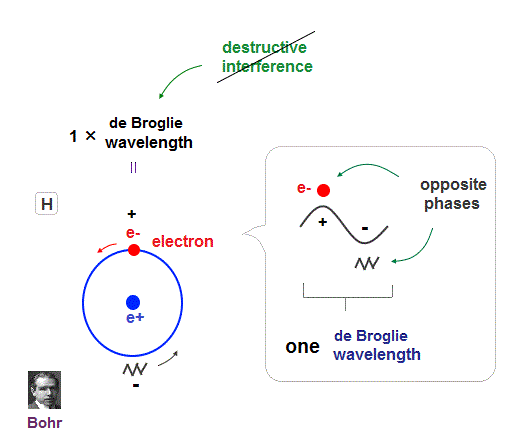
Only Coulomb force is insufficient to explain why atomic energy levels are quantized, and why an electron doesn't fall into nucleus.
Bohr model succeeded in getting actual atomic energies, proposing each orbit is an integer times de Broglie wavelength, as well as Schrodinger's hydrogen .
An integer multiple of de Broglie wavelength means an electron can avoid destructive interference and be stable.
Without this de Broglie wave, each electron can be attracted to positive nuclei, until they stick to each other and its energy is unlimitedly lower !
So the repulsive force by electron's de Broglie wave is strong enough to keep the electron away from the nucleus and cause Pauli exclusion force.
(Fig.9) Electron's de Broglie wave in Schrodinger' hydrogen is destroyed
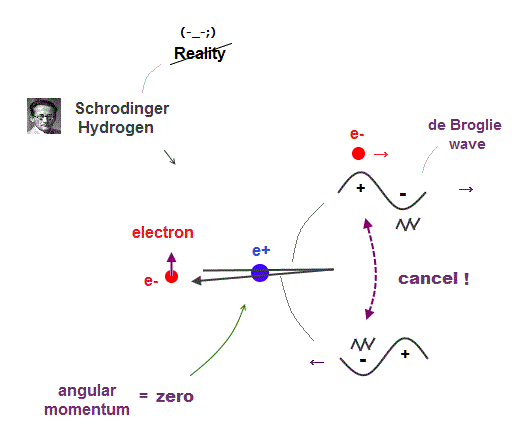
Electron de Broglie wave with experimental proof contradicts quantum mechanical atomic model.
Quantum mechanics claims that electrons in Hydrogen and Helium have zero orbital angular momentum, which means "linear-shaped" orbital.
If so, the opposie phases in electron's de Broglie wave always overlap and interfere with each other "destructively" (= cancel ).
As you see, zero angular momentum in quantum mechanical atoms is inconsistent with de Broglie theory, so false.
(Fig.10) Opposite phases of two de Broglie waves cancel each other

In old Bohr's helium, two electrons are moving on the opposite sides of the nucleus in the same circular orbit (= one de Broglie wavelength ).
Considering Davisson-Germer interference experiment, two electrons of old Bohr's helium are clearly unstable.
1-de Broglie wavelength orbit consists of a pair of the opposite wave phases (= ±ψ ), which cancel each other by destructive interference.
Due to Coulomb repulsion between two electrons, one is always on the opposite side of another where the opposite de Broglie wave phases cancel each other.
Actually, old Bohr's helium of Fig.11 gives wrong ground state energy of helium, when you calculate it.
Old helium gives the total energy of -83.33 eV, which is a little lower than the actual value of -79.005 eV (= 1st + 2nd ionization energy of this ).
(Fig.11) Actual Helium must avoid "destructive interference".
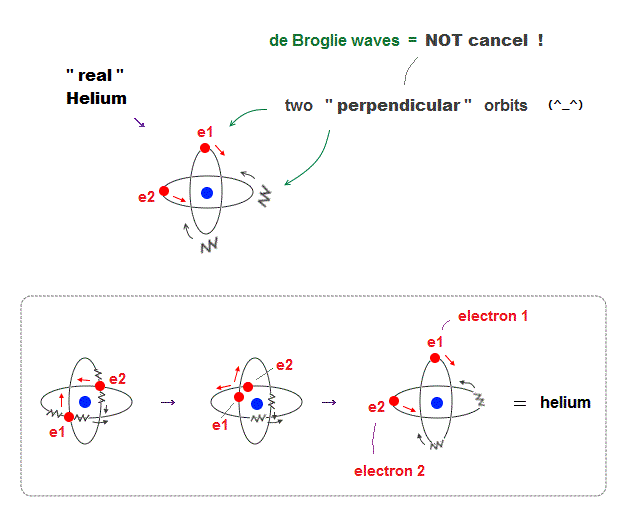
If two 1 × de Broglie wavelength orbits are in the same plane in old Bohr's helium model, their opposite wave phases cause destructive interference and vanish.
To avoid vanishing de Broglie's wave, two electron orbits in actual helium must be perpendicular to each other. Each orbit is one-de Broglie wavelength.
If the two orbits are perpendicular to each other, their wave phases are independent from each other and can be stable, not canceling each other.
This helium model considering actual de Broglie wave interference just agrees with experimental results of all atoms !
(Fig.12) Crossing perpendicularly avoids destructive interference
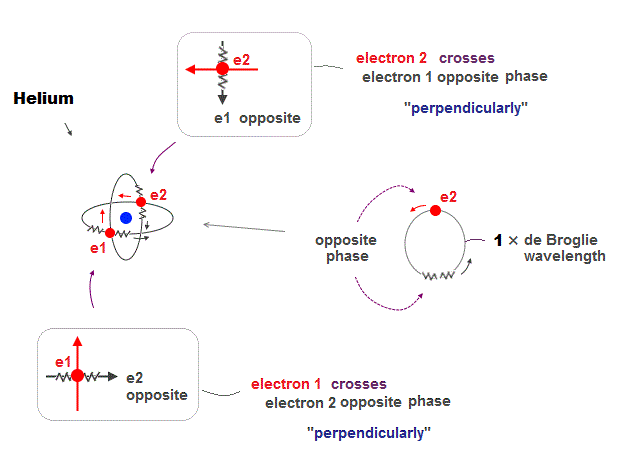
Helium consists of two electron orbits of 1 × de Broglie wavelength. Opposite wave phases inside one wavelength cancel each other by destructive interference.
To avoid this, Helium two orbits cross each other "perpendicularly". Its cancellation causes no magnetic field as seen in actual Helium.
(Fig.13) Two orbits of H2 molecule avoid destructive wave interference
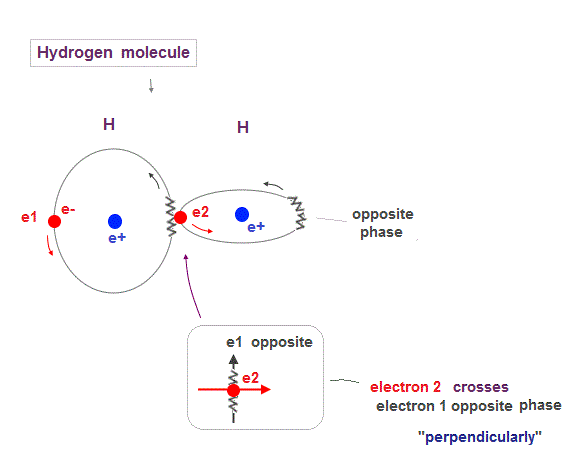
Like Helium atom, Hydrogen molecule (= H2 ) consists of two orbits of 1 × de Broglie wavelength.
So to avoid destructive interference, these two H2 orbits must cross each other "perpendicularly".
(Fig.14) 1 and 3 H "parallel" orbits cancel each other in H2 molecule
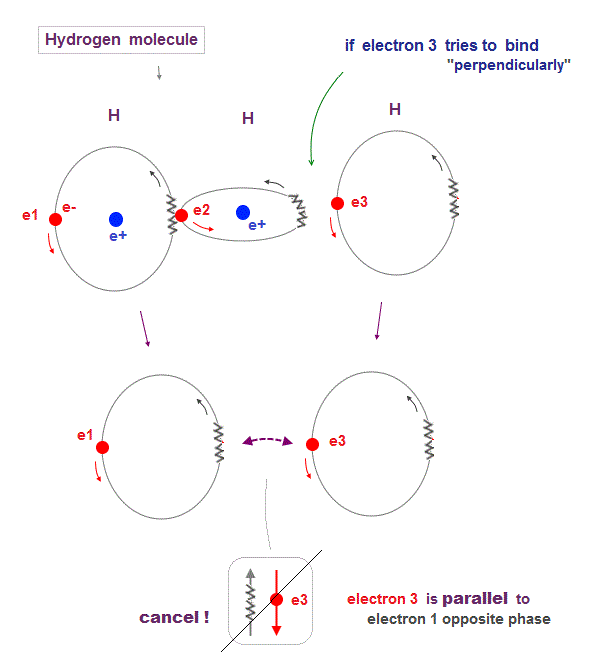
Hydrogen molecule (= H2 ) contains only two orbits at the maximum. Why three H orbits cannot form stable H3 molecule ?
When the 3rd hydrogen orbit tries to bind to the existing H2 molecule, orbits of 1st and 3rd must be parallel to and cancel each other out.
This is the reason why 1 × de Broglie wavelength orbit cannot make H3 (= three hydrogens ) molecule.
(Fig.15) 2 × de Broglie wavelength orbits. Each is a pair of opposite phases.
One wavelength consists of a pair of "crest" (= + ) and "trough" (= - ) irrespective of transverse and longitudinal waves.
Here we suppose "+" phase contains an electron itself, and "-" phase is compressed by the electron's movement, --- which is " de Broglie wave ".
2 × ( 1 × ) de Broglie wavelength orbit contains two ( one ) pairs of ±opposite phases and two ( one ) midpoint lines.
These "opposite" wave phases cancel each other by destructive interference.
To avoid it, two orbits must cross perpendicularly in all atoms.
(Fig.16) 2 × de Broglie wavelenght orbits contain "free" electrons
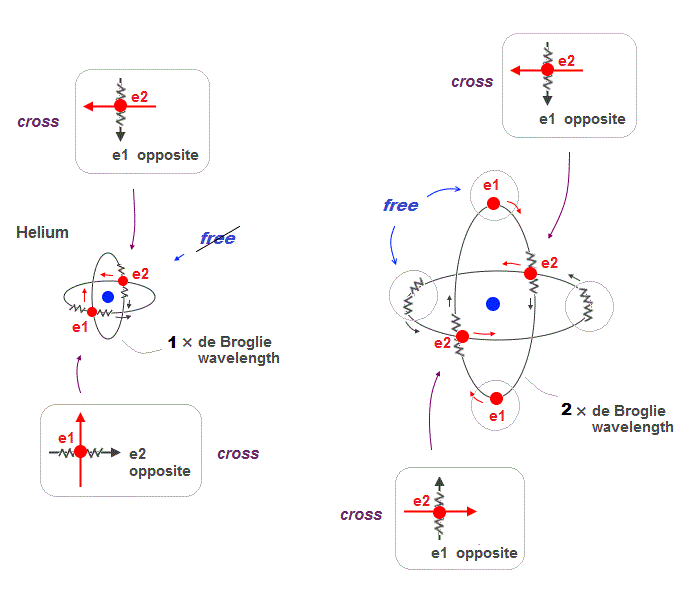
Helium two 1 × de Broglie wavelength orbits always cross their opposite (anti) wave phases at right angle.
On the other hand, when two 2 × de Broglie wavelength orbits cross each other, they contain "free electrons" and "free opposite phases" which aren't crossing.
So there is still a room for more orbits in 2 × de Broglie wavelength.
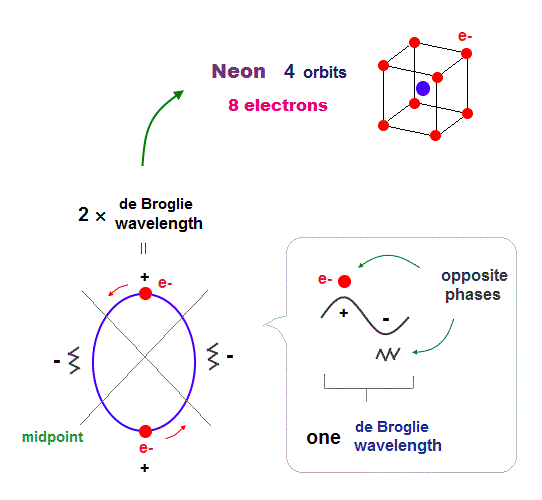
(Fig.17) All opposite wave phases just cross each other in Neon
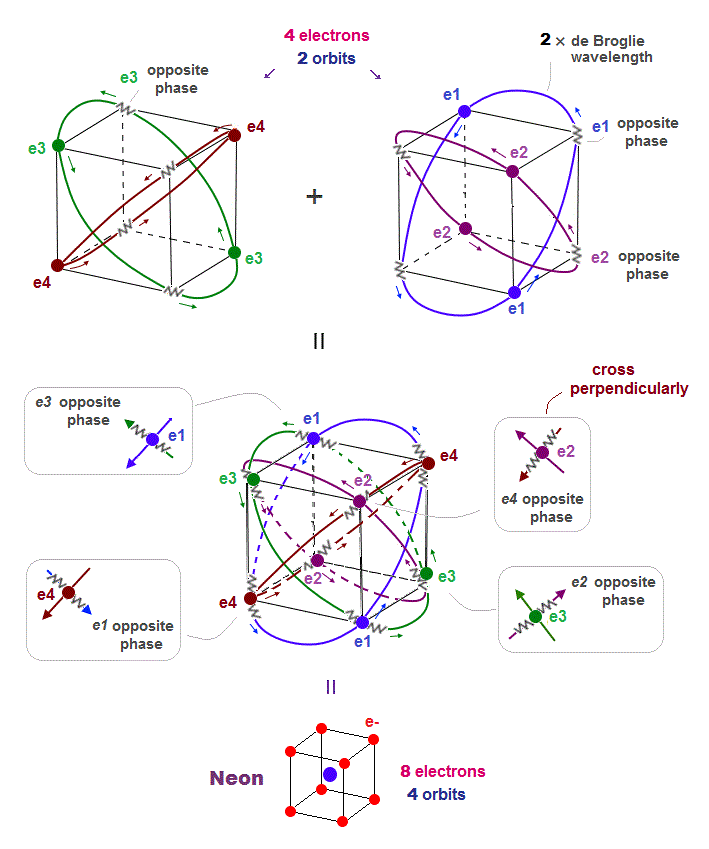
Neon contains eight valence electrons. Neon belongs to the 2nd line in periodic table, meaning its orbit is 2 × de Broglie wavelength.
When just two 2 × de Broglie wavelenght orbits cross each other (= Fig.17 upper ), some electrons are free from their opposite wave phases.
With four orbits, all electrons and their opposite wave phases cross each other, forming stable noble gas Neon with no more room.
(Fig.18) Orbits of Neon cross each other "perpendicularly".
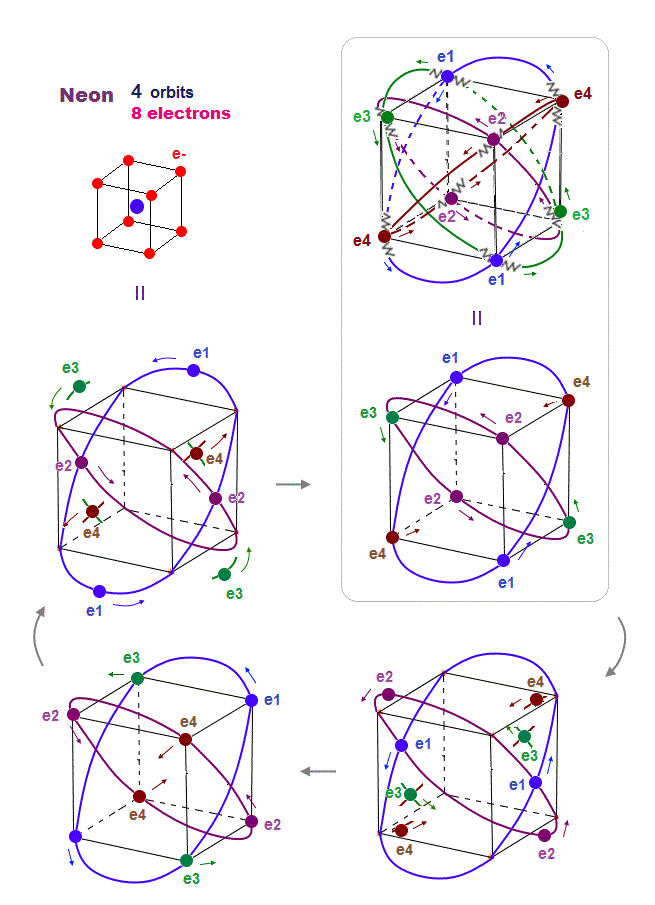
As shown on this page, we can show the appropriate new Neon model, in which orbits can cross each other "perpendicularly".
"Perpendicular" crossing means they can avoid "destructive" interference. Neon consists of four 2 × de Broglie wavelength orbits ( total 4 × 2 = 8 electrons )
(Fig.19) Carbon (= C ) is 4 electrons and "holes" in 4 orbits.
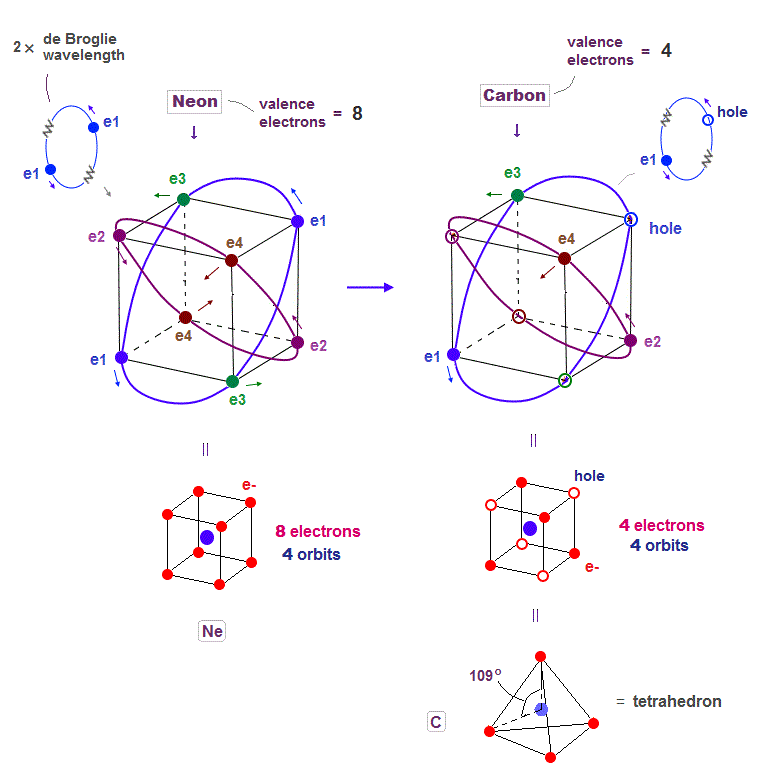
When each 2 × de Broglie wavelength orbit includes one electron and one hole, it generates four "holes". This is carbon (= C ) atom.
Carbon consisting of four valence electrons form tetrahedral structure with bond angle 109o.
(Fig.20) Hydrogen electron can enter "hole" of carbon
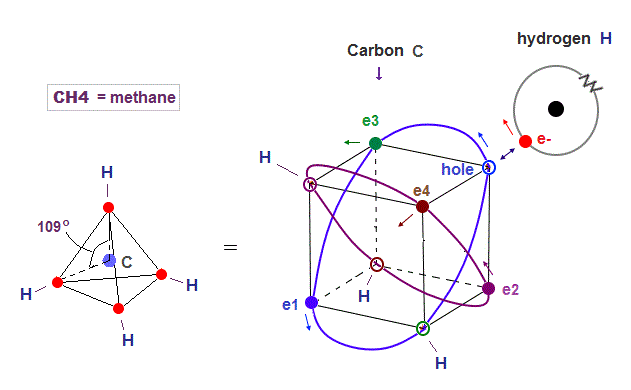
Carbon atom consists of four 2 × de Broglie wavelength orbits with a pair of electron and hole.
So electrons of other Hydrogen atoms can enter these holes and form C-H bond in methane (= CH4 ).
Hydrogen electron uses the hole of exisiting carbon orbit, so NO destructive interference happen like H3 molecule.
(Fig.21) "Three holes" in nitrogen form NH3 molecular bond
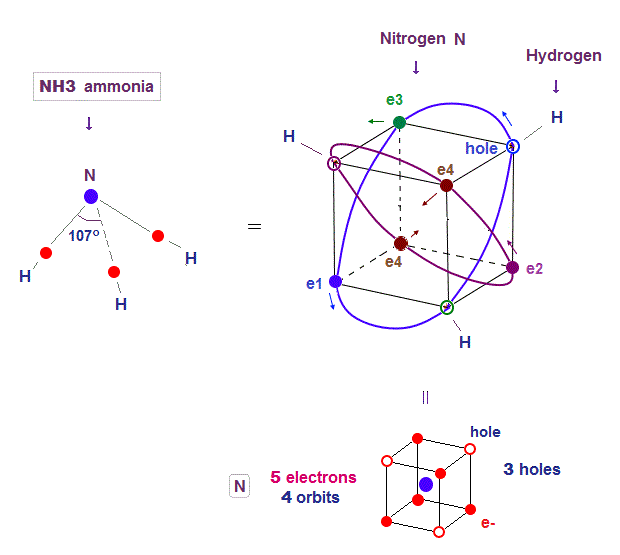
H-N-H angle (= 107o ) of ammonia (= NH3 ) is very close to 109o of tetrahedral carbon.
Notrogen (= N ) consists of 5 valence electrons and 3 holes in four 2 × de Broglie wavelength orbits.
Four 2 × de Broglie wavelength means even this nitrogen structure must be close to tetrahedron like carbon.
Due to the asymetrical number "five", tetrahedral structure is a little distorted by Coulomb repulsion in nitrogen.
So its NH3 bond angle 107o is slightly smaller than pure tetrahedral 109o
(Fig.22) Two holes in oxygen form H2O molecular bond
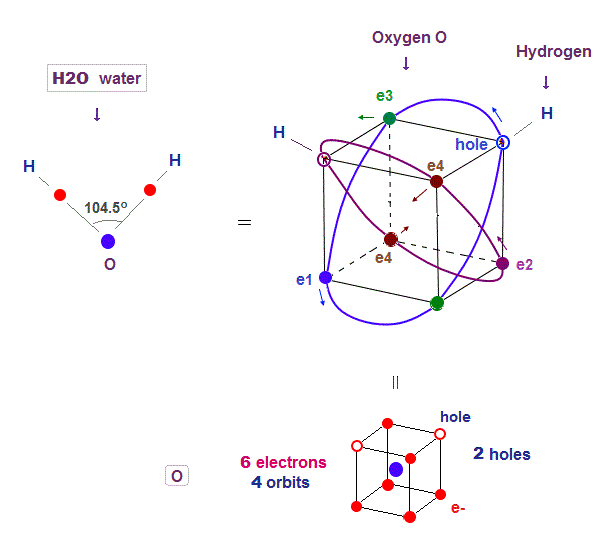
Four 2 × de Broglie wavelength means even this oxygen structure must be close to tetrahedron like carbon.
Due to the asymetrical number "six", tetrahedral structure is a little distorted by Coulomb repulsion also in oxygen.
So its H2O bond angle 104.5o is slightly smaller than pure tetrahedral 109o
(Fig.23) Six oxygen valence electrons closer to tetrahedron.

If we consider only Coulomb repulsion among six oxygen valence electrons, they form octahedral structure, so H2O bond angle is close to 90 degree. But is isn't.
This is due to electron's "de Broglie wave interference". In 2 × de Broglie wavelength orbit, there is almost no room for distorting tetrahedral structure.
(Fig.24) Longer Sulfur orbit can be close to octahedron
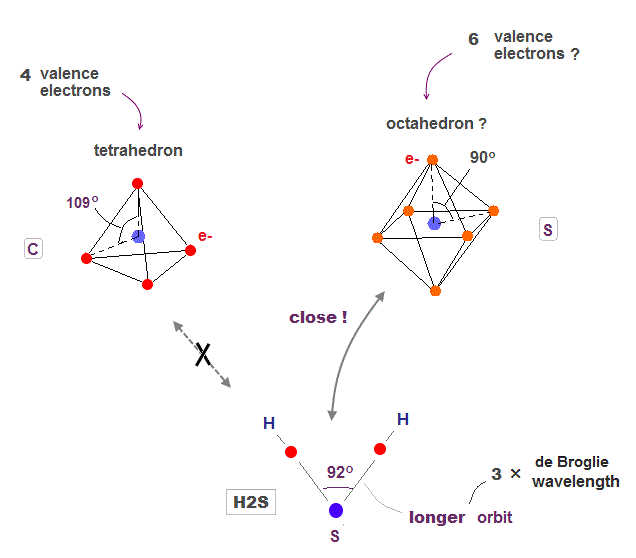
Sulfur also contains six valence electrons, and its bond angle (= H2S ) is closer to right angle of octahedron.
Because each orbit of sulfur is 3 × de Broglie wavelength, longer than oxygen. So there is a room enough to form octahedron obeying Coulomb repulsion.
As shown in Argon, the 3 × de Broglie wavelength orbit includes more "holes" binding to outer hydrogen. So two outer hydrogens can approach each other at 90o bond angle.
In 2 × de Broglie wavelenght orbit Neon, we cannot remove only both two electrons of the same one orbit ( ex. e1-e1 electrons ).
(Fig.25) ↓ s and p orbitals just show "90o" in oxygen

Solving Schrodinger equation gives simple electron orbitals (= s, p .. ) with only right angle (= 90o ).
So basically, quantum mechanics cannot give clear reason why H2O angle in water is NOT 90 degree.
Though physicists try to find a lame excuse that only oxygen ( not sulfur ) can form different mixed sp orbital. This is too good to be true, and NOT science.

2016/9/9 updated. Feel free to link to this site.