When we partially differentiate the (covariant) vector A with respect to x, and do coordinate transformation (= generalized Lorentz transformation )
(Eq.1)
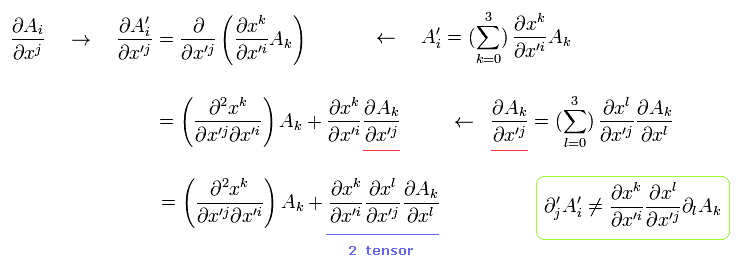
Top page (quantum mechanics is wrong. ← 6/30/2024 )
General relativity is really correct ?? ← 6/15/2024
In fact, Einstein special and general relativity includes fatal paradoxes, so false.
If you have not read the first half of this page ( General and special relativity ), read it first.
When we partially differentiate the (covariant) vector A with respect to x, and do coordinate transformation (= generalized Lorentz transformation )
(Eq.1)
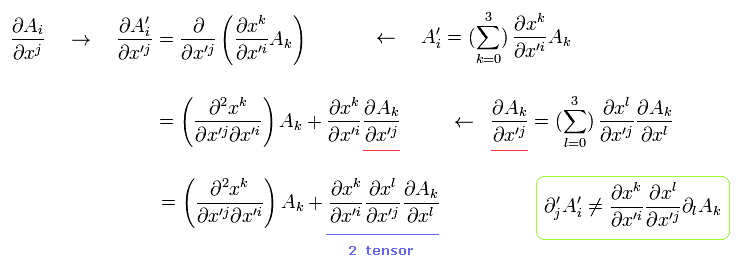
Eq.1 transformation is different from Minkowski spacetime of
(Eq.2)
Because general coordinate transformation (= "generalized" Lorentz transformation ) is twice differentiable ( first term of right side in Eq.1 ).
Only the second term of Eq.1 means the 2-rank tensor change in the partial derivative of the vector A.
If the partial differential operator is not covariant four-vector, the calculation becomes very troublesome.
So we need to define the new differentiation (= covariant derivative ) in Riemannian space, as follows,
(Eq.3)
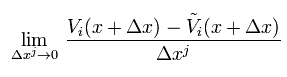
If the numerator includes only x+Δx ( not x ), the first term of right side of Eq.1 needs NOT to be considered.
So derivative becomes tensor, which is explained later.
The definitions of Eq.3 and Eq.4 are artificial things to match the relativistic covariance.
Tilde-V of Eq.3 means parallel transpoted vector, which is defined as
(Eq.4)
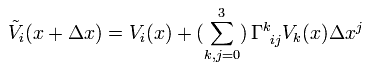
where the coefficient Γ is called Christoffel symbols (or coefficients of affine connection ).
And the change of V(x) is supposed to be in proportion to the original V(x) and Δ x.
We suppose Eq.4 satisfies the constant scalar of
(Eq.5)
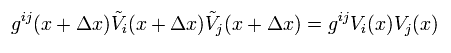
Eq.5 is equal to
(Eq.5-2)
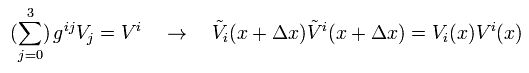
Do you understand the meaning of paralled transported tilde-V vector of Eq.4 ?
The metric tensor g(x) changes depending on the position, because the gravity is different in different places.
Eq.5 means scalar length is invariant even at the different position x.
Of course, the scalar length is a common value both in Riemann and Minkowski spacetimes.
As shown on this page, the energy (E) and momentum (=p) scalar length of the free particle is related to the rest mass energy, as follows,
( Of cource, this rest mass energy is invariant under the coordinate transformation. )
(Eq.6)
But if some external force such as the electromagnetic force (potential) acts on the free particle, this scalar length of Eq.6 changes.
So the constant scalar length of Eq.6 means a free particle except for the gravity.
Paparell transfort means the change of the vector ONLY by the gravity (= other forces such as Coulomb force don't exist ).
Here we get the parallel transport of contravariant vector V of
(Eq.6-2)
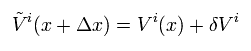
Substituting Eq.6-2 and Eq.4 into Eq.5-2,
(Eq.6-3)
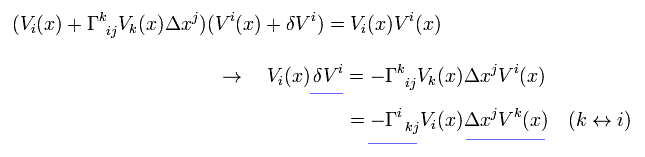
where neglecting second-order infinitesimal terms.
As a result, parallel transport of contravariant vector is
(Eq.6-4)
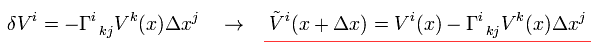
An expansion of g(x+Δ) is
(Eq.7)
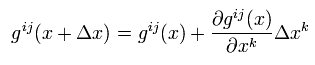
Substituting Eq.4 and Eq.7 into Eq.5,
(Eq.8)
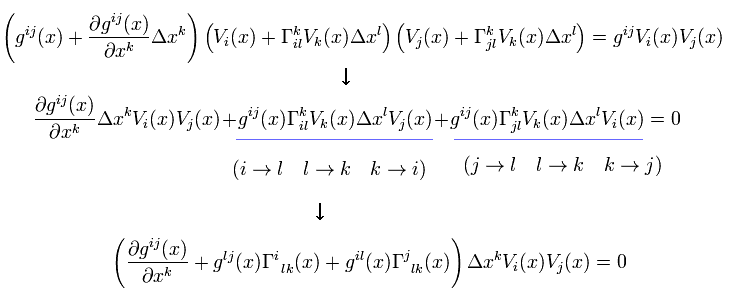
where we neglect second-order terms of Δ x.
( We can change symbols of two indices over which we contract. ex. i i → k k )
Eq.8 holds for random Δ x and V. So we get the relation of
(Eq.9)
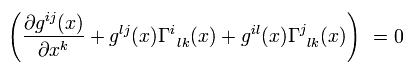
We suppose the Christoffel symbol satisfies
(Eq.10)
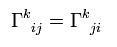
Here we prove the next relation of
(Eq.11)
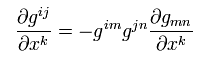
Metric tensor satisfies
(Eq.12)
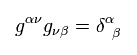
From Eq.12
(Eq.13)
Neglecting second order infinitesimals of δg
(Eq.14)
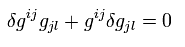
Multiplying Eq.14 by grl,
(Eq.15)
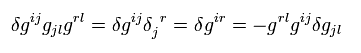
Changing the indices, as follows,
(Eq.16)
we can prove Eq.11.
The second term of Eq.9 is
(Eq.17)
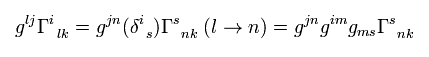
And the third term of Eq.9 is
(Eq.18)
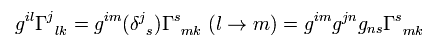
Substituting Eq.11, Eq.17 and Eq.18 into Eq.9,
(Eq.19)
Here we define
(Eq.20)
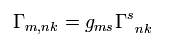
Eq.19 is
(Eq.21)
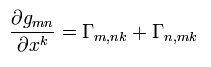
Permuting the indices of Eq.21,
(Eq.22)
In the same way,
(Eq.23)
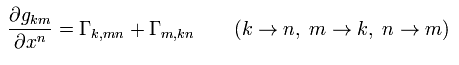
( Eq.21 + Eq.22 - Eq.23 )/2 is
(Eq.24)
where we use Eq.10.
Using the relation of
(Eq.25)
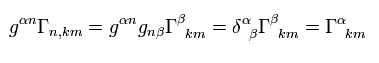
Eq.24 becomes
(Eq.26)
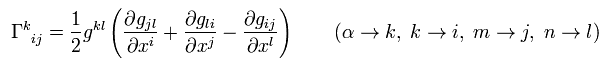
So we can express Christoffel symbol using the metric tensor g.
As I said, these Christoffel symbols and the metric tensors are related to the gravity at that point.
As you see this page, there are many artificial definitions in the general relativity to fit in with covariance.
Of course, basically the equations of general relativity can NOT be solved.
Only from approximations and very tiny effects, it is very difficult to believe the general relativity.
( We should consider much bigger contradictions such as dark matter rather than the very tiny effects. )
As I said above, tilde Vi (x+Δ) needs to be a covariant vector to make the calculation easy.
Under the general coordinate transformation (= "generalized" Lorentz transformation ), this tilde V changes like
(Eq.27)
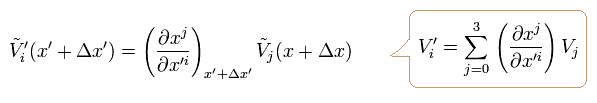
Here we use the relation of
(Eq.28)
Substituting Eq.4 and Eq.28 into Eq.27,
(Eq.29)
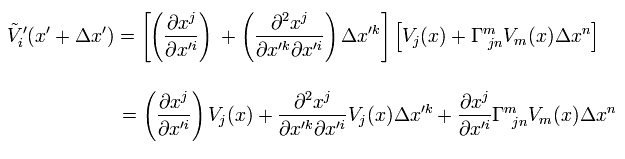
where we neglect second order terms of Δ x.
Using the relation of
(Eq.30)
Eq.29 becomes
(Eq.31)
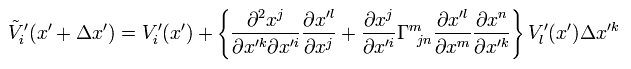
Like Eq.4,
(Eq.32)
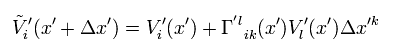
Considering Eq.31 is equal to Eq.32, we obtain
(Eq.33)
As you notice, if only the second term of Eq.33 is left, this Christoffel symbol changes as mixed tensor of 3rd rank.
This means Christoffel symbol is not tensor (= not covariant or contravariant vectors )
And Christofell symbol needs to change as Eq.33 under general coordinate transformation to make tilde V of Eq.4 a covariant vector.
We define Eq.3 as a covariant derivative, as follows,
(Eq.34)
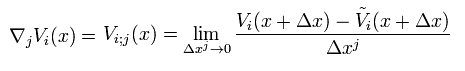
As I said in Eq.5 and Eq.6, if only gravity exists, this Eq.34 becomes zero.
So Eq.34 means vector's change under the forces other than gravity in Riemannian spacetime.
Substituting Eq.4 into Eq.34,
(Eq.35)
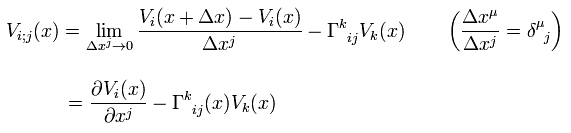
Eq.35 is called covariant derivative of a covariant vector Vi(x).
From Eq.6-4, the covariant derivative of a contravariant vector Vi(x) is
(Eq.35-2)
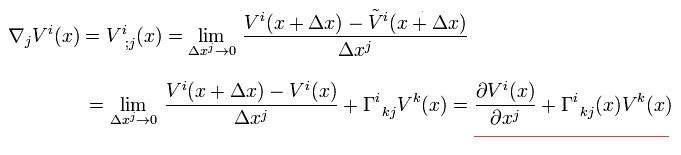
Eq.35 changes as a covariant tensor of 2nd rank.
Because we defined Eq.27 to make tilde V a covariant vector.
( Of course, V and Δ x are vectors from the beginning. )
And different from the usual differentiation, vectors V(x + Δx) and "tilde V(x + Δx)" in the numerator of the covariant derivative of Eq.34 are at the same position (= x + Δx ).
So the covariant derivative doesn't need to include the change of the coordinate transoformation by the position ( x → x+Δx ), thus the first term of Eq.1 doesn't appear in the covariant derivative, which means tensor.
Here we prove Eq.35 is 2nd rank covariant tensor by calculation.
Using Eq.1 and Eq.33, Eq.35 transforms under coordinate transformation as
(Eq.35-3)
where we use
Exchanging "n" and " l ", and "n" is changed into "k" in the last term.
Next we prove two kinds of vectors A and B satisfy
(Eq.36)
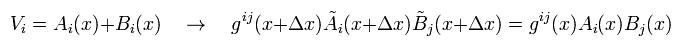
Substituting V=A+B of Eq.36 into Eq.5,
(Eq.37)
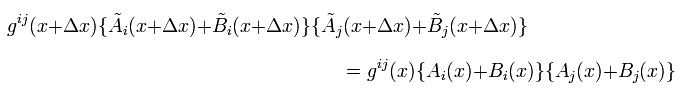
Using the relations of
(Eq.38)
we can prove Eq.36.
Using the relation of
(Eq.39)
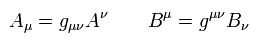
Eq.36 can be expressed as
(Eq.40)
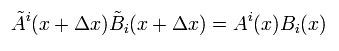
( Definition: gij = gji )
As I said in Eq.6-4, the contravariant vector changes under parallel transport as
(Eq.44)
So the covariant derivative of contravariant vector A is
(Eq.44')
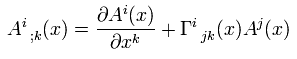
Next we think about mixed tensor ( contravariant A + covariant B ) under parallel transport.
(Eq.45)
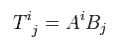
Using Eq.4 and Eq.44, Eq.45 changes as
(Eq.46)
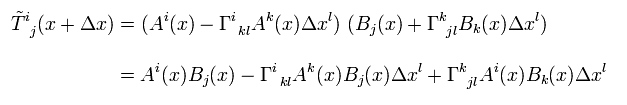
where the second order term of Δx is neglected.
Using the relations of
(Eq.47)
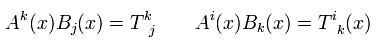
Eq.46 is
(Eq.48)
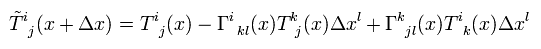
As a result, mixed tensor changes as ( Eq.4 + Eq.44 ).
And the covariant derivative of the tensor is
(Eq.49)
(Eq.50)
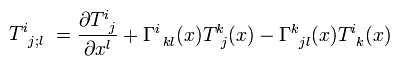
Using Eq.50, the covariant derivative of the metric tensor g (= covariant × covariant ) is
(Eq.51)
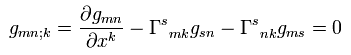
From Eq.19, Eq.51 is zero.
Covariant derivative of contravariant metric tensor gij is zero, too ( using Eq.12 and Eq.51 ).
(Eq.52)
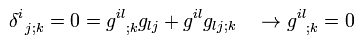
Next we do second-order covariant differentiation ( with respect to Δxi and Δxj ).
The first line Eq.E.53 is the covariant derivative of Am; i with respect to j (see also Eq.51, Eq.50 and Eq.35 ).
(Eq.53)
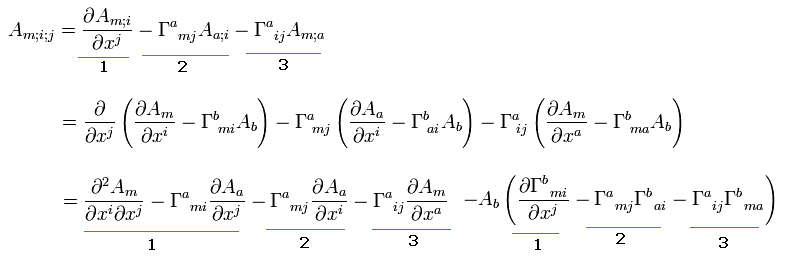
We use Eq.35 or Eq.50 twice and change indices properly in Eq.53.
Each number ( 1, 2, or 3 ) mean the same source term.
Changing the order of covariant differentiation ( i and j of Eq.53 ) and subtracting one from another,
(Eq.54)
where only the fifth and sixth terms of Eq.53 (last line) are left.
Eq.54 can be expressed as
(Eq.55)
This 4th rank tensor R is called Riemann's curvature tensor.
If all components of this Riemann curvature tensor R are zero, differentiations are exchangeable, which case corresponds to Minkowski spacetime.
When A of Eq.55 is contravariant vector Vm,
(Eq.56)
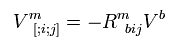
Here we use Eq.44' and its covariant derivative and do calculation like Eq.53.
Covariant 4th rank tensor form of R is metric tensor g × Eq.55, as follows,
(Eq.57)
If we move into local inertial frame (= local Minkowski spacetime) at point x ( by coordinate transformation ), Christoffel symbols Γ of Eq.24 and Eq.26 is zero.( g = η, Γ = 0 at point x ).
So the first order derivative of g (= η = g at x ) and Γ are zero at the position x in the local inertial frame.
But the second order derivative of g may not be zero.
In this case (= local Minkowski ), Rieman curvature tensor of Eq.57 is ( using Eq.55 and Eq.26 )
(Eq.58)
In the second line of Eq.58, two terms of red line cancel each other.
(And the first-order derivative of g is zero. )
And the second order derivative of g is left.
From Eq.58, we can prove the relations of
(Eq.59)
And then we go back to Riemann spacetime by the coordinate transformation,
(Eq.60)
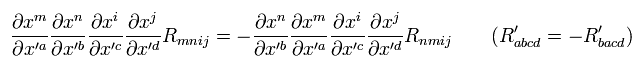
So Eq.60 means Eq.59 is always satisfied in any Riemann spacetime, because R is tensor.
Contracting (= summing from 0 to 3 ) the first and third indices (= i i ) of Riemann curvature tensor of Eq.55,
(Eq.61)
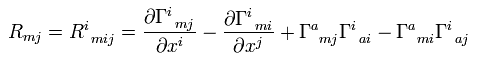
Eq.61 is called Ricci tensor.
Ricci tensor is symmetric like Rij = Rji , as follows,
(Eq.62)
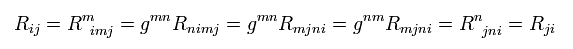
where we use Eq.59.
Furthermore, contracting Ricci tensor, we get
(Eq.63)
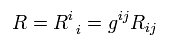
This is called scalar curvature.
Next we prove the relation of
(Eq.64)
Eq.64 is called Bianchi identity.
Eq.64 is a tensor of 5th rank, so like Eq58 - Eq.60, if we can prove Eq.64 in local inertial frames, Eq.64 is always satisfied in the generalized Riemann spacetime.
In local inertial frames, Christoffel symbol (= the first derivative of g ) is locally zero.
( The second derivative of g may not be zero. )
So from Eq,55,
(Eq.65)
Summing three equations of Eq.65, the right side becomes zero, which is equal to Eq.64.
Multiplying Eq.64 by the metric tensor g,
(Eq.66)
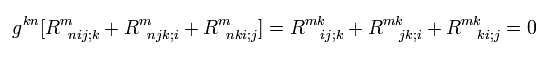
As shown in Eq.51 and Eq.52, the covariant derivative of the metric tensor g is zero.
So we can treat g as a constant and put it into the covariant derivative.
And changing j to m and contracting over m in Eq.66,
(Eq.67)
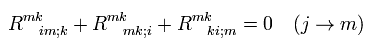
The second term of Eq.67 is the covariant derivative of scalar curvature (= Eq.63), and the first and third terms are the same, as follows ( changing indices ),
(Eq.68)
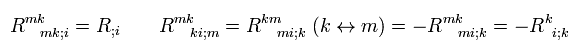where we use Eq.59.
From Eq.68, Eq.67 is
(Eq.69)
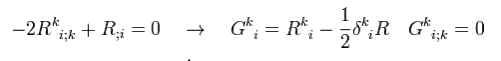This G is called Einstein tensor.
As you notice, the relation of Eq.69 is similar to the energy momentum tensors such as the electromagnetic fields.
Covariant Einstein tensor of 2nd rank is
(Eq.70)
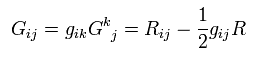
The divergence of the contravariant Einstein tensor of 2nd rank is zero, too.
(Eq.71)
As I said, the metric tensor g can be treated as a constant in the covariant derivative.
Contracting Einstein tensor of Eq.69,
(Eq.72)
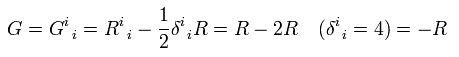
Inserting Eq.72 into Eq.70,
(Eq.73)
Ricci tensor can be expressed using Einstein tensor.
A determinant of the metric tensor matrix g can be expressed using its cofactors Y (= cofactor expansion ),
(Eq.74)
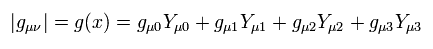
where
(Eq.74-2)
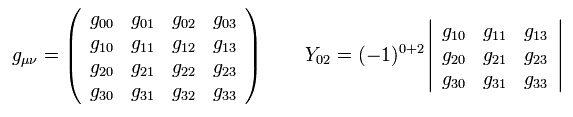
where μ of Y is only a symbol, which should not be contracted over.
An inverse matrix of g is
(Eq.75)
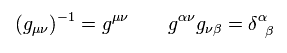
Partially differentiating Eq.74, and multiplying Eq.74 by Eq.75 to Kronecker's δ, we get
(Eq.76)
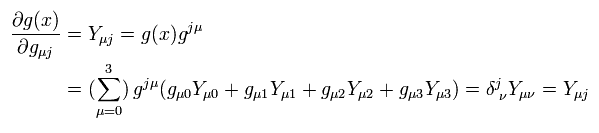
From Eq.76, we get the important formula of
(Eq.77)
2012/4/9 updated. Feel free to link to this site.