トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは実在しない
我々の新しいボーア模型によって、ヘリウム原子の基底状態エネルギーの計算で、量子力学的な変分法よりも正確な結果をだすのに成功した。(トップページ参照のこと)。
この成功した新ボーア模型では、ヘリウム原子 (He) の2つの電子は、ちょうど1ド・ブロイ波長の互いに垂直な軌道上を運動している。
また、この新しい原子模型は、パウリの排他原理の現象も正確に説明できる。なぜなら、この新しいボーアの2電子原子には、3つめの電子が入りこむスペースがないからだ。
驚くべきことに、この新しいボーアのヘリウム構造は、他の2電子原子(イオン)である、リチウムイオン (Li+)、ベリリウムイオン (Be2+)、ホウ素イオン (B3+)、炭素イオン (C4+) にも正確にあてはめることができた。
(このページを参照のこと。)
さらに、3電子原子である、リチウム原子 (Li) のイオン化(基底状態の)エネルギーも、近似的なボーア模型の”2S”軌道を使用して、計算することができた。(このページも参照のこと。)
我々は、酸素のページ に示したように、酸素原子 (O) の6つの電子の運動を実際に画面上に視覚化するのに成功した。
このセクションは、その酸素のページと同じ内容なので、すでにそちらのページを読んだ人は、次のセクション (すべての軌道はやがて平衡状態で安定するようになるのか ?) に進まれるとよい。
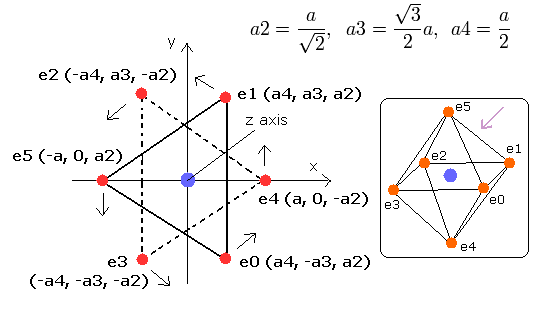
ここでは、酸素原子の6つの価電子が正八面体状に配置されているとする。
(6つの頂点(=6つの価電子)をもつ対称な正多面体は正八面体であるから。)
中性の酸素原子には8つの電子がある。そのうち2つの1S電子は核にとても近づいている。
つまり、近似的に我々は6つの電子が +6e の中心核 (+8e - 2e = +6e) の周囲を運動していると仮定できる。
また、この6つの外殻電子は互いに避け合いながら、この核の周囲を対称的に運動していると考えられる。
正多面体の中で、正八面体が6つの頂点(=6つの外殻電子)を持つ。
そこで我々は、酸素原子の6つの価電子が、Fig.1 に示すように正八面体状に配置されていると仮定できる。
Fig. 1. 推定される酸素原子 (正八面体). 原子核=(0,0,0)

ここでは、次のサンプル JAVA プログラム (version 1.5 (5.0)) を使って画面上に酸素原子の電子の運動を視覚化してみることにする。
このプログラムは少し長いので、中に示すソースプログラムをコピーして、テキストエディタ(メモ帳など)にそのまま貼り付けて、コンパイルすれば簡単に実行できる。
このプログラムの class file name は oxygen2 なので、このデキストエディタを "oxygen2.java" のファイル名で保存してコンパイルしてほしい。
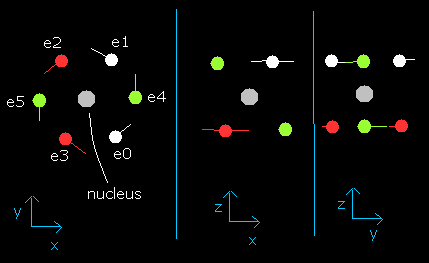
このプログラムでは、酸素原子核は、灰色の円 (Fig. 2 参照)で表示している。
また6つの電子は、e0, e1 は白、e2, e3 は赤、e4, e5 は緑色の円でそれぞれ示してある。
x, y, z 軸は Fig.1 に示す軸である。
左、真ん中、右の図はそれぞれ、x-y, x-z, y-z 平面を表している。
また、各電子の速度ベクトルは線で示してある。
Fig. 2. プログラム中の酸素原子核と6つの価電子 (wn=0)
テキストボックス内の電子の各座標 (+X (MM), +Y (MM), +Z (MM)) は、この原子核からの”相対的な”位置座標を示している。
ここでは次のような新しい単位を用いている。
"nuc (MM)" は、核と各電子の間の距離を意味している。
"VX: VY: VZ" は電子の初速度の各成分の比を示している。
つまり、(VX: VY; VZ)=(100:100;0) は、(VX: VY: VZ) = (10:10:0) と同じ意味である。
スクロールバー (0.1 -- 2.0) の中から、ド・ブロイ波の数 (=wn) を選んで、"orbit" ボタンをクリックすると、このプログラムは、軌道に含まれるド・ブロイ波の数が wn になるまで電子軌道計算を続ける。
詳細な計算方法については、トップページを参照のこと。
微小時間 (1 SS) ごとに、6つの電子と核の間のクーロン力を計算し、その結果を基に各速度ベクトルを変化させていく。
また、各電子につき、微小区間に含まれるド・ブロイ波の数も計算していく。
(このプログラムでは、6つの価電子の全エネルギーは、第1〜6のイオン化エネルギーの合計である、-433.103 eV としている。)
このプログラムは、テキストボックスと模式図としての両方に、各電子の最後の座標と速度ベクトルの結果を表示する。
それから、"retur" ボタンをクリックすると、すべての電子は、また最初のスタートラインの状態に戻ることができる。
また、"radiu" ボタンの隣のテキストボックスに a (MM) (Fig.1参照) の値を入力して "radiu" ボタンをクリックすれば、Fig.1 に示すように、6つの電子の正八面体の大きさ(半径)が変化する。
最初に、a (MM) として、3820 の値を入力して "radiu" ボタンをクリックしてみる。
(この場合は、Fig.1 の a の値は 3820 (MM) となり、原子核と各電子の最初の距離 (=nuc) は 4678 MM となる。
次に、スクロールバーの中から、ド・ブロイ波の数 (wn) として 0.5 を選んで、"orbit" ボタンをクリックしてみると、計算が開始して、次のようなイメージ結果が表示される。
Fig. 3. wn = 0.5 における酸素原子の電子
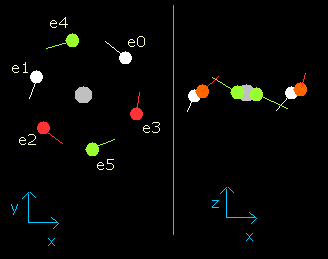
電子が、0.5 ド・ブロイ波長分の軌道を進んだとき (wn=0.5)、酸素の6つの価電子はすべて、x-y 平面近くに位置しており (Fig. 3 右図)、つまり原子核が外にさらけ出されている。
また、この地点 (wn=0.5) では、原子核と電子の距離は約 4204 MM である。
次に、"retur" ボタンをクリックして、wn=0 の最初の状態に戻ろう。
それから、スクロールバーの中で 0.9 の値をド・ブロイ波の数 (wn) として選び、また"orbit" ボタンをクリックする。(Fig.4)
Fig. 4. wn = 0.9 における酸素原子の電子
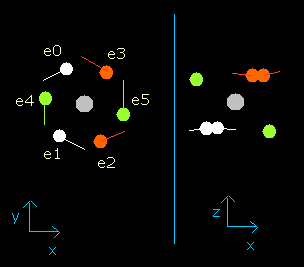
このイメージ結果は、電子が 0.9 ド・ブロイ波長分の軌道を進んだとき、酸素原子の6つすべての価電子は、その最初の位置から正反対のところに移動していることを示している。
wn=0.9 の地点では、原子核と電子の間の距離は最も短く ( = 3801 MM) なる。
また、"retur" ボタンを押して、今度は 1.9 の値を選択し、"orbit" ボタンをクリックしてみる。
結果は、Fig.5 に示すようになる。
Fig. 5. wn = 1.9 における酸素原子の電子 (=ほぼ wn=0.0 と同じ。)
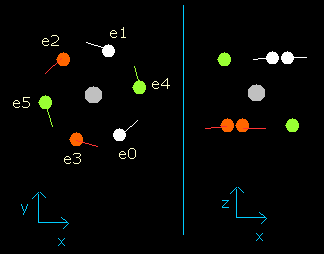
この結果は、6つすべての電子が、1.9 (ほぼ 2.0) ド・ブロイ波長分の軌道を進んだときに元の位置に戻ることを証明している。
(おそらく、これらの軌道は少しだけ歳差運動や揺れ運動をしていると思われる。)
上のプログラムでは、中心の仮の正電荷をちょうど +6.0e ( = +8e (原子核) -2e (2つの 1S 電子) = +6e) としている。
しかし、酸素のページ で示したように、2つの 1S 電子は、約 700 MM ほど、+8e の酸素原子核から離れている。(それらは、核にくっついているわけではない。)
そのため、6つの外殻電子に影響を与える"実質的な中心電荷"は、おそらく +6.0e よりも少し大きくなるだろう。
そこで、ここでは、中心の仮の正電荷を +6.0e のかわりに +6.3e として、もう一度軌道計算をしてみることにする。
サンプル JAVA プログラム (中心の仮電荷 +6.3e )
このサンプルプログラムは、中心の仮の正電荷を除いて上に述べたプログラムと同じである。
このプログラムでは、電子の進んだ軌道の長さが ちょうど 2.0 ド・ブロイ波長分になったとき、酸素の6つの価電子すべてが 次に示すように、もとの位置に戻ることができる。
Fig. 5-2. wn = 0.0 と wn = 2.0 のときの酸素の価電子 (”実質的な”中心電荷 = +6.3e)
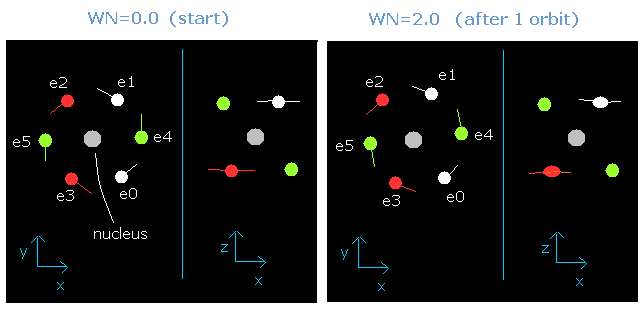
この結果はとても重要である。
6つの価電子の全エネルギーがある値 (=-433.103 eV) に決定すると、1軌道の平均の長さはだいたい一意的に決まる。
(このことは、全エネルギーの値を決めると、平均の軌道長、すなわち1軌道に含まれるド・ブロイ波の数が”自動的に”決まることを意味している。)
そして、この波の数が、中性の酸素原子の場合は 2.0 になることが証明された。
(つまり、この結果は、酸素原子の6つの価電子は、 2.0 ド・ブロイ波長の軌道上を運動していることを示している。)
中心の正電荷 (Z) がちょうど +6.0e (=+8e-2e) としたとき、1軌道に含まれるド・ブロイ波の数 (wn) は、 1.9 になる。
しかし、実際は2つの 1S 電子は +8e の原子核にくっついていないので、この中心電荷 (Z) を +6.3e (+6e より少し大きく) と仮定すると、上に示したように、1軌道のド・ブロイ波がちょうど 2.0 になった。
ここでは、このことを ビリアル定理 (Virial theorem) を用いて証明してみることにする。
我々は、次に示すように酸素の6つの価電子が +Ze の中心電荷の周囲に”八面体状に”配置されていると仮定する。
Fig. 5-3. 酸素原子の価電子 ("有効" 中心電荷 = +Ze)
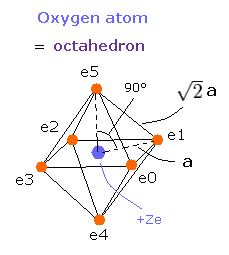
Fig. 5-3 では、電子と中心の正電荷の距離を a とする。
ビリアル定理によれば、”平均の”全位置エネルギー (V) と運動エネルギー (T) は次の関係にある。
< V > = -2 × < T > , E = V + T
6つの価電子の全エネルギー (E) は、-433.103 eV なので、この位置エネルギー (V) は、2 × -433.103 = -866.206 eV となる。
Fig. 5-3 の模型を使って、電子ー核、 電子ー電子の間の電位を計算していくと、全位置エネルギー V ( 単位 eV --> J ) は次のように示せる。
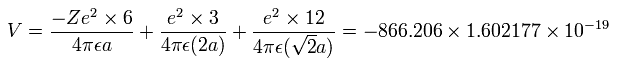
また、6つの電子の全運動エネルギー (T) は、433.103 (eV) である。
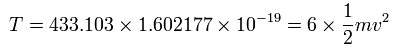
また、Fig.5-3 より、電子1つにはたらくクーロン力の合計 (F) は(核方向の力になるが)、次のようになる。
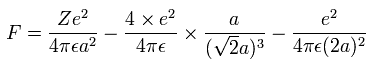
上の式の T 中の速度 (v) と、力 F の値を用いて、遠心力がこの力 (F) に等しいと仮定する。
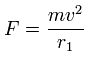
この r1 は、この関係式で初めて登場する 仮の半径である。
この r1 を用いて、次に示すように、1軌道に含まれる ド・ブロイ波の数 (wn) を計算することができる。
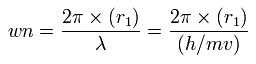
中心電荷 Z が +6.0 のとき、この wn は 1.88 (ほぼ 1.9) となる。
また、Z = +6.3 のとき、この wn は、ちょうど 2.01 になる。
つまり、我々はビリアル定理によって、このことを証明することができた。
もし、上のテキストボックス内の最初の座標や速度ベクトルの値を少し変えてから、"orbit" ボタンをクリックしてみる。
すると、少し値を変えただけで、例え6つの電子のエネルギーが同じ条件でも、6つの電子の対称性は壊れて、ばらばらに散ってしまう。
これは、それらが同じエネルギー状態でも、6つの電子は非対称にバラバラになってしまうことを意味するのだろうか?
答えは、電子軌道は、ゆくゆくは安定な平衡状態になる。
ここで、Fig. 6 に示す簡単な2電子原子モデルを使って、このことを説明しよう。
(これは、あくまで”近似的な”摸式例であり、実際の原子ではないことに注意。)
Fig. 6. 軌道は時間とともに”非対称に”なってしまうのか ?
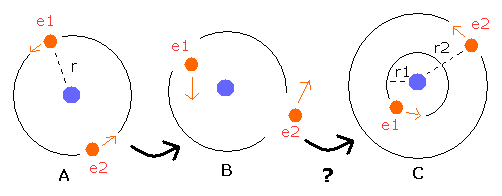
Fig.6-A では、2つの電子は、同じ半径 r の軌道上を”対称的に”運動している。
2つの電子は同じエネルギー (E= V + T) を持つと仮定する。
もし、Fig. 6-B に示すように最初の速度ベクトルの方向を "非対称"な方向に変化させると、これらの電子は、ゆくゆくは Fig.6-C に示すような非対称な軌道を運動するようになってしまうのだろうか?
基本的に、電子軌道半径が安定するしているとき、Eq. 1 に示すように、遠心力がクーロン力とつりあっている。
(Eq. 1.)
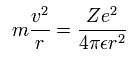
ここで、rは半径、m は電子質量、v は電子の速度、-e は電子の電荷である。
Z は、原子核と他の電子の影響を含めた、”有効”正電荷である。
各電子の全エネルギー E は、運動と位置エネルギーの合計である。(Eq.2)
Eq.1 を Eq.2 の運動エネルギー項に代入すると、結果は次のようになる。
(Eq. 2.)
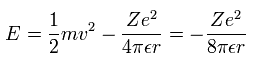
もし、電子1 (e1) が元の r (r1 < r) よりも小さな 半径 (r1) の軌道を運動しているとすると、電子2 (e2) は、もとの r よりも大きな半径 (r2) の軌道上を運動するようになる。
なぜなら、これらの電子のエネルギーの合計は変化しないからである。(Fig.6-C)
つまり、電子1 (e1) の視点からすると、電子1は電子2よりも内殻の軌道に入りこむため、”有効”正電荷 Z は、大きくなる。
Eq.2 によれば、もし、r が小さく、Z が大きくなると、電子1の全エネルギーは元のものよりも小さくなる。
(一方で、電子2の全エネルギーは元のものよりも大きくなる。)
この結果は、2つの電子が同じエネルギーを持つという最初の前提に矛盾する。
結果として、各電子のエネルギーが同じとき、すべての電子はゆくゆくは”対称的な”軌道上を安定して運動するようになる。
次に、水 (H2O) の視覚化に挑戦する。
水分子では、(H2O --> 2H + O ) の反応に必要な解離エネルギーは、9.6066 eV (926.9 kJ/mol) である。
つまり、平均の 1つのO-H 結合エネルギーは、9.6066/2 = 4.8033 eV である。
この結合エネルギーはそんなに大きくはない。すなわち、水素と酸素原子の各電子たちは、元の原子核につながったままであると考えられる。
H2O の全エネルギー は、-433.103 (O) - 2 × 13.606 (H) - 9.6066 (bond energy) = -469.92 eV.
である。
Fig. 7. 水分子 (H2O) 模型
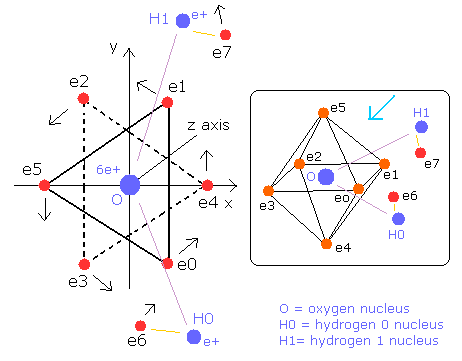
水の O-H 結合長は、9584 MM (= 0.9584 × 10-10 meter) である。
H-O-H 角は、104.45 ° で、90°(酸素原子の 電子0 - 核 - 電子1 の角)よりも大きい。
つまり、H-H 結合長は、15150 MM (= 1.5150 × 10-10 meter) となる。
ここでは、次のサンプル JAVA プログラム を使って、水分子の電子軌道を計算する。
水分子の構造は、非対称である、これは、酸素原子やメタン分子 (CH4) とは違う。
つまり、水分子の適切な平衡状態の電子軌道を見つけるのことは、はるかに難しい。
この困難な原因は2つある。
もし、少しでも、不適切な(非平衡状態の)初期条件を設定すると、電子が1周する間に、簡単に八面体の構造が崩れてしまう。
もちろん、2つの水素原子の存在のため、上の酸素原子の初期条件をそのまま使うことはできない。(一度やってみるといい。)
要するに、正確な初期条件(各座標と、各速度ベクトル)を見つけることはとても難しい。
2つめに、各電子と水素原子核の距離はそれぞれ異なるため、酸素原子の6つの価電子は異なるエネルギーを持っている可能性がある。
つまり、我々は、結合エネルギー (=9.6066 eV) がどのように各電子に分配されるのか知る必要がある。
ビリアル定理 (Virial theorem) によれば、平衡状態では、平均の位置エネルギー (V) と、運動エネルギー
(T) は、-1/2 V = T の関係式を満たす。
水素原子や酸素原子の場合は、1つの原子核しかないので、この V を計算するのは簡単である。
しかし、水分子 (H2O) の場合は、この V は、原子核間のクーロン反発ポテンシャルエネルギーを含む必要があるため、少し事情が複雑だ。
問題は、この原子核間のエネルギーをどのように各電子に分配するかということである。
このプログラムでは、各電子の位置エネルギーを最初の座標から計算する。
O-H 結合を形成するには、2つの正電荷の原子核が、他の原子核に属する電子にひきつけられる必要がある。 (Fig. 8)
Fig. 8. O-H 結合と各位置エネルギーの変化
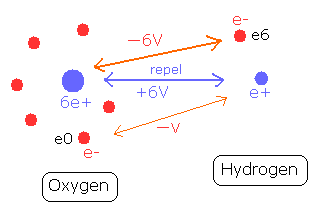
水素原子核 (e+) は、酸素原子の6つの電子に引きつけられる。
水素原子核と酸素の1つの電子 (e0) の間の位置エネルギーは -V である。
一方で、酸素原子核は、水素原子に属する1つの電子 (e6) によって引きつけられる。そのため、酸素原子核とこの電子 e6 の間の位置エネルギーは - 6V となり、この結合力は、上の場合の6倍も強い。
つまり、水素の電子 (e6) の位置エネルギーは O-H 結合で-6V も低くなる。しかし、そのかわり 電子 e6 は、2つの反発する原子核を結合させるのに 多くのしごとをしなければならない。よって、この影響でそれよりかは、少し位置エネルギーは高くなる。
この事実をもとに、このプログラムでは、電子ー電子間、電子ー原子核間の位置エネルギーを計算の後、反発する原子核間の位置エネルギーを各電子に分配する。
例えば、この反発するエネルギーが、+6V のとき、e6 と e0 の分配比は 6 : 1 (= -6V : -V) とする。
酸素は6つの e0 - e5 の電子を持つため、 +6V × 6/(1x6 +6) = +6V / 2 が e6 に分配され、+6V × 1/(1x6+6)= +6V / 12 が e0 に分配される。
その各位置エネルギーをもとに、運動エネルギーが分配される。
しかし、この方法は”平均的な”状態にのみあてはまる。
そこで、我々はこれらの値を少し調整する必要がある。
酸素のプログラムのように、今回もスクロールバーの中のド・ブロイ波の数を選び、”orbit” ボタンをクリックする。
最初に、なるべく小さな数を選択する。(例えば、1.9 や 2.0 でなく、0.3 や 0.5 を選ぶ)。
電子軌道を計算後、酸素原子のどれか1つの電子 (例えば e0) が他の5つの電子よりも核に近づいてしまうとすると、我々は、e0 の初期速度ベクトルの方向を 外側に少し変化させたり、もしくは、他の電子の運動エネルギーを少し (0.01 - 0.1 eV) 電子 e0 に移動させる。
初期の運動エネルギーを少し電子間で移動させるには、最後の行のスクロールバーの中から、電子の番号を選び (el0 - el7)、移動値 (eV) (例えば、0.1, 0.01, 0.2... など。) をその隣のテキストボックス内に入力して "Enter" キーを押す。
ただ、このプログラムを実行すると、自動的にすでに調整された値がテキストボックスにセットされる。
つまり、単にスクロールバーのド・ブロイ波の数 (wn) を選択し、"orbit" ボタンをクリックするだけでいい。
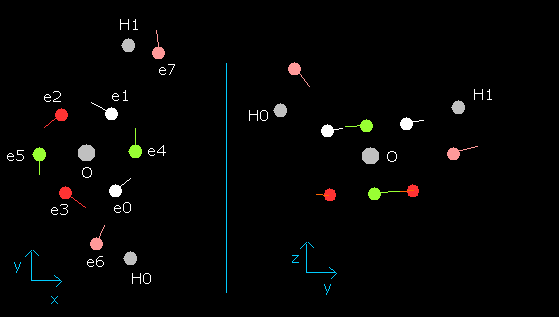
wn が 0.0 のとき (e0 の nuc は 4589 MM となる。)、電子状態は次のようになる。
Fig. 9. プログラム内の水分子 (H2O) の電子状態 (wn=0.0)
wn が 0.5 のとき、水分子の電子 e0 - e5 は、次のようにほとんど x-y 平面上にある。
Fig. 10. wn=0.5 のときの水分子 (H2O)
この状態 (wn=0.5) では、e0 の nuc は、4266 MM となる。
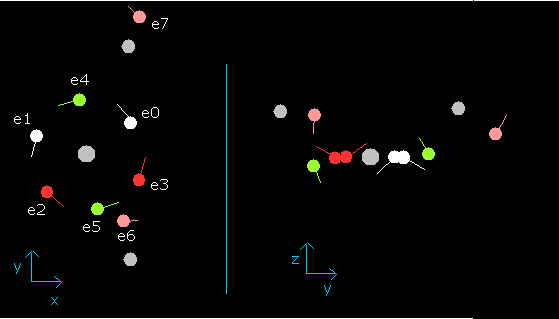
wn が 0.9 のとき、各電子の位置は、
Fig. 11. wn=0.9 のときの水分子 (H2O)
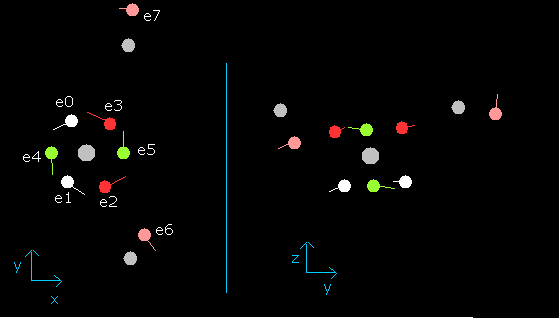
この状態 (wn=0.9) では、酸素の6つの価電子は、最初の位置からちょうど反対側にある。
また、nuc = 3949 MM は、最も短い距離である。
wn が 1.9 のとき、各電子の位置は、
Fig. 12. wn=1.9 のときの水分子 (H2O) ( = ほとんど wn=0.0 のときと同じ。)
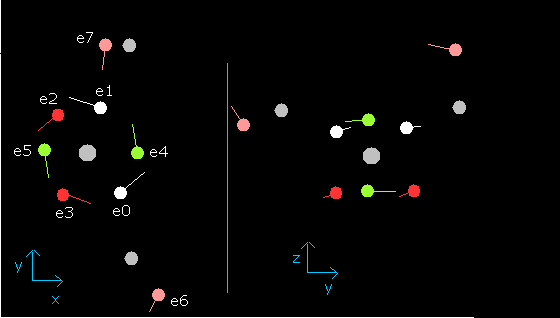
この結果は、水の酸素の軌道の長さは、ほぼ 2.0 ド・ブロイ波長である ことを示している。
(wn=2.0 のときは、電子は少し歳差運動する。もしくは、実質的中心電荷を上の酸素のように +6.3e にしたほうがよいだろう。)
電子 0 (e0) と原子核の最後の距離は、4588 MM であり、これは、4589 MM ( wn=0.0 ) とほぼ同じである。
このプログラムはコマンドプロンプトの画面に、水素の電子 6 (e6) のド・ブロイ波の結果も示す。
重要な点は、酸素の電子 (e0 - e5) は水素の電子 (e6, e7) よりも速度が速いということである。
そのため、電子 0 が 2.0 ド・ブロイ波長分の軌道を1周したとき、電子 6 は、0.6 ド・ブロイ波長分の軌道しか進んでいない。
おそい電子 6 は、この間にその軌道を1周できないということだ。
公転周期がそれらでは、違うことになる。
(注意すべきは、水素の電子の軌道長は、1.0 ド・ブロイ波長である。)
H2O のビリアル定理も参照のこと。
最初の状態では、各電子の位置エネルギー (V) と、運動エネルギー (T) は、テキストボックス内を見てもらうとわかるが、-1/2 V > T の関係にある。
つまり、この状態は、”楕円”軌道の長軸側にあたる状態と言える。
(実際に、wn=0.0 のときの nuc=4589 MM の値は、wn=0.9 のときの nuc=3949 MM よりも長い。)
また、テキストボックスの最後の行の (FX, FY, FZ) は、酸素原子核に作用する 力の各成分を示している。
ここでは、ボーア半径の水素原子を基準にして力を表している。
この水素原子内の電子と原子核間に働く力を 1000 として定義してある。
つまり、(FX,FY,FZ) =(-71, 98, -145) は、水の酸素原子核はほぼ平衡状態にあることを意味している。(酸素原子核に作用する力はほぼゼロに近い。)
メタン (CH4) 分子は、正四面体構造であり、炭素原子は 4つの水素原子に結合することができる。
しかし、水分子 (H2O) では、酸素原子は2つの水素原子としか結合することができない。
しかし、酸素のように6つの価電子を持つ硫黄 (S) は、2つよりも多くの原子と結合できる。
例えば、H2SO4 (硫酸)などなど・・・。
Fig. 13. 酸素様原子と炭素様原子
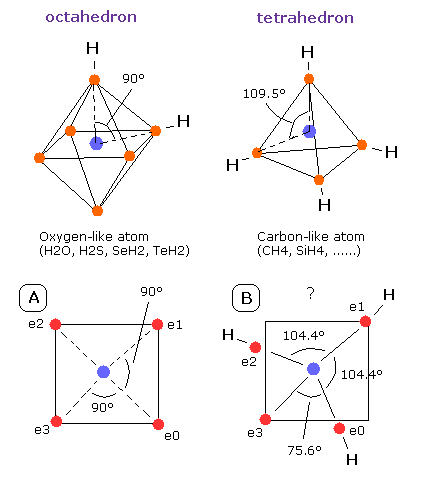
この硫黄 (S) と酸素原子 (O) の違いは何であろうか?
Fig. 13 に示すように、酸素原子は炭素原子に比べて、電子が混み合っている状態といえる。そのため、酸素の角度 (= 90°)は、炭素の角度(= 109.5°)よりも小さい。
これは、酸素原子には、他の原子と結合するスペースがあまりないことを示している。
しかし、硫黄 (S) では、6つの価電子は 3 ド・ブロイ波長のより大きな軌道に属しており、水素原子間の相互作用は酸素よりもかなり小さい。
実際に、硫化水素の H-S-H 角は、92.1° (ほぼ 90°)で、このことは、H2S においては、”八面体”の構造がほぼ保たれていることを意味する。
しかし、水の H-O-H 角は、104.45° であり、水では”八面体”の構造が少し壊れている。
(重要な点は、この 104.45° というのは、Fig.13 に示すように 90°(O) と 109.5°(C) の間の角度だということである。)
その状態で、もし3つめの水素原子が H2O に結合すると、この”八面体”構造はますます壊れることになる。(Fig. 13-B を参照のこと。)
この場合では、e0- 核 - e3 の角度は、"不自然に"75.6°ほどにも小さくなってしまう。
つまり、水分子においては、八面体の構造を何とか保つために、2つよりも多くの水素原子は酸素に結合できないと考えられる。

2010/10/8 updated This site is link free.