この定理は 古典力学と量子力学の両方において成り立つ。
複数の原子核や電子などの クーロン力 で相互作用しあっている多体系では、平均の全運動量 (T) と 平均の全位置エネルギー (V) は次の関係式を満たす。
(Eq.1)
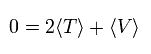
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは単なる幻想にすぎない。
ビリアル定理は 19世紀に Clausius によって考案された。
この定理は 古典力学と量子力学の両方において成り立つ。
複数の原子核や電子などの クーロン力 で相互作用しあっている多体系では、平均の全運動量 (T) と 平均の全位置エネルギー (V) は次の関係式を満たす。
(Eq.1)
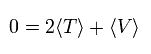
最初に、この定理を古典力学的手法によって証明する。
もしこれが証明できれば、この定理を 様々なボーア模型の分子において利用できることになる。
まず、次のような スカラー値 ( Cvir ) を定義する。
(Eq.2)
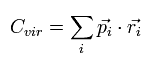
Eq.2 は 各粒子の 運動量 (pi) と 位置座標 (ri) の内積の合計を意味している。
( pi は i 番目の粒子の 運動量ベクトルを表している。)
Eq.2 の粒子の数 ( i = 1, 2, 3, ... ) は任意の数をとることができる。
(つまり、ビリアル定理は 複数の原子核と電子の混ざった分子などの系で通用する。)
Eq.2 の時間微分は次のようになる。
(Eq.3)
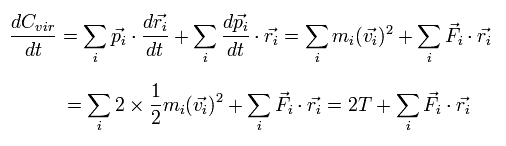
ここでは、次の関係式を使用している。
(Eq.4)
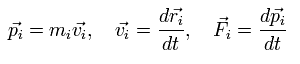
ここでは、 mi , vi , Fi は それぞれ 各粒子の 質量、速度ベクトル、力ベクトル (i 番目に粒子に作用する) を意味している。
例えば、i 番目の粒子が ”静止した”重い原子核だとすると、Eq.3 の i 番目の運動エネルギーはゼロになることになる。
( もちろん、この場合では i 番目の 力 (F) と r はゼロになる必要はない。)
Eq.3 の両辺を 0 から 時間 t の範囲で積分して その結果を t で割る。最後に t → ∞ の極限をとると、Eq.3 の左辺は次のようになる。
(Eq.5)
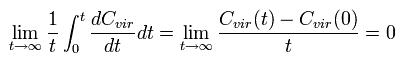
ここでは、分子は ”有限の”値で、分母は ”無限の”値 (t → ∞) である。
そのため Eq.5 はゼロになる。
( ある領域内の粒子の運動の系においては、C(t) の値が 有限になるのは しごくあたりまえの話である。)
一方で、Eq.3 の右辺の各項は 次のように 時間平均の値 になる。
(もちろん、それらの合計は 左辺のようにゼロになる。)
(Eq.6)
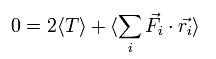
Fi は i 番目の粒子に作用する力の合計を意味している。
そこで、この Fi を Fij の力ベクトルに分解することができる。
この Fij は i 番目の粒子が j 番目の粒子から受ける力のベクトルを意味している。
すると、力 (F) と 位置 (r) のベクトルの内積は次のように表せる。
(Eq.7)
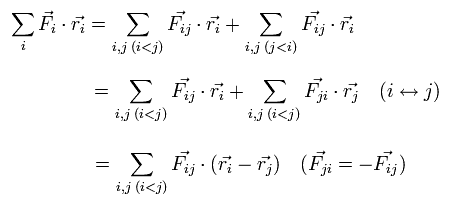
もし、Fij が i 番目と j 番目の粒子間の クーロン力 を意味しているとしたら、Fij は次のようにあらわせる。
(Eq.8)
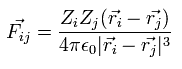
ここで Zi は i 番目の粒子の 電荷 を意味している。
Eq.8 を Eq.7 に代入する。
(Eq.9)
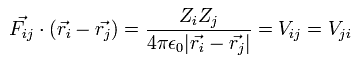
ここで Vij は、i 番目 と j 番目の間の クーロン位置エネルギー を意味している。
Eq.9, Eq.7, Eq.6 を使うと、次に示すように 最終的な ビリアル定理 を得ることができる。
(Eq.10)
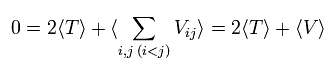
(Eq.11) 水素様原子の基底状態。
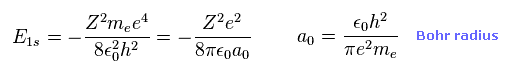
ここで シュレディンガーの水素原子の波動関数が ビリアル定理 ( E = 1/2 V ) を満たすことを示す。
Eq.11 は 原子番号 Z の 水素様原子の基底状態 ( n = 1 ) のエネルギー である。
もちろん、このエネルギー準位は ボーア模型に完全に等しい。
また a0 は ボーア半径である。
(Eq.12) シュレディンガーの 1s の波動関数。
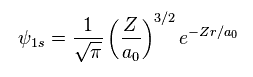
シュレディンガーの 1s の波動関数は Eq.12 のようになることが知られている。
Eq.12 を用いると、平均的な位置エネルギー V は
(Eq.13)
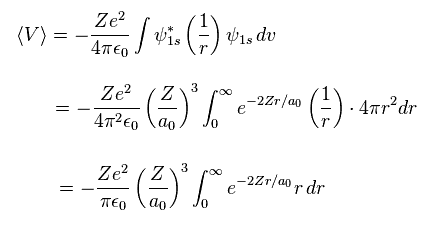
ここでは
(Eq.14)
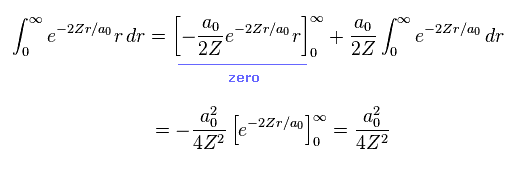
Eq.13 と Eq.14 から、位置エネルギー V は、
(Eq.15)
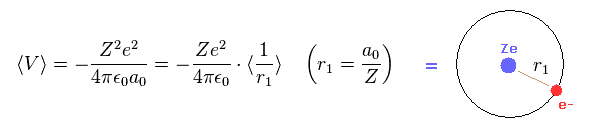
Eq.15 は 1s の波動関数 (= Eq.12 ) の平均的な確率密度が a0/Z になることを意味している。
( Z は原子番号である。 水素原子では Z = 1。 )
もちろん、この結果は ボーア模型の水素と同じである。
Eq.11 と Eq.15 から、シュレディンガーの水素も ビリアル定理を満たすことを示せる。
(Eq.16)
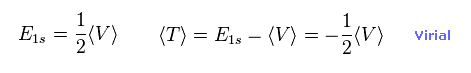
Eq.16 の結果は 量子力学的な変分法が ボーア模型と似た結果を与える主要な要因である。このページも参照のこと。
次に 量子力学において ビリアル定理を証明する。
1927 年、エーレンフェストは 古典的な粒子の運動を 量子力学的な波動に結びつけた理論を示した。
すなわち、基本的な原理は それらで同じであることを意味している。
ここでは 次に示す ハミルトニアン演算子 (H) と 運動量演算子 (p) を使用する。
(Eq.17)
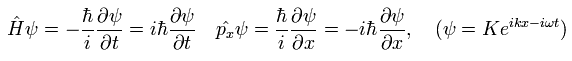
任意の演算子 A の 期待値全体の時間微分は Eq.17 を使って次のように表せる。
(Eq.18)
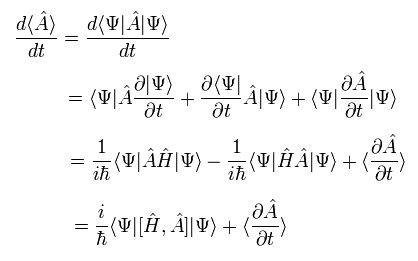
ここでは ハミルトニアンの複素共役も使用している。
演算子 A は 直接的な時間変数 を含んでいないため、Eq.18 の最後の項はゼロになる。
ここでは 演算子 A として、運動量 (p) と 位置 (r) の内積を使用する。
すると、Eq.18 の結果は次のようになる。
(Eq.19)
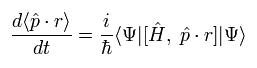
Eq.19 の交換子は次のように表せる。
(Eq.20)
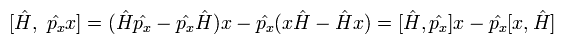
Eq.20 の ハミルトニアンと運動量の交換子は次のようになる。
(Eq.21)
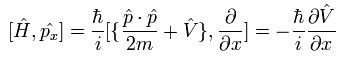
ここで V は 位置エネルギーを意味している。
また、Eq.20 の ハミルトニアンと位置演算子の交換子は次のようになる。
(Eq.22)
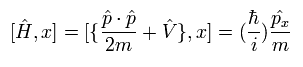
Eq.22 に到達するには 次の交換関係を使用する必要がある。
(Eq.23)
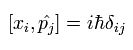
Eq.23 を使用して 次の交換子を計算する。
(Eq.24)
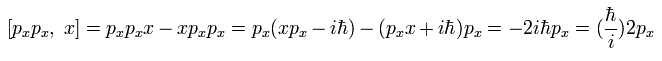
Eq.23、Eq.24 を使用して、Eq.22 の結果を得ることができる。
Eq.21, Eq.22 を Eq.20 に代入すると、Eq.19 の結果は次のようになる。
(Eq.25)
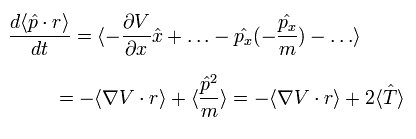
もし V として、クーロン位置エネルギー を使用すると、次の値を得ることができる。
(Eq.26)
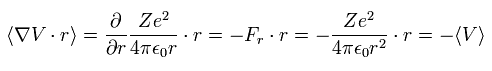
Eq.5 のように、Eq.25 の左辺は 定常状態では ゼロになる。
結果として、量子力学においても ビリアル定理にたどりつける。
(Eq.27)
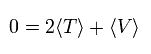
シュレディンガー方程式は クーロン位置エネルギー のみを使用して、クーロン力を使用しないという人たちが中にはいるかもしれない。
彼らは、これが量子力学と古典力学の違いだと主張している。
しかし、Eq.26 に示すように、量子力学のビリアル定理を得るには、計算過程で クーロン力を使用しなければならない。

2011/2/15 updated This site is link free.