トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。単なる数学上の産物。
古典的軌道による生体金属錯体。
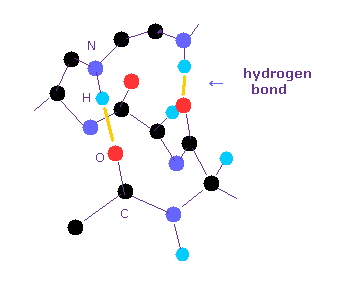
(Fig.1) タンパク質内の水素結合。

水素結合は非常に弱いため 短いタンパク質では 水素結合を形成しずらい。
ある程度長いタンパク質において、疎水性のタンパク質に囲まれた部分で 親水性の部分同士が 水素結合を起こす傾向にある。
また 他の親水性の残基は 周囲の水と水素結合を形成する。
一般的に 水素結合の形は " O -- H-O "、 " N -- H-N "、 " O -- H-N" などである。
もちろん、これらの水素結合は すべて その中間部分に 水素原子を含んでいる。
どうして 水素原子が これらの結合を引き起こしやすいのだろうか?
(Fig.2) N --- H - N 水素結合。
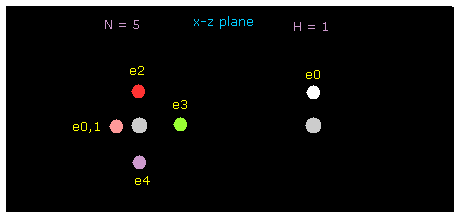
このセクションでは 水素結合を調べるために このサンプルプログラム を使用する。
このプログラムを "twobin.java" としてセーブしてコンパイルしてほしい。 "--Xlint: unchecked ---" などの注意は無視して実行できる。
操作方法は このページと 同じである。
(Fig.2') 力 = 1000.
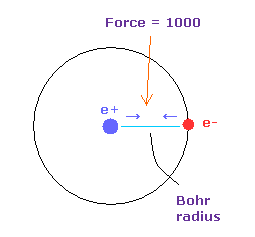
力の単位は Fig.2' に示したものである。
水素原子の基底状態で 電子と原子核間に作用している力を
"1000" とした。
つまり 電子と +e 原子核間の距離が ボーア半径のとき、 その力は 1000 になる。
例えば 力 1468 は H 原子の基底状態の 1.468 倍の力である。
新しい単位 1 MM = 1.0 × 10-14 meter を使用している。
(Fig.3) N --- H - N (= 窒素 ) の水素結合。
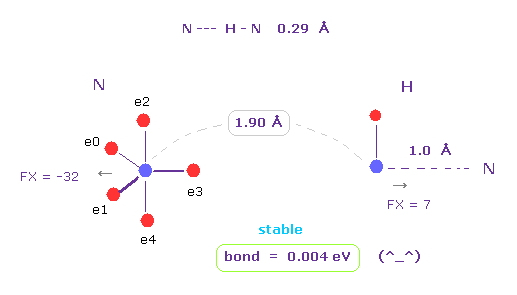
上記のプログラムを実行して、A と B 原子として "N" (= 窒素 ) と "H" を選択する。
N -- H-N 長は 約 0.29 - 0.30 Å であるため、 N と H 間の核間距離として 1.90 Å (= 19000 MM ) を選ぶ。 (= そして "internuc" ボタンをクリックする。 ).
なぜなら そこから 1.0 Å N-H の共有結合分を 差し引くからである。
Fig.3 に示したように、結合エネルギーは わずかに 正の値 (= 0.004 eV ) になる。 これは この結合が安定であることを示している。
( ここでは 水素の電子を収縮させたり、移動させたりは考慮していないため、この結合エネルギーは 実際の値より少し小さくなる。)
各原子核は 互いに少し反発し合っている、しかし それらは ほぼゼロである。
( FX = -32 と FX = 7。 )
(Fig.4) "H" 原子を "C" 原子に変更する → "不安定"に。
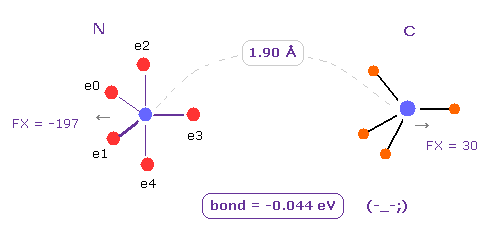
次に H 原子を 炭素原子 (= C) に変更する。
"C" を選んで "Atom B" ボタンをクリックする。
このケースでは、結合エネルギーは 負 (= -0.044 eV ) になるため この結合は 不安定ということになる。
このプログラムでは "A-tV" と "B-tV" は A と B 原子内でのみの 全ポテンシャルエネルギーである。
"ABen" ( "ABne" ) は A-電子 (原子核) と B-原子核 (電子) 間の ポテンシャルエネルギーである。
"ABee" ( "ABnn" ) は A-電子 (原子核) と B-電子 (原子核) 間のポテンシャルエネルギーである。
N-C 結合では、A と B の 電子間の反発力 (= ABee ) が N-H 結合よりも 大きくなるため 不安定になる。
(Fig.5) "H" 原子を "O" 原子に変えると ? → "不安定"。
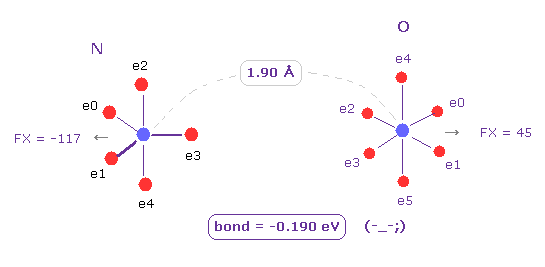
次に C 原子を 酸素原子 (= O ) に変える。
"O" を選んで、 "Atom B" ボタンをクリックする。
この場合も 結合エネルギーは 負 (= -0.190 eV ) になり、これはつまり この結合も 不安定であることを意味している。
ご覧のとおり、 1.90 Å の長い結合長では、 電子間の反発力が N-C と N-O 結合では 優位になる。
このことが 正電荷の原子核をさらけ出している水素原子が 水素結合として選ばれた主要な要因である。
| N - A 長 | 2.20 Å | 2.10 Å | 2.00 Å | 1.90 Å | 1.80 Å | 1.70 Å | 1.60 Å |
|---|---|---|---|---|---|---|---|
| N - H | -0.006 | -0.004 | -0.001 | +0.004 | +0.013 | +0.029 | +0.055 |
| N - C | -0.133 | -0.117 | -0.09 | -0.044 | +0.031 | +0.154 | +0.355 |
| N - O | -0.197 | -0.199 | -0.197 | -0.190 | -0.173 | -0.138 | -0.069 |
Table 1 に示したように、炭素や酸素などの他の原子は 価電子による反発力が より強くなる。 そのため N と 安定な 水素様結合を形成できない。
一方で、たった1つの電子である水素は 長い結合長 (= 1.90 Å ) においても、 安定な水素結合を形成することができる。
( 炭素は しばしば 4つの原子で 囲まれているため、 N などが この炭素に近づくことができない。 )
基本的に、結合長が 短くなり、実際の共有結合長に 近づくにつれて 結合エネルギーは 大きくなる。
( 共有結合長は N-C で 1.47 Å、 N-O で 1.40 Å である )。
そのため 安定な共有結合を形成するためには、各原子は ある閾値の長さよりも 互いに より近づく必要がある。
(Fig.6) H -- O-H 水素結合。
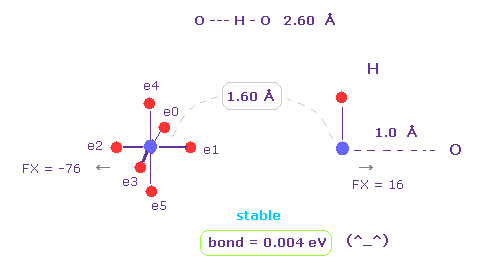
H -- O-H 水素結合長は 約 2.60 - 2.70 Å である。
A と B 原子 として "O" と "H" を選び、 核間距離を "1.60 Å" (= 16000 MM ) にする。
x-y 平面上で "O" 原子を 45°回転する ( "45" を入力して "x-y ang" ボタンをクリックする。 )
このケースにおいても、結合エネルギーは 正 (= 0.004 eV ) になり、O-H 結合は 安定になる。
また 原子間の反発力は ほぼ ゼロ ( FX = -76, FX = 16 ) になる。
( これらは ほぼゼロだが、わずかに "反発" しているため、 O-H や N-H 結合長は これ以上 短くなれない。 )
(Fig.7) 長い結合長では、O - C 結合は "不安定" である。
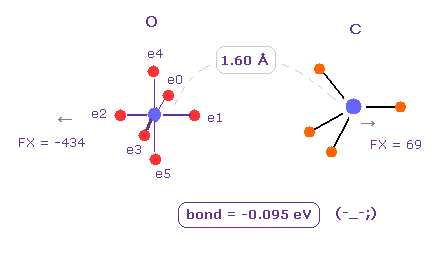
次に H 原子を C 原子に変更する ( "C" 選んで "Atom B" ボタンをクリックする。 )
このケースでは 結合エネルギーは 負 (= -0.095 eV ) になる。
そのため 上で述べたように、価電子間の 反発力は そのような長い O-C 結合長においては 強くなる。
( もちろん 酸素は 4つの他の原子に囲まれている炭素に近づけないが。 )
(Fig.8) O - O 結合も "不安定" である。
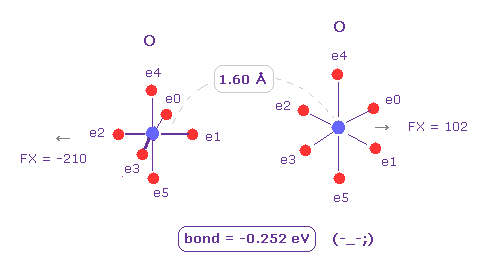
次に "O" (= 酸素 ) を Atom B として選ぶ ( "O" を選んで "Atom B" ボタンをクリックする )。
この場合においても、結合エネルギーは 負 (= -0.252 eV ) になり、これは 不安定である。
つまり この長い結合長では、O-C と O-O 結合においては、電子間の反発力が 優位になる。
| N - A 長 | 1.90 Å | 1.80 Å | 1.70 Å | 1.60 Å | 1.50 Å | 1.40 Å | 1.30 Å |
|---|---|---|---|---|---|---|---|
| O - H | -0.011 | -0.009 | -0.004 | +0.004 | +0.022 | +0.054 | +0.113 |
| O - C | -0.205 | -0.190 | -0.158 | -0.095 | +0.020 | +0.232 | +0.612 |
| O - O | -0.261 | -0.266 | -0.265 | -0.252 | -0.215 | -0.122 | +0.092 |
Table 2 に示したように、長い結合長 (= 1.60 Å) においても、 O-H 結合は その露出した原子核のために 安定である。
C や O などの他の原子では 価電子間の反発力が優勢になる。
このケースにおいても、結合長が 短くなると、その結合が 共有結合様になり 安定化する。
(Fig.9) どうやって 原子は立体障害と共有結合を区別するのか?
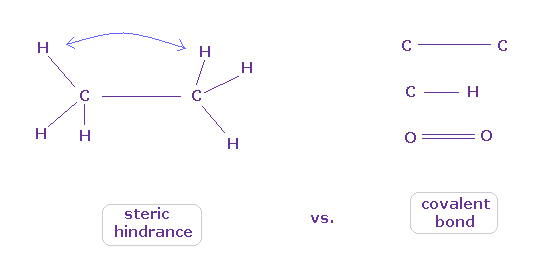
よく教科書で "エタンの6つの水素原子は 互いに避け合う配置をとる" とか "タンパク質の構造は その立体障害のために 非常に制限される " だとかの説明を見られるかもしれない。
これはつまり 各原子は 必ず 他の原子を避ける傾向があるということだろうか?
一方で 希ガス原子を除いて 様々な原子は 安定な共有結合を形成することができる。
各原子が 互いに"避け合う"のに、どうして それらは 安定で タイトな共有結合を形成することが可能なのだろうか?
これらの違いは 上で述べたように それらの結合長に依存していると言っていい。
(Fig.10) C-C = 1.5400 Å は 釣り合いのとれた長さである。
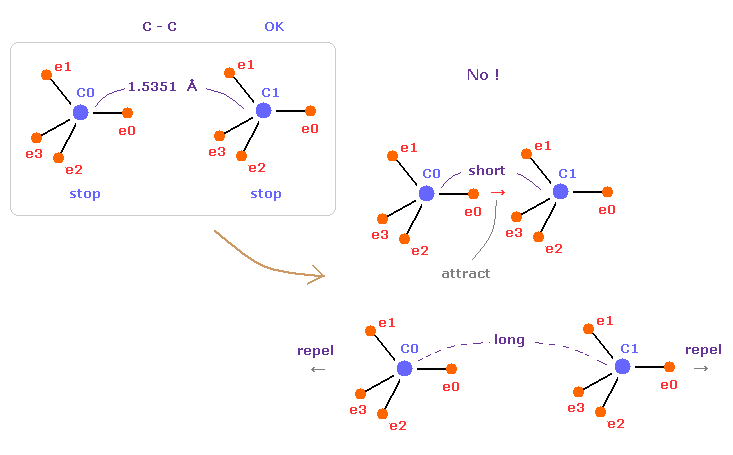
このページでは エタンの C-C 結合長 1.5351 Å が 両方の C 原子核の安定性にとって 必要不可欠なものであることを示した。
もし C-C 結合長が 1.5351 Å よりも短くなると、e0 と C1 間の引力が 強くなりすぎ、不安定になる (= 結合エネルギーは大きくなる )。
そして もし C-C 結合長が これよりも長くなると、2つの C 原子核間の反発力が優勢になり 不安定になる (= 結合エネルギーが 負の値になる。)。
これが C-C 結合長を決定する 本当のメカニズムである。
(Fig.11) いつ C-C 結合長は 安定になるのか?
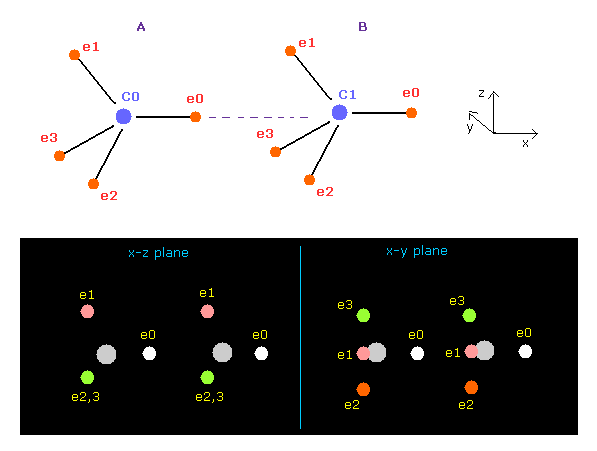
上記のプログラムを実行して 各炭素原子に作用する力を計算する。
A と B atom 両方に "C" と "C" を選ぶ。
| 核間距離 (MM) | A 核への力 | B 核への力 | その差 |
|---|---|---|---|
| C-C 15351 | FX = -340 | FX = -341 | = -1 |
Table 3 に示したように、 C-C の核間距離が 実験値 (= 1.5351 Å ) のとき、A と B 原子核に作用する力の x 成分 (FX) は ほぼ同じ -340 と -341 になり、これは 安定した核間距離を意味している。
| C-C (MM) | A 核の FX | B 核の FX | その力の差 |
|---|---|---|---|
| 12000 | -856 | -1703 | -847 |
| 13000 | -633 | -1013 | -380 |
| 14000 | -479 | -627 | -148 |
| 15000 | -370 | -399 | -29 |
| 15351 | -340 | -341 | -1 ← |
| 16000 | -292 | -258 | +34 |
| 17000 | -234 | -168 | +66 |
| 18000 | -191 | -109 | +82 |
| 19000 | -158 | -69 | +89 |
C-C 核間距離 (MM) の値を 指定のテキストボックス内にいれて "internuc" ボタンをクリックすると、結合長を自由に変更できる。
Table 4 は A と B 原子核に作用する力の成分 FX の差を示したものである。
核間距離が短くなると、この違いは マイナスになる。
( これはつまり C 原子核と価電子が引かれすぎて 共有結合が 不安定になることを意味している。)
(Fig.12) C-C 結合長が実験値 = 1.5351 Å のとき。
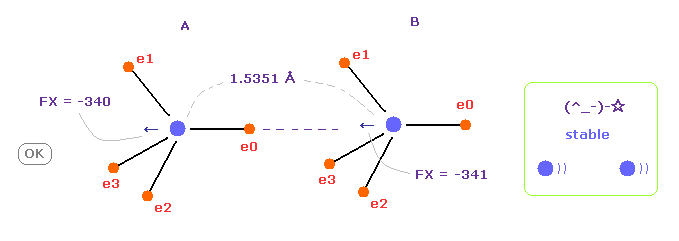
C-C 結合長が実験値のとき、 A と B 原子核に作用する力は ほぼ 同じになる。
( FX = -340 と -341 ).
これはつまり C-C 結合長が 平衡状態で安定であることを示している。
また この結果は クーロン力と ドブロイの関係式が 実際の C-C 結合でも有効であることを示している。
(Fig.13) C-C 結合長が短くなると = 1.4000 Å
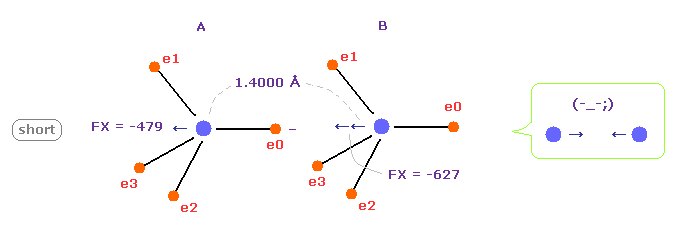
C-C 結合長が実験値より 短くなると (= 1.4000 Å )、 B の原子核は A 原子の 電子 e0 に 強く引かれすぎることになる。
これはつまり このケースでは C-C 結合長は さらに短くなろうとして不安定になってしまう。
(Fig.14) C-C 結合長が長くなると = 1.7000 Å → それらは反発し合う。
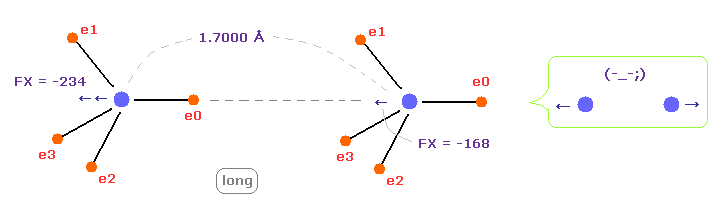
C-C 結合長が実験値より 長い (= 1.7000 Å ) とき、 2つの原子核間の 反発力が 強くなる。
このケースが 上の水素結合のセクションに当てはまる。
一般的に 上で述べたように 結合長が長くなるにつれて、結合エネルギーが 負 になる傾向がある。
これはつまり C-C 結合長が このケースでは不安定になってしまうことを意味している。
結果的に C-C 結合長が実験値のとき、その距離は安定になる。
(Fig.15) 上下の状態が交互に繰り返す。
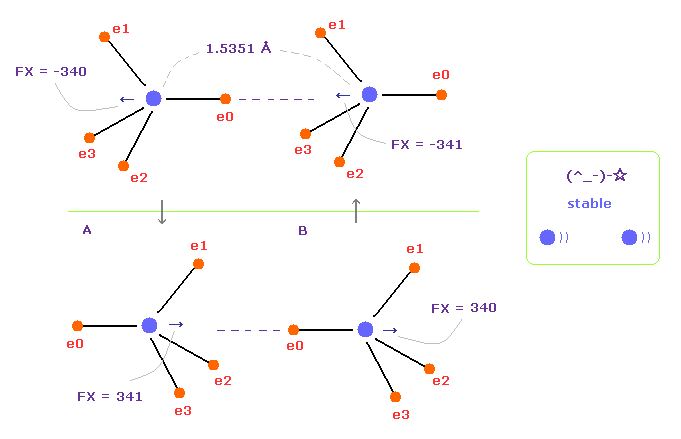
Fig.12 の全体の力は マイナス x 方向である。
しかし 価電子は 各原子核の周囲を運動しているため、Fig.15 の上下の状態を繰り返すことになる。
Fig.15 の上下の状態を足し合わせると、トータルの原子核に対する力は ほぼゼロになる。
(Fig.16) "長い" か "短い" か の結合長が その性質を決定する。
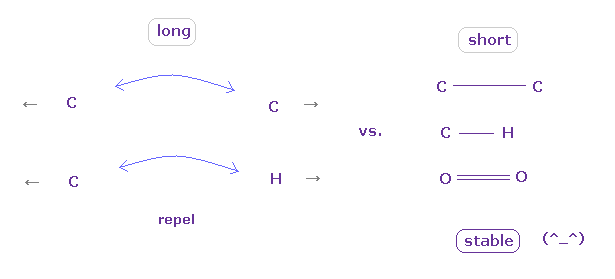
結論からして、安定な結合を形成するには、2つの原子が ある閾値の長さよりも 互いに 接近する必要があると言える。
その閾値の長さよりも 長いと、 電子間や核間の反発力 が 優勢になり、いわゆる 立体障害を引き起こす。
通常のタンパク質では、2つの原子間の ほぼすべての距離は 共有結合長よりも 長いため、それらは 立体障害を引き起こす。
(Fig.17) 無限の 裸の電荷と質量 + "間違った" 数学 = QED.

量子電磁力学 (QED) は 量子力学と 特殊相対論の正確なテストに一致し、物理学史上 最も成功した理論の1つである というコメントをしばしば見られることと思う。
しかし このページに示したように、 QED は 非常に小さな値を得るために 無限大を無視している。
また 特殊相対論に反する仮想光子に完全に依存しているのである。
さらに、QED は 完全に "間違った" 数学に依存している。
このページでは QED が 間違った数学に依存していることを確認してみる。
もし QED の g因子が間違っているとすると、その g因子の計算結果は ラムシフトの値の一部としても使用されているため、QED の ラムシフトも間違いということになる。
(Eq.1) QED における "人為的"なトリック。

Eq.1 は QED の g因子 (= 異常磁気モーメント ) の計算における 根本的な計算ミスを示している。
Eq.1 上では 奇関数 "k" の積分は ゼロになる。
( ローレンツ変換不変性の要求により この積分範囲は -∞ から +∞ までである。)
変数変換 ( k = l - β ) の後、 奇関数のために " l " の部分はゼロになる。
結果的に "-β" の部分のみが残り、ここには g因子の情報が 含まれている。
この数学的手法は QED の g因子を得るのに 必要不可欠なものである。
もちろん、 Eq.1 の数学は 間違いである。なぜなら "変数変換" というのは 単なる手段で それによって計算結果自体が変わることは あり得ないからである。
(Eq.2) 正しい数学。
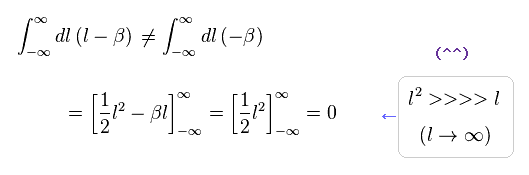
もし 正しい数学を用いれば、もちろん "-β" の項もゼロになることはいうまでもない。
なぜなら、それらを積分すると、 " l2 " の項が " βl " の項の部分よりも はるかに早く発散するからである。
結果的に 積分計算後、" l2 " の項のみ残り、この結果はゼロになる。
( 正しい数学によれば、 "β" の部分は "l" の項に吸収されてなくなってしまう。 )
つまり Eq.2 の QED の数学的手法は 数学の基本を破っているのである。
(Eq.3) "間違った" 数学を 実際の QED の計算に応用する。
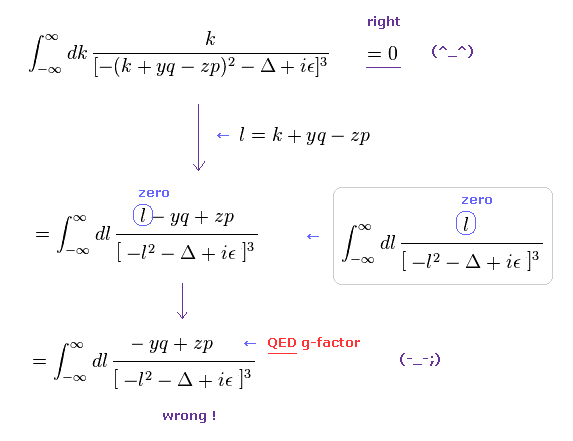
このページに示したように、Eq.3 のように、 Eq.1 の間違った数学を QED では 活用している。
"正しい"数学によれば、Eq.3 の最初の式は ゼロになる。
( "k" を除いた 他の値 (= y, q, z, p, Δ ) は 有限の値である。 )
しかし もし この"正しい"数学を用いると、QED の g因子を得ることができない。
QED の g因子では、変数変換 ( k + yq - zp → l ) をして、一般人が 容易に気づかないように 巧妙に 間違った数学を用いる必要がある。
Eq.3 の2行目では、 分母は l2 の偶関数で、 分子は "l" の奇関数であるため、分子の "l" の部分のみを ゼロにして 残りの "- yq + zp" の部分を g因子の一部として使用している。
( もちろん、この数学は 間違いである。 )
(Eq.4) 部分積分
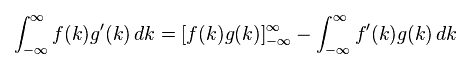
ここで Eq.4 の部分積分を用いて、 Eq.3 が ゼロになることを証明する。
( もちろん、有理関数の積分公式を 直接用いても Eq.3 がゼロになることを証明することができる。 )
(Eq.5)
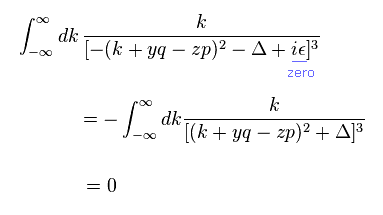
ここでは 無限小の ε の部分をゼロとする。
Eq.4 の部分積分を Eq.5 に使用する。
(Eq.6)
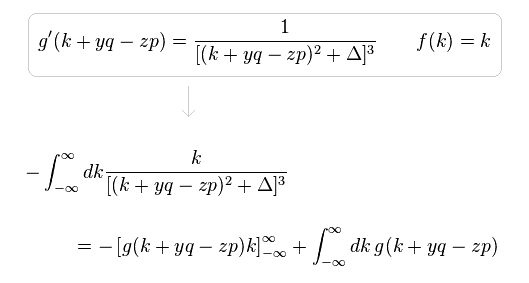
Eq.6 では、"k" が ±∞ に近づくにつれて、"k+yq-zp" と "k" の差は 次のように ゼロになる。
(Eq.7)
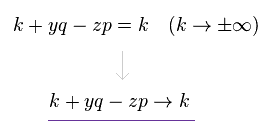
そのため g(k+yq-zp) のところで Eq.7 の変数変換を 同じ計算結果を保ったまま 行うことが可能である。
結果的に Eq.6 は 次に等しくなる。
(Eq.8)
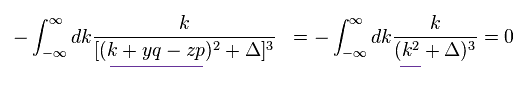
Eq.8 の分母は "k" の 偶関数である。
Eq.8 の分子は "k" の 奇関数である。
そのため Eq.8 は ゼロになり、 これはつまり Eq.3 (= Eq.5 ) も ゼロになることを意味している。
よって Eq.3 の QED の計算は 間違いということになる。なぜなら それは g因子の値を "人為的" に残すために ゼロにしていないからである。
Eq.5 は Eq.9 のように表すことができる。
(Eq.9)
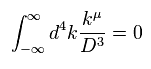
ここでは
(Eq.10)
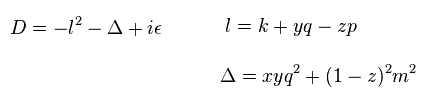
Eq.10 では、 x, y, z は x + y + z = 1 を満たし、 各値は 0 から 1 の範囲である。
( このページ (Eq.74) も参照のこと。 )
(Eq.11) g因子の計算式の 分子 の部分。
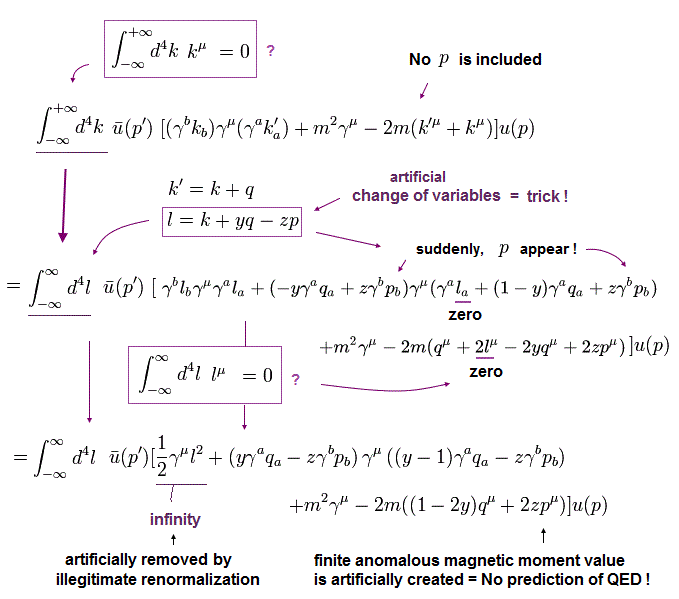
このページ (Eq.3)に示したように、正確なg因子の値を得るには Eq.11 の 2行目を 分子の部分として導出する必要がある。
しかしもちろん、この数学は 間違いである。
もし Eq.5 の正しい数学を適用すると、この結果は 完全に 異なったものになる。
ここでは これを証明する。
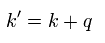
Eq.11 では、 "q" は 光子で "p" は電子、 "k" は 電子の伝播関数である。
このページ ( Fig.18、 Eq.36 )に示したように、 Eq.12 が満たされている。
(Eq.13)
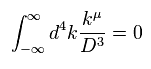
Eq.10、 Eq.12、Eq.13 (= Eq.6 ) を用いて、 Eq.11 を Eq.14 のように変更できる。
(Eq.14) "正しい" 数学。

Eq.14 の最初の行では Eq.5 と Eq.6 で説明した通り 奇関数 "k" の積分はゼロになる。
さらに Eq.13 と Eq.15 を用いると、無限大 (= l2 の部分 ) のところを除いて ほぼすべての値は ゼロになる。
(Eq.15)
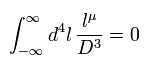
もちろん Eq.5 で 分子の ( k + yq - zp ) の部分を ただの "k" に変えても この結果は ゼロになる。
なぜなら 無限大は 有限の値を 吸収するからである。
つまり Eq.13 を満足すると、Eq.15 も当然成り立つ ( Eq.8 も参照のこと )。
(Eq.16) "正しい" 数学 = g因子が どこかに "なくなる"。

結果的に、Eq.3 の上の式の "正しい"数学を使用すると、正しい g因子の値を得ることができないということになる。
なぜなら Eq.16 の最後の行で示したように それは "p" (= 頂点に入る電子 ) を全く含んでいないからである。
結果、精密試験に最も成功したと言われる QED の g因子は 単なる計算ミスということになる。
(Eq.17)
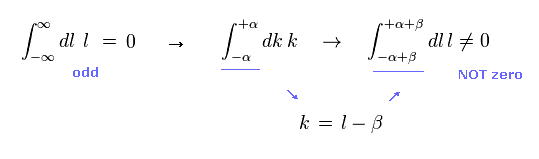
QED の g因子は Eq.15 のみを使用して、 Eq.13 は 間違いであると見なしている。
しかし この考え方は 自己矛盾している。
なぜなら Eq.15 を使用するには 積分の変数変換をした際に 有限の値を 無視しなければならないからである。
彼らは Eq.15 を得るために 有限の値を無視しておきながら、Eq.13 のケースでは 無視していないのである。
これは 明らかに 自己矛盾であり "人為的な" トリックの1つである。
このトリックに加えて、g因子を得るには 仮想光子を "ゼロ" にしなければならない。
しかし このとき、g因子 ( と ラムシフト ) の値は 任意の値をいくらでも取ることが可能になり 1つの値に決まらなくなってしまう。
( このページ ( Fig.11 - Eq.18 ) も参照のこと。 )
(Fig.18) なぜ 彼らは 重要な新事実を "反射的に" 捨て去るのか?
最近の興味深い実験によれば、様々な現象が QED に 一致しなかった。
(Pohl, R. et. al. Nature 466, 213-216 (2010), J. K. Webb, et.al. Phys. Rev. Lett. 107, 191101 (2011), C. T. Chantler, et.al. Phys. Rev. Lett. 109, 153001 (2012) ).
想像するに これら 従来の量子論や相対論に一致しない実験結果を発表するのは 非常に困難なことだったと思われる。
つまり 彼らは 非常に勇気があり、かつ 尊敬に値するといえる。
最初に このページに示したように、特殊相対論は 致命的なパラドックスを含んでいる。
そのため、従来の QED に一致しない実験結果が もっと出てきても不思議はないのである。
様々なジャーナルは "固定観念" にとらわれず、もっと実験結果を 公平に判断する必要がある。
また 私たちは 特殊相対論が 絶対的に正しいという 固定観念に惑わされることなく、超光速のニュートリノのような 真の実験結果を わずかな 反論結果のみで 諦めさせることはやめるべきと思われる。

2013/6/7 updated This site is link free.