トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは幻想である。
ヘリウム原子には 安定した化合物が存在しない。
量子力学は スピンアップとダウンの2つの電子を含んだ 1S の電子殻が この安定かつ強固な性質を生じさせると言っている。
しかし、これ以上具体的な理由については何も述べていない。
例えば、水素分子 (H2) においても、スピンアップとスピンダウンの電子が 1つの安定した結合構造を形成する。
しかし H2 分子は 酸素と容易に爆発的に反応する。
スピンの磁気モーメントは 小さいため、 ヘリウム原子と他原子との結合を防ぐ効果はない。
ということは ヘリウム原子はどうして 他原子(もしくはヘリウム自身)と化合物を形成できないのであろうか?
ヘリウムの 沸点と融点は原子の中で最も低い。
もちろん、自然界のいわゆる”4つの力”で、この理由を説明することはできない。
このページでは、我々の新しいボーアのヘリウム模型を用いて この理由について適切に説明することにする。
水素原子の基底状態は ちょうど1ド・ブロイ波長の軌道を持つ。
(このページに示したように、このことは ボーア模型とシュレディンガーの水素の両方にあてはまる。)
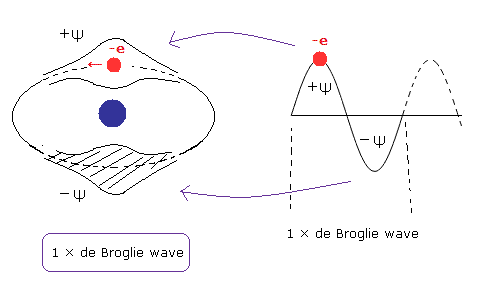
(Fig.1) 1ド・ブロイ波長の1軌道には 1つの電子が含まれる。

もし、この基底状態の軌道が 1つ以上の電子を含むとしたら、1つの電子の軌道長は元のものより短くする余地があることになり、基底状態がもっと低くなり得ることを意味する。
また、2重スリットや Davisson-Germer の干渉実験によれば、電子は必ず 1ド・ブロイ波長の範囲の中の ある限られた区間(位相)のほうに 押し込まれている。
ここでは この限られた区間(位相)を Fig.1 に示すように +Ψ と呼ぶことにする。
(もちろん +Ψ は -Ψ や +Ψ そのものと 干渉することができる。)
(Fig.2) 古いボーアのヘリウム模型。
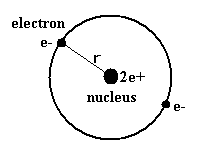
トップページに示したように、Fig.2 の古いヘリウム模型は 不正確なエネルギー値を与える。(= -83.33 eV.)
(中性ヘリウムの実験値は -79.005147 eV である。)
Fig.2 軌道では、2つの電子が 1ド・ブロイ波長の 1軌道に押し込められている。
そのため Fig.1 を考慮すると、+Ψ と -Ψ の位相が互いに干渉して打ち消し合ってしまう。
結果として、Fig.2 の軌道には 電子が入るスペースがない。( Fig.3 も参照のこと。)
(Fig.3) 古いボーア模型のヘリウムには 電子の入るスペースがない。
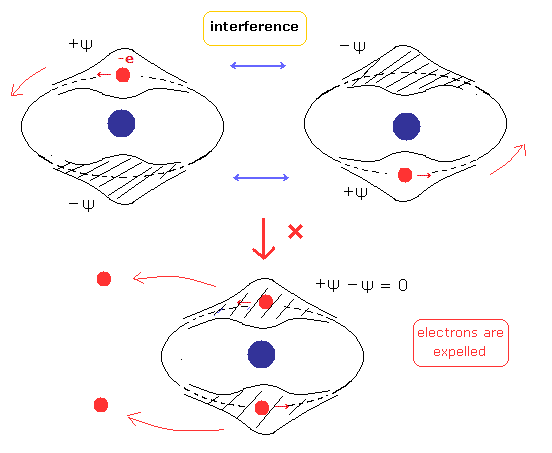
しかし、もしヘリウムの2つの軌道が Fig.4 にように 互いに 垂直だとしたら、2つの ド・ブロイ波は 互いに干渉しない。
結果として、互いに 独立した2つのド・ブロイ波は 安定かつ周期的に振動することができる。
(Fig.4) 安定かつ独立した 2つのド・ブロイ波。 (= 互いに垂直)
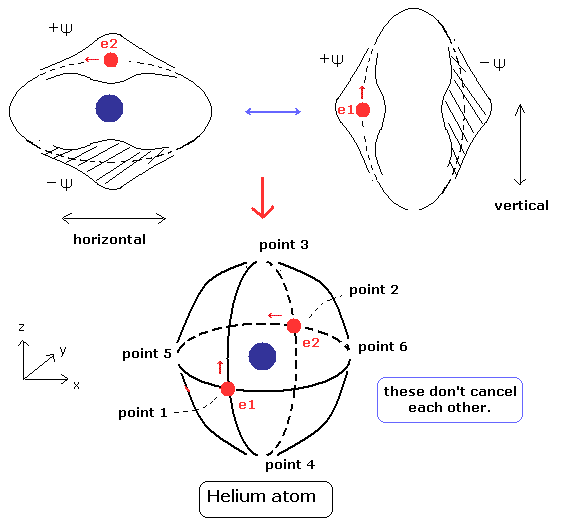
トップページに示したように、Fig.4 のヘリウム模型は 最も正確な結果を与える。(= -79.0035 eV, 相対論的補正は -0.001647 eV)。
(もちろん、この結果は シュレディンガー方程式を基にした最新の変分法よりも正確な結果である。)
また、Fig.4 模型は ヘリウム原子の 閉殻性 と パウリの排他原理を正確に説明することが可能である。この詳細は後で述べるとする。
Fig.4 のヘリウムには、2つの 交点が存在する。( point 1 と point 2 )
(Fig.5) Fig.4 の 交点 point 1 の状態。
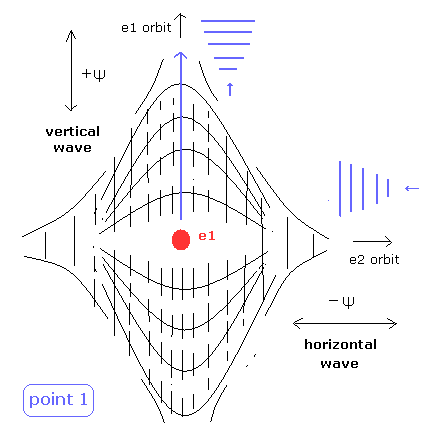
Fig.5 では、垂直な (= vertical ) ド・ブロイ波は 電子1 (e1) で、水平な (= horizontal) 波は 電子2 (e2) である。
+Ψ と -Ψ の位相は互いに垂直である。
そのため、それらは互いに打ち消し会わず、Fig.5 に示すように 電子1のスペースを与えることができる。
もし、Fig.5 において 電子1の速度の水平成分が完全にゼロでないとき、このことは 水平方向に 電子1の +Ψ の空間が存在することを意味する。
しかし、point 1 の水平方向の位相は 逆 (-Ψ) であり、そのため そのスペースが存在しない。
(+Ψ × 2 が必要である。 +Ψ × 2 - Ψ = +Ψ。しかしもちろん これは存在しない。)
結果として、2つのド・ブロイ波は 互いに ちょうど垂直になる必要がある。
(Fig.6) Fig.4 における 交点 point 2 の状態。
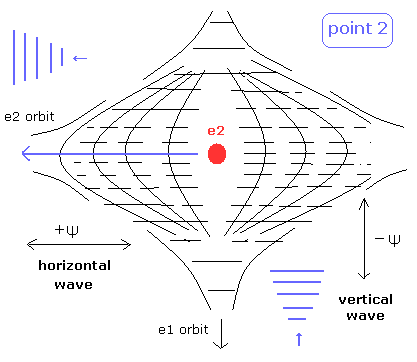
Fig.4 の point 2 においても、2つの ド・ブロイ波は互いに垂直である。
そのため、その交点には 電子2のスペースが存在する。
交点の状態は Fig.5, 中間状態、Fig.6 の間を周期的に変化していると考えられる。
(Fig.7) 2つの ド・ブロイ波は "必ず" 互いに垂直になる必要がある。
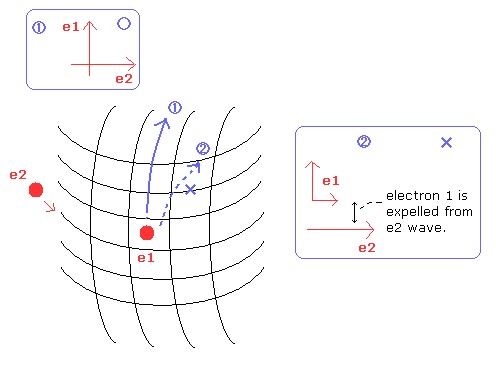
例えば、Davisson-Germer の干渉実験によれば、ド・ブロイ波の 幅は 少なくとも 0.091 nm (= 9100 MM ) 以上必要である。
なぜなら、その実験はニッケルの結晶を使っており、その間隔は d = 0.091 nm だからである。
トップページに示したように、我々の新しいボーアのヘリウム模型の半径は 約 3100 MM である。
このことは、ヘリウム原子においては、交点のみでなく すべての空間において 互いに垂直な ド・ブロイ波でなければならないことを意味する。
ヘリウムは小さい原子である。そのため もし 1つのド・ブロイ波の幅が ヘリウムの半径よりも小さいとすると、いろんな元素の結晶を用いた実際の実験において、我々は 電子の干渉を観察できないことになってしまう。
(Fig.8) Fig.4 の point 3 において、電子2の波は自身と打ち消し合う。
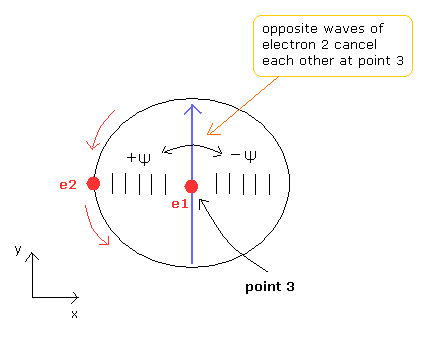
Fig.4 のヘリウム模型は 対称的な構造を持つため、Fig.4 の point 3 において、電子2のド・ブロイ波は自身と打ち消しあう。(Fig.8 参照)
結果として、電子1のド・ブロイ波は point 3 において、独立して安定さを保つことができる。
(Fig.9) 2つの軌道面は 90°以外の角度で交わることは可能か?
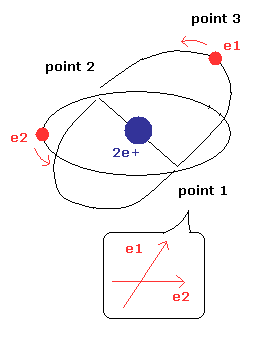
Fig.9 では、2つの軌道面は 90°以外の角度で交わっている。
しかしすでに述べたように、このケースは不可能である。なぜなら ヘリウム原子には 2つの電子が同じ方向に進むスペースがないからである。
Fig.9 の模型では、2つの軌道面とも原子核を含んでいる。
電子間の 反発力のため、2つの電子は避け合い、互いに平行になろうとする。
しかし すでに述べたように、この平行状態は Fig.2 や Fig.3 の状態を意味し、この状態では 1軌道に2つの電子を含んでいる。
(もちろん、これは不可能であり、実験結果とも一致しない。)
そのため、Fig.9 においては 電子2のド・ブロイ波による "壁" が クーロン反発力を ブロックする必要がある。
しかし、Fig.10A に示したように、Fig.9 の ド・ブロイ波の壁はとても不自然である。
(Fig.10) "不自然な" (= unnatural ) ド・ブロイ波の壁。
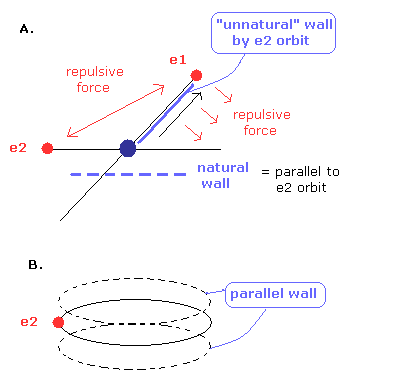
もし、ド・ブロイ波の ”壁” というものが存在するとしたら、Fig.10B に示すように その壁は 軌道に平行になる必要がある。
なぜなら、ド・ブロイ波は電子軌道から生成されるからである。
つまり 斜めの壁は不自然なのである。
(Fig.10-2) 電子が U ターンできない。
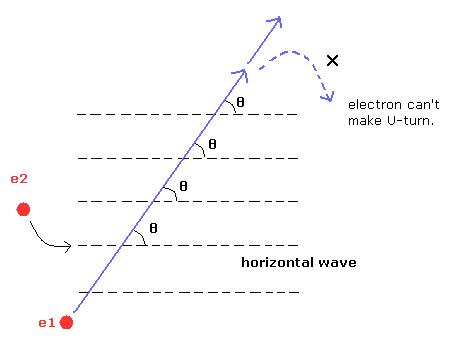
もし、電子1 (e1) と 電子2 (e2) のド・ブロイ波の間の角度が 90°以外の ある決まった値 (= θ) をとるとすると、電子は U ターンできなくなってしまう。
この状態では、電子はどこかへ飛び去ってしまう。
なぜなら、Fig.10-2 に示すように 電子が U ターンするためには この θ が ゼロになる必要があるからである。
もし、この角度 θ が 90°のとき、Fig.4 と Fig.8 に示すように 電子1 は point 3 を通って U ターンすることが可能である。
(Fig.11) 電子軌道が 不安定かつ不確定な状態。
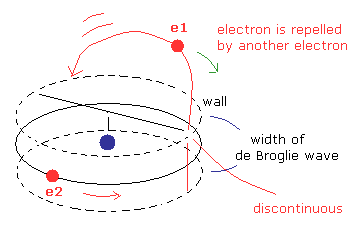
Fig.11 では、ド・ブロイ波の幅が とても狭いと仮定している。もちろんこれは Davisson-Germer などの干渉実験と一致しない。
Fig.11 のように ド・ブロイ波の壁が e2 軌道に平行とすると、e1 軌道は とても複雑かつ不安定なものになってしまう。
なぜなら Fig.11 に示すように もう1つの電子による影響が 壁の中と外の境界で 不連続 (= discontinupous ) なものになってしまうからである。
結果として、Fig.4 以外、安定なヘリウム模型というものは存在しないことになる。
トップページにおいて、我々は Fig.4 のヘリウム模型と サンプル JAVA プログラムを用いて 最も正確な基底状態のエネルギーを得ることに成功した。
(Fig.12) スタート地点 - 新しいボーアのヘリウム模型の 1/4 周の軌道。
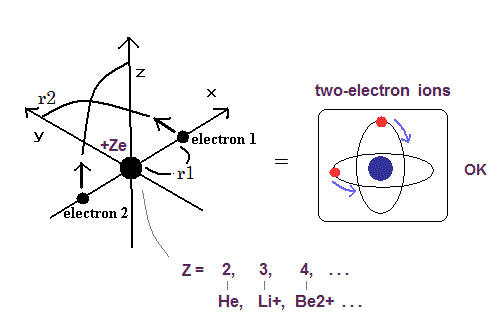
(Fig.13) 2つの電子が 1/4 周した時点。
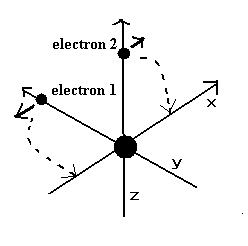
トップページでは、1 SS = 10-25 second という 新しい便利な単位を使用した。
しかし、この単位だと 計算に少し時間がかかってしまう (約1分)。
そこで、ここでは 1 SS = 10-23 second という単位にする。この単位だと、トップページとほぼ同じ結果を素早く だすことが可能である。
(Eq.1) 時間と長さの新しい単位。
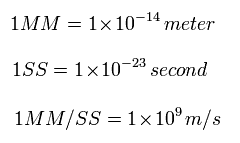
Eq.1 から 加速度の単位は、
(Eq.2)
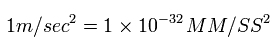
サンプル JAVA プログラム 1 SS = 1 × 10-23
サンプル C 言語 プログラム
(このプログラムにおいては、電子において通常の質量か 換算質量か選択することができる。)
上のソースプログラムをそのままテキストエディタ(メモ帳など)にコピー and ペースト すれば、簡単にコンパイルと実行できる。
(この class file name は remass なので、このテキストエディタを "remass.java" とセーブしてコンパイルしてほしい。)
このプログラムでは、最初に 換算質量の条件である 1 から 3 までの数を入力する。
"Normal" の条件 (= 1 ) では、重心が原点以外にあるとき 換算質量を用いる。
"NOT reduced mass" の条件 (= 2 ) では、必ず 通常の電子質量を用いる。
"All reduced mass" の条件 (= 3 ) では、重心が原点にあるときでさえ 必ず 換算質量を用いる。
次に 電子1の初期のx座標 r1 (MM) と ヘリウム の全エネルギー E の絶対値 (eV) を入力する。
入力された値から Fig.12 における 電子1の 初期速度を計算する。
"Normal" と "Not reduced mass" 条件では、Fig.12 においては 重心が原子核の地点にあるため 初期速度の計算のときに 通常の電子質量を使用する。
"All reduced mass" の条件では、この状況を無視して 初期速度の計算のときでさえも 換算質量を使用する。
そして、 1 SS ごとにプログラムが 2つの電子と1つの核の間のクーロン力を計算して軌道を修正していく。
対称性より、電子1が (xx, yy, 0) に位置するとき、電子2は (-xx, 0, yy) に位置する。( Fig.12 Fig.13 参照。)
MM から メートルへの変換は、x (m) = xx × 10-14。 y (m) = yy × 10-14である。
よって、電子1の x方向の加速度は(m/sec2) 次のようになる。
(Eq. 3) 加速度の x 成分。
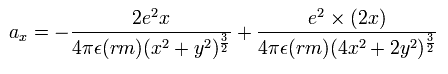
ここで、最初の項は核と電子1の間のクーロン力によるもので、2つめの項は2つの電子間のクーロン反発力によるものである。
ヘリウム原子核 (= α 粒子) の運動も考えて、我々はここで電子の換算質量 (rm =1/2 x (2me x nucleus)/(2me + nucleus) = 9.10688561 × 10-31 kg) を 核がちょうど2つの電子の中間にある場合を除いて使うことにする。
(Eq. 4) 電子の換算質量。
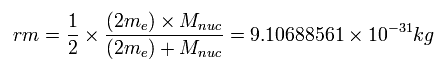
3体問題の換算質量も参照のこと。
"NOT reduced mass" 条件では これらの加速度や ド・ブロイ波の計算の際に 通常の電子質量を用いている。
同じく 電子1のy 方向の加速度は次のようになる。
(Eq. 5) 加速度の y 成分。
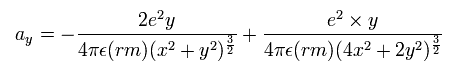
計算値に基づいて、電子の速度ベクトルと位置を変えていく。
電子1は X-Y平面のみを動くとしているため z方向の加速度は考えていない。
もし、電子にはたらく力のすべての成分を考慮すると、電子の運動は Fig.2 や Fig.3 に示すようになってしまう。
しかし、Fig.2 や Fig.3 では、2つの電子が1つの1ド・ブロイ波長のせまい円軌道におしこめられている。
そのため 2つの電子が入るスペースがない。
また、ここでは1 SS ごとに電子の速度からド・ブロイ波長を求め (λ = h/mv)ていく。
1 SS の間に電子が進む微小移動区間に含まれるド・ブロイ波 (1つの長さλ ) の数を次のように計算する(この合計が WN)。
(Eq. 6)
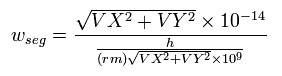
VX, VY は電子1の速度 (MM/SS) で、この式の分子は 1 SS に進む移動距離 (meter)、分母はド・ブロイ波の波長の長さ(meter)である。
両方ともメートルに変換するため少々複雑になっている。
ここでは、電子軌道をこのように100 万以上の微小区間 (1 SSごとに電子が進む微小移動距離)に分離している。
電子がその軌道の 1/4 進んで、その x 座標がゼロになったとき ( Fig.13 )、このプログラムはその地点での電子1の速度のy成分をチェックする (このy速度成分をを last VY とする)。
もし、last VY がゼロの時、2つの電子は Fig.12 と Fig.13 に示す軌道を定期的に周回することになる。
それで、-0.00001 < last VY < 0.00001 (MM/SS) を満たすときのみ、このプログラムは画面上に r1, VY, preVY (1SS 前のVY), (mid)WN (軌道の1/4に含まれるド・ブロイ波の総数)を表示する。
Table 1 は "Normal" の条件のときで last VY が最もゼロに近いときの結果である。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -78.9900 | 3075.0 | 0.250022 | 1.000088 |
| -79.0000 | 3074.0 | 0.250006 | 1.000024 |
| -79.0037 | 3074.0 | 0.250000 | 1.000000 |
| -79.0100 | 3074.0 | 0.249990 | 0.999960 |
| -79.0300 | 3073.0 | 0.249958 | 0.999832 |
Table 1. ヘリウムのさまざまな エネルギー準位における Fig.13 の 電子1の速度のy成分がゼロのときの r1 と WN (ド・ブロイ波の数) の結果。
WN × 4 は 軌道1周に含まれる ド・ブロイ波の数の総数。
この結果は エネルギーに対する相対論的な補正値が -79.005147 - (-79.0037) = -0.001447 eV であることを示している。
ヘリウムイオン (He+) の基底状態のエネルギーの理論値は 換算質量を用いて ボーア模型や シュレディンガー方程式から得ることが可能である。
この値は -54.41531 eV である。
また He+ の基底状態のエネルギーの実験値は -54.41776 eV (Nist) である。
そのため、He+ イオンにおける エネルギーの相対論的な補正値は -54.41776-(-54.41531) = -0.00245 eV となる。
水素原子 (H) の基底状態のエネルギーの理論値も 換算質量を用いて ボーア模型や シュレディンガー方程式から得ることが可能である。
この値は -13.5983 eV である。
また H の基底状態のエネルギーの実験値は -13.59844 eV (Nist) である。
そのため、H における エネルギーの相対論的な補正値は -13.59844-(-13.5983) = -0.00014 eV となる。
中性ヘリウムの電子速度は ヘリウムイオンよりも遅く、また 水素原子よりも速い。
そのため 中性ヘリウムにおける 相対論的な補正値は -0.00245 eV と -0.00014 eV の間になる必要がある。
上の計算結果は -0.001447 eV で 何とそれらのちょうど間にある。
Table 2 は "Not reduced mass の条件" のときの結果である。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0037 | 3075.0 | 0.250071 | 1.000284 |
| -79.0300 | 3074.0 | 0.250030 | 1.000120 |
| -79.0485 | 3073.5 | 0.250000 | 1.000000 |
| -79.0600 | 3073.0 | 0.249982 | 0.999928 |
| -79.0800 | 3072.0 | 0.249950 | 0.999800 |
Table 2 に示したように、もし 中性ヘリウム原子において 換算質量を用いなかったら 計算結果は -79.0485 eV となり、 これは 実験結果 (-79.005147 eV) と異なる。
(誤差は -79.0485 - (-79.005147) = -0.04335 eV である。 Table 1 の結果の 0.001447 eV と比較するといい。)
この結果は ヘリウムの正確な基底状態のエネルギーを得るには 換算質量を用いなければならないことを意味している。
Table 3 は "All reduced mass の条件" の結果である。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0037 | 3075.0 | 0.250037 | 1.000148 |
| -79.0200 | 3074.5 | 0.250011 | 1.000044 |
| -79.0268 | 3074.0 | 0.250000 | 1.000000 |
| -79.0300 | 3074.0 | 0.249995 | 0.999980 |
| -79.0500 | 3073.0 | 0.249963 | 0.999852 |
Table 3 に示すように、重心が原子核の地点にあるときでさえ 換算質量を必ず使用したとすると、計算結果は -79.0268 eV となり、これは 実験結果 (-79.005147 eV) と異なる。
(誤差は -79.0268 - (-79.005147) = -0.021653 eV である。 Table 1 の結果の 0.001447 eV と比較するといい。)
このページに示したように、換算質量が 最初の 運動エネルギーの計算のときも含めて いつも有効だとしたら、2つの電子は 水素原子のように 互いにくっついている必要がある。
(Fig.14) 2体系の水素原子。
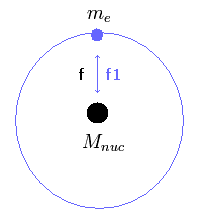
水素様原子では、電子の運動エネルギーに影響を与える力が 原子核の運動エネルギーに影響を与える力と ちょうど等しい。
しかし ヘリウムの2つの電子は 反発力のために互いにくっつくことはできない。
(Fig.15) ヘリウムの換算質量。
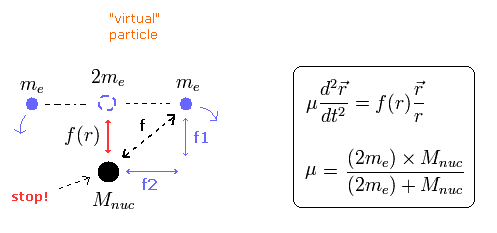
Fig.15 の 力 f2 は 電子の運動エネルギーのみに影響を与え, 原子核の運動エネルギーには 影響を与えない。
原子核の運動エネルギーは 力 f1 のみの影響を受ける。この f1 は 重心が原子核のところにあるときはゼロになる。
(もちろん 電子の運動エネルギーは 力 f1 と f2 の両方の影響を受ける。)
そのため、電子の運動エネルギー (速度) を計算するとき、我々は 水素原子のように 換算質量を用いることはできない。
この事実が Table 3 における 計算誤差を生じさせている。
(Fig.16) 中性ヘリウム原子における原子核の運動。
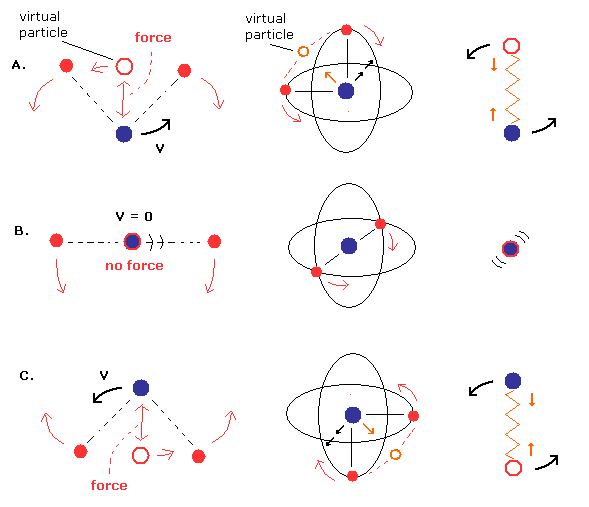
Fig.16 に示すように、原子核は 2つの電子の中心に仮定した"仮想"粒子との間の 引力によって 回転している。
2つの電子の中心が原子核に近づくにつれて、この引力は弱くなり 原子核の回転スピードが遅くなる。
Fig.16B は 重心が原子核と一致している状態である。
この状態では、原子核の回転速度はゼロであり、Fig.12 において 電子の初期速度の計算のさいには 換算質量ではなく 電子の通常質量を用いる必要がある。
Fig.16A と 16C において、原子核の回転速度は最大になる。
"仮想"粒子と原子核は 回転しながら互いに近づいていき そして離れていく。
Fig.16 は 原子核の”自然な”運動パターンである。
しかし Fig.17 に示すような 別の”特殊な”運動パターンを仮定することができる。
(Fig.17) 原子核が 回転のかわりに”振動”しているケース。 (= 特殊な場合。)
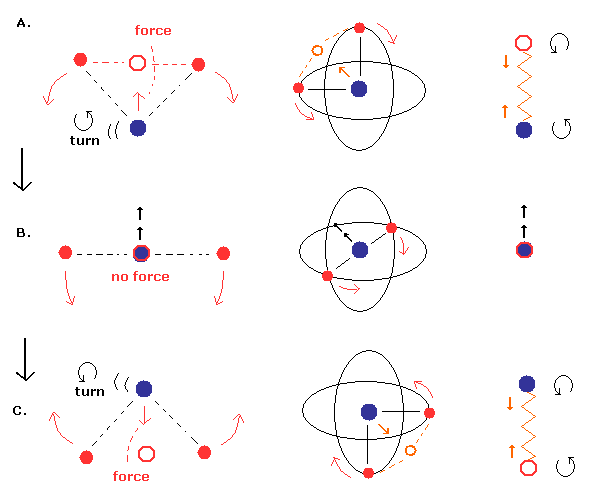
Fig.17 では、原子核はバネのように振動している。(= 線状の運動)
Fig.16 と異なり、原子核の速度 (回転ではなく) は 重心が原子核のところにあるときに 最大になる (Fig.17B)。
そして Fig.17A と Fig.17 C において、原子核の 向きが変わる。そのため その地点で 原子核の速度がゼロになる。
ところで、Fig.17 の運動パターンのエネルギーの結果は Fig.16 (= Table 1 ) と同じになるだろうか?
次に 運動パターンが Fig.17 のときの 中性ヘリウムの基底状態のエネルギーを計算してみることにする。
サンプル JAVA プログラム (= 原子核が Fig.17 のように振動している。)
サンプル C 言語 プログラム
下のソースプログラムをそのままテキストエディタ(メモ帳など)にコピー and ペースト すれば、簡単にコンパイルと実行できる。
(この class file name は perpen なので、このテキストエディタを "perpen.java" とセーブしてコンパイルしてほしい。)
このプログラムでは、最初に 電子1の初期の y座標 r2 (MM) (Fig.18 参照) と ヘリウム の全エネルギー E の絶対値 (eV) を入力する。
それらを入力すると、電子が、1/4 周した後の Fig.19 における電子1の速度の x成分 と、軌道 1/4 周に含まれるド・ブロイ波の数 ( midWN ) が画面に表示される。
(Fig.18) Fig.17 モデルの スタート地点。.
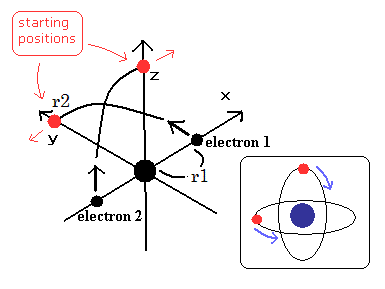
(Fig.19) 電子が 1/4 周した地点。
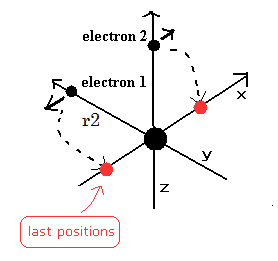
我々は Fig.18 の地点をスタート地点に選ぶ。
なぜなら Fig.17 の運動パターンでは、電子が Fig.17A と 17C の地点にあるとき ヘリウム原子核がストップするからである。
そのため Fig.18 の初期速度を計算するとき、換算質量でなく通常質量を使用する。
(スタート後は 換算質量を使う。)
Table 4 は Fig.17 の "原子核 振動モデル" の結果である。( last VX = 0 ).
| E (eV) | r2 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0000 | 3137.0 | 0.250011 | 1.000044 |
| -79.0037 | 3137.5 | 0.250005 | 1.000020 |
| -79.0069 | 3136.5 | 0.250000 | 1.000000 |
| -79.0100 | 3136.0 | 0.249996 | 0.999984 |
| -79.0300 | 3135.5 | 0.249964 | 0.999856 |
Table 4 に示すように、電子間の反発力のために r2 は r1 より少し長い。
また Table 4 の結果は -79.0069 eV で これは Table 1 の -79.0037 eV と少し違う。
もちろん この結果は Table 2 や Table 3 よりも正確である。
しかし Fig.17 (= Table 4) モデルでは 相対論的な補正値のみ説明することができない。
Fig.17 の 原子核振動モデルは 非常に "特殊"な場合であり、普通は起こりにくい。
例えば、互いに引き合う 惑星は 普通は 振動ではなく 回転する。
もし Fig.17 において スタート後もずっと 通常質量を用いたとすると、計算結果は -79.0485 eV となり、これは Table 2 (Not reduced mass consition) とまったく同じである。
また、Fig.17 において スタート地点においても 必ず 換算質量を用いたとすると、計算結果は -79.0268 eV となり、これは Table 3 (All reduced mass consition) とまったく同じである。
この結果は 質量関係を無視したとき、原子核の線状運動と回転運動を区別できないことを示している。
また、計算結果は Fig.16 (= Table 1 ) の原子核回転モデルが 正しいことを示している。
Fig.4 と Fig.7 に示すように、2つの電子が安定的にヘリウム原子核の周囲を運動するためには、2つの軌道は必ず 90o で交わっている必要がある。
もし この対称的な構造が 少しでも壊れると、このことは 2つの電子が運動できるスペースがなくなることを意味する。
2S 軌道 (= 2 ド・ブロイ波長) の半径は ボーア模型によれば、1S 軌道の 4倍長い。
そのため、もし 1S 軌道に 2つの電子のうち1つのみしか存在しないとすると、基底状態のエネルギーは 元の値よりも かなり高くなってしまう。
(Fig.20) 化合物の形成は "対称的な"構造の破壊を意味する。
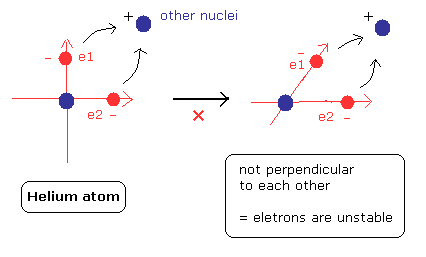
原子が他の元素と化合物を形成するとき、電子は他の正電荷の原子核に少し引きよせられる。
この構造の変化が いわゆる結合エネルギーを生じさせる。
しかし、Fig.20 に示すように、中性ヘリウムが他の元素と化合物を形成するとなると、2つの軌道の 直角の関係が壊れてしまう。
このことは、2つの電子のうちの1つが 1S 軌道から 2S 軌道に はじかれてしまう ことを意味する。
結果として 基底状態のエネルギーは 元の値よりも かなり高く (= 不安定) になってしまう。
そのため 他の元素 (もしくは ヘリウム自身) と結合する代わりに、中性ヘリウムは 対称的な構造を保つため "孤立した" 状態を選択するのである。
これが、今までに ヘリウムの化合物が見つかっていない理由である。
Fig.4 のヘリウム模型では、2つの軌道が 各ド・ブロイ波の位相を安定に保つため 互いに直角に交わっている。
他の角度では 各波の位相を独立に保つことはできない。
そのため、1S 状態には 3つ目の電子が入るスペースはもう存在しない。
このことは、Fig.4 のヘリウム模型によって パウリの排他原理を正確に説明できることを意味している。
ところで、互いに垂直に交わる軌道に 3つの電子を含むことは可能だろうか?
(Fig.21) 新しいリチウム原子 ? ( 3 × 1S 軌道 )
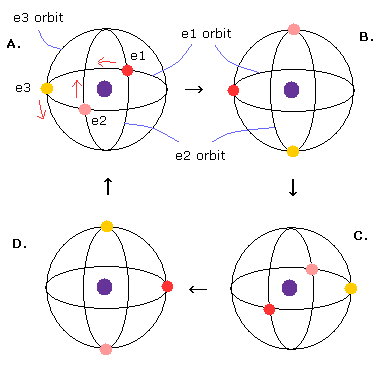
Fig.21 では 3つの 1S 軌道が 互いに垂直に交わっている。
このことは 1S 状態には 3つ目の電子が入るスペースがまだあるということだろうか?
(Fig.22) 3つの 1S 軌道では 長さが異なる。
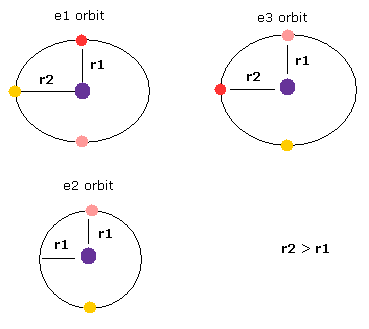
Fig.21 モデルを注意深く見てみると、e2 軌道のみが2つの電子を含んでいることに気づくだろう。(e1 と e3 は 3つの電子を含む。)
このことは、Fig.21 の 3つの軌道は Fig.22 に示すように 非対称であることを意味する。
そのため それらの電子の 時間周期が異なることになり、それは Fig.21 の運動パターンと一致しない。
(これは 安定な 閉じた軌道を壊してしまう。)
結果として、1S状態には 2つの”対称的な”軌道しか存在できないことになる。
水素原子と異なり、中性のヘリウム原子には磁気モーメントが存在しない。
標準のヘリウムでは、2つの電子は 反発力のため 互いに 離れて存在している。
そのため 理論的には スピンアップとダウンの状態は互いに完全には打ち消しあわないことになる。
(Fig.23) 磁気モーメントゼロ?
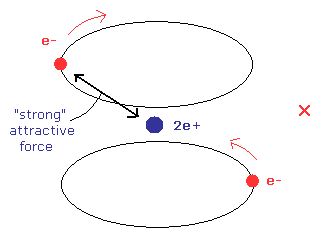
ヘリウムの磁気モーメントゼロを説明するため Fig.23 のヘリウムモデルを導入しようとする人たちがいる。
Fig.23 では、2つの電子は互いに平行な軌道上を 正反対の方向に運動している。
しかし、Fig.23 のモデルは 非常に不自然である。
2e+ の原子核と 電子の引力は 電子間の反発力よりもかなり大きい。
そのため Fig.24 のように 電子軌道面は原子核を中に含んでいる状態が普通である。
また 反発力のため、2つの軌道は 互いに完全には平行にならない。
(Fig.24) このモデルは パウリの排他原理と ゼロの磁気モーメントを説明可能である。
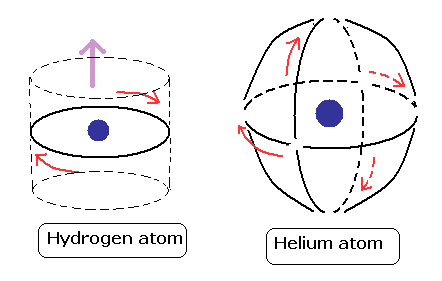
一方で、Fig.24 のヘリウム模型では、2つの軌道面がその中にヘリウム原子核を含んでいる。
また、これは パウリの排他原理と ゼロの磁気モーメントの現象を説明することが可能である。
(もちろん、この模型は それぞれのド・ブロイ波の位相が安定であることも説明できる。)

2011/7/24 updated This site is link free.