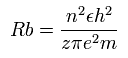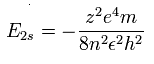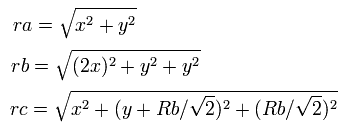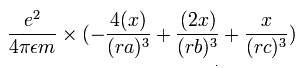トップページ (２電子原子も含む正確な新ボーア模型)
電子スピンは実在しない
我々の新しいボーア模型によって、ヘリウム原子の基底状態エネルギーの計算で、量子力学的な変分法よりも正確な結果をだすのに成功した。（トップページ参照のこと）。
この成功した新ボーア模型では、ヘリウム原子 (He) の２つの電子は、ちょうど１ド・ブロイ波長の互いに垂直な軌道上を運動している。
また、この新しい原子模型は、パウリの排他原理の現象も正確に説明できる。なぜなら、この新しいボーアの２電子原子には、３つめの電子が入りこむスペースがないからだ。
驚くべきことに、この新しいボーアのヘリウム構造は、他の２電子原子（イオン）である、リチウムイオン (Li+)、ベリリウムイオン (Be2+)、ホウ素イオン (B3+)、炭素イオン (C4+) にも正確にあてはめることができた。
（このページを参照のこと。）
さらに、３電子原子である、リチウム原子 (Li) のイオン化（基底状態の）エネルギーも、近似的なボーア模型の”２Ｓ”軌道を使用して、計算することができた。（このページも参照のこと。）
ここでは、、３電子原子である、ベリリウムイオン (Be+) に挑戦することにする。
ベリリウムイオン (Be+) は、１Ｓ軌道に２つの電子と、２Ｓ軌道に１つの電子をもっている。
１Ｓの２つの電子は、4e+ の原子核に強くひきつけられているため、2S の電子に比べてかなり原子核に距離的に近いところにある。
つまり、近似的に、我々は２Ｓ電子が、 +2e 原子核 (+4e - 2e = +2e) の周りの２ド・ブロイ波長の円軌道を回っているとみなすことができる。
（これは、我々が２Ｓ電子において、近似的に水素原子の式を使えることを意味する。）
ボーア模型によれば、n × ド・ブロイ波長の軌道の半径 (Rb) は、次のように なる。
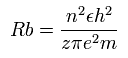
( z = 1 と n = 1 のとき、 Rb はいわゆる”ボーア半径”となる。)
Be+ の 2S 電子では、原子核の陽電荷 z は、2+ と近似的にみなすことができ（上を参照）、また、n は 2 である。
計算すると、この Rb は 2 × ボーア半径 ( = 1.0582 × 10-10 meter ( = 10583 MM ) となる。
（ここでは、便宜のため次のような新しい単位を使う。 1 MM = 10-14 meter, 1 SS = 10-22 second, 1 MM/SS = 108 m/s.）
水素様原子のエネルギー準位は、
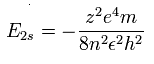
Be+ の 2S 電子では、n=2 と z=2 をこの式に代入する。
そのため、ベリリウムイオン (Be+) の原子模型をつぎのように仮定できる。
Fig. 1. ベリリウムイオン (Be+) 模型
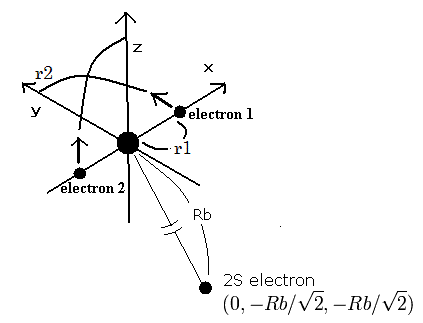
１Ｓの２つの電子はなるべく２Ｓ電子を避けるように運動する。そこで、我々は２Ｓ電子を Fig. 4. に示すように ( 0, - Rb / √2, - Rb / √2 ) に固定する。
(Fig.1 は３つの電子の相対的な位置関係を示している。実際は、この２Ｓの電子は１Ｓの電子よりもゆっくりと核の周りを周回している。)
Be2+ のように (このページを参照のこと)、電子１が、(x, y, 0) にあるとき、電子２は、 (-x, 0, y) にある。
つまり、各粒子間の距離は、
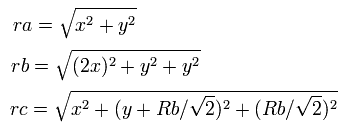
となる、ここで、ra は電子１と核の距離、rb は２つの 1S 電子間の距離、rc は電子１と 2S の電子の距離である。
電子１の加速度 (m/sec2) の ｘ成分は、
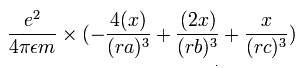
となる。
同様に、電子１の加速度 (m/sec2) の y成分は、
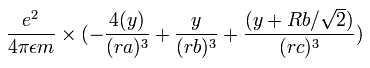
となる。
また、Be2+ のときのように、1S 軌道の 1/4 周に含まれるド・ブロイ波の数を計算する。
サンプルＪＡＶＡプログラム (Be+)
Table 1 は、Be+ において、 last VY （電子１が 1/4 周した後の速度の y 成分）がゼロに一番近い時の結果を示す。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -375.0 | 1482.5 | 0.25478 | 1.01948 |
| -380.0 | 1462.0 | 0.25302 | 1.01208 |
| -385.0 | 1442.0 | 0.25129 | 1.00516 |
| -388.82 | 1427.0 | 0.25000 | 1.00000 |
| -395.0 | 1403.5 | 0.24794 | 0.99176 |
| -400.0 | 1385.0 | 0.24632 | 0.98528 |
| -405.0 | 1367.0 | 0.24473 | 0.97892 |
この結果は、Be+ イオンの基底状態エネルギーが -388.82 eV のとき、軌道の長さがド・ブロイ波長の ちょうど 1.00000 倍になることを示している。
ベリリウムイオン (Be+) エネルギーの実験値は -18.21116 - 153.89661 - 217.71865 = -389.826 eV である。
つまり、計算誤差は、わずか 1.0 eV ( 0.25 % ) である。
(この小さな計算誤差は、おそらく、”近似的な”２Ｓ電子軌道を用いたことによると考えられる。)
このことは、ベリリウムイオン (Be+) の３つの電子が、 Fig.1 に示すように運動していると言ってほぼ間違いないということを意味する。
中性のベリリウム (Be) においては、２つの 2S 軌道の電子はどう動いているのだろうか？
ベリリウムは、４つの電子をもっており、そのうち、２つの 1S 軌道の電子は 原子核にとても近づいており （上の Be+ のセクションを参照のこと）、２つの 2S 軌道の電子は、原子核を挟んで反対側を運動していると考えられる。
2S の電子軌道は、円形というよりは、ほぼ 楕円形 と考えられる。
水素様原子のように、中心にたった一つの電荷があるときは、軌道は、楕円もしくは円形となる。
そして、Fig.2 に示すように、楕円の長軸と短軸は、互いにちょうど平行になれる。
Fig. 2. 水素様原子もしくは、非水素様原子の電子軌道
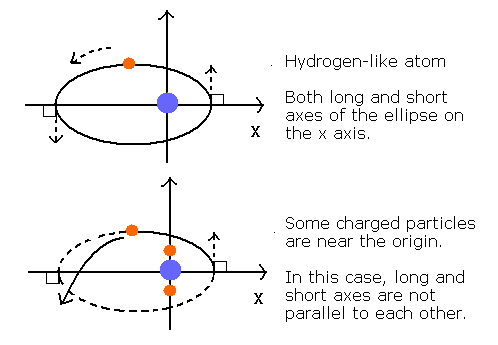
しかし、中心に電荷がいくつかあるときは（例えば、１つの原子核＋２つの 1S 電子）、軌道の長軸と短軸は一般的に、互いに平行にはならない。
そのため、軌道全体は、Fig.3 のように核の周囲を歳差運動することになる。
Fig. 3 推定されるベリリウム原子 (Be) 模型.
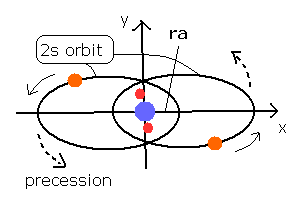
4e+ の原子核は原点にあり、1S 軌道の電子は、(0, 0, ± 1430 MM ) に（近似的に）位置させ、2S 軌道の電子１は、(ra, 0, 0) を出発し、X-Y 平面を運動するとする。
ここでは、次のサンプルＪＡＶＡプログラムを使用する。
サンプルＪＡＶＡプログラム (Be)
このサンプルプログラムでは、実行すると、まず、電子１の最初のｘ座標 ra (MM) を入力するように画面に表示される。
電子が軌道を１周して、ド・ブロイ波の数がちょうど２になったとき （この地点を電子１の last point とする。）、
このプログラムは次の値を画面に表示する。
last point の座標、速度、原子核との距離、速度と座標の内積 (= VXA*xxa + VYA*yya ),
また、電子１の軌道上の点の中で、最も核との距離が長く（もしくは短く）なるときの、その距離。
ra として、2286.40 MM (= 0.2286 × 10-10 meter) を入力したとき、原子核と last point の電子１の距離は、2286.66 となり、またそのときの、速度と座標の内積は、ゼロに近くなる。
これは、最初のｘ座標が 2286.40 MM のとき、電子がもとの状態 (距離は約 2286 MM) に戻れたことを意味する。
原子核と 2S 軌道の点の間の最も短い距離 (2286.40) は、最初の ra と同じであることがわかる。
また、最も長い距離は 15578.72 MM となる。
おそらく、本当のベリリウム (Be) の電子軌道はこのようになると推定される。
2010/7/30 updated This site is link free.