Top page (correct Bohr model including helium. )
Topological insulator is real ?
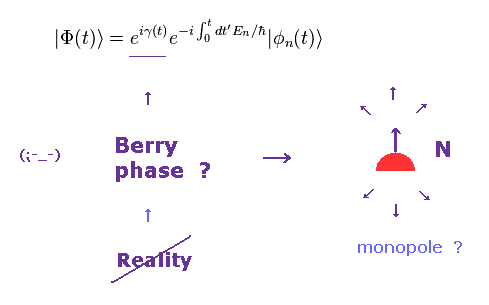
(Fig.1) What is Berry phase ? Monopole ?

In this section, we explain and derive Berry phase.
Time dependent Schrodinger equation is
(Eq.1)
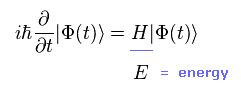
"H" is Hamiltonian.
Here we define new phase θ like
(Eq.2)
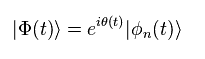
This is similar to gauge field of standard model.
"Gauge" is only mathematical concept, so it cannot appear openly.
But they consider this gauge is the most important. This is very strange.
Substituting Eq.2 into Eq.3,
(Eq.3)

As you see Eq.3, due to new phase of θ, this form becomes different from usual Schrodinger equation.
(Eq.3')
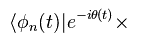
Multiplying Eq.3 by Eq.3' from the left side, we have
(Eq.4)

Integrating both sides of Eq.4 with respect to the time t,
(Eq.5)

Substituting θ of Eq.5 into Eq.2, we get the original wavefunction of
(Eq.6)
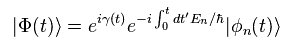
where
(Eq.7)
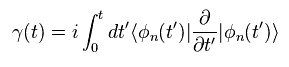
Here we define new arbitrary parameter R(t).
We suppose this R(t) changes periodically with time, and returns to the original value at the time interval of "t".
So we can express this equation as integral with respect to "R" instead of "t".
(Eq.8)
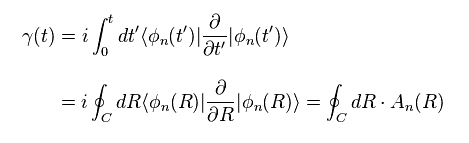
where
(Eq.9)
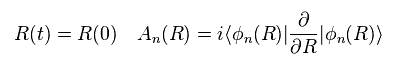
If we define like Eq.10, this relation is very similar to that between magnetic field B and vector potential A.
(Eq.10)
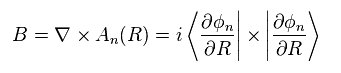
The γ(t) of Eq.8 is the line integral of vector potential, which corresponts to magnetic flux (= Φ ).
As you see, these vector potential "A" and magnetic field "B" are just "fake" ones.
From the relation of the curl of Eq.10, the z component of Berry curvature Bz becomes
(Eq.11)
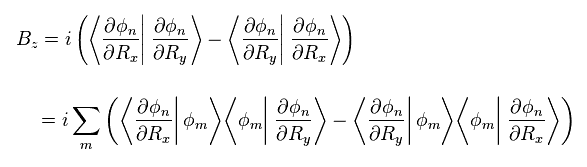
where other eigenfunctions φm are inserted.
(Eq.12)
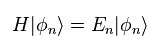
Eq.12 is Hamiltonitan and eigenfunction.
Partially differentiating Eq.12 with respect to parameter "R",
(Eq.13)
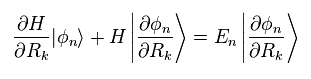
Multiplying Eq.13 by other φm from left hand side, ans using the following relation,
(Eq.14)
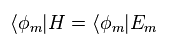
Eq.13 becomes
(Eq.15)

The complex conjugate of Eq.15 is
(Eq.16)

Substituting Eq.15 and Eq.16 into Eq.11, we have
(Eq.17)

In quantum Hall effect, we consider the 2-dimensional system under the electric field (= Ey ).
So this additional Hamiltonian is "eEyy".
As shown on this page, wavefunction of the first perturbation becomes
(Eq.18)

Using Eq.18, the electric current density (= j = -evxρ ) in the x direction becomes
(Eq.19)
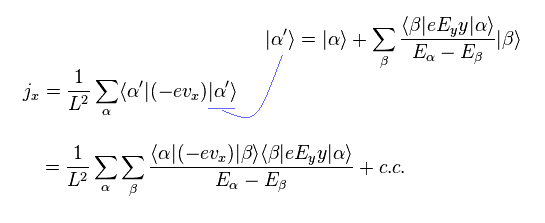
where "c.c" means "complex conjugate".
And we neglect the second order effect of this perturbation.
From Heisenberg commutation relation, we have
(Eq.20)
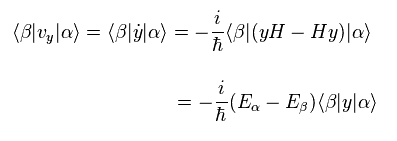
Substituting Eq.20 into Eq.19, we have
(Eq.21)
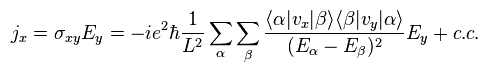
Using the following relation in Eq.21,
(Eq.22)
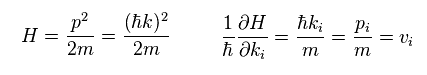
we can get the Hall conductunce of
(Eq.23)
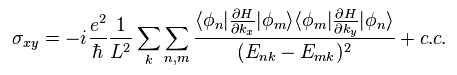
Using Eq.17,
(Eq.17)

Eq.23 becomes
(Eq.24)

where
(Eq.25)
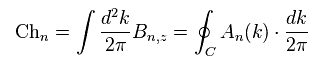
This (= "Ch" ) is called "Chern number".
When this Chern number is an integer, Hall cunductance of Eq.24 becomes quantized, they insist.
But as you see, these Berry phase has NO relation with this real world at all.
(Fig.2) Massless Dirac particle also in graphene ?

It is known that honeycomb lattice graphene also has massless Dirac fermions, as shown on this site and this site.
Again, this massless fermion is only mathematical concept with NO physical entity.
In this section, we explain this massless particle in graphene ( see also this section ).
(Eq.26) Graphene Hamiltonian
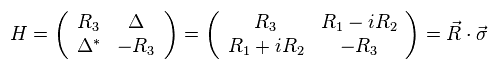
Like Dirac equation with no mass, Hamiltonian of graphene massless particle can be expressed in Eq.26.
Papameter "R" is proportional to wavenumber "k".
(Eq.27)
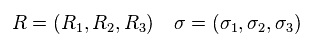
And σ is Pauli matrices.
Using Halmiltonian of Eq.26,
(Eq.28)
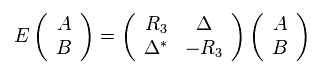
From Eq.28
(Eq.29)

To avoid the meaningless solution of A = B = 0, the following relation must be satisfied.
(Eq.30)
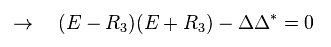
From Eq.26, Eq.30 becomes
(Eq.31)

As you see Eq.31, energy is linearly proportional to "R" (= wavenumber "k" ).
This is the reason why this equation is called massless (= photon-like ) Dirac fermion.
As shown on this page, usual Dirac equation with mass is
(Eq.32)

where γ is 4 × 4 matrices.
From Eq.32, Hamiltonian becomes
(Eq.33)
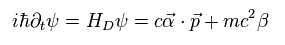
where
(Eq.34)

σ is 2×2 Pauli matrices.
From Eq.33 and Eq.34, you find Hamiltonian can be divided into 2 × 2 matrices, when the mass is zero.
(Eq.35)
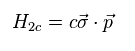
Eq.26 is based on Drac massless equation of Eq.35.
In 2-dimensional system, z compolent (= R3 ) of R is zero.
(Eq.36)
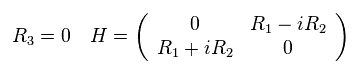
Here we define the following vector "s" using the unit vector ns.
(Eq.37)

Using the antisymmetric relation of Pauli matrices,
(Eq.38)
From Eq.36 and Eq.37, we have
(Eq.39)
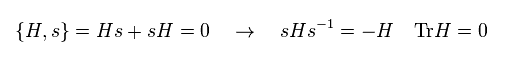
and
(Eq.40)

From Eq.40, you find the vectors R and n are perpendicular to each other.
This is called "chiral symmetry", they insist.
( Of course, it's only mathematical concept with NO physical meaning. )
Differentiating Hamiltonian of Ee.26, we have
(Eq.41)

where
(Eq.42)
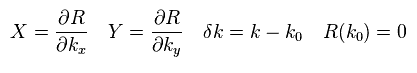
We suppose wavenumber R(k) becomes zero at the point k0.
There are two ±k0 points where the energy gap between conduction and valence bands is zero (= gapless ).
(Eq.43)
From Eq.42 and Eq.43, this Hamiltonian is massless ( photonlike ) form.
(Fig.3) Fractional QHE = fractional charge !?
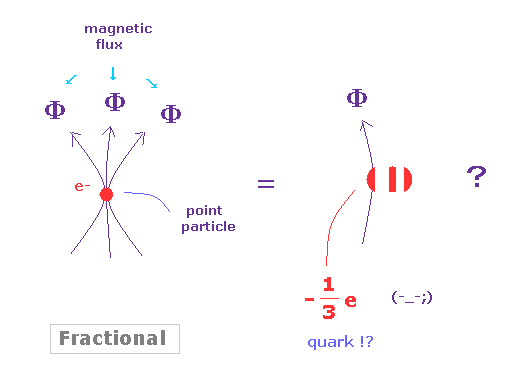
After discovering 1/3 fractional quantum Hall effect (= FQHE ), Laughlin proposed the first theory to explain this phenomena.
But as shown on this site, this theory depends too much on mathematical ( NOT physical ) concepts.
As shown in Fig.3, in fractional Hall effect, a point-like electron includes several magnetic flux in it.
This is completely impossible from the realistic viewpoint.
Furthermore, Laughlin theory cannot explain fractional QHE such as 1/2, which denominator is even number.
We define the external magnetic field B is in z direction.
So the vector potential A is
(Eq.44)
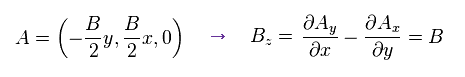
From Eq.44, Hamiltonian becomes
(Eq.45)

Here we define
(Eq.46)
Substituting Eq.44 and p = -iħ∇ into Eq.45, Hamiltonian becomes
(Eq.47)
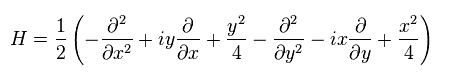
Here we define
(Eq.48)
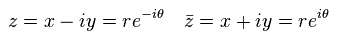
From Eq.48,
(Eq.49)
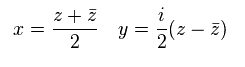
Using z of Eq.48, Hamiltonian of Eq.47 becomes
(Eq.50)
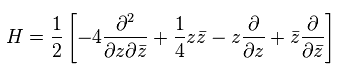
where we use
(Eq.51)

and
(Eq.52)
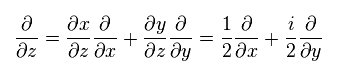
and
(Eq.53)
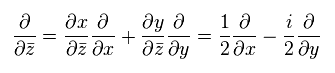
We introduce new creation and annihilation operators.
(Eq.54)
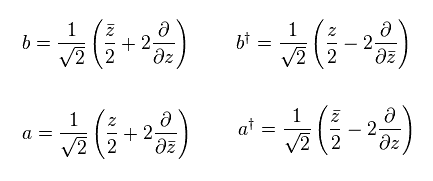
You find Eq.54 satisfy the commutation relation of
(Eq.55)

Hamiltonian of Eq.50 can be expressed using a†a operators of
(Eq.56)
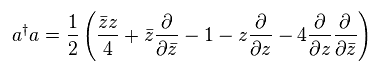
where we use
(Eq.57)
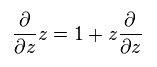
The orbital angular momentum operator (= L ) can be defined as
(Eq.58)

As shown in Eq.58, b†b and a†a number operators act in opposite way.
He took use of this thing.
(Eq.59)
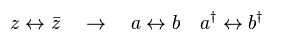
From Eq.54, you can exchange "a" and "b" by exhanging "z" and "bar-z".
By exchanging z and bar-z in Eq.56, you can get b†b.
Subsituting these values into Eq.58, we have
(Eq.60)
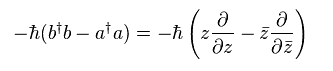
In Eq.60, only two terms are left.
( All other terms are cancelled out by subtraction.)
From Eq.48,
(Eq.61)
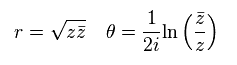
From Eq.61
(Eq.62)
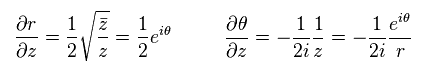
As a result,
(Eq.63)
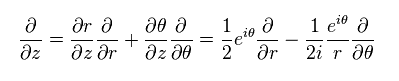
and
(Eq.64)
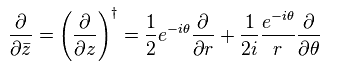
Using Eq.48, Eq.63 and Eq.64, Eq.60 becomes
(Eq.65)
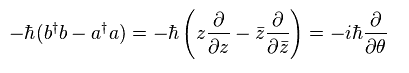
You find Eq.65 is angular momentum operators.
When eigenfunction has energy level "n" and angular momentum "l",
(Eq.66)
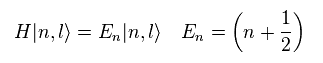
Considering Eq.65, we have
(Eq.67)
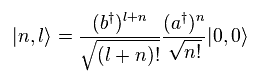
As you see Eq.65, "b†" operator increases only angular momentum.
On the other hand, "a†" operator increases energy, but decreases angular momentum.
(Eq.68)
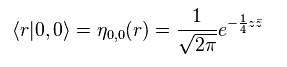
and
(Eq.69)
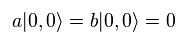
They suddenly suppose strange state where energy n = 0, but angular momentum l is NOT zero,
(Eq.70) Energy n = 0, but angular momentum l is NOT zero !
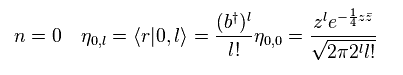
The state of Eq.70 is completely unrealistic.
It is natural that as angular momentum "l" increases, the energy "n" also increases.
This unreasonable misuse is caused by misunderstanding about the angular momentum operator of Eq.65.
In Eq.65, some terms of "b†b" must be cancelled out by "a†a" to get angular momentum operator.
So, when "a†a" = 0, angular momentum operator itself cannot be gotten.
(Eq.71)
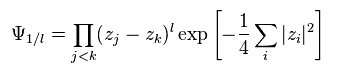
From Eq.54, creation operator b† becomes "z", when it acts on the vacuum.
And here they introduced antisymemtric variational function of Eq.71.
Strange to say, Eq.71 means the wavefunction with NO energy ( n = 0 ), but having several angular momentum !.
This unreal wavefunction leads to fractional Hall conductance of
(Eq.72)
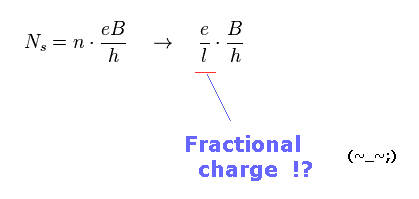
Strange composite quasiparticles appear in these phenomena, they insist.
As you see, the current quantum mechanics depend ONLY on fictitious fractional charges to describe fractional quantum Hall effect.
Tis is disaster.
(Fig.4) Spin and Dirac fermion (= massless ) of graphene are all "unreal".
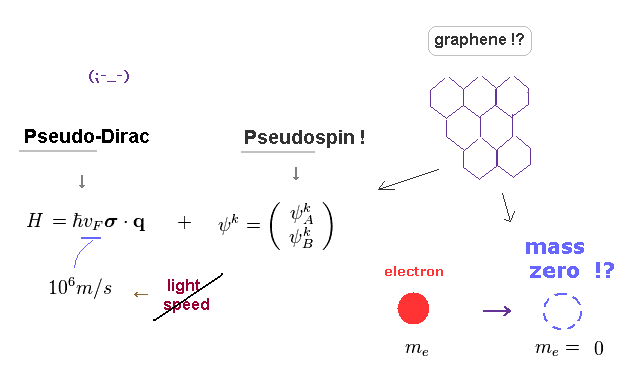
Graphene is a one atom thick layer of graphite, arranged in a "honeycomb" lattice.
Due to its high conductivity, they argue graphene includes massless Dirac fermion, which energy is "gapless" at some points.
Of course, this massless Dirac fermion (= electron ) is unreal quasiparticle.
Furthermore, massless Dirac ( Weyl ) equation in graphene is pseudo-equation.
As shown on this (p.8), this (p.5), this, this (p.4). the massless fermion is much slower ( v = 106 m/s ) than light speed "c" (= 3 × 108 m/s ) ! So it contradicts basic special relativity in which massless particle is always light-speed.
And the spin of this Dirac fermion is pseudo-spin (= unreal ), as shown on this (p.4) and this (p.16).
The current condensed matter physics just pursues illusory concepts, NOT investigating true machanism of atoms and spin.
(Fig.5) Three vectors (= δ = 1,2,3 ) in honeycomb graphene.

In this section, we derive massless Dirac equation in graphene, and shows this method is just math "trick" without physical meaning at all.
As shown in Fig.5, there are two sublattice of carbons A and B.
Considering regular hexagonal arrangement of atoms, three primitive vectors of Fig.5 become
(Eq.73)
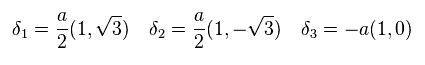
They introduced very abstract Hamiltonian (= Eq.74 ) of graphene.
"a" and "b" are ( annihilation ) operators of carbon atoms in A and B.
(Eq.74) Hamiltonian of graphene, "too simple" to be useful.
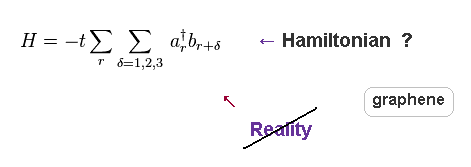
"t" is the nearest-neighbor hopping paramter ( 2.7 eV ), which has to be estimated empirically from experiments ( NOT by theory itself ).
As you see, you easily find this kind of very abstract equation has NO ability to describe dynamic and complicated motions of actual particles.
(Eq.75)
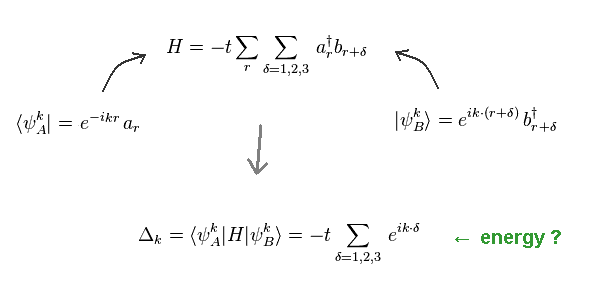
Adding proper eigenfunctions to the Hamiltonian of Eq.74 from both sides, we get the eigenvalue of energy in Eq.75.
Here we use the following anticommulation relation of fermions
(Eq.76)

Only the combinations of creation (= b† ) and annihilation (= "b" ) opearators with the same position (= r ) are left in "a" and "b" atoms.
Unfortunately, the present physicists try NOT to ask what force causes this Pauli exclusion principle.
They are just satisfied with these very abstract and unsubstantial relations, which attitudes hampers science progress.
(Eq.77)

Substituting Eq.73 into Eq.75, we get Eq.77.
Here we use
(Eq.78)
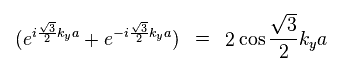
When the wavenumbers kx and ky are the following values, the energy (= Δ ) of Eq.77 becomes zero.
They call these points (in k space ) "Dirac point".
(Eq.79)
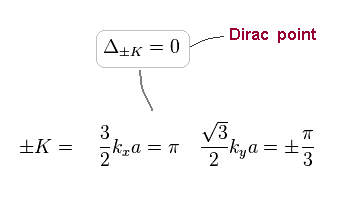
We think only about wavenumber (= k ) near K (= Dirac point ).
The difference between k and K is almost zero, so we consider only the first-order in Taylor series expansion of Eq.77.
(Eq.80) Taylor expansion and approximation (= 1st order ).

From Eq.80 and the definition of q = k - K, we obtain
(Eq.81)
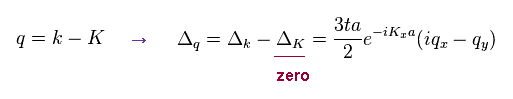
where qx = kx - Kx, and qy = ky - Ky.
In Eq.81, we can remove additional phase (= ieiKa ), so
(Eq.82)

Using the actual lattice constant (= a ) and the interaction energy (= 2.8 eV ), we find the velocity of this massless Dirac fermion is much lower than the light speed "c".
(Eq.83)

This means this Dirac ( Weyl ) equation used in graphene is just "fake".
The current physics tends to regard meaningless analogy and similar form as important, which logic resembles the rhyme of songs and poems rather than physics.
(Eq.84)
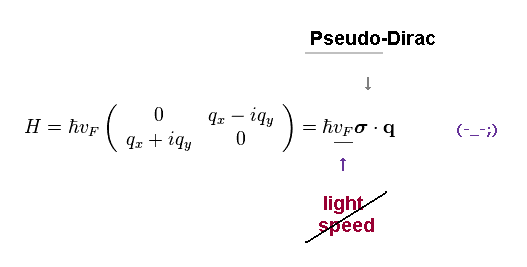
Pseudo (= fake )- Dirac equation means these methods have NO physical meaning.
The present physicists and journals are wasting a great deal of time in these fictitious concepts.
(Eq.85) σ = "artificial" Pauli matrices.
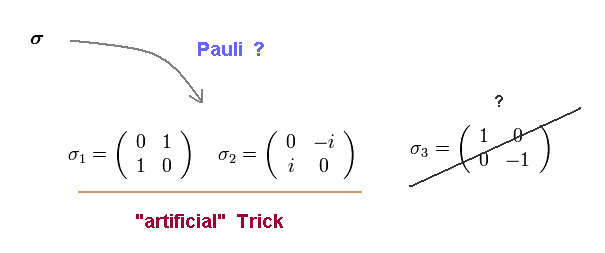
As you see Eq.84, it is obvious that they aimed at creating "artificial" Pauli matrices ( only σx and σy ) by force.
This is just mathematical trick, ignoring physical reality.
(Eq.86)

Furthermore, the eigenstates of Eq.84 is pseudo-spin, which means unreal, again.
This pseudo-spin consists of wavefunction of A and B carbon atoms ( NOT particle or antiparticle ).
They just call this state "pseudospin", only because their forms are similar to the original spinor, neglecting their physical validity.
This is NOT physics.

2014/3/20 updated. Feel free to link to this site.