Top page (correct Bohr model including the two-electron atoms)
Bohr model vs. Bell's inequality (CHSH-type)
In the experiments using the photon pair, the Bell inequality is said to be violated.
But in these experiments, the detection efficiency of photons is low (= "detection" loophole).
To eliminate this detection loophole, the various experiments using the ion pair such as Be+ and Yb+ were done.
It is generally said that these experiments have succeeded in violating Bell inequality even though the detection efficiency is high.
But the important point is that the ion-trap experiments are completely different from those of photon pair, though they use the common words "Bell inequality violation".
In the photon case, the emitted photon pair which has parallel polarization shows the so-called "entanglement" when we measure at the polarizer.
(But as shown in this page, we have succeeded in expressing Bell inequality violation by local realistic electromagnetic wave model naturally !)
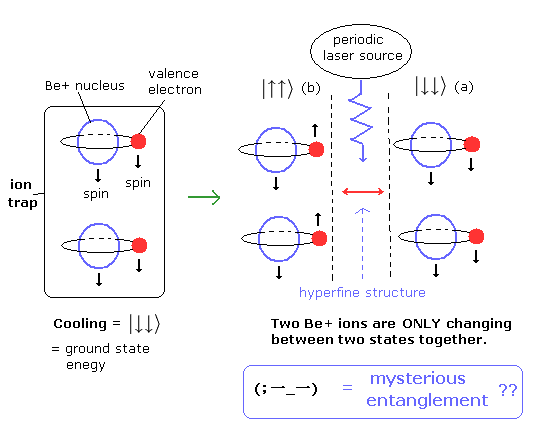
But in case of the ion pair (Nature 404, 256-259, 2000), they use the "artificial" ion (Paul) trap, which can continuously trap ions by the manipulated external electric fields.
And then, they only oscillate the ion pair simultaneously by the stable laser pulse source.
Fig.1. This really shows "mysterious" phenomenon of entanglement ??

In Fig.1, taking the beryllium ion (Be+) nuclear spin, they illuminate them Raman beams generated from laser sources.
The states of the ion pair are changing simultaneously between the two hyperfine structure levels (a and b) periodically, which can be achieved by changing beam radiation at the short time intervals.
The quantum physicists insist that these states mean surely "entanglement", though they are only periodically changing from the "classical" viewpoint.
(There are no "mysterious" things here.)
The quantum physicists hate the "real" motions such as oscillating, rotating, and changing.
Instead, they tend to use the word "superposition".
So the quantum mechanics trys to entangle us into the many-world like superposition states "intentionally", I think.
Fig.2. Oscillating vs. superposition.

From the viewpoint of this superposition (up and down mixed states in each Be+ ion = Eq.2), the same motions (= Eq.1) of these two ions mean the "mysterious" entanglement.
But actually, they are only changing simultaneously and periodically in the classical sense.
(Eq.1) Quantum physicists insist this is entanglement.

(Eq.2) Random superposition mixed states.
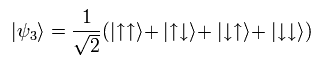
The important point is that these Be+ ions are NOT in superposition (= many worlds ) states.
Furthermore they don't show entanglement of these ions at all.
( See "Experimental violation of a Bell's inequality with efficient detection" )
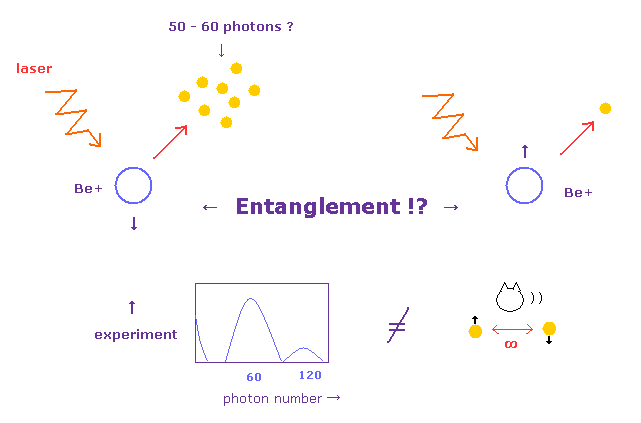
To know the hyperfine (= nuclear spin up or down ) state of each Be+ ion, they have to illuminate it by detection laser.
And they need to collect as many as 50 - 60 photon counts to determine its spin state.
So these experiment using ions are completely different from experiments based on two entangled photons.
Furthermore, they have to repeat these kinds of experiments to investigate Bell inequality violation.
In conclusion, the entanglement experiment using ion pair just shows classical mechanical statistics ( Not quantum spooky phenomena at all ).
(Fig.2') 50-60 photon counts are needed → these are NO entanglement.
Two beryllium (Be+) ions are confined along the axis of a linear Paul trap with an axial center of mass frequency of 5MHz. (Nature 409, 791-794, 2001).
(Paul trap is similar to Penning trap. About the Penning trap, see this page.)
The two ions are separated by a distance of approximately 3 μm.
The hyperfine structure is much smaller than the fine structure, and it results from the interaction between nuclear spin and the internally generated electric and magnetic fields such as electron spin (= Bohr magneton).
(Of course, also in Bohr model, the nuclear rotation (=spin) exists, which speed doesn't exceed the light speed due to its heavy mass.)
The hyperfine states of a trapped ion are commonly used for storing qubits in ion-trap quantum computing.
They have the advantage of having very long lifetimes.
A pair of laser pulses are used to drive the transition (of hyperfine structure), by having their frequency difference (detuning) equal to the required transition's frequency.
Be+ ion has -3/2 nuclear angular momentum, so the two resolved levels of the 2S1/2 ground state is as follows,
(but the nuclear magneton is much smaller than the Bohr magneton, so the nuclear magnetic moment is much smaller.)
(Eq.3) Down state of hyperfine structure.
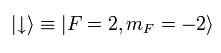
where F is the quantum number of the total angular momentum, and mF is the projection of the angular momentum along the quantization axis defined by an externally applied magnetic field.
(Here, the down state is mF = -3/2 - 1/2 = -2. See (a) of Fig.1. )
(Eq.4) Up state of hyperfine structure.
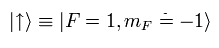
where mF = -3/2 + 1/2 = -1. See (b) of Fig.1.
In these experiments, they use the transitions between 2S1/2 and 2P1/2 (and 2S1/2 and 2P3/2) in the Be+ ion.
The common names such as 2S1/2, 2P1/2 and 2P3/2 are used also in the Be+ ion.
But actually, these states of Be+ are completely different things from those of the hydrogen atom !
(See Fig.3 or Phys. Rev A 31, 4, 2711-2714, 1985. )
Fig.3. Strange different energy levels in Be+, H and Na.
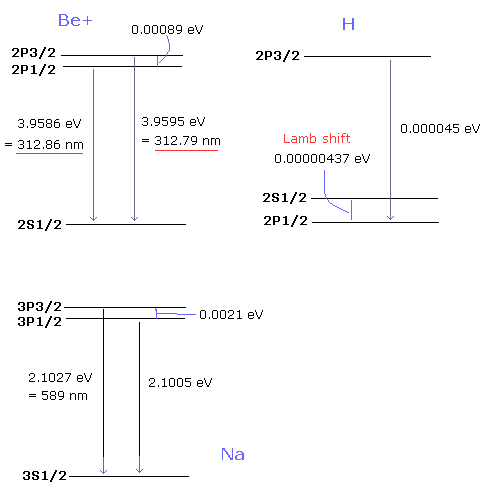
( 2.328 eV = 532.0 nm = 18794 cm-1 )
In the hydrogen atom, the energy levels of 2S1/2 and 2P1/2 are alomst same, and the very small energy difference between them are called "Lamb shift" (= 0.00000437 eV).
(See also Lamb shift is an illusion ?)
But in the Be+ ion and the sodium, these energy differences become much greater than that of the hydrogen !
( 0.00000437 eV (H) → 3.9586 eV (Be+) !)
The quantum physicists say that 2S (or 3S) electron penetrates past the shielding of the 1S electron, so the energy level of 2S (or 3S) is much lower than that of 2P (or 3P).
On the other hand, in the "delicate" anomalous Zeeman effect like the sodium, they don't consider the effects of the inner electrons at all ! (See this page)
So it is inconsistent.
And the energy level of 2S1/2 is a little higher than 2P1/2 in the hydrogen.
But in the Be+ ion and the sodium, 2P1/2 is much higher than 2S1/2.
Do you think the quantum physicists worry too much about the forms such as 2S1/2, 2P1/2, and 2P3/2 ?
It is natural that we distinguish the multi-electron atoms from the single-electron hydrogen.
For example, the time period of the outer shell electron's motion is different from that of the inner electron, because the outer shell electron is much slower than the inner ones.
At one time, the outer shell electron is a little closer to the inner electrons, and at another time, it is a little further away.
These different states may cause the small energy difference. (See also this page)
The two laser beams (R1, R2 of Fig.4) used to drive the transition have a wavelength of 313 nm (see Fig.3) and a difference frequency near the hyperfine splitting of the states (ω is about 2π × 1.25 GHz).
Fig.4. Energy levels of Be+ ion.
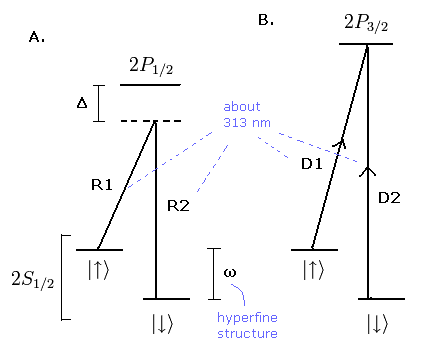
Here 2P1/2 is described in Fig.4, but this 2P1/2 doesn't appear in this experiment (= "virtual" state).
And this experiment seems to use near 313 nm laser in all transitions of R1, R2, D1, and D2 of Fig.4.
First they cool the Be+ ion, and make them the spin-down internal state, which means the ground state of their collective motion.
(See also Fig.1 or (a) of Fig.5.)
Fig.5. hyperfine levels of two Be+ ions.

Next, by applying optical fields oscillating at ω, the two-step transition from (a) to (b) in Fig.5 is driven.
The enegy differences of (c) in Fig.5 is small, so by driving the double transition for the appropriate time, the entanglement state of Eq.1 is created. (Nature 404, 256-259, 2000)
(They try to apply enough energy to excite the two (not only one) ions at the same time.)
(Eq.1) Entanglement state ?

Again, I think this state of Eq.1 is only oscillating "artificially", and NOT a "mysterious" entanglement state at all.
( How do you think about it ? )
We can confirm whether each Be+ ion is in the up (Eq.4) or down (Eq.3) states, by illuminating it with a circularly polarized laser beam (D1 or D2 of Fig.4).
The fluorescent brightness of it becomes different depending on the up or down states.
Next we investigate whether the Bell inequality is violated also in the Be+ ion. (Nature 409, 791-794, 2001.)
But different from the photon case, we have already got the answer of it, when we consider the Eq.1 as an entanglement state.
So we only express this state using Bell inequality (CHSH-type) formally.
In this paer, first they prepare a pair of Be+ ions in the entanglement state of Eq.1.
Second, a variable classical manipulation is applied independently to each particle.
These manipulations are labelled φ1 and φ2.
(In this experiment, the manipulation is a laser wave applied with phases φ1 and φ2 to ion 1 and ion 2, respectively.)
Finally, by applying the detection lasers, we measure the up (Eq.4) or down (Eq.3) Be+ ion states.
The correlation of these outcomes is
(Eq.5)
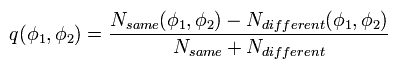
where Nsame and Ndifferent are the numbers of measurements where the two results were the same (= up,up + down,down) and different (= up,down + down,up), respectively.
In the photon case, these variables φ mean the angle of the light filter.
And instead of up or down of Be+ ion, the pass or reflect of the photon at the filter is measured.
( This page explain CHSH-type Bell inequality in detail. So see this page first. )
And they investigate whether the next Bell inequality is violated.
(Eq.6)

After making the entanglement state of Eq.1,
(Eq.1)

they again apply Raman beams for a pulse of short duration so that the state of each ion j (j=1 or 2) is transformed in the interaction picture as
(Eq.7) Manipulations.
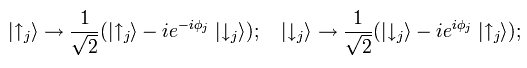
where the phase φj is the phase of the field driving the Raman transitions at the position of ion j.
These manipulation step of Eq,7 transforms the starting state of Eq.1 to
(Eq.8)
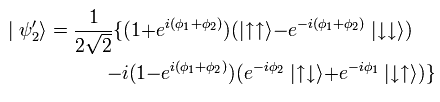
We can confirm Eq.8 by substituting Eq.7 into Eq.1.
Using the measurement operators of
(Eq.9)

and
(Eq.10)
 ,
,
the correlation function of Eq.5 is calculated to be
(Eq.11)
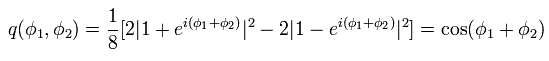 ,
,
The CHSH Bell inequality of Eq.6 is maximally violated at certain sets of phase angles.
One such set is
(Eq.12)
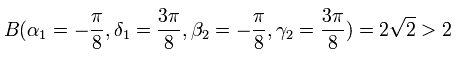
The experimental results of Eq.12 is B = 2.25, which is a little different from Eq.12.
But this violates the local realism condition, which requires that B < 2.
In the photon case, the instant the photon A passes the filter A, the polarization angle of the photon B becomes the same as the filter A (not filter B !) (=entanglemtnt).
(When the photon A reflects from the filter A, the polarization angle of the photon B becomes perpendicular to the filter A.)
These states (= same or perpendicular) after bumping into the filter correspond to Eq.1 of Be+ ions.
In the correlation function of Eq.11, we can express Eq.11 using only one variable φ (= φ1 + φ2).
This φ corresponds to the angle difference between the filter A and filter B in the photons.
Of course, if we substitute Eq.7 of the manipulation into the random superposition state of
(Eq.2)
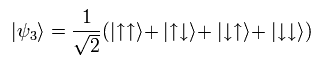
Bell inequality can not be violated.
But as I said above, the state of Eq.1 is "artificially" prepared.
Why can we claim that this state is a mysterious entanglement ?
Though it's just oscillating periodically from the classical viewpoint.

2011/4/2 updated. Feel free to link to this site.