Top page (correct Bohr model including the two-electron atoms)
In Bohr's three-electron atoms (ions), we calculate the energy of the 2S electron using the hydrogen-like atom's equation, which gives almost correct result.
Because we suppose that the inner 1S electrons are much closer to the nucleus than the 2S electron.
(For example, as shown in this Bohr's C3+ page, the central charge is supposed to be +4e =+6e -2e.)
But actually these inner 1S electrons are a little apart from the nucleus.
(In case of carbon, they are about 930 MM (1 MM = 10-14 meter) apart from the nucleus.)
So if we consider that the "effective" positive central charge is a little bigger (in the carbon atom, +4.25e instead of +4.0e), we can compute the valence electrons' motions correctly.
What is the difference between the upper C3+ and the neutral carbon cases ?
Here we use the carbon ion (C3+) as the representative of the three-electron atoms (ions).
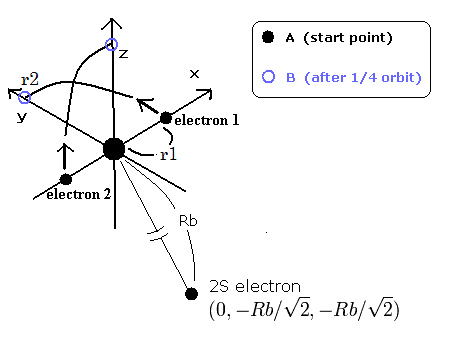
Fig.1. Three electron atoms (ions). C3+, Li, Be+, B2+ ....

As shown in this Bohr's C3+ page, we use the hydrogen-like energy equation at the starting point of Fig.1.
By the way, at the starting point (=A) and the point after 1/4 obiting (=B), what are the "effective" central positive charges which influence the 2S electron ?
Fig.2. Change of "effective" central positive charge.
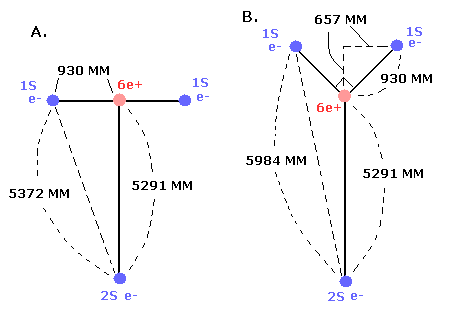
In the case of C3+, we suppose the distance between the nucleus and 2S electron is 5291 MM. (See this page.)
(And the distance between the 6e+ carbon nucleus and the 1S electrons proved to be about 930 MM.)
So at the starting point (=A), the "effective" central positive charge which influences the 2S electron becomes,
(For comparison, we calculate the potential energy (V) between the 2S electron and other particles.)
Eq.1. "Effective" central positive charge at start point (A).

As shown in Eq.1, if we consider that the two 1S electrons are a little apart from the 6e+ nucleus, the "effective " positive charge becomes a little bigger (+4.030) than +4e in the potential energy V.
And if the "effective" central positive charge is a little bigger, the radius becomes a little shorter, as follows,
Eq.2. Radius when the central positive chage is "z".
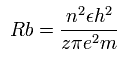
So the energy becomes much lower in proportion to z × z, as follows,
Eq.3. Energy when the central positive chage is "z".
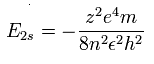
As a result, the true "effective" central positive charge at the starting point (=A) becomes +4.06 as follows,
Eq.4. True "effective" central positive chage at start point (A).

If we use this +4.06 instead of +4.0, the energy change becomes, (using the the 2S ionization energy (= 64.49 eV) of C3+ ),
Eq.5. Energy change at start point (A).
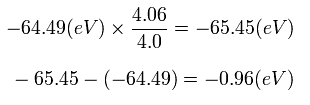
So the energy change is only 0.96 eV, if we consider that the 1S electrons are a little apart from the nucleus at the start point (A).
(Of course, in the lithium atom, this error becomes smaller, because the distance between 2S electron and nucleus is longer than C3+. )
How about the point after 1/4 orbiting (B of Fig.1 and 2) ?
At this point B, the "effective" central charge in the potential energy (V) becomes, (see Fig.2)
Eq.6. "Effective" central positive cahrge at 1/4 point (B).
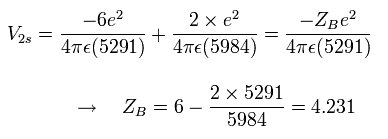
So the "effective" charge becomes +4.231e instead of +4.0e at the point B
Furthermore we need to consider the effect of the shortened radius (Eq.2 and Eq.3).
Eq.7. True "effective" central positive cahrge at 1/4 point (B).
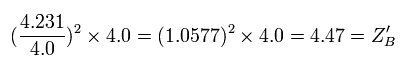
As a result, the true "effective" charge becomes +4.47e at the 1/4 point (B).
In the carbon ion (C3+) case, we use the hydrogen-like equations at the starting point (A).
So the error by this approximate methods is very small as shown in Eq.5.
This is the reason why we can get almost correct results in the three-electron atoms (ions) of Bohr model.
(The calculation result is -944.7 eV. The experimental value is -946.574 eV in C3+.)
After that, the two 1S electrons are moving around the nucleus avoiding the 2S electron (Fig.1).
On the other hand, in the neutral carbon, we need to consider 2S electron's "overall" motion instead of 1S electron.
So we have to avaerage the "effective" central positive charge.
(In the neutral carbon, we use the +4.25e instead of +4.0e, which value is between the above +4.47e and +4.06e.)
This is the reason why we can get the correct results also in the neutral carbon case.
------------------------------------------------------------
We have succeeded in calculating the ground state energies of the various three-electron atoms (ions) using the hydrogen-like atom's equations, as I said above.
By the way, how long does the 2S electron move its orbit, while the 1S electron moves one-quarter of its orbit ?
The total energy of 2 × 1S electrons in C3+ is -392.087 (5th ionization energy) -489.993 (6th) = -882.08 eV
And the total energy of 2S electron in C3+ is -64.49 eV (4th)
According to Virial theorem, the kinetic energy (T) and the total energy (E) satysfy T = - E.
So the ratio of 1S electron's velocity to 2S electron's velocity is,
Eq.8. Ratio of 1S electron's velocity to 2S electron. (C3+)
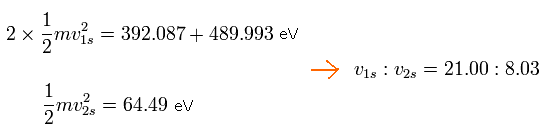
As I said above, the average radius of 1S orbit in C3+ is 930 MM. (one orbit = 2π × 930).
While the 1S electron moves one quarter of its orbit, the 2S electron moves 558.58 MM, as follows,
Eq.9. The moving distance (MM) of 2S electron while 1S electron moves 1/4 orbit.

The average radius of 2S electron is 5291 MM, which means one round of 2S orbit is 33243.35 MM, as follows,
Eq.10
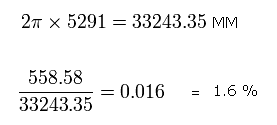
So the moving distance (= 558.58 MM) of the 2S electron during this time ( = 1/4 1S's orbit) is only 1.6 % of 2S orbit.
This result shows that we can fix 2S electron's position approximately as shown in Fig.1 when we calculate the three-electron atom's (ion's) orbit.
And this is also one of the reasons why we can get alomost correct results in the three-electron atoms (ions).
The orbital periods of the 1S and 2S electrons are different.
So the Rb of Fig.1 can be shorter than 5291 MM at the starting point.
But in this case, we need to change the hydrogen-like energy equation of Eq.3 a little.
For example, when we consider the "overall" motion of 2S electron, we have to condense three particles (= 2 × 1S electrons and 6e+ nucleus) into one point particle, approximately.
(It is very difficult to calculate the 2S electron's motion keeping those three particles separated.)
When the two 1S electrons are separated from the 6e+ nucleus, the "effective" central charge which influences 2S electron changes.
We can estimate this central charge by calculating the change of the potential energies (V).
But as shown in Fig.3, even when the distance between 2S electron and the central charge becomes shorter and the central charge of 4.0e+ doesn't change, the potential energy becomes lower.
Of course, in Fig.3 the central charge doesn't change. (It keeps 4.0e+.)
How can we exclude this case of Fig.3 ?
Fig.3. 4.0e+ charge doesn't change, but the potential energy becomes lower.
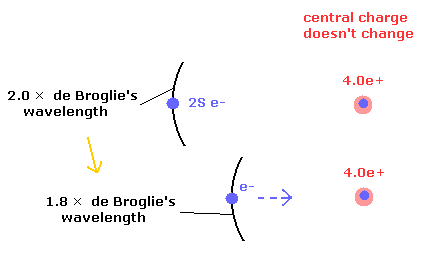
In Fig.3, the number of de Broglie's waves contained in one 2S orbit becomes less than 2.0.
So we can discriminate between these states from the viewpoint of de Broglie's waves, approximately.
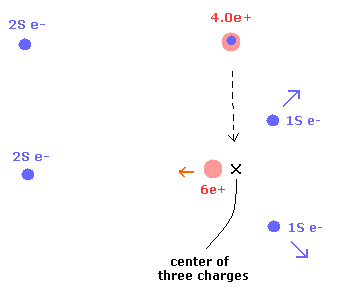
When the two 1S electrons are separated from 6e+ nucleus, they go away from the 2S electron.
On the other hand, 6e+ nucleus comes closer to the 2S electron.
As a result, the center of the three charges (= 2× 1S electrons + nucleus ) doesn't change. (Fig.4)
Fig.4. 1S electrons are repelled by, and the 6e+ nucleus are attracted to 2S electron.
In Fig. 2 (Eq.1 and Eq.6), the 2S electron and 6e+ nucleus don't move, and only 1S electrons go away from 2S electron.
So in the states of Fig.2 (Eq.1 and Eq.6), the center of three charges moves in the opposite direction from 2S electron a little.
Also in Eq.1 (Fig.2 A), due to the 1S electrons' separation, the center of three charges moves a little in the opposite direction from 2S electron. = The three charges spread into space.
(Here, we have to consider the effect of 1/r in the Coulomb relation in addition to these particles' coordinate.)
So we need to return the center of three charges to its original position.
Using Eq.2, which can adjust this position from the viewpoint of de Broglie's waves , we moves 2S electron a little closer to the nucleus as the 1S electrons go further away.
As a result, the "effective" distance between the center of three charges and 2S electron doesn't change.
And we can "concentrate" on the truely increased "effective" central charge.
Fig.5. Point-particle including the "separated particles" effects.
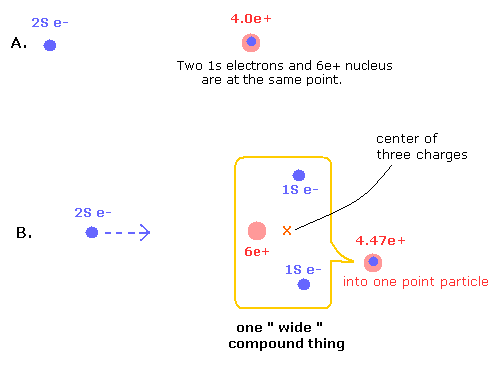
In the state of Fig.5 B, 1S electrons are avoiding 2S electron, and instead, 2S electron comes closer to the nucleus, which state is the same as the Fig.4 lower panel (= in Fig.4, 6e+ nucleus comes closer to 2S electron instead).
(This point-like nucleus is different from a wide compound thing which includes the particles which are separated in space.)
Here we use the potential energy change from the state in which three particles are at the same point (A of Fig.5) into the separated state (B).
And finally, we have to consider this wide compound thing as one point-like particle. ( + average A and B of Fig. 1,2)
The charge of this compound point particle is increased as compensation for this condensation in B.

2011/1/9 updated. Feel free to link to this site.