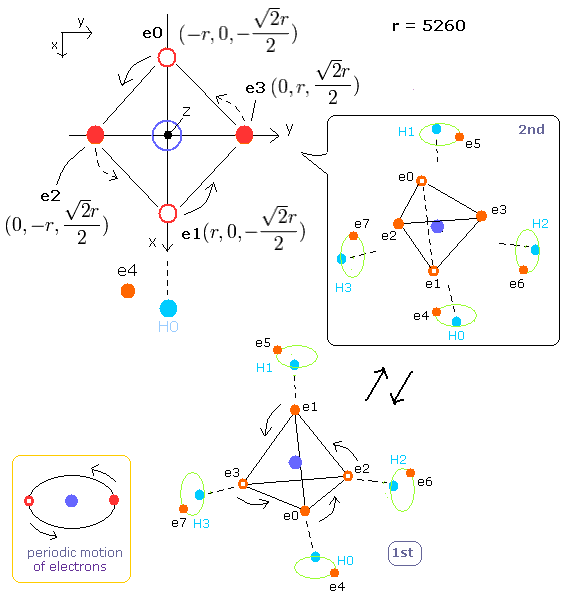
Top page (correct Bohr model including the two-electron atoms).
Electron spin is an illusion !
Our new Bohr model has succeeded in calculating the Helium ionization energy more correctly than the quantum mechanical variational methods as shown in the Top page.
In this new successful Bohr model, the two electrons of the helium atom (He) are moving on the orbits of just one de Broglie's wavelength, which are perpendicular to each other.
Furthermore, we have succeeded in visualizing the four valence electrons of carbon , and six valence electrons of oxygen.
(See Carbon page and Oxygen page).
In this page (Virial theorem of methane), we have succeeded in expressing the methane molecule by new Bohr model.
When we consider the C-C bond, we need to use the second version of methane (CH4) molecule, too.
Fig. 1. Periodic motions of methane's electrons

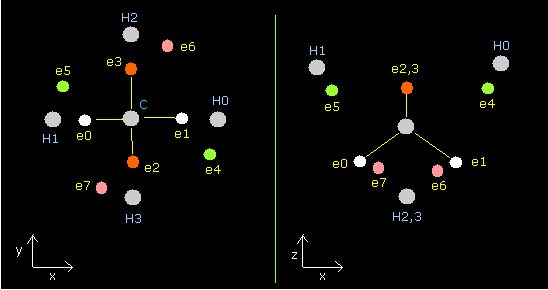
As shown in this Carbon page, there are two versions when the four valence electrons of carbon atom are arranged "tetrahedrally".
1st version --- the four electrons of carbon are the closest to each hydrogen's nucleus.
2nd version --- the four electrons move to the opposite positions of the carbon nucleus from the original positions.
Of course, the ground state energies of the 1st and 2nd versions of methane are the same (= -219.675 eV).
In the 1st version of methane, the hydrogens' electrons are repelled outward by the carbon's electrons.
In the 2nd version, the hydrogens' electrons become closer to the carbon nucleus, because the carbon's electrons go away from the hydrogen nuclei.
(On the other hand, the oxygen atom has only one version of "octahedral" structure.)
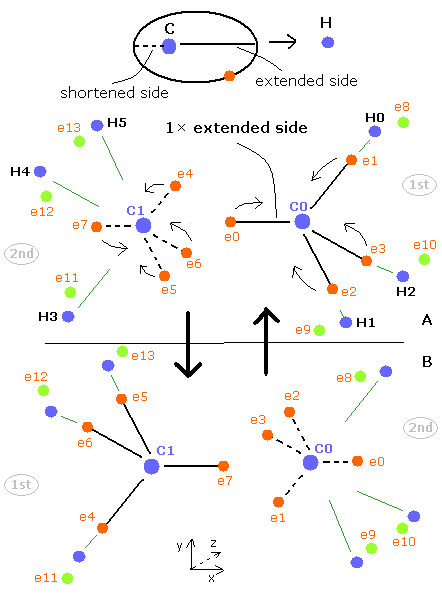
Here we try to express this 2nd version of methane using the next sample JAVA program.
Sample JAVA program of CH4 (second version)
If you copy and paste the program source code inside into a text editor, you can easily compile and run this.
(Unit of force: 1000 = force between +e nucleus and -e electron which are Bohr radius apart.)
According to the Virial theorem, the total potential energy (tV) of methane is -219.675 × 2 = -439.3 eV
When the total potential energy is about -439.3 eV, how are the eight electrons of methane arranged ?
About the detailed methods, see this page.
Fig. 2. The 2nd version of methane's (CH4) electrons
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -5260 | 0 | -3719 | 6442 | 2107 | 0 | -12 | 0 | 2.007 |
| ele 1 | 5260 | 0 | -3719 | 6442 | 2107 | 0 | 12 | 0 | 2.007 |
| ele 2 | 0 | -5260 | 3719 | 6442 | 2107 | 12 | 0 | 0 | 2.007 |
| ele 3 | 0 | 5260 | 3719 | 6442 | 2107 | -12 | 0 | 0 | 2.007 |
| ele 4 | -838 | -3530 | -2000 | 4142 | 1574 | 328 | 6 | 208 | 1.000 |
| ele 5 | 837 | 3530 | -2000 | 4142 | 1574 | -328 | -6 | 208 | 1.000 |
| ele 6 | 3530 | -838 | 2000 | 4142 | 1574 | -6 | 328 | -208 | 1.000 |
| ele 7 | -3530 | 837 | 2000 | 4142 | 1574 | 6 | -328 | -208 | 1.000 |
As shown in Table 1, the hydrogen electrons 4-7 are attracted to each hydrogen nucleus.
So, the hydrogen nuclei are attracted to these electrons, too. (Cn is big.)
As shown in this page, the distance between electron (4-7) and each hydrogen nucleus of the 1st version methane is 4896 MM.
So the average distance (nuc) is ( 4896 + 4142 ) / 2 = 4519 MM (about 4500 MM).
We can know the electron distribution of the 2nd version of methane.
Breaking all bonds ( 6 × C-H + C-C ) of ethane requires 2826.1 kJ/mol (= 29.29 eV)
So the ground state energy of ethane (8 carbon valence electrons + 6 hydrogen atoms) becomes -29.29 -148.024 × 2 -13.606 × 6 = -406.974 eV
(148.024 eV is the sum of 1-4th ionization energies of the carbon atom. )
According to the Virial theorem, the total potential energy (tV) becomes 2 × -406.974 = -813.948 eV.
The C-C and C-H bond lengths are 15351 MM, and 10940 MM, respectively. (1 MM = 10-14 meter).
And C-C-H angle is 111.7 degrees.
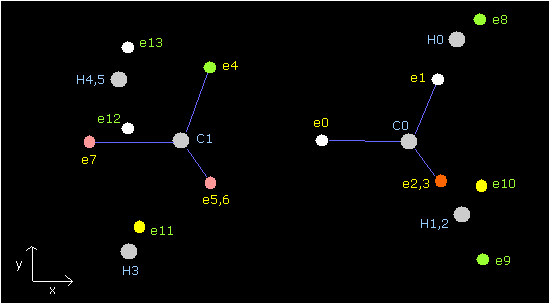
Fig. 3. Periodic motions of ethane's electrons (H3C-CH3)
As shown in Fig.3, the ethane molecule consists of a pair of the 1st and 2nd versions of methane.
Between two carbon nuclei, the four electrons are attracted by another nucleus avoiding each other.
Basically, each orbit of the electron is extended by the positive nuclei such as hydrogen and another carbon.
But here we are using the Virial theorem, so the both sides of each electron's orbit becomes the average length.
Here we try to express the ethane molecule using the next sample JAVA program.
About the detailed methods, see this page.
Sample JAVA program of ethane (Virial theorem)
(If you copy and paste the program source code inside into a text editor, you can easily compile and run this.)
In this program, the central charge (+4e = +6e -2e ) is supposed to be +4.217.
So de Broglie's wave is just 2.000, if the "tetrahedral" structure of carbon is completely kept.
Fig. 4. distribution of ethane's electrons (H3C-CH3)
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6285 | 0 | 0 | 6285 | 1880 | 0 | 0 | 0 | 2.006 |
| ele 1 | 2305 | 6019 | 0 | 6445 | 1267 | -6 | 2 | 0 | 1.995 |
| ele 4 | 2235 | 6045 | 0 | 6444 | 2064 | 33 | -6 | -43 | 1.999 |
| ele 5 | 2235 | -3022 | -5235 | 6444 | 2064 | 33 | -34 | 27 | 1.999 |
| ele 6 | 2235 | -3022 | 5235 | 6444 | 2064 | 33 | 40 | 16 | 1.999 |
| ele 7 | -6360 | 0 | 0 | 6360 | 2116 | 0 | 0 | 0 | 2.006 |
| ele 8 | 1800 | 1825 | -3705 | 4505 | 1017 | -247 | -614 | -2 | 1.000 |
| ele 10 | 1800 | 2296 | 3432 | 4505 | 1017 | -247 | 309 | -530 | 1.000 |
| ele 11 | 800 | 1975 | 3900 | 4444 | 1416 | -172 | -298 | 0 | 1.000 |
In Table 2, the total potential energy becomes -813.37 eV, which is almost same as the experimental value -813.948eV.
The average distance between electron (8-13) and each hydrogen nucleus is (4505 + 4444) / 2 = 4474.5 MM, which is almost 4500 MM.
Due to the repulsive force of another carbon, the "tetrahedral" structures of carbons are a little broken.
de Broglie's waves are a little different from 2.000. (The error is ± 0.005 (or 0.006))
Next we choose the value 16500 in the scrollbar and click the C-C (MM) button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6300 | 0 | 0 | 6300 | 2049 | 0 | 0 | 0 | 2.010 |
| ele 1 | 2315 | 6020 | 0 | 6449 | 1261 | -8 | 3 | 0 | 1.995 |
| ele 4 | 2290 | 6050 | 0 | 6468 | 2082 | 25 | -4 | -42 | 2.000 |
| ele 5 | 2290 | -3025 | -5239 | 6468 | 2082 | 25 | -34 | 25 | 2.000 |
| ele 6 | 2290 | -3024 | 5239 | 6468 | 2082 | 25 | 39 | 17 | 2.000 |
| ele 7 | -6380 | 0 | 0 | 6380 | 2119 | 0 | 0 | 0 | 2.016 |
| ele 8 | 1900 | 1600 | -3750 | 4498 | 1042 | -233 | -567 | -3 | 1.000 |
| ele 10 | 1900 | 2447 | 3260 | 4498 | 1042 | -233 | 287 | -489 | 1.000 |
| ele 11 | 800 | 1876 | 4110 | 4588 | 1358 | -158 | -234 | 1 | 1.000 |
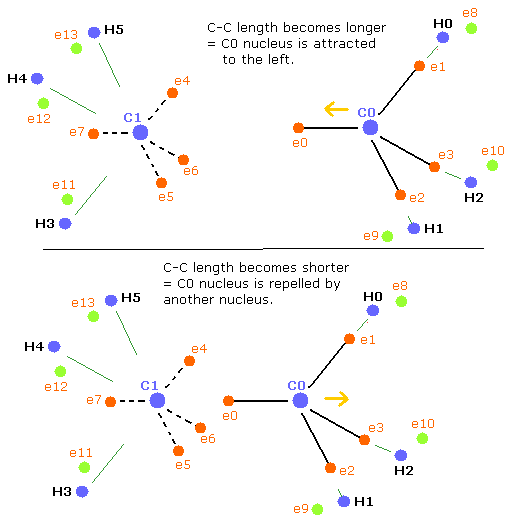
Basically when the repulsive forces of the four nuclei (three hydrogen nuclei + another carbon nucleus) are balanced, the carbon nucleus becomes stable.
But when the C-C length is longer than the balanced length, the influence of another carbon nucleus becomes weaker. (Fig. 5, upper panel)
As a result, the balance of the four repulsive forces breaks down, the "tetrahedral structure" is more broken to make the carbon nuclei stable (= FX, FY, FZ of C0,1 are small).
(In Table 3, the maximum error is 0.016, which is bigger than the control of Table 2.)
And the total potential energy (tV) is -806.74 eV, which is higher than the experimental value (-813.948 eV)
So the C-C bond in Table 3 is weaker than the control.
Fig. 5. balance of forces of ethane (H3C-CH3)
Next we choose the value 14000 in the scrollbar and click the C-C (MM) button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6190 | 0 | 0 | 6190 | 1592 | 0 | 0 | 0 | 1.996 |
| ele 1 | 2350 | 6070 | 0 | 6509 | 1192 | -9 | 3 | 0 | 2.003 |
| ele 4 | 2235 | 6100 | 0 | 6496 | 1993 | 42 | -8 | -43 | 2.007 |
| ele 5 | 2235 | -3050 | -5282 | 6496 | 1993 | 42 | -33 | 29 | 2.007 |
| ele 6 | 2235 | -3049 | 5282 | 6496 | 1993 | 42 | 42 | 14 | 2.007 |
| ele 7 | -6280 | 0 | 0 | 6280 | 2188 | 0 | 0 | 0 | 1.991 |
| ele 8 | 1800 | 1825 | -3705 | 4505 | 1011 | -246 | -609 | -2 | 1.002 |
| ele 10 | 1800 | 2296 | 3432 | 4505 | 1011 | -246 | 307 | -526 | 1.002 |
| ele 11 | 800 | 1945 | 3800 | 4343 | 1470 | -174 | -327 | 0 | 0.999 |
when the C-C length is shorter (=Table 4) than the balanced length, C0 nucleus is repelled by another nucleus, but on the other hand, C1 nucleus is closer to e0 electron.
So C1 nucleus is attracted to the right, and becomes unstable.(Fig. 5, lower panel)
As a result, the "tetrahedral structure" is more broken to make the carbon nuclei stable (= FX, FY, FZ of C0,1 are small).
(In Table 4, the maximum error is 0.009, which is bigger than the control of Table 2.)
Next we choose the value 13500 in the scrollbar and click the C-C (MM) button, which makes C-C length much shorter.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6180 | 0 | 0 | 6180 | 1354 | 0 | 0 | 0 | 1.987 |
| ele 1 | 2305 | 6095 | 0 | 6516 | 1190 | 2 | 0 | 0 | 2.007 |
| ele 4 | 2200 | 6200 | 0 | 6578 | 1934 | 55 | -10 | -46 | 2.024 |
| ele 5 | 2200 | -3100 | -5369 | 6578 | 1934 | 55 | -35 | 32 | 2.024 |
| ele 6 | 2200 | -3099 | 5369 | 6578 | 1934 | 55 | 45 | 14 | 2.024 |
| ele 7 | -6300 | 0 | 0 | 6300 | 2173 | 0 | 0 | 0 | 1.984 |
| ele 8 | 1800 | 1850 | -3680 | 4494 | 1011 | -247 | -623 | -1 | 1.000 |
| ele 10 | 1800 | 2261 | 3442 | 4494 | 1011 | -247 | 312 | -538 | 1.000 |
| ele 11 | 850 | 1980 | 3840 | 4403 | 1446 | -173 | -315 | 0 | 0.999 |
In Table 5, C0 nucleus is more repelled by another nucleus, and C1 is more attracted by e0 electrons. (Fig.5, lower)
So, to make the carbon nuclei stable (= FX, FY, FZ of C0,1 are small), "tetrahedral" structures need to be more broken than the upper case of Table 4.
In Table 5, the maximum error is 0.024, which is much bigger than the control of Table 2.
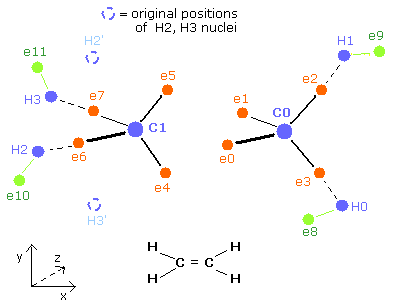
Here, the hydrogen electrons 11,12,13 are supposed to be closer to C nucleus than the hydrogen electrons 8,9,10. (Fig.3 upper).
(So the +X and +Y coordinates of ele 11 need to be positive.)
But if we try to make +X of ele 11 minus, the "nuc" value becomes shorter, which makes the "average" nuc much shorter than 4500 MM.
So we need to make +X and +Y of ele 11 positive.
Breaking all bonds ( 4 × C-H + C=C ) of ethylene (=ethene) requires 2253.1 kJ/mol (= 23.35 eV)
So the ground state energy of ethylene (8 carbon valence electrons + 4 hydrogen atoms) becomes -23.35 -148.024 × 2 -13.606 × 4 = -373.822 eV
According to the Virial theorem, the total potential energy (tV) becomes 2 × -373.822 = -747.644 eV.
The C=C and C-H bond lengths are 13390 MM, and 10870 MM, respectively. (1 MM = 10-14 meter).
And C=C-H angle is 121.3 degrees.
Fig. 6. Ethylene's electrons (H2C=CH2)
The ethylene molecule also consists of a pair of the 1st and 2nd versions of methane.
Between two carbon nuclei, the four electrons are attracted by another nucleus avoiding each other.
There is one problem in ethylene.
In case of ethylene, C=C-H angle of 121.3 degrees is bigger than ethane C-C-H angle of 111.17 degrees.
So we can not neglect the influence of the hydrogen electrons on the carbon nuclei.
The eight carbon valence electrons and two hydrogen nuclei are arranged "symmetrically" both in the 1st and 2nd versions of methane.
But the hydrogen electrons (e8-e11) are distributed "unsymmetrically".
(e10,11 of the 2nd version of methane is closer to the carbon nucleus than e8,9 of the 1st version methane like Fig.2.)
So the two carbon nuclei are attracted in the direction of the 2nd version of methane alternately.
As a result, the average forces of the hydrogen electrons acting on the carbon nuclei are zero.
Actually, in Fig.6, the orbits of e0,1 (1st version) is longer than e4,5 (2nd version) orbits like Fig.3. So the influences of hydrogen's electrons are balanced.
But here we use the Virial theorem. so we suppose that the long and short sides of elliptical orbits are the same, and we can not discriminate it.
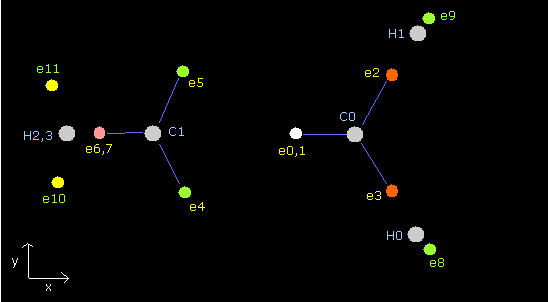
To average these forces of hydrogen electrons, we "temporarily" use 1st × 1st versions of methane as shown in Fig.6.
The total energy of each methane is the same, but we need to correct the interaction between hydrogen nuclei later.
(The original ethylene is a little bigger (0.681 eV) than Fig.6 in the total potential energy.)
Here we try to express the ethylene molecule using the next sample JAVA program.
About the detailed methods, see this page.
Sample JAVA program of ethylene (Virial theorem)
(If you copy and paste the program source code inside into a text editor, you can easily compile and run this.)
Fig. 7. Ethylene's electrons (H2C=CH2)
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -3869 | 0 | 5249 | 6520 | 2044 | -37 | 0 | -22 | 1.998 |
| ele 1 | -3869 | 0 | -5249 | 6520 | 2044 | -37 | 0 | 22 | 1.998 |
| ele 2 | 3500 | 5294 | 0 | 6346 | 1396 | 0 | 0 | 0 | 2.006 |
| ele 4 | 3750 | -5260 | 0 | 6459 | 2094 | 41 | 24 | 0 | 1.997 |
| ele 5 | 3750 | 5260 | 0 | 6459 | 2094 | 41 | -24 | 0 | 1.997 |
| ele 6 | -3568 | 0 | -5290 | 6380 | 1347 | 11 | 0 | -8 | 2.003 |
| ele 8 | 560 | -1100 | 4270 | 4444 | 1156 | -183 | 299 | 0 | 1.000 |
| ele 9 | 560 | 1100 | -4270 | 4444 | 1156 | -183 | -299 | 0 | 1.000 |
| ele 10 | -560 | -4280 | -1100 | 4454 | 1147 | 184 | 0 | 290 | 1.000 |
In Table 6, the total potential energy (tV) is -747.43 eV, which is almost same as the experimental value (-747.644 eV).
Next we choose "15000" in the scrollbar, and click "C=C (MM)" button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -3910 | 0 | 5260 | 6554 | 2033 | -16 | 0 | -10 | 2.003 |
| ele 1 | -3910 | 0 | -5260 | 6554 | 2033 | -16 | 0 | 10 | 2.003 |
| ele 2 | 3490 | 5210 | 0 | 6270 | 1490 | -6 | 4 | 0 | 1.994 |
| ele 4 | 3770 | -5270 | 0 | 6479 | 2095 | 22 | 14 | 0 | 2.003 |
| ele 5 | 3770 | 5270 | 0 | 6479 | 2095 | 22 | -14 | 0 | 2.003 |
| ele 6 | -3590 | 0 | -5197 | 6316 | 1431 | 21 | 0 | -16 | 1.990 |
| ele 8 | 600 | -1100 | 4290 | 4469 | 1152 | -189 | 301 | 0 | 1.001 |
| ele 9 | 600 | 1100 | -4290 | 4469 | 1152 | -189 | -301 | 0 | 1.001 |
| ele 10 | -610 | -4290 | -1100 | 4470 | 1146 | 193 | 0 | 293 | 0.999 |
When C=C length is longer (Table 7), the repulsive forces of the carbon nuclei becomes weaker, so the balance of the forces breaks down.
(It is similar to the ethane case of Fig. 5 upper panel.)
The "tetrahedral structure" is more broken to make the carbon nuclei stable (= FX, FY, FZ of C0,1 are small)
The maximum error is 0.010, which is bigger than the control of Table 6.
And in Table 7, the total potential energy is -717.74 eV, which is higher than the experimental value (= -747.644 eV).
So the binding force is weaker in Table 7.
Next we choose "12500" in the scrollbar, and click "C=C (MM)" button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -3850 | 0 | 5200 | 6470 | 2078 | -53 | 0 | -30 | 1.988 |
| ele 1 | -3850 | 0 | -5200 | 6470 | 2078 | -53 | 0 | 30 | 1.988 |
| ele 2 | 3500 | 5350 | 0 | 6393 | 1331 | 5 | -3 | 0 | 2.015 |
| ele 4 | 3750 | -5240 | 0 | 6443 | 2106 | 57 | 31 | 0 | 1.995 |
| ele 5 | 3750 | 5240 | 0 | 6443 | 2106 | 57 | -31 | 0 | 1.995 |
| ele 6 | -3620 | 0 | -5350 | 6459 | 1249 | 13 | 0 | -10 | 2.015 |
| ele 8 | 560 | -1150 | 4265 | 4452 | 1145 | -185 | 308 | 0 | 1.000 |
| ele 9 | 560 | 1150 | -4265 | 4452 | 1145 | -185 | -308 | 0 | 1.000 |
| ele 10 | -560 | -4280 | -1100 | 4454 | 1138 | 183 | 0 | 286 | 1.001 |
When C=C length is shorter (Table 8), the repulsive forces of the carbon nuclei becomes stronger.
(It is similar to the ethane case of Fig. 5 lower panel.)
The "tetrahedral structure" is more broken to make the carbon nuclei stable (= FX, FY, FZ of C0,1 are small)
The maximum error is 0.015, which is bigger than the control of Table 6.
These results show that the 13390 MM of C=C length is the balanced value.
About the acetylene (HC ≡ CH), see this page.
In the acetylene, the carbon electrons tend to be more attracted to another carbon nucleus, so "tetrahedral" structure of carbon is more broken than the ethane.
So the acetylene is more unstable and reactive.
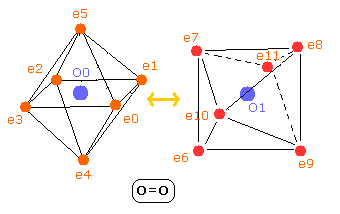
Breaking the O=O bond of the oxygen molecule requires 498 kJ/mol (= 5.16 eV)
So the ground state energy of oxygen molecule (12 oxygen valence electrons ) becomes -5.16 -433.103 × 2 = -871.366 eV
(433.103 eV is the sum of the 1-6th ionization energies of the oxygen atom.)
According to the Virial theorem, the total potential energy (tV) becomes 2 × -871.366 = -1742.732 eV.
And O=O length is 12074 MM.
Fig. 8. Oxygen molecule electrons (O=O)
Sample JAVA program of O2 (Virial theorem)
(If you copy and paste the program source code inside into a text editor, you can easily compile and run this.)
In this program, the central charge (+6e = +8e -2e) is supposed to be +6.271, so de Broglie's waves of single oxygen atom becomes just 2.000.
Fig. 9. Oxygen molecule electrons (O=O)
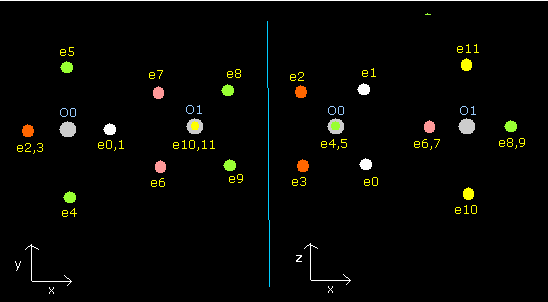
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3295 | 0 | -3165 | 4568 | 5832 | 0 | 0 | 0 | 1.985 |
| ele 1 | 3295 | 0 | 3165 | 4568 | 5832 | 0 | 0 | 0 | 1.985 |
| ele 2 | -3200 | 0 | 3260 | 4568 | 6004 | -4 | 0 | -4 | 2.002 |
| ele 4 | 10 | -4580 | 0 | 4580 | 5958 | -18 | 0 | 0 | 1.998 |
| ele 6 | -3295 | -3165 | 0 | 4568 | 5832 | 0 | 0 | 0 | 1.985 |
| ele 8 | 3200 | 3260 | 0 | 4568 | 6004 | 4 | -4 | 0 | 2.002 |
| ele 9 | 3200 | -3260 | 0 | 4568 | 6004 | 4 | 4 | 0 | 2.001 |
| ele 10 | -10 | 0 | -4580 | 4580 | 5958 | 18 | 0 | 0 | 1.998 |
| ele 11 | -10 | 0 | 4580 | 4580 | 5958 | 18 | 0 | 0 | 1.998 |
In Table 9, the total potential energy (tV) is -1741.3 eV, which is almost same as the experimental value (-1742.732 eV).
The oxygen nuclear charge is bigger than carbon, so the de Broglie's waves is a little more unstable than the carbon case.
Next we choose "13000" in the scrollbar, and click "O=O (MM)" button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3295 | 0 | -3178 | 4577 | 5848 | -6 | 0 | -6 | 1.988 |
| ele 1 | 3295 | 0 | 3178 | 4577 | 5848 | -6 | 0 | 6 | 1.988 |
| ele 2 | -3200 | 0 | 3263 | 4570 | 5997 | -5 | 0 | -5 | 2.001 |
| ele 4 | 5 | -4584 | 0 | 4584 | 5943 | -13 | 0 | 0 | 1.998 |
| ele 6 | -3295 | -3178 | 0 | 4577 | 5848 | 6 | -6 | 0 | 1.988 |
| ele 8 | 3200 | 3263 | 0 | 4570 | 5997 | 5 | -5 | 0 | 2.001 |
| ele 9 | 3200 | -3263 | 0 | 4570 | 5997 | 5 | 5 | 0 | 2.001 |
| ele 10 | -5 | 0 | -4584 | 4584 | 5943 | 13 | 0 | 0 | 1.998 |
| ele 11 | -5 | 0 | 4584 | 4584 | 5943 | 13 | 0 | 0 | 1.998 |
When O=O length is longer (Table 10), the repulsive forces of the oxygen nuclei becomes weaker
But in Table 10, the total potential energy is -1738.93 eV, which is higher than the experimental value (= -1742.732 eV ).
So the binding force is weaker in Table 10.
Next we choose "11000" in the scrollbar, and click "O=O (MM)" button.
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3295 | 0 | -3154 | 4561 | 5777 | 20 | 0 | 19 | 1.981 |
| ele 1 | 3295 | 0 | 3154 | 4561 | 5777 | 20 | 0 | -19 | 1.981 |
| ele 2 | -3195 | 0 | 3269 | 4571 | 5999 | -7 | 0 | -7 | 2.004 |
| ele 4 | 15 | -4582 | 0 | 4582 | 5960 | -27 | 0 | 0 | 1.998 |
| ele 6 | -3295 | -3154 | 0 | 4561 | 5777 | -20 | 19 | 0 | 1.981 |
| ele 8 | 3195 | 3269 | 0 | 4571 | 5999 | 7 | -7 | 0 | 2.004 |
| ele 9 | 3195 | -3269 | 0 | 4571 | 5999 | 7 | 7 | 0 | 2.004 |
| ele 10 | -15 | 0 | -4582 | 4582 | 5960 | 27 | 0 | 0 | 1.998 |
| ele 11 | -15 | 0 | 4582 | 4582 | 5960 | 27 | 0 | 0 | 1.998 |
When O=O length is shorter (Table 11), the repulsive forces of the oxygen nuclei becomes stronger.
So the "octahedral structure" of oxygen is more broken to make the oxygen nuclei stable (= FX, FY, FZ of O0,1 are small)
The maximum error is 0.019, which is bigger than the control of Table 9.
The oxygen molecule is more unstable and reactive than H2O.
It is thought that this property of O2 can be explained by the unstable wave's values of Table 9.

2010/12/6 updated. Feel free to link to this site.