Top page (correct Bohr model including the two-electron atoms)
Strange "spin" is NOT a real thing
History of old Bohr's helium and classical atoms.
If you try to cure some fatal illnesses such as cancers, what you first think of are some nanomachines or nano-moleuclar devices to distinguish cancerous cells from normal cells.
To do such treatments correctly, we need to know and handle the interactions among atomic (+molecular) electrons and nuclei completely.
Of course, in any other fields such as physics and chemistry, "nanotechnology" is a very important thing.
But when you start to study quantum mechanics and chemistry, you will find that the present quantum chemistry is very far away from what you have expected.
These "mathematical" quantum chemistry, which has very vague and inefficient nature, is one of the main reasons why I start to doubt the quantum mechanics.
So I would like you all to know about the present state of this weird quantum chemistry.
( Unfortunately, in the ordinary textbooks, we see ONLY "hydrogen" atoms, and can hardly find multi-electron atoms such as heliums. Why ?? )
(Fig.1) "Mathematical" Schrodinger equation vs. "real" Bohr model.

As you know, we can not know what the Schrodinger wavefunctions really mean.
And we can not know what the electron's spin and Pauli exclusion principle really are.
So all we can do is to believe and solve Schrodinger equation even in complicated multi-electron atoms and molecules.
( Of course, the equations in the multi-electron atoms can not be solved, so we have to use some approximations. )
This means we can NOT try more useful and flexible methods in the interactions among various atoms, as long as we are restricted within the quantum mechanics.
(Fig.2) Quantum mechanical helium is unstable ?
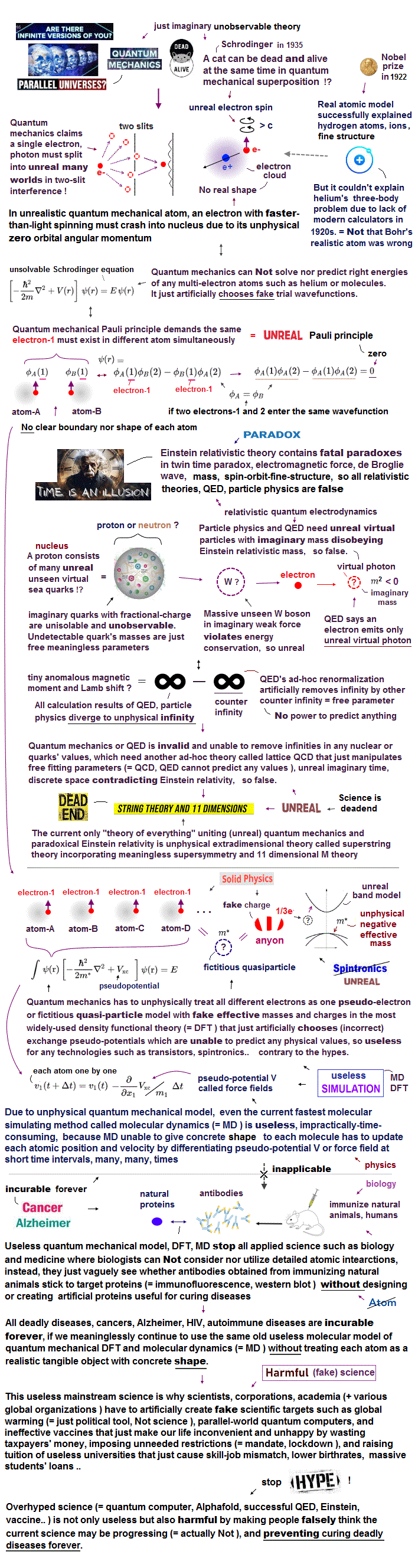
According to the quantum mechanics, the angular momentums of both two electrons in helium are zero ( L = 0 ).
This means the two electrons often collide with helium nucleus and rebound from it ?? (Fig.2A)
Do you think this quantum mechanical helium can be stable ? ( I don't think so. )
By the way, what is the helium's configuration in the quantum mechanics ?
We often see the hydrogen's configuration in the textbooks, but can NOT find the helium atom at all. Why ?
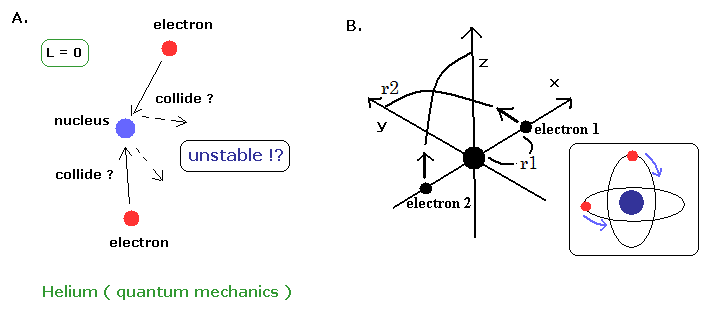
(Eq.1)
When Z=2, Eq.1 means the Hamiltonian of the helium atom. ( Δ = ∇2 )
When we try to get the correct value of the ground state energy of the helium atom, we have to use more than a thousand- terms variational functions of
(Eq.2)
Of course, we can NOT imagine the helium's actual configuration from these many mathematical terms of Eq.2.
And this calculation value is -79.015 eV, which is a little different from the experimental value of -79.0051 eV.
On the other hand, our new Bohr's helium atom in the top page can get more correct answer of -79.0035 eV.
( This little difference between 79.0035 eV and 79.0051 eV is what we call "relativistic" effect, which value is good. See also this page. )
The important point is that in our Bohr's method we get the clear atomic view and electron's orbital radius in the two important inner 1s electrons. (See also this page.)
So we can make use of these Bohr models in other atoms or molecules easily and correctly.
On the other hand, the long list of mathematical terms of Eq.2 is completely useless.
We can NOT apply these many meaningless terms of helium to other atoms or molecules.
This means the present quantum mechanical methods are useless as "nanodevices".
(Fig.3) The relation between Quantum mechanics and Relativity.

In 1920s, Bohr model could not show correct helium atomic model.
Because the helium atom (or any other atomes or molecules ) is the three-body problems, which needs computers to solve it.
On the other hand, the quantum mechanical variational methods could get the approximate value of helium ground state energy.
( But as I said above, these quantum mechanical methods can NOT show the concrete model. )
If the helium atom (= two electron inner shell structure ) had not beed defined, the developments of all physics and chemistry would have stopped.
So all we could do was to accept the weird quantum mechanics and quantum chemistry.
From 1920s to 1980s - 1990s, when the computers become popular, the fine structure of Bohr-Sommerfeld model was replaced by relativistic Dirac equation.
And based on this very influential Dirac equation (+ Maxwell eqiation ), QED (1930s ) and standard model (1960s) were created.
Of course, as Dirac equation relies on special relativity, all these theories depend on special relativity.
And the final state of these theories is a strange 10-dimensional string theory.
So if we try to go back to Bohr-Sommerfeld model, all these theories need to be revised.
And as long as we don't admit some "ether" in the vacuum, we have to rely on the "unreal" virtual particles forever.
Frankly speaking, all these very influential fundamental theories such as the quantum field theory and relativity obstruct the development of "real" science, I think.
( From the top page, you can see total revisions of these theories. )
The important point is that ordinary people do NOT know the present states of these complicated "mathematical" physics well.
This is a serious problem.
( About the complicated quantum field theory and QED, even physicists (of course chemists ) in other fields do not know well.)
The images of them as shown in TV or various popular books are NOT the truth.
Present quantum chemistry such as density functional theories (DFT) and molecular ortbital methods are based on Hartree-Fock methods.
Of course, all these methods are based on Schrodinger equation and Pauli exclusion principle.
In these theories, Hamiltonian (= H ) including n electrons is
(Eq.3)
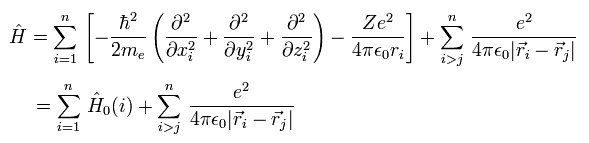
where the first term ( of the first line ) means the electrons' kinetic energies.
The second term is the Coulomb energy between each electron (= -e ) and nucleus (= Ze ).
And the third term is the Coulomb repulsive energy between electrons.
Here we use the notation of
(Eq.4)
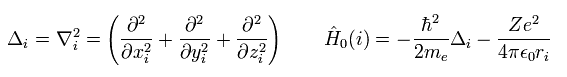
As you know, the Schrodinger equation can NOT be solved except in one-electron hydrogen atom.
So we have to use some approximation.
In multi-electron atoms, we usually use one-electron approximation, where we define the wavefunction as
(Eq.5)
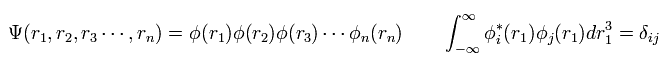
where each wavefunction is supposed to satisfy orthonormal system.
( Because, this system is easy to calculate. )
Of course, the form of the wavefunctions of Eq.5 is NOT true.
Considerting the complicated interaction terms among electrons (= third term of Eq.3 ), the total wavefunction of Eq.5 becomes more complicated.
( Of course, we have to consider Pauli exclusion principle, too. )
Like Eq.5, when the wave function of each electron can be separated, this is called "one-electron approximation".
The expectation value (= E ) of Hamiltonian Eq.3 is
(Eq.6)

Using Eq.5 and the orthonomal property, we get the total energy expectation value of
(Eq. 7)
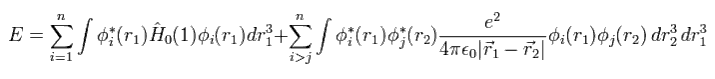
So, to know the correct values, we have to solve all Schrodinger equations of
(Eq. 8)
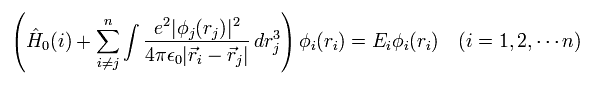
But to slove Eq.8, we need to know the first state of each wavefunction (= φi ) from the beginning, because Eq.8 uses these φ as interaction operators among electrons.
So we choose some trial (test) functions as φi, and solve Eq.8.
( Of course, this calculation is very difficult. )
And when we get the results of the new wavefunction φ, we use these new wavefunctions in Eq.8, and calculate it again.
Untill we get the correct wavefunctions, we need to continue these very complicated and hard calculations.
This is called self-consistent field (SCF) methods.
This SCF methods are used also in density functional theory (DFT).
Do you want to apply these very complicated quantum mechanical methods to various fields such as molecular biology and nanotechnology ?
Of course, Eq.5 is NOT complete.
According to Pauli exclusion principle, each state can not include more than two electrons.
For example, in the lithium atom, the ionization energy of the third electron is much smaller than other two inner electrons.
So considerring the two spin states (= α and β ),
(Eq.9)
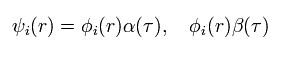
Total wavefunction of Eq.5 becomes
(Eq.10)
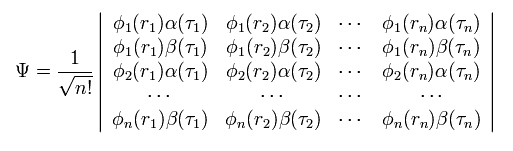
where the total wavefunction Ψ is a determinant.
As you know, in the determinant, when any two lines (or rows) of the matrix are the same, this determinant becomes zero.
They use this property of the determinant as Pauli exclusion principle.
But due to this very complicated determinant, we can NOT apply the present quantum chemistry to various other fields easily.
This means that we ourselves prevent our development of the science within the quantum mechanics.
For example, in the case of the two electrons, the determinant becomes
(Eq.11)
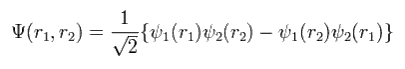
where
(Eq.12)
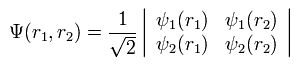
If ψ1 = ψ2, Eq.11 becomes zero.
And when we interchange r1 and r2 in Eq.11, the sign of the total wavefunction Eq.11 becomes opposite.
So they insist the determinant shows the antisymmetric property of the fermions such as electrons.
But as shown in this page, antisymmetric property originates in the relativistic Dirac equation ( NOT related to Schrodinger equation ).
And this anticommutation relation of fermions contradicts original de Broglie theory.
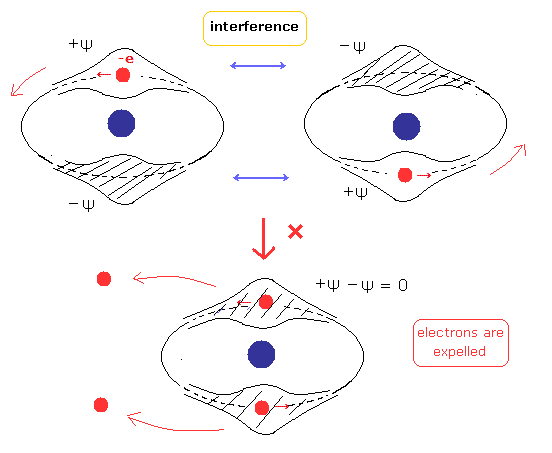
Instead of depending on these very vague nature, if we use the clear interpretation about Pauli exclusion principle based on the de Broglie wave interference, the calculation becomes much easier.
( See Why there aren't any compounds in Helium atom and strange spin. )
(Fig.4) Two de Broglie waves of electrons interfere with each other.
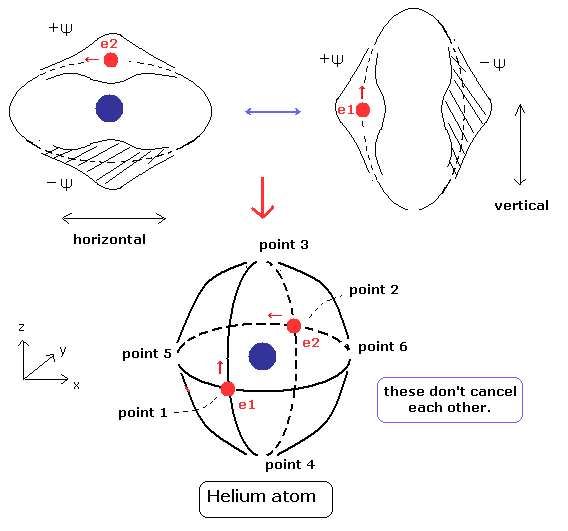
(Fig.5) Stable and independent two de Broglie waves. (= perpendicular to each other.)
Using Eq.10, the expectation value becomes
(Eq.13)

where J terms mean the ordinary Coulomb repulsive energy between electrons.
And K terms are exchange integral, which express Pauli exclusion principle.
The important point is that this exchange integral K includes ONLY the same spin states ( αα or ββ )
The different spin states (= αβ ) become zero by the orthogonality of α and β.
For example, in the helium atom, only H0 and J terms of Eq.13 are left.
( This case is allowed, because the states of the two electrons are the same. )
But in the multi-electron atoms, there are different states with different spin states.
Eq.18 can not explain these multi-electron states correctly, though it is very complicated.
Full configuration interaction ( full CI ) and ab initio methods belong to this category.
But basically, it is impossible to get the correct values, because basal functions ( basis set) available are limited.
So we must consider other simpler and more efficient theories as early as possible.
Now, Density functional theory (DFT) dominates the present quantum chemical world due to its easier calculation methods.
But density functional theory is one of approximations.
And after all, DFT needs to solve Schrodinger equation and use self-consistent field methods.
So basically the situation has not changed even in DFT.
See also ab-initio DFT is NOT ab-initio.
In this section, we write the distance between the two particles like
(Eq.14)
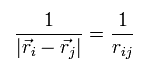
Each wavefunction is supposed to form an orthonormal set like
(Eq.15)

where Ψ means a determinant, as shown above.
Total electron density ρ(r) is expressed as
(Eq.16)
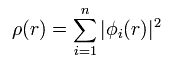
This means density ρ(r) is a square value of wavefunction φ.
Like Eq.13, using density ρ(r), the expectation value of Hamiltonian becomes
(Eq.17)
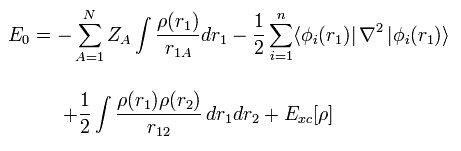
where the coefficient 1/4πε and h, m are omitted.
Here N positive (+Ze) nuclei are supposed to exist.
The first term of Eq.17 means the Coulomb attractive energy among nuclei and electrons.
And the second term of Eq.17 means the kinetic energy.
The third term of Eq.17 mean the Coulomb repulsive energy ( like J of Eq.13 ).
The last term of Exc mean exchange-correlation energy which includes K and any other interactions.
Considerring density ρ is a square of each wavefunction (Eq.16), the functional derivative of the expectation value E with respect to ρ becomes
(Eq.18)
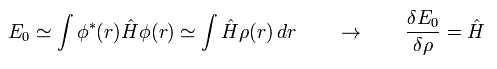
Functional derivative acts on the functions inside the integral.
In the same say, the functional derivative of the kinetic energy (= second term of Eq.17 ) becomes
(Eq.19)
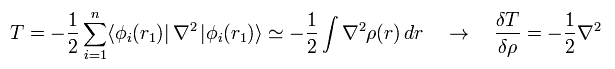
The functional derivative of the Coulomb interaction term (= first term of Eq.17 ) between nuclei and electrons is
(Eq.20)
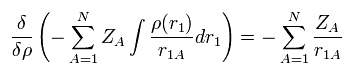
The functional derivative of the Coulomb repulsive term (= third term of Eq.17 ) between electrons is
(Eq.21)
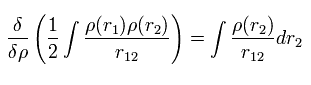
From Eq.17, Eq.18, Eq.19, Eq.20 and Eq.21, the Hamiltonian and its eigenfunction become
(Eq.22)
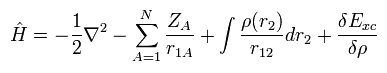
(Eq.23)
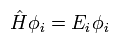
So after all, we have to solve very complicated Schrodinger equation of Eq.22 and Eq.23 even in DFT.
Of course, the most difficult term of exchange-correlation energy Exc is unknown.
One of approximations is local density approximation (LDA).
In the LDA, the positive and negative charge densities are supposed to be uniform and equal to each other (= neutral ).
So under this very special case, Hamiltonian leaves only kinetic energy, like
(Eq.24)
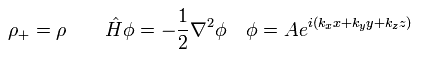
The exchange-correlation energy Exc can be separated like
(Eq.25)
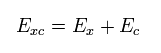
where
(Eq.26)
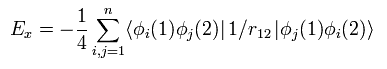
Eq.26 means the exchange energy like K of Eq.13.
Only the same spin states are left, as explained above.
So in the closed shell, 1/4 is added.
Substituting the free particle state of Eq.24 into Eq.26 and solving it, we get the approximate value of
(Eq.27)
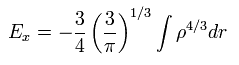
And furthermore we have to solve Schrodinger equation of the uniform density to get E0.
Based on these calculation resutls, we can know the remaining Ec from
(Eq.28)
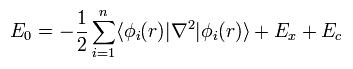
First, we need to choose some approximate function of
(Eq.29)
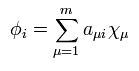
Using Eq.27 and Eq.29, we solve Eq.22 and Eq.23 to get the new wavefunctions.
Using these new wavefunctions, we repeat the calculation of Eq.22 and Eq.23 .....
( = Self-consistent field theory )
So the complicated situation has NOT changed even in DFT.
( Furthermore, DFT is only an approximation, which can not get the real value. )
Instead of depending on these old quantum mechanical methods, we should use the new Bohr's methods as shown in top page to make the calculation more efficient.
In new Bohr model, all we have to consider is Coulomb forces and an integer times de Broglie wavelength (+ their interference ).
The good things of Bohr model is that we can think about and try various concrete and easier ways, because we grasp the clear configuration of the atoms and molecules.
On the other hand, the methods based on Schrodinger equation + Pauli exclusion princile, we can NOT get away from their very strict restriction, because we do NOT know what they really mean.
So all we can do is to believe in "mathematical" Schrodinger equation and strange spin.
( See also Schrodinger equation is a wrong version of Bohr-Sommerfeld model ?.)
(Fig.6) "Cooper pair" really exists ??
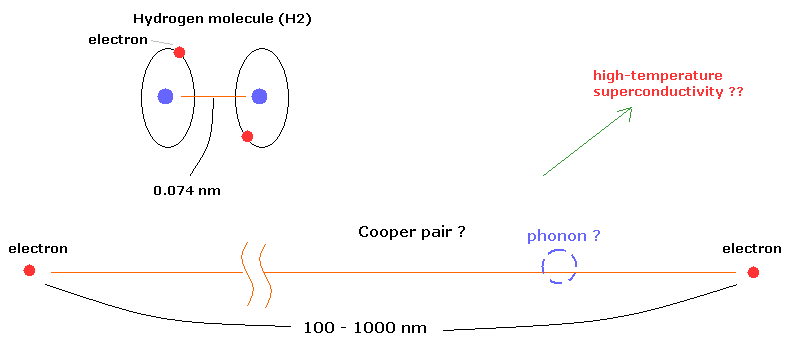
According to the present condensed matter physics, it is said that a Cooper pair is two electrons that are bound together at low temperature through the vague existences of "phonons".
Surprisingly, the distance between the two electrons in the Cooper pairs is about 100- 1000 nanometer (nm) !
For example, in the hydrogen molecule (H2), the distance between two nuclei is about 0.073 nm.
How can these two electrons bind stably to each other in the superconductor ? This is strange.
According to the standard interpretation, positive ions (nuclei) are said to be related to this very long binding as a quasiparticles such as phonons.
( But I think, this very long binding is very unnatural. How do you think about it ? )
According to BCS theory, under some low temperature, the Cooper pair is formed in the superconductivity.
So the present BCS theory can not explain high-temperature superconductivity.
As shown in this page (Eq.15 - Eq.18), if we use the usual Bohr model and an integer times de Broglie wavelength, we can explain quantized magnetic flux without strange Cooper pair.
Of course, if Cooper pair doesn't exist, the problem in the high-temperature superconductivity does NOT occur.
Probably the concept of Cooper pair was introduced to explain boson-like nature (= fermion + fermion) and quantized magnetic flux in the superconductor.
But do you think strange electron spin does not exist from the beginning ? ( See this page. )
When we apply some external magnetic fields and cool the material to the superconductor, the magnetic field inside the superconductor becomes zero.
According to the standard interpretation based on the present condensed matter physics, this zero magnetism is caused by the mechanism in which the photon with zero mass gains "mass".
Because the force caused by the photon with mass does not reach far away.
( According to the relativity, Coulomb force is said to be caused by the strange "virtual photons" not by ether. )
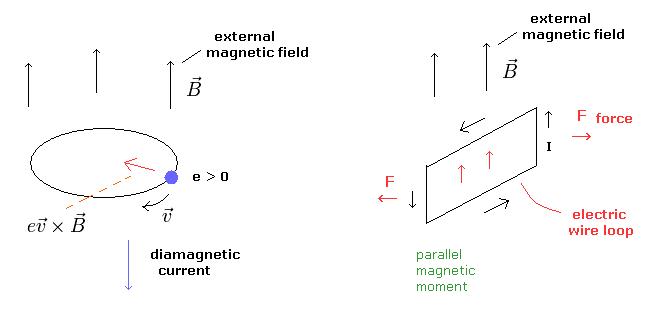
But I think this mechanism can be explained only by classical electromagnetism (= Maxwell theory ), in which Lorentz force causes diamagnetism ( Fig.7 left panel ).
When the motion of each charged particle is still more influential than the overall de Broglie wave not in the superconductor, the magnetic moments of these circular motions tend to be parallel to the external magnetic fields ( Fig.7 right panel ).
According to the present quantum mechanics, the charged particle must have "spin".
So we need to erase these strange "spin" to explain the diamagnetism, which causes very long binding pair mentioned above, I think.
Because the magnetic moments of these spin tend to be parallel to the external magnetic field.
By the way, what is the "concrete" state of photon with "mass" ?
(Fig.7) Diamagnetism and ferromagnetism.
Even in the nonrelativistic quantum field theory such as condensed matter physics, the very vague concepts such as creation, annihilation operators and spontaneous symmetry breaking.
But the reason why the present quantum field theory becomes a very abstract thing is due to very strict restriction by the relativity.
So in the nonrelativistic physics, we need not use this vague quantum field theory, I think.
For example, the interaction between electrons and phonons can be expressed as
(Eq.30)

And in the symmetry breaking, we use the "mathematical" expression like
(Eq.31)
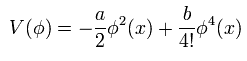
But do you think we can naturally explain these spontaneous symmetry breaking under very low temperature from the viewpoints of the ordinary classical mechanics ?
At very low temperatures, each particles' independent motions become very inactive.
So it is natural that the overall de Broglie's wave effect becomes stronger at very low temperatures.
So we can explain various phenomena such as ferromagnetism and superconductor by the usuall classical mechanics (+ de Broglie theory.), I think.
And Dirac particle with zero mass contradicts the original theory even though it is a quasiparticle ?
We should reconsider the real natures of quasiparticles such as spinons ( carrying spin ? ), orbitons ( carrying orbital location ? ), and holon ( carrying the charge ? ), I think.

2012/7/26 updated. Feel free to link to this site.