Top page (correct Bohr model )
Strange "spin" is NOT a real thing
Singlet Triplet don't mean "spin".
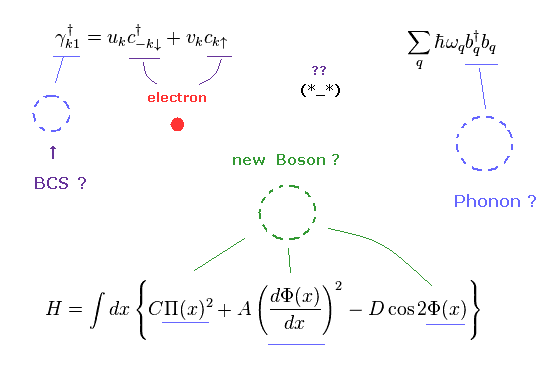
(Fig.1) Many unreal quasiparticles ! = Condensed-matter physics.

Most textbooks say the quantum mechanics is most successful theory, which can explain various latest technology.
But in fact, now in this 21th century, this ancient quantum mechanics clearly obstructs the development of science.
Researchers in these fields just aim at illusory particles, and wasting extremely much time.
As shown in Fig.1, the current condensed matter physics depends on many imaginary quasiparticles.
Researchers try to create convenient quasiparticles to fit some "math" models to experimental results.
These are just tricks, NOT real objects at all, as I say in this page.
To be precise, Bogoliubov particle (= γ ) in BCS theory is one of quasiparticle fermions.
And "phonon" is quasipaticle "boson". Of course, both are unreal.
Surprisingly, many unreal particles appear in this quantum mechanics. ( See Wiki. ) Very disastrous fact.
(Fig.2) "Spin" and "Charge" are separated ??
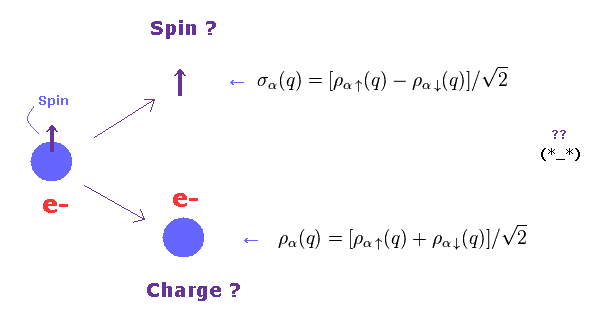
In this unreal solid state physics, "Spin" and "Charge" of one particle can be separated, they insist.
These are called "spinon" and "holon".
Of course, as shown on this site, these quasiparticles don't really exist.
But they try NOT to clarify what these unreal quasiparticles really are (= Shut up and calculate ! ).
As a result, only very abstract math symbols like Fig.2 are left in the latest quantum mechanics.
Furthermore, this site says they succeeded in separating electron into three components such as "Spin", "Charge" and "Orbiton" (= orbital motion ).
So the present condensed matter physics is very far from real physics, and just aiming at fantasy.
(Fig.3) Fermions without "Spin" !?
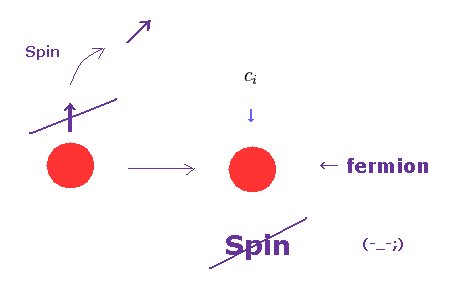
Surprisingly, the present condensed matter physics utilizes spinless fermions. ( See this site p.19 or this site . )
As you know, fermion always has spin 1/2.
There are NO spinless fermions in the current quantum mechanics.
So these theories are clearly self-contradictory.
Of course, as I explain in this page, these spinless fermions are just math ( NOT physics ) symbols, have NO reality.
The problem is that they try NOT to investigate what these spinless fermions really are (= Shut up and calculate !, again. )
So under the existing circumstances, the science stops at these unreal quasiparticles.
(Fig.4) Interaction between Phonon and electron !?
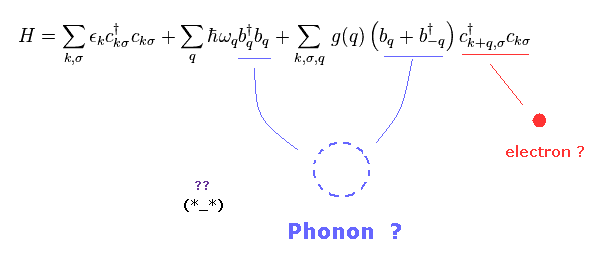
The present superconductivity including high temperature is basically based on quasiparticle phonons and Cooper pair.
But as you see Fig.4, these phonons and their interactions are just abstract math operators.
There are NO concrete physical images at all.
As you know, actual particles in this world are NOT math operators.
(Fig.5) Phonon mechanism can be replaced by an integer multiple of de Broglie wavelength.
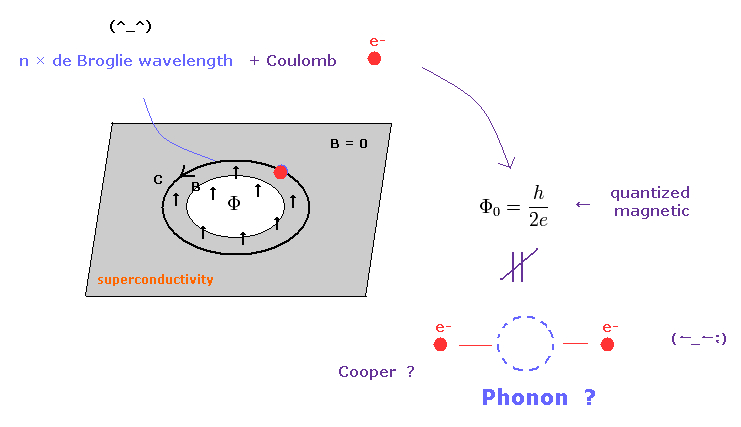
The reason why they believe phonons and Cooper pair is quantized magnetic flux (= Φ = h/2e ).
( As far as I check, this is the only direct experimental result of this Cooper pair. )
As shown on this page, this phonon based Cooper pair uses vector potential A.
In fact, this Cooper pair phonon also relies on an integer multiple of de Broglie wave as "phase" .
( They should make clear what this "phase" really is, as soon as possible. )
On this page, we can prove this quantized magnetic flux means real de Broglie wave and classical Coulomb force.
The important difference between this de Broglie theory and phonon mechanism is "reality".
We don't need phonons in this flux quantum, because they are unreal.
(Fig.6) "Imaginary" time is real ??
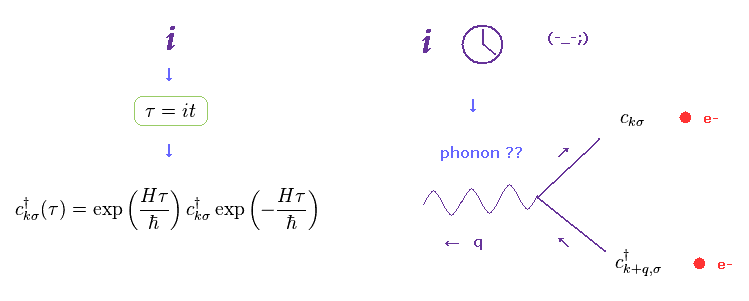
In fact, all mechanisms involved in "phonon" rely on unrealistic imaginary time ( t = -iτ ).
Propagator (= Green's function ) is often used to calculate the change of the states with time.
Of course, all physical phenomena in this real world change with real ( NOT imaginary ) time.
So the current condensed matter physics is completely out of touch with reality.
(Fig.7) "Imaginary" time is necessary for incorporating Boltzmann factor.
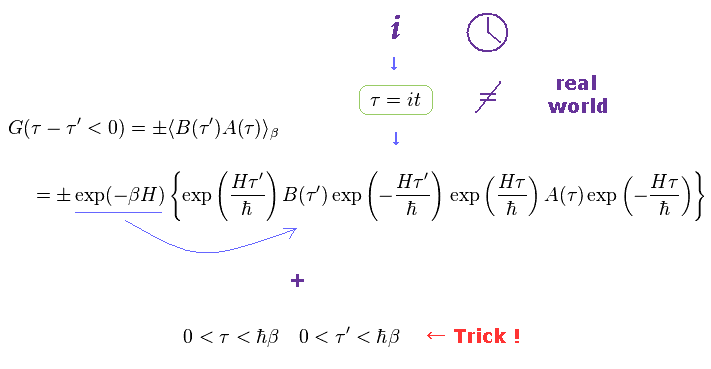
At finite temperature, Boltzmann factor gives probability of some states with respect to their energy (= H ).
They try to incorporate this Boltzmann factor (= blue line ) into propagator, so they transform real time into imaginary !
This artificial method is for getting some discrete frequencies ( of course, "imaginary" frequency ).
These discrete frequencies based on Boltzmann factor are completely different from continuous frequencies of real time.
As you know, all phenomena in this real world are changing with real time.
So the calculated results based on this imaginary time are just fictions.
QCD also depends on imaginary time, so both these theories lack reality.
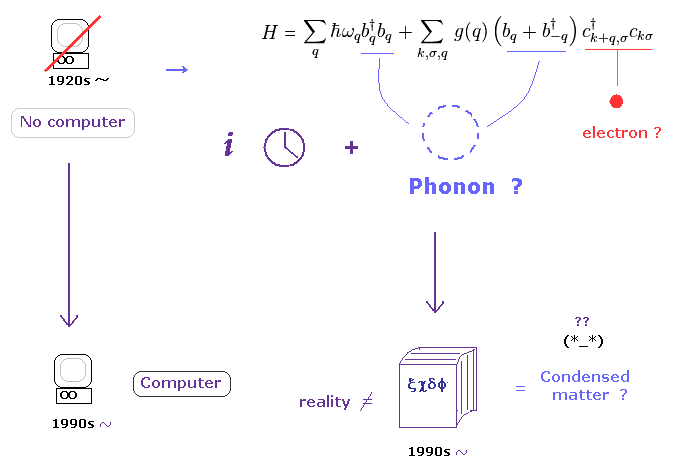
(Fig.8) Time gap without computers made condensed matter physics "unrealistic" math.
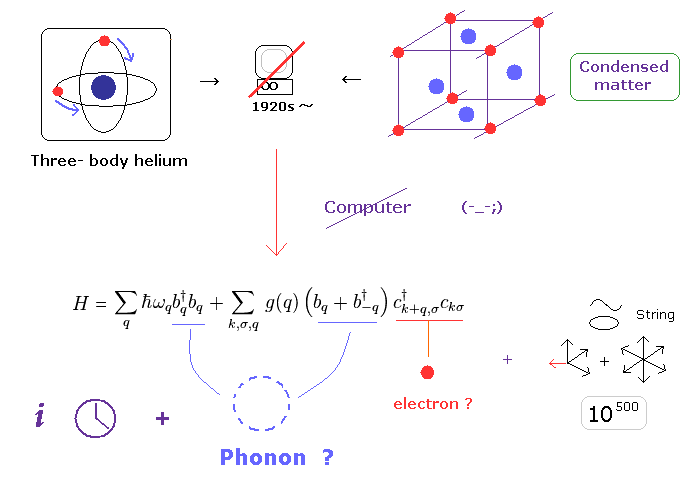
In 1920s when quantum mechanics was born, there were NO computers.
So the researchers at that time were NOT able to compute three-body helium atom using computers.
Of course, if three body helium couldn't be treated, it is much more impossible to compute more complicated condensed matter, which contains almost infinite atoms
But even in these serious situations, researchers had to continue researching and publishing papers for better posts.
So many kinds of unrealistic quasiparticles were artificially created as mathematical tools.
In high energy physics, unrealistic 10-dimensional string theory is left as the only unified theory. This is disaster.
As you notice, these fictitious theories were needed to fill time gaps from 1920 to 1990s -.
(Fig.9) Condensed matter physics = Ancient documents filled with math "hieroglyph".
In about 1980, the Apple II was produced as the first all-in-one computer.
But we needed to wait for more powerful computers until 1990s to deal with complicated molecular interactions.
As I said, this extremely long ( 1920 - 1990 ) time gap caused many unrealistic theories.
Even after highly efficient computers appeared in 1990s, the conventional math ( NOT physical ) quasiparticles and old methods were left like ancient spells.
At first glance, you will find these old approaches become ancient documents, and NOT effective at all now in 21th century.
Because quasi- and virtual particles themselves are unreal.
(Fig.10) How "fantasy" theories were made ?
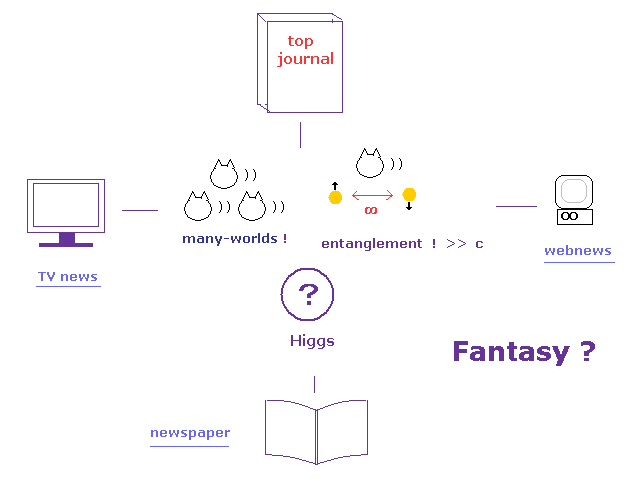
Quantum mechanics has NO reality.
But there were no other theories left under the conditions of NO computers in 1920s.
So even various ( top ) journals deal with these fictitious phenomena now in 21th century.
These theories are completely unrealistic, so they made NO progress at all ( ex. quantum computer ).
The serious problem is various mass media such as TV news, webnews, and newspapers are promoting these fantasy theories.
They are deceiving ordinary people, and giving bad influences to them.
They must make efforts to report experimental results as they are, NOT hiding their defects. ( This is the true role of mass media, I think. )
For example, Higgs news got quickly around the world last year.
But in spite of these vast news, ordinary people don't understand clear mechanism how Higgs gives mass to elementary particles.
Mass media try to report ONLY attractive parts, and
(Fig.11) They can deal with Only "Ratio" of Macro effects, NOT absolute values.
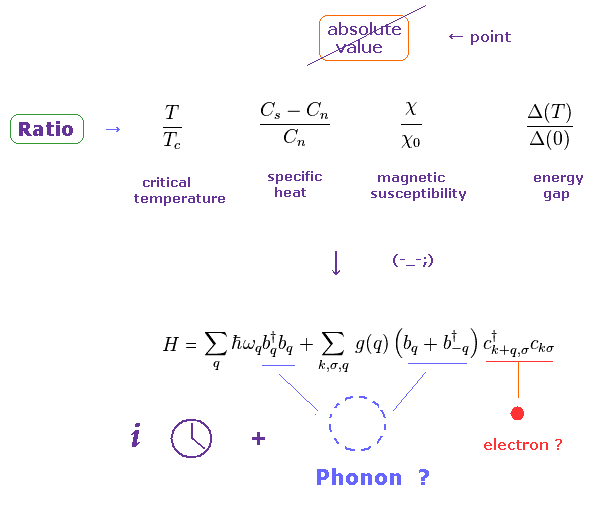
Due to unrealistic spin and wavefunction, the current condensed matter physics cannot get into
All they can deal with are ONLY macro effects such as critical temperature, specific heat, magnetic susceptibility, and energy gap.
Furthermore, the present spin models are too abstract, so it is impossible to predict absolute values of them.
They just try to utilize many kinds of artificial quasiparticles and imaginary time to fit them with experimental results of "Ratio" ( NOT absolute values ! ).
As far as we are bound with incorrect models, we cannot get into microworlds of actual particles' interactions.
(Fig.12) Neutron scattering = spin wave or Phonon ??
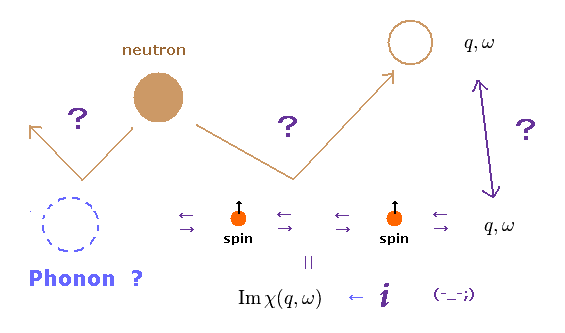
The direct experimental facts of unreal phenomena such as Phonons and Spin wave are ONLY neutron ( or light ) scattering.
They don't see these phonons and spin waves directly.
They just estimate their existences ONLY from the energy change of scattered neutrons.
( ex. Energy transition: neutron → phonon, phonon → neutron ).
Though phonons are just quasiparticles, which don't really exist.
(Fig.13) There are No choices other than "Phonons" as atomic vibrations.
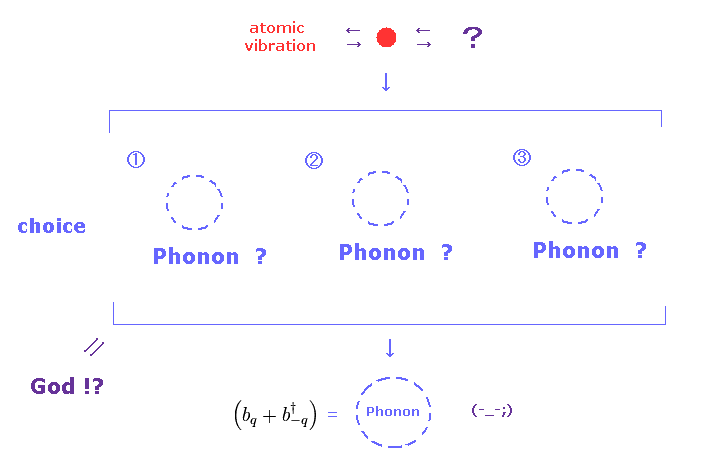
Neutrons are scattered mainly from nuclei and magnetic moments.
Nuclear scattering is very complicated, because neutron is scattered by nuclear internal force.
So neutron scattering can be some sensor of nuclear (= atomic ) vibration.
But the present mathematical quantum mechanics cannot treat many-body effects, even if we use computers.
( Because, quantum mechanics was originally the theory, which is independent from computers. )
All they can depend on is very abstract math operator.
This is the main reason why they try to rely on unreal quasiparticles (= Phonons ) as atomic vibrations.
(Fig.14) There are No choices other than "Spin" as magnetic moment.
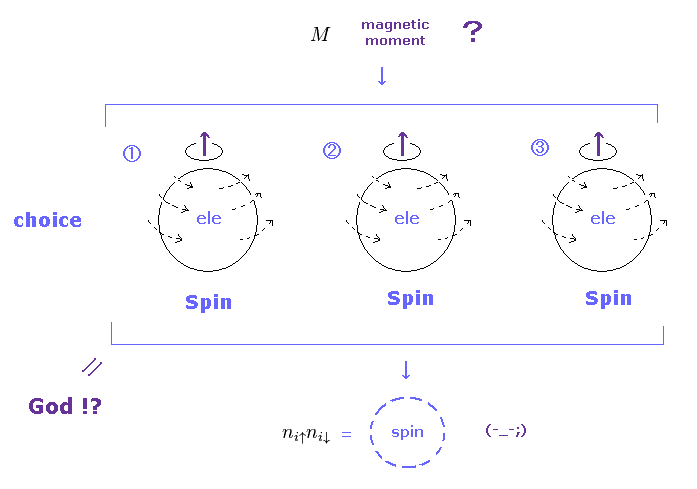
One of the two main scattering factors is magnetic moment.
Magnetic moment is very weak, but electron's orbital is spreading much wider than nuclei, so this effect is as big as nuclear scattering.
The important point is that the present condensed matter physics consider ONLY "Spin" as the origin of magnetic moments.
So if they observe some fluctuations of magnetic moments, they easily jump to the conclusion that these fluctuations are from "Spin".
They neglect any other large magnetic moment fluctuations such as orbital motions.
As shown on this page, these spin fluctuation theories are filled with mathematical tricks, and lack clear images.
(Fig.15) Two fermions is equal to Four fermions ? Why ? Trick ?
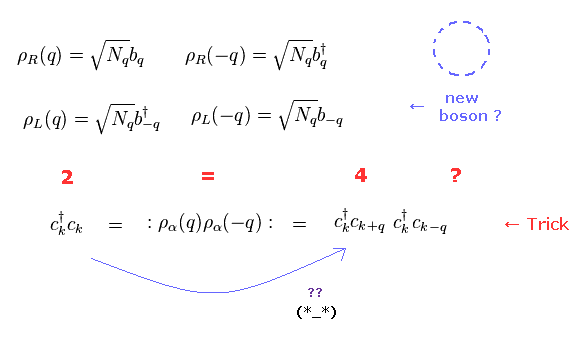
For spin Peierls and separation of spinon and holon, we need to use artificial mathematical tricks such as Fig.15.
Surprisingly, in Fig.15, they consider two fermions (= c†c ) is equal to four fermions (= c†cc†c ).
So the equation of " 2 = 4 " holds, they insist.
Why does this strange situation occur ? ( See also this site . )
And you need to remember there are NO physical images from here.
Even the latest condensed matter physics is just math symbols, NOT physics.
(Eq.1)
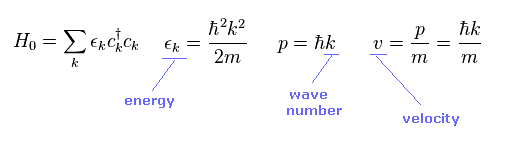
In Eq.1, c† and c mean creation and annihilation opearators of electrons.
"k" and "p" mean wavenumber and momentum. ( Here ħ is omitted, so, k = p. )
ε means energy.
(Eq.2)
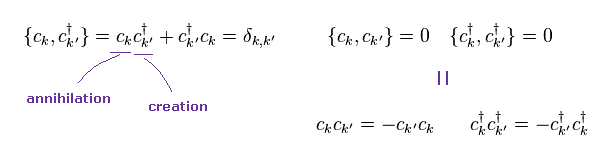
These electron's operators satisfy anticommutation relation of Eq.2.
This relation is the origin of Pauli exclusion principle, they insist.
But as you see, these are just math rule without physical entity.
(Eq.3)
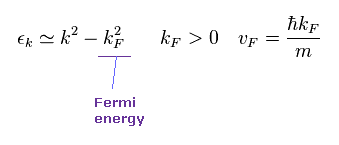
kF and vF denote Fermi wavenumber and velocity.
This Fermi energy (= EF ) is most important concept, which is often used in the condensed matter physics.
But unfortunately, there are NO concrete physical images in these concepts.
(Fig.16) Fermi energy is very vague concept.
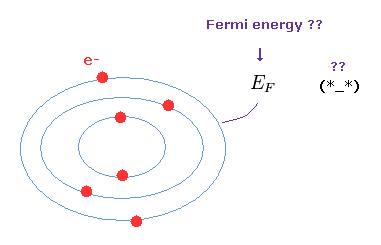
Orbitals become occupied in order from the lowest energy levels.
Each orbit contains two electrons due to Pauli exclusion principle.
The highest energy level of outer orbital is called "Fermi level ( energy )".
So these electrons in Fermi level cannot enter inner orbitals, which are already filled with other electrons.
(Eq.4) Approximate expressions.
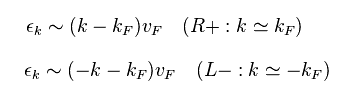
Here we define like Eq.4.
Energy εk is a square of wavenumber "k"
So there are two patterns (= ± k ) in one energy ε.
In Eq.4 upper, this "k" is close to +kF, and in Eq.4 lower, this "k" is close to -kF.
Here, sign of ± is also expressed as R = +, and L = -.
(Eq.5) Definitions of density ρ
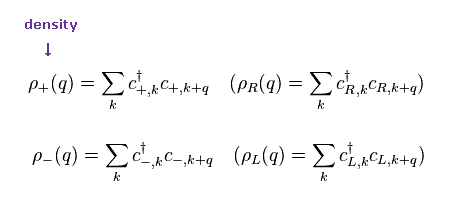
Here they define density operator ρ like Eq.5.
When the energy is close to Fermi energy, "k" inside ρ+ = ρR is close to +kF.
( On the other hand, "k" inside ρ- = ρL is close to -kF. )
(Eq.6) Strange commutation.
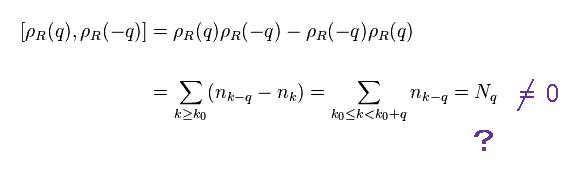
As you see Eq.5, this density ρ consists of two fermions, so this behaves like "boson".
Even when momentum "q" is different from "-q", commutator of these ρ operators doesn't become zero. Why ?
This is strange.
(Eq.7)
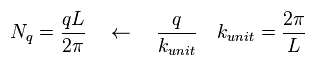
In Eq.6, Nq is defined like Eq.7.
"q" is momentum, and "2π/L" is unit of wavenumber.
Substituting Eq.5 into Eq.6, and using anticommutating relation of Eq.2, we get Eq.8.
(Eq.8)
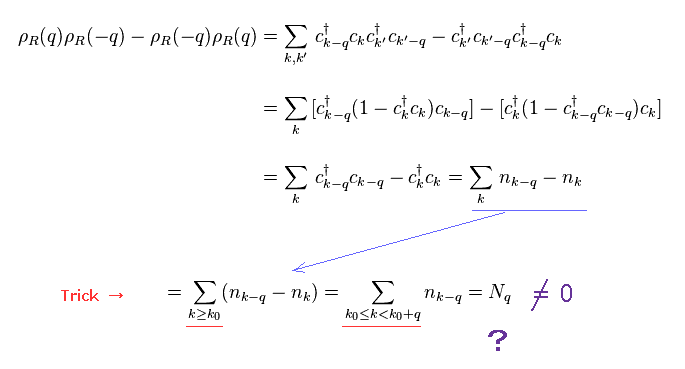
In Eq.8, "n" (= c†c ) means number operator.
Suddenly, they change number operator into just "number" (= Nq ) in Eq.8. This is clearly a trick.
The important point is that they define the lowest wavenumber as k0.
This is completely different from usual relativistic quantum field theory, which includes all wavenumbers (= momentums ) for Lorentz symmetry.
As a result, nk-q contains excessive wavenumber between k0-q and k0, which gives the difference of Nq.
But as you notice, this method doesn't define upper wavenumber.
Only lower limit is considered, This is strange.
(Eq.9)
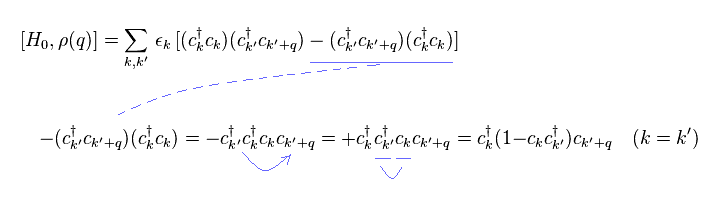
Here we consider commutation of Hamiltonian (= Eq.1 ) and ρ (= Eq.5 ).
For anticommutaion of "c", when c moves its neighbor, minus sign is added.
When c moves two operators, the sign is unchanged.
(Eq.10)
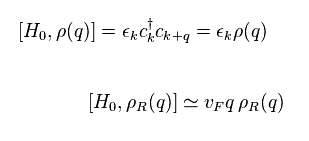
From Eq.9, we get Eq.10.
Eq.4 and ε = vFk = vFq are used.
(Eq.11)
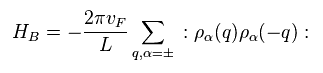
Here, they define new Hamiltonian like Eq.11.
There are NO reasonable reasons why they suddenly introduce this Hamiltonian.
(Eq.12)
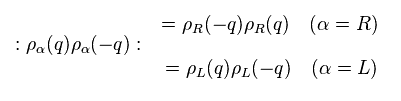
Of course, this is completely artificial definition.
Two fermions (= cc ) form one boson (= b ), so, they define new bosons (= b ) like Eq.13.
(Eq.13)
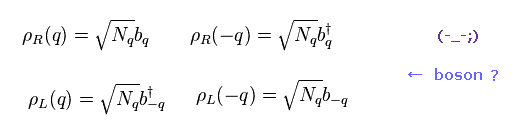
So they like to create new unreal bosons only for math tools.
This is what the present condensed-matter physics is.
Using new Hamiltonian of Eq.11 and relation of Eq.6, commutator of HB and ρ becomes
(Eq.14)
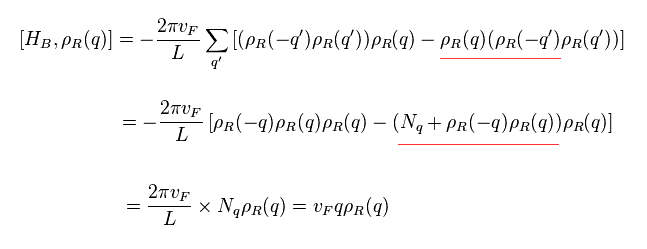
The result of Eq.14 is just equal to Eq.10, though their Hamiltonian (= H0 and HB ) are completely different forms.
But they suddenly accept new ( wrong ) equation of
(Eq.15) Wrong equation.
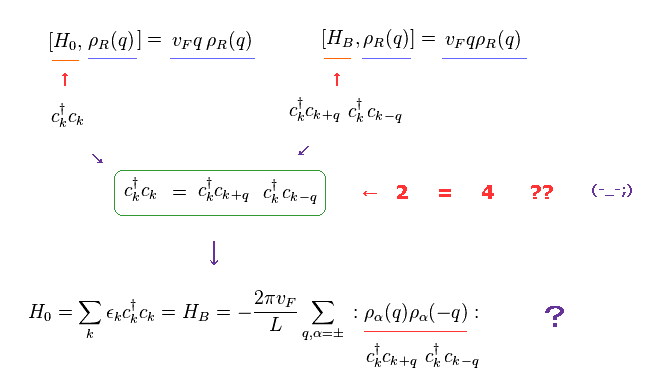
Commutation between Hamiltonian and ρ gives the same result, So these different Hamiltonian can be the same ?
As you see Eq.15, H0 contains only two operators (= c†c ).
On the other hand, HB contains as much as four operators (= c†cc†c ).
So the equation of H0 = HB is completely wrong.
But this wrong equation is indispensable for getting ( unreal ) quasiparticles of Spinon, Holon, and spin Peierls.
(Eq.16) Application of Wrong equation.

Using the wrong equation of Eq.15, they got the quasiparticles of Spinon and Holon.
At first glance, the equation of Eq.16 is unreasonable.
H0 means density, on the other hand, HB is density × density.
Here they choose this density × density form.
( In Eq.16, negative sign is omitted. )
(Eq.17)
In Eq.16, σ means "up" or "down" spins.
(Eq.18) Separation of one particle into Spin and Charge ??
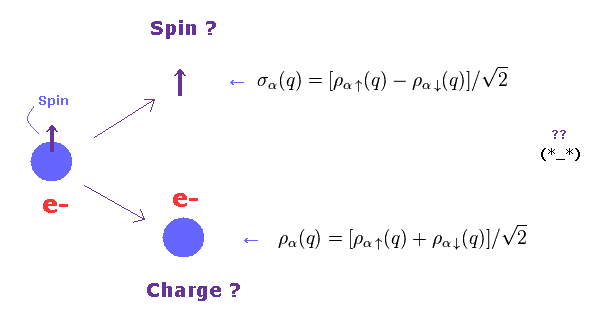
In Eq.18, the sum of "up" and "down" spin particles means total charge (= ρα ).
And the difference between "up" and "down" spin particles means spin magnetic moments (= σα )
(Eq.19)
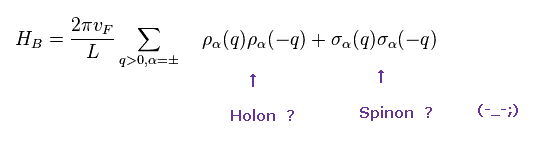
Substituting Eq.18 into Eq.19, we can get the Hamiltonian (= HB ) of Eq.16.
This is the reason why they insist Eq.19 means the separation into spin (= spinon ) and charge (= holon ).
But as you see, these are just abstract math operators, and have NO physical properties at all.
Of course, it is impossible to separate one elementary particle into "spin" and "charge".
As shown on this site, they just observe some photoemission spectroscopy.
By linking these results to some artificial definitions, they just insist spin and charge are separated.
This is what the latest condensed matter physics is. (= NOT science at all ).
(Eq.20)
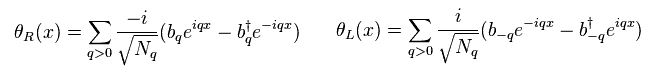
Here θ is defined like Eq.20 using new bosons of Eq.13.
Again, they introduced other new bosons (= Φ ) like Eq.21.
(Eq.21) Again, new bosons ?
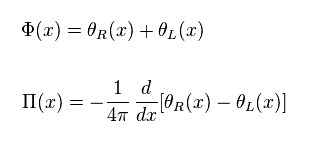
You can find these Φ and Π satisfy usual commutation relation of Eq.22, using Eq.13, Eq.20 and Eq.21.
So they insist new bosons appear, again.
(Eq.22) Commutator = new bosons ?
where we use
(Eq.23)
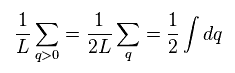
And you find Hamiltonian (= HB ) of Eq.11 can be expressed using Eq.21, like Eq.24.
(Eq.24) Hamiltonian using new bosons ?
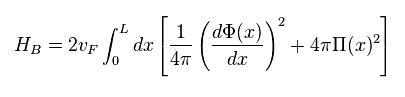
As you see, the present condensed matter physics tries to take advantage of various new bosons as mathematical techniques.
There are no physical meanings here, they are going away from reality.
(Eq.25)
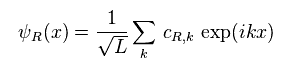
They define fermions ψ like Eq.25.
As you see, there are extremely many artificial definitions in the current quantum theory.
Commutator of b ( see Eq.13 and Eq.5 ) and ψ (= Eq.25) becomes
(Eq.26)
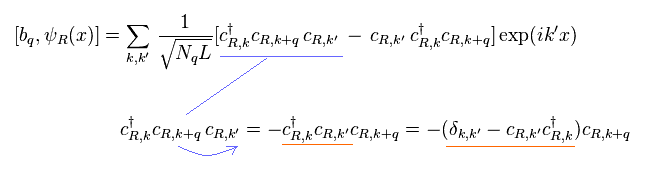
where they define
(Eq.27)
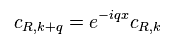
Redline of Eq.26 is anticommutation of Eq.2.
As a result, we have
(Eq.28)
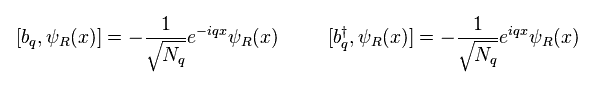
(Eq.29) Coherent states.
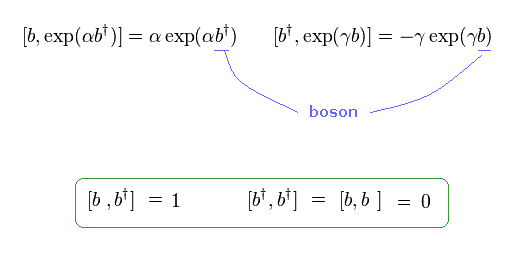
When b and b† are bosons and satisfy commutation relation, the equation of Eq.29 holds.
Here the formula of Eq.30 is used.
(Eq.30)
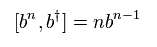
Comparing Eq.28 and Eq.29, they consider red and blue parts of them are just equal to each other.
This is very forcible interpretation, and just wrong.
(Eq.31)
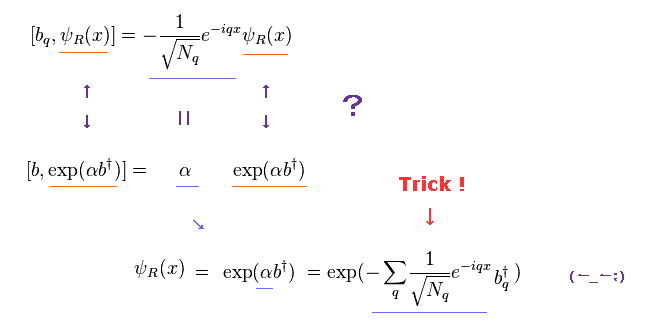
Unfortunately, this equation is NOT true.
Finally, using both parts of Eq.29, they define
(Eq.32)
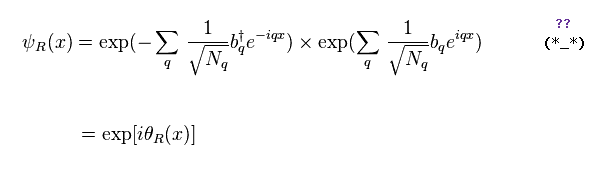
where θR is Eq.20.
Of course, equation of Eq.32 ( or Eq.31 ) is wrong.
Because
(Eq.33)
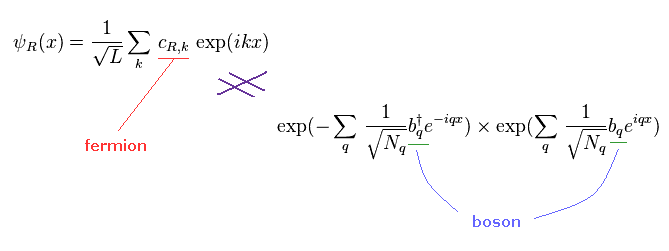
Bosons cannot be fermions, no matter how many bosons are combined.
So the current condensed matter physics is based on completely wrong assumptions both in mathematics and physics.
(Eq.34)
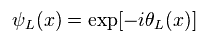
In the same way, we get Eq.34.
From Eq.32, Eq.34 and Eq.21, we get
(Eq.35)
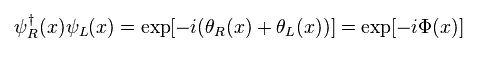
As a result,
(Eq.36)
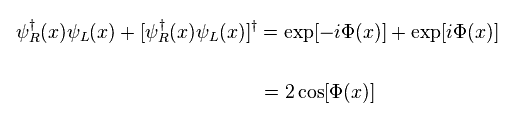
where we use
(Eq.37)
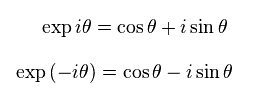
This is just mathematical trick.
They have already become out of touch with reality.
(Fig.16) "Spin Peierls" transition really means "Spin" ?
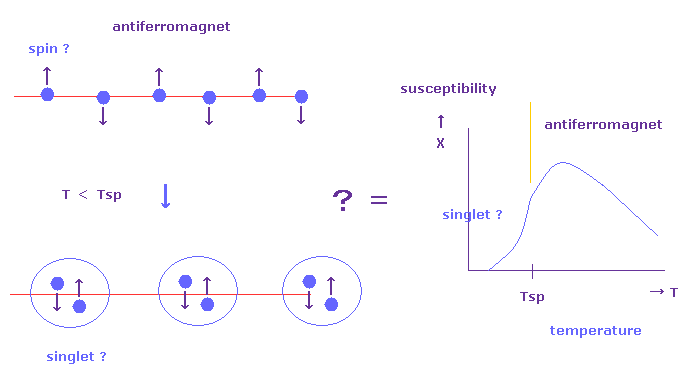
In spin-Peierls transition, antiferromagnet such as CuGeO3 becomes spin-singlet non magnet (= dimerization ) below some critical temperature (= Tsp ). See also this site
Of course, we cannot see unrealistic spin directly.
They just imagine these states only from magnetic susceptibility (= χ ) of Fig.16.
In antiferromagnet, susceptibility responding to external magnetic fields is much larger than singlet state, they insist.
In singlet state, two "up" and "down" spin atoms are tightly bound to each other ( of course, they cannot see these states directly. )
But they NEVER explain what these strong binding forces between spins really are.
As shown on this page, (anti) ferromagnetic energy is much stronger than spin magnetic dipole interaction.
(Fig.17) Spinless fermions are necessary ?

Surprisingly, the spinless fermions are necessary for spin-Peierls transition, they insist.
( See this site or this site )
Even in unrealistic supersymmetric theory, spinless fermions don't exist.
So from the beginning, these theories are inconsistent.
(Eq.38) Nonlocal superposition of spinless fermions !?
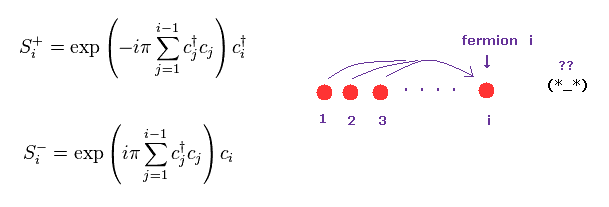
They define spin operators such as S+ and S- like Eq.38.
In Eq.38, ci means spinless fermion at the atomic position of "i".
Unfortunatelly, these spin model can treat ONLY one dimensional spin system for mathematical reason.
Even in simple one-dimension, they have to rely on some appoximations.
Surprisingly, these spin operators contains many other atomic spins.
Spins at different positions from 1 to i-1 influence spin at "i" (= nonlocal interactions ).
Unfortunately we cannot describe these nonlocal spinless fermions usin real objects.
(Eq.39)
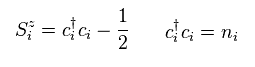
They define Sz component like Eq.39.
As you see in Eq.38 and Eq.39, these fermions (= c ) have NO spins, so they can be used as the common fermions in different spin component operators.
And of course, these definitions are completely artificial.
(Eq.40)
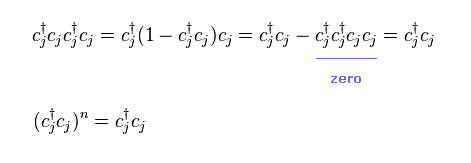
Fermions obey anticommutation relation of Eq.2.
So two adjoining same operators like "cc" and "c†c†" become "zero".
As a result,
(Eq.41)
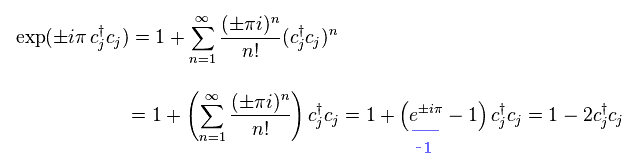
Using Eq.41, Eq.38 becomes
(Eq.42)
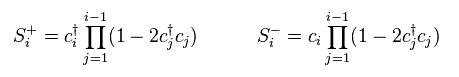
Sx and Sy components of spin can be expressed like Eq.43.
This transformation is called "Jordan -Wigner transformation"
(Eq.43)
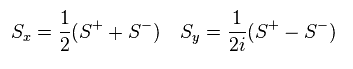
(Eq.44) XXZ one-dimensional spin model.
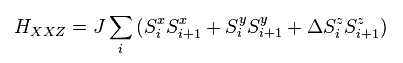
XY model is so simple that we can solve it completely.
But XY model with no z component spin cannot describe real atomic states.
XXZ Heisenberg spin model is often used in spin Peierls transitions.
The problem is that this XXZ model cannot be solved, so we have to rely on some rough approximations and numerical calculation.
(Eq.45)
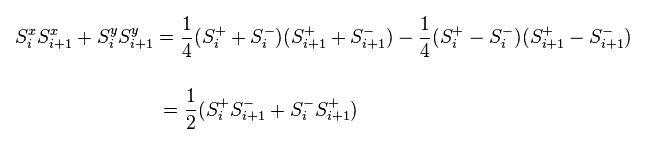
Substituting Eq.43 into Eq.44, we obtain Eq.45 ( x, y parts ).
And using the definition of Eq.42 and anticommutation relation, we have
(Eq.46)
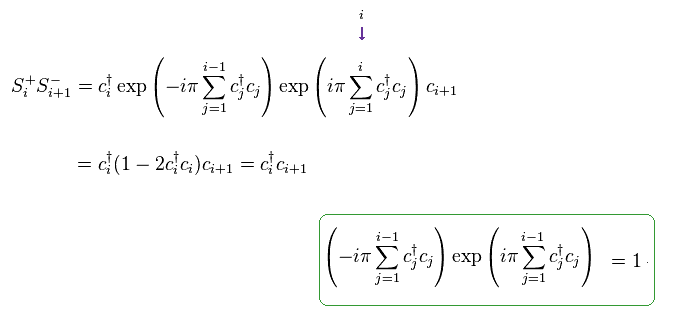
and
(Eq.47)
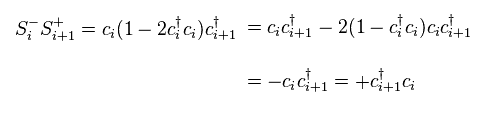
Substituting Eq.39, Eq.46 and Eq.47 into Eq.45 and Eq.44, we have
(Eq.48)
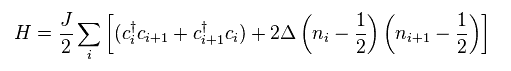
In spin Peierls transition, uniformity of interatomic length needs to be broken.
So we have to adopt the following Hamiltonian.
(Eq.49)
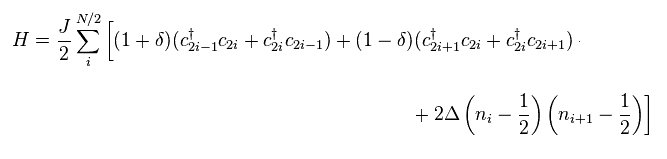
In Eq.49, interatomic length at odd sites are different from that of even sites.
As you see, they just intentionally change the form of Hamiltonian to fit experimental results.
So these models are NOT natural results
(Eq.50)
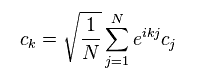
(Eq.51)
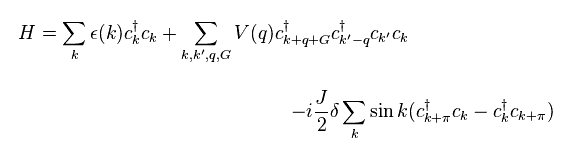
where G= 2π × n and
(Eq.52)
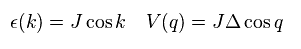
In Eq.52, we need to depend on artificial transformations like Eq.15, Eq.24 and Eq.36.
As a result, Hamiltonian of Eq.51 becomes
(Eq.53)
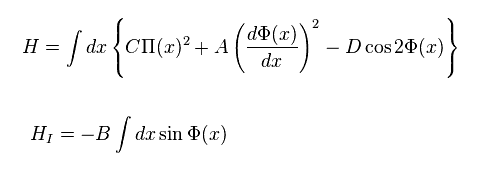
where
(Eq.54)
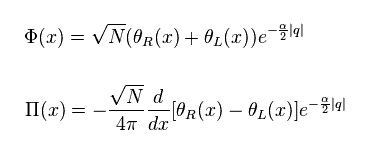
See Eq.20.
And
(Eq.55)
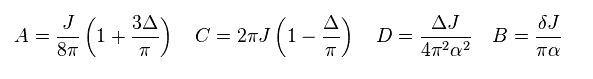
These methods are also called "phase Hamiltonian".
Fermi wavenumber is defined as
(Eq.56)
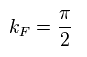
The problem is that these forms are inconsistent with other spin wave theories.
So they artificially change the coefficient of Eq.55 into
(Eq.57)

where
(Eq.58)
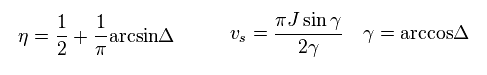
This is one of manipulations.
Here we consider the change from π/2,
(Eq.59)
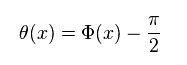
We treat Hamiltonian of Eq.53 as variational function like
(Eq.60)
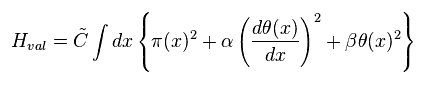
Coefficients α and β as variational parameters.
So these are free parameters, we can adjust freely.
Fourier componets of θ and π are
(Eq.61)
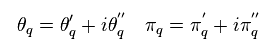
Substituting Eq.61 into Eq.60, and suddenly they define new artificial bosons (= "a", and "b" ) like
(Eq.62) New boson's generation. ← mathematical trick, again.
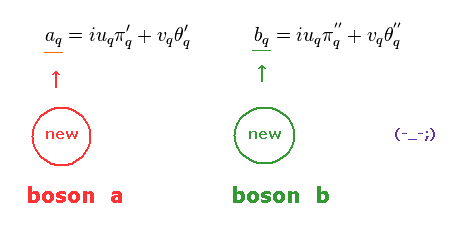
Of course, these bosons are unreal quasiparticles.
But they define new vacuum based on these artificial bosons like Eq.63,
(Eq.63)
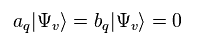
Applying vacuum of Eq.63 to Hamiltonian of Eq.60,
(Eq.64)
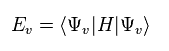
The result of energy is
(Eq.65)
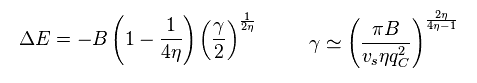
In antiferromagnet, Δ ( see Eq.44 ) is positive, and η ( see Eq.58 ) are
( These Δ and η are free parameters we can manipulate. )
(Eq.66)
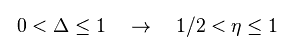
From Eq.65, index of B ( considering also B inside γ ) is
(Eq.67)
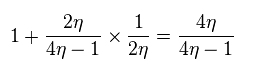
From Eq.55, B is proportional to δ (= difference of coupling constants at odd and even sites ).
Supposing this coupling constant between spins are proportinal to some variables λ and distortion (= u ) of each atomic positions, the energy of Eq.65 can be expressed as
(Eq.68)
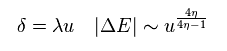
Here we define η = 1 (= artificial choice, again ).
(Eq.69)
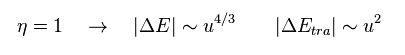
When each distortion (= u ) of atomic positions is very small, the decrease of energy (= 4/3 power of "u" ) is larger than the increase of distortion energies (= a square of "u" ), they insist.
But we don't know the value of λ of Eq.68.
And as you see, they use various artificial definitions and quasiparticles.
Unfortunately, these theories are very far from reality.
(Eq.70) Boltzmann factor is classical mechanics.
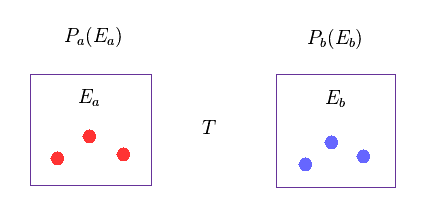
It is known that various classical mechanical theories apply in actual phenomena, and they are basis of the current condensed matter physics.
For example, Borltzmann factor, Drude's conductivity and Curie-Weiss law..
Here we derive Boltzmann factor (= exp(-βE) ) using classical mechanics.
In Eq.70, Ea and Eb are energies of each A and B independent systems.
Probabilities of these states are Pa and Pb, respectively.
T is temperature.
(Eq.71)
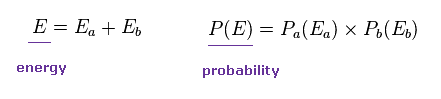
In Eq.71, E and P(E) are the total energy and probability.
Differentiating P(E) of Eq.71 with respect to Ea, we have
(Eq.72)
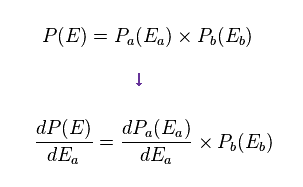
We also express this differentiation like
(Eq.73)
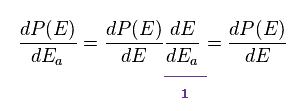
Eq.72 is equal to Eq.73.
(Eq.74)
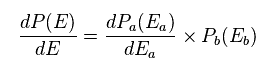
Dividing both sides of Eq.74 by "P" of Eq.71, we have
(Eq.75)

In Eq.75, left side consists only of the variable "E", and right side consists only of Ea.
Considering two variables are independent from each other, both sides need to be some constant (= -β ).
As a result,
(Eq.76)
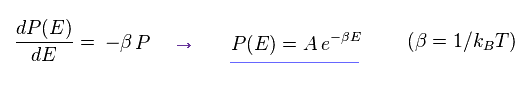
This is a famous Boltzmann factor.
This is completely classical mechanics.
(Eq.77)
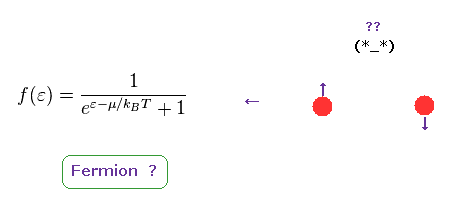
As shown on this page, Fermi statistics becomes like Eq.77.
In Eq.77, ε is energy, and μ is Fermi energy.
As far as I see various methods in condended matter physics, they don't use Fermi statistics of Eq.77 as it is.
They always change Eq.77 into very rough approximation.
So we have NOT yet prove Eq.77 is really correct.
(Eq.78)
Here we consider the extremely low temperature ( T → 0 ).
When the energy (= ε ) of the system is higher than Fermi energy (= μ ),
(Eq.79)
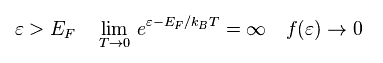
The probability f(E) of Eq.77 becomes zero in the limit of T → 0.
And when the energy is lower than Fermi energy,
(Eq.80)
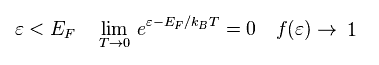
f(E) becomes "1" in the limit of T → 0.
So they insist Fermi particles fill orbitals lower ( not upper ) than Fermi energy.
But this approximation is so rough that we cannot judge whether Eq.77 is really correct or not.
(Eq.81)
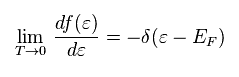
Eq.81 is Sommerfeld expansion.
δ( ) is Delta function.
Again, this is very rough approximation.
(Eq.82)
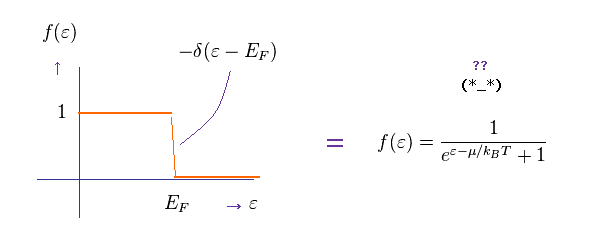
Seeing the acute transition from Eq.80 (= 1 ) into Eq.79 (= 0 ) at the point of Fermi energy, you can understand the delta function of Eq.82.
( At ε = EF, this delta function becomes infinity. )
On the other hand, Planck constant (= quantization of de Broglie wave ) and Boltzmann factor had been proved to be correct.
(Eq.83) Planck constant and Boltzmann factor are correct.
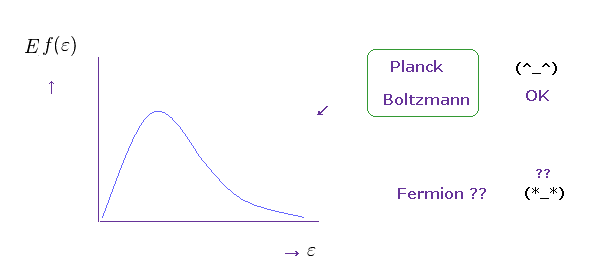
(Eq.84)

"Phonon" is the most important concept in the current condensed matter physics.
Hamiltonian of this phonon becomes like Eq.84.
Last term of Eq.84 means the interaction between phonon (= b ) and electron (= c ), they insist.
As you see, these interactions are too abstract to be applied to actual complicated phenomena
(Eq.85) Coupling constant.
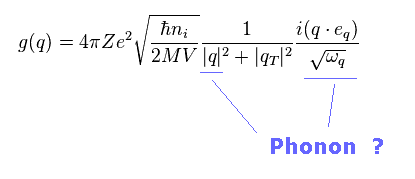
Eq.85 is coupling constant between phonon and electron.
Unfortunately, these parameters are just virtual, and don't express real phenomena.
(Eq.86)
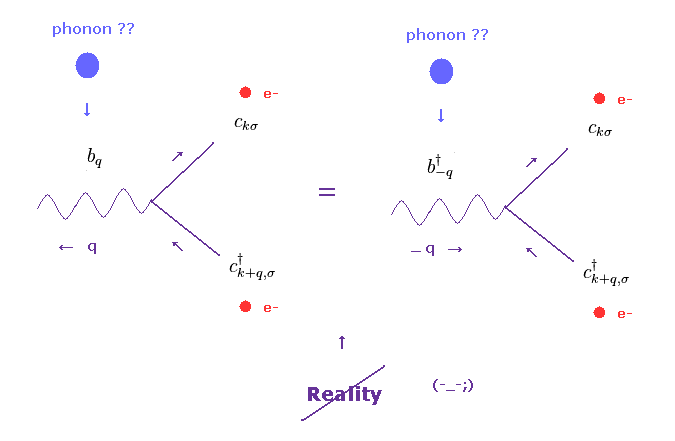
The meaning of the phonon's interaction term (= last term of Eq.84 ) is like Eq.86.
In Eq.86 left, the electron with momentum of "k+q" gives the energy (= q ) to phonon (= b ), and becomes "k".
( "bq" means phonon with "q" is annihilated. )
The maeaning of Eq.86 right is the same as Eq.86 left.
"b-q†" means phonon with the momentum of "-q" is created.
(Eq.87) Imaginary time is indispensable.

In fact, the current condensed matter physics completely depends on virtual "imaginary" time for phonon's transition.
So these theories lack reality from the beginning.
Here we explain how this imaginary time (= - i τ ) is used in phonon's Green function.
Usual form of operator in Heisenberg (= interaction ) picture is
(Eq.88)
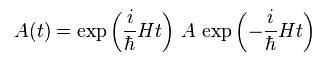
Here they suddenly change real time (= t ) into imaginary time (= τ ) like
(Eq.89)
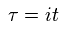
Substituting Eq.89 into Eq.88, we have
(Eq.90)
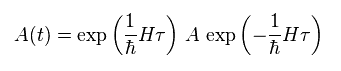
Green function is propagator, which shows how the states will change with time.
In this thermal Green function, they see ONLY the direction of imaginary time.
( Though we want to know how the states change with real time. )
(Eq.91)
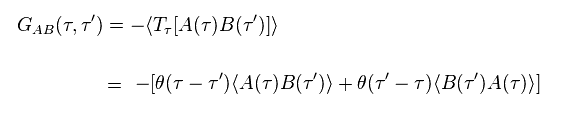
In Eq.91, θ( τ - τ' ) is step function.
( When τ - τ' > 0, this θ is "1", when τ - τ' < 0, this θ is "0". )
Two operators are in time order (= Tr, right is before, left is after. )
(Eq.92)
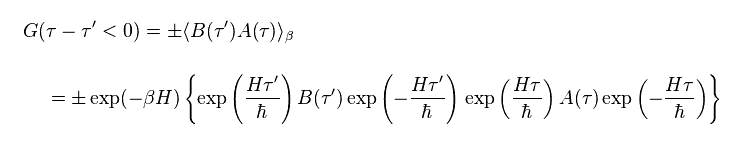
Eq.92 picks up only the last term of Eq.91.
In fermions, commutating gives negative sign. ( ± : + is boson, - is fermion. )
At finite temperature, the probability is given by Boltzmann factor (= exp(-βH) ) × Green function, as shown in Eq.92.
(Eq.93)
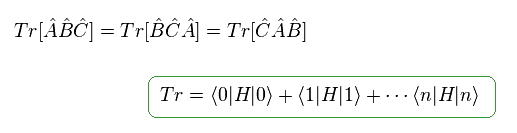
When we consider some Hamiltonian (= H ), eigenstates on left and right sides are the same.
If we use some matrix, this results correspond to trace of that matrix.
And the order of these matrices can be circulated like Eq.93 (= trace ).
Using Eq.93, Eq.92 becomes
(Eq.94)
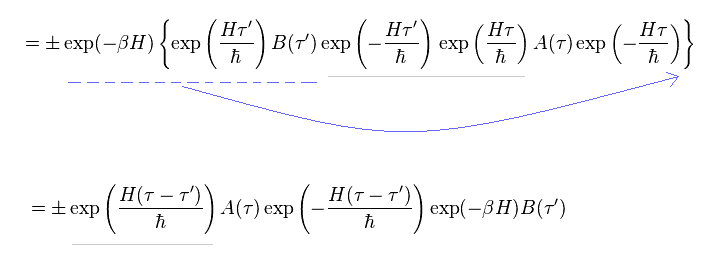
In Eq.94, exponential functions containing H can be commuted.
Three operators on the left side are transferred to the right.
And adding two exponential functions (= exp(-βH) exp(βH) = "1" ) to Eq.94 from left side, we have
(Eq.95)
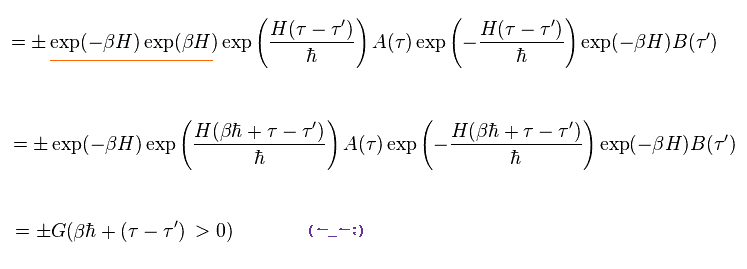
Like Eq.95, imaginary time τ-τ' is changed into βħ + τ-τ', after incorporating Boltzmann factor into them.
The important point is that, we need to adopt artificial condition of Eq.96.
(Eq.96)
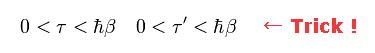
Under the condition of Eq.96, Green funtion become the same periodically at the interval of imaginary time βħ, they insist.
But as you see, we want to know how states change with "real" ( NOT imaginary ) time.
So these operations are just mathematical trick with NO reality.
(Eq.97)
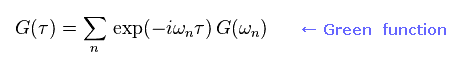
Eq.97 is Fourier series of this Green function.
Considering periodicity with time, these frequencies (= ω ) become discrete like
(Eq.98) This is just for math trick.
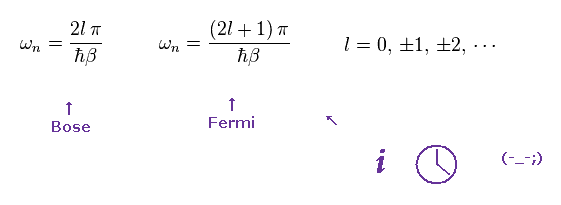
In Fermion's Green function, negative sign is added, when two operators are exchanged.
So these frequencies become odd number × π in fermions
There are NO physical images in these tricks.
This is what the latest condensed matter physics really is.

2014/1/11 updated. Feel free to link to this site.