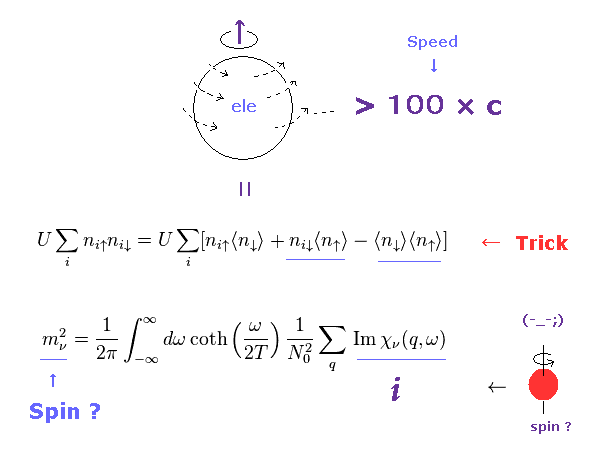
Top page (correct Bohr model including helium. )
"Spin" is an illusion, again.
BCS theory makes grave mistakes.
(Fig.1) "Spin" itself is unreal → various artificial tricks were produced.
As shown in this page, spin itself has NO reality with respect to faster-than-light spinning speed and so on.
So all they can do is use very abstract mathematical operators to describe unreal "spin".
Of course, if spin itself is unreal concept, Pauli exclusion principle and spin-orbit interactions cannot be expressed correctly using "spin".
These abstract mathematical operators can be easily and intentionally manipulated to fit experimental results.
In this page, we show various artificial tricks about "spin", and the fact they must rely on these tricks proves "spin" doesn't really exist.
(Fig.2) Magnetic susceptibility χ and temperature T.
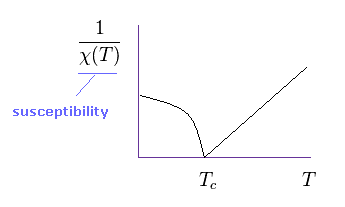
The Curie-Weiss law describes the magnetic susceptibility χ of a ferromagnet in the paramagnetic region above the Curie temperature (= Tc ).
It is known that Curie-Weiss law holds in various materials.
But of course, this law is rough approximation, so actual materials show much more complex property.
The important point is that this universal law is based on classical mechanics.
Because the year of 1907, when this law is produced, is before quantum memchanics was born.
(Eq.1) Classical magnetic moment ?
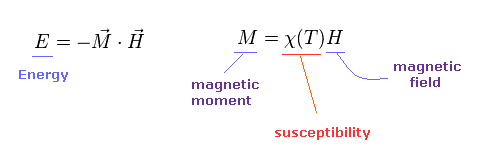
First, P. Langevin think about each atom of metal has some ( classical ) magnetic moment (= M ) in 1905.
Under the external magnetic field (= H ), the magnetic energy becomes "-MH".
And the magnetic susceptibility (= χ ) can be gotten, dividing magnetic moment by magnetic field ( χ = M / H ).
(Eq.2) Curie law by Langevin.
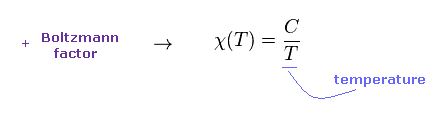
Using Boltzmann distribution (= e-E/kT ), he can get the Curie law approximately.
If we measure Curie constant C in experiments, we can know approximate magnetic moment "M" in various metals.
(Eq.3) Curie-Weiss law.
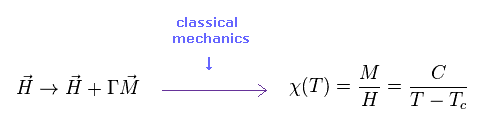
In 1907, Weiss considered the effects among other atoms, too.
"ΓM" is the internal magnetic field from other atoms.
As a result, the relation between magnetic susceptibility and temperature becomes like Eq.3.
It is known this Curie-Weiss law holds in various metals.
And this important law can predict phase transition between ferromagnetism and paramagnetism (= above Tc ).
Stoner-Wohlfarth theory can predict properties such as the relation between magnetic susceptibility, temperature.
See also
this (p.84).
But as shown in this site (p. 5-6), It is known that values predicted by Stoner theory are inconsistent with various experimental results especially in paramagnetic states.
(Eq.4) Magnetic moment M ? Spin ? in SW model.
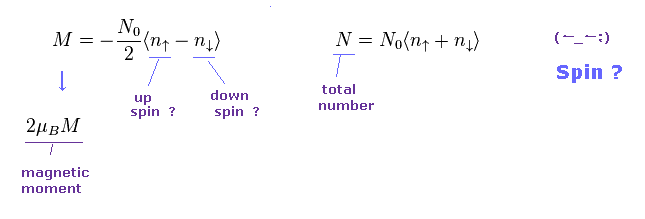
In the current condensed matter physics, all they can do is rely on very abstract operators to express each particle.
In Eq.4, the difference between "up" and "down" spin electrons causes magnetic moment (= M ), they insist.
( Of course, these spins are only mathematical symbols without concrete images. )
The total number of atom (= N ) is the sum of up and down spins.
(Fig.3) There are NO choices other than "Spin" as magnetic moment. "Spin" = God !?
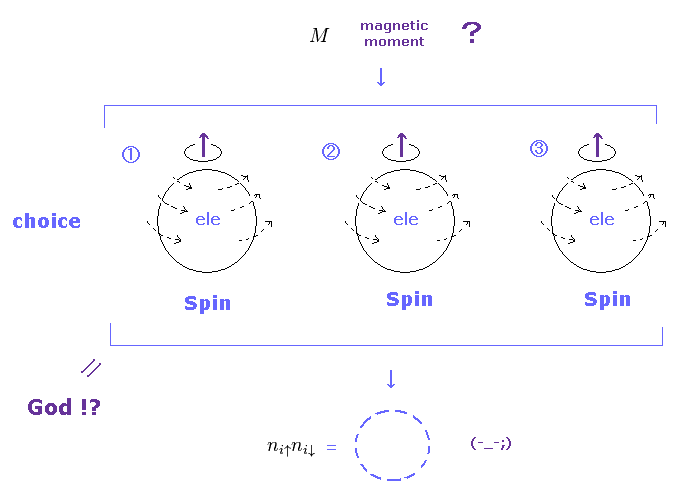
In the present quantum theory, they blindly believe unreal spin as preconditions, from the beginning.
There are NO other alternatives accoording to the current condensed matter physics.
This is very unreasonable and forcible idea.
This is the main reason why we often see the word of "spin" in various ( top ) journals, though they do NOT try to say what spin really is, forever.
(Eq.5) Number of up and down spins.
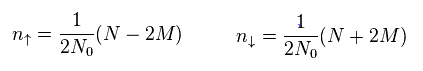
From Eq.4, we get each number (= n ) of up and down spin particles like Eq.5.
(Eq.6) Spin model ?
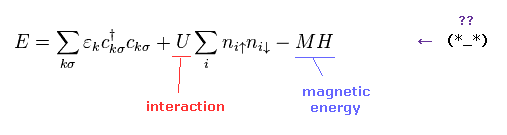
Hubbard model is often used as effective Hamiltonian, which contains two kinds of interactions.
The second term is magnetic interaction among electrons, and M and H of the third term are total magnetic moment and external magnetic field, respectively
( So this third term is total magnetic energy. )
But as you see Eq.6, again, this model of condensed matter physics is too abstract to describe various complicated phenomena.
Furthermore, they just adjust these parameters such as interaction "U", by hand.
(Eq.7) Number operator.
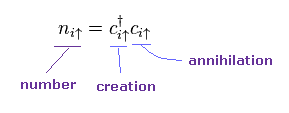
Like usual quantum field theory, the number operator (= n ) consists of creation (= c† ) and annihilation (= c ) operators of ( conduction ) electrons.
This is only "abstract" math symbol, as I repeated many times.
(Eq.8) Anticommutation.
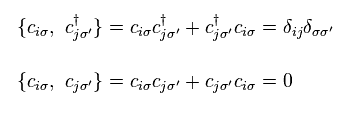
Fermions need to satisfy anticommutation of Eq.8.
You need to know this relation belongs only to mathematical world.
Because actual electron's shape is different from math operator
(Eq.9) Anticommutation = Pauli exclusion principle ??
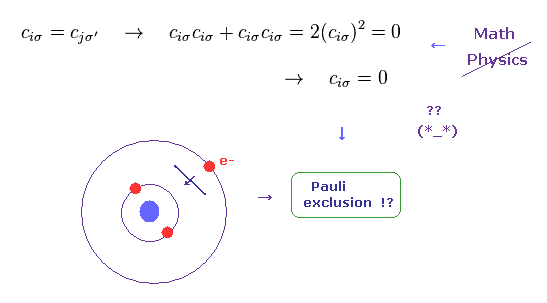
According to the present quantum field theory, the origin (= force ) of Pauli exclusion principle is the property of anticommutation among operators.
So even if you ask some physicists about the repulsive force of this Pauli exclusion, they cannot give clear answers at all.
They just show very abstract math, which is too vague and the main factor obstructing the development of science.
If these operators satisfy anticommutation, they (= "c" in Eq.9 ) becomes zero, when c = c, because cc + cc = 0.
This is the origin of Pauli exclusion, they insist.
Can you understand this explanation well ?
(Eq.10) Artifical Trick.
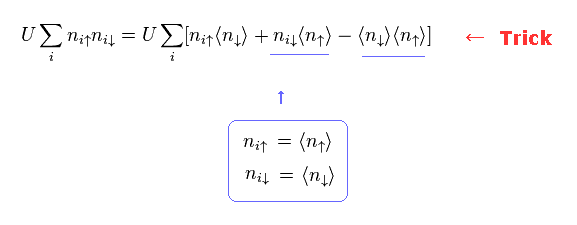
Here they change the second term of Eq.6 like Eq.10.
This is clearly artificial trick to get some experimental results.
After splitting the specific term into three terms, they just choose convenient terms for their theory.
Trick of BCS theory.
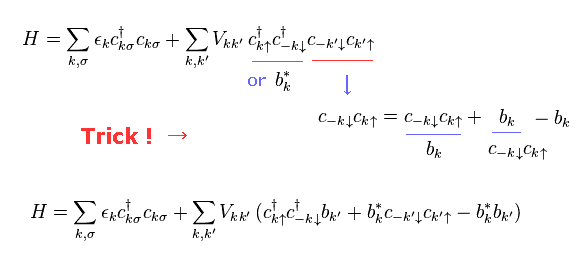
Trick of Eq,10 is very similar to BCS theory.
( See Eq.19' of BCS theory. )
Also in BCS, after they add two excess terms (= b - b ), they pick up only convenient terms.
This is the truth of the current "spin" theories.
Even after you know these serious facts, can you still believe "spin" ?
(Eq.11)
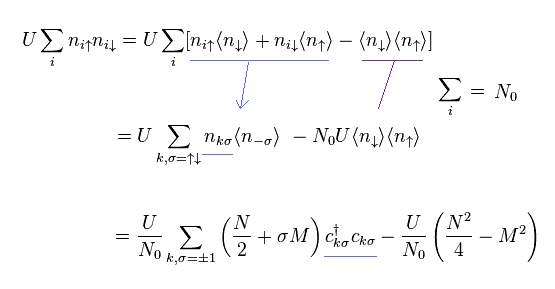
Using Eq.5, Eq.7 and Eq.10, we obtain Eq.11.
(Eq.12)
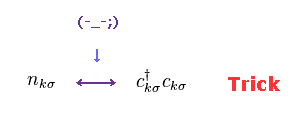
In Eq.11, they choose which form is better, "n" or "c†c" in each term.
This is also one of intentional manipulations.
(Eq.13)
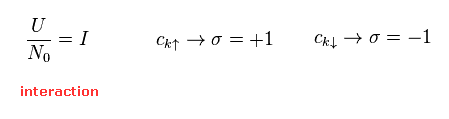
In Eq.11 the notations of Eq.13 is used.
When "c" is "up" spin, σ is "1".
When "c" is "down" spin, σ is "-1".
(Eq.14)
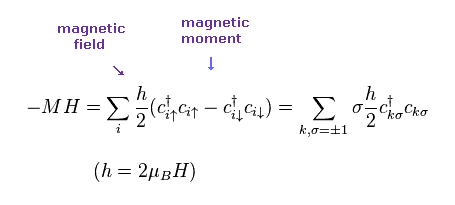
Using Eq.4, magnetic moment and energy become Eq.14.
Here "h" is 2μBH ( "H" is external magnetic field ).
(Eq.15)
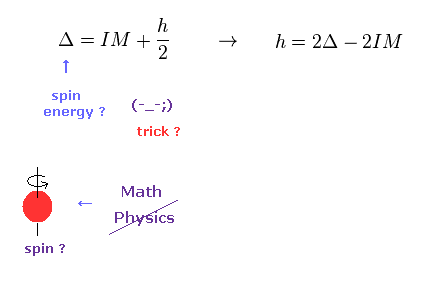
From σ terms of Eq.11 and Eq.14, spin energy Δ can be gotten, they insist.
But as you see Eq.11, they just pick up conveninet terms for Δ
This is not a natural result at all.
( Actually, other terms are neglected. )
(Eq.16) Free energy of SW model.
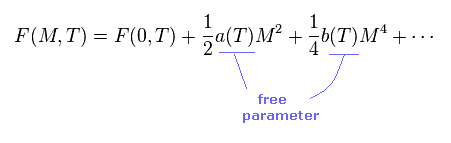
In SW model, free energy F(M,T) is a function of magnetic moment (= M ) and temperature (= T ).
Terms of odd order with respect to "M" vanish.
Coefficients a(T) and b(T) cannot be gotten from theory itself.
These are free parameters, which must be decided based on experiments.
(Eq.17) Magnetic field "h".
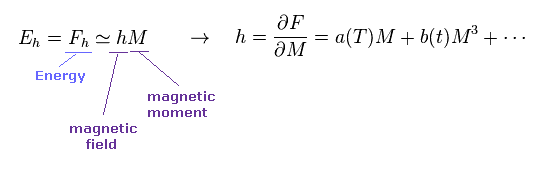
From Eq.16 and Eq.17, magnetic field (= h ) is obtained by differentiating free energy (= F ) with respect to the magnetic moment (= M ).
(Eq.18)
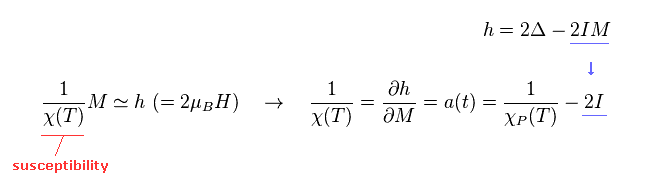
Magnetic moment (= M ) is equal to h × χ (= susceptibility ).
So the reciprocal of χ is gotten by differentiating "h" with respect to "M".
Here they add "IM" term of Eq.15 to this χ.
This "IM" term was gotten by artificial trick of Eq.11.
And the magnitude of interaction (= I ) can be decided only from experiments ( NOT theory itself ).
(Eq.19)
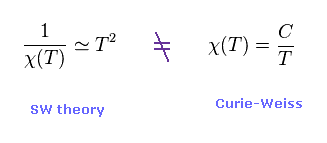
After expanding equations in powers of (kT) and using some approximations, SW theory can get the relation of Eq.19.
This is inconsistent with Curie-Weiss law.
(Eq.20) Ni susceptibility doesn't satisfy SW model.
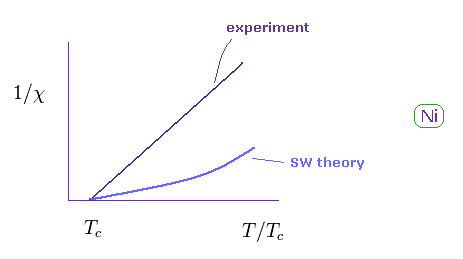
As shown in Eq.20, this SW model does NOT agree with experimental results of various atoms.
( Some atoms satisfy SW theory. )
Of course, SW model can only do rough estimation.
The important parameters such as a(T), b(T), and "I" need to be decided only from experiments.
(Fig.4) DFT in condensed matter physics is only "rough" approximation.
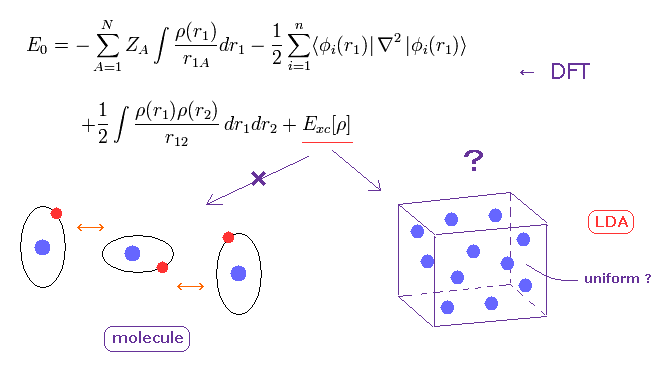
Density functional theory (DFT) is often used in band calculation.
The important point is that DFT cannot determine very important part of exchange-correlation energy (= Exc ).
They often use local density approximation (LDA), which uses very rough approximation of uniform electron gas.
Of course, electron distribution of actual metals are NOT uniform.
So they add some appropriate potential to this LDA.
Metals contain infinite atoms, so pure ab-initio methods are impossible.
They find and choose the most convenient potentials to give experimental results.
In case of weak magnetic interaction, this estimation is much more difficult and speculative.
So the current band theory has NO power to predict actual energy without relying on some empirical values.
(Fig.5) Spin fluctuation ?

It is known that Curie-Weiss law hold in the paramagnetic phase of ferromagnet.
This phenomena cannot be explained by SW model.
So they tried to add other effects such as "spin fluctuation" to SW model, because there is ONLY unreal spin as choices in quantum mechanics.
This new thoery is called self-consistent renormalization (= SCR ) theory.
As I said many times, "spin" itself is completely unreal concept.
This means even all of the latest spin models lacks reality.
This SCR spin theory is a good ( bad ) example of these artificial tricks with respect to "spin".
So I decided to write about this SCR theory.
(Eq.21)
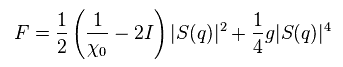
We use the coefficient a(T) of Eq.18 in free energy of Eq.16.
b(T) of Eq.16 is changed into "g".
F(0,T) term of Eq.16 is omitted.
As I said, the magnitude of interaction (= I ) cannot be gotten from these theories themselves.
S(q) is spin magnetic amplitude, they insist.
(Eq.22) Spin fluctuation ?
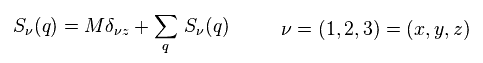
As shown in Eq.22, the main magnetic moment (= M ) is parallel to z axis.
The second term of Eq.22 is spin fluctuation.
A square of Eq.22 become
(Eq.23)
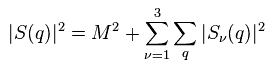
The fourth power of S(q) becomes
(Eq.24)
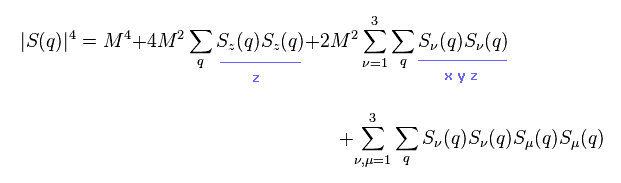
where odd ordered terms are omitted.
Substituting Eq.23 and Eq.24 into Eq.21, terms of M2 and M4 become
(Eq.25)
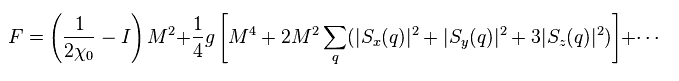
The relation of Eq.17 and Eq.18 are
(Eq.26)
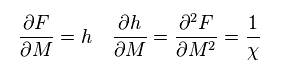
Differentiating Eq.25 twice with respect to M (= Eq.26 right ), the reciprocal of susceptibility χ becomes
( omitting M4 term )
(Eq.27)
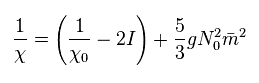
where
(Eq.28)
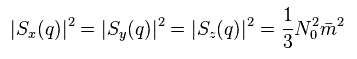
Here they use the most artificial trick.
They insist the density of each spin (= m2 ) is related to the imaginary part of the dynamical magnetic susceptibility through
(Eq.29) Spin = "imaginary" number ??
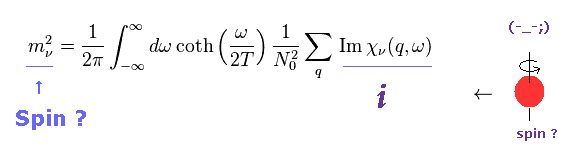
Of course, pure "imaginary" number "Im χ" is completely unreal concept.
Then why this unreal concept appears as spin density ?
Here we derive Eq.29 based on spin fluctuation theory.
According to quantum mechanics, Heisenberg relation between some operator (= spin S(t) ) and Hamiltonian H becomes like Eq.30.
( Here "B" is magnetic field, and "H" is magnetic energy. )
(Eq.30)
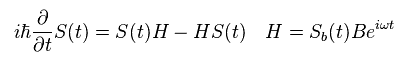
As I said in Eq.18, magnetic susceptibility (= χ ) is given, dividing ( spin ) magnetic moment (= S ) by magnetic field (= B ).
(Eq.31)
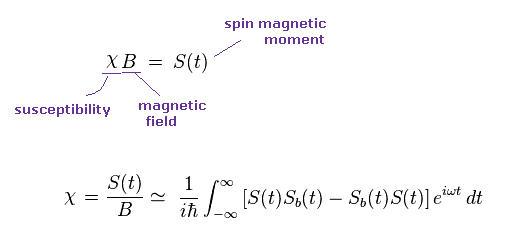
Hamiltonian H is proportional to particle's density.
In Eq,31, some coefficients are omitted.
In the second term of Eq,31, they suddenly use "imaginary" time of i/T.
Changing the time variable "t" into t' - i/T (= imaginary time ! Doesn't exist ),
(Eq.32) "Imaginary" time "i/T" is illusion ?
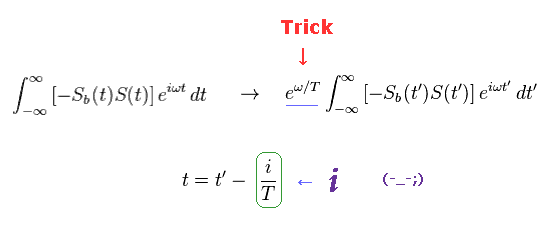
As a result, they can intentionally get an exponential function (= eωT, blue line ).
This is clearly unnatural manipulation to fit some experimental results.
While they introduced imaginary time in the second term, they keep the first term of Eq.31 as it is.
Summing the first and second terms of the right side in Eq.31, we have
(Eq.33)

The new exponential function appears in Eq.33 ( compare it with the original equation of Eq.31 ).
Next they change "minus" of Eq.33 into "plus" like
(Eq.34)
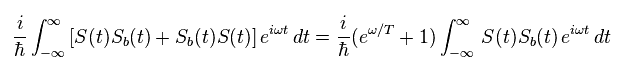
From Eq.33 and Eq.34, we get
(Eq.35)
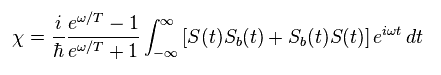
Using the following relation
(Eq.36)
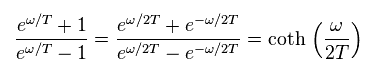
we have
(Eq.37)
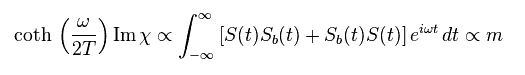
Due to imaginary number "i" of right side in Eq.35, this magnetic susceptibility χ becomes pure imaginary number !
So you easily find these values related to "spin" are completely unrealistic.
(Eq.38) "Imaginary" magnetic susceptibility (= Im χ ) is real ?
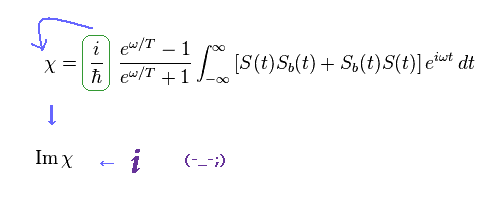
This is the truth of the latest spin theory.
The present physicists in condensed matter physics just play with mathematical tricks, going away from physical reality.
Probably you understand well why I often insist "spin" itself lacks reality.
Dividing coth term like
(Eq.39)
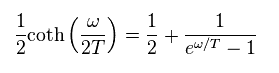
Spin density of Eq.29 becomes
(Eq.40)
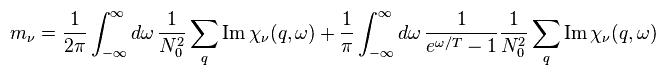
Here they pick up only the second term of Eq.40.
According to their spin theory, scattering cross section of neutron show some spin fluctuations like Eq.41.
(Eq.41) Neutron scattering really shows unreal spin ??
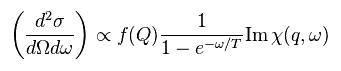
But of course, this interprettion is only speculation.
We cannot see spin fluctuations themselves directly. They just see neutron ( or light ).
And artificial manipulations such as imaginary time and susceptibility make you find these theories don't advance toward physical truth.
(Eq.41') Neutron scattering = spin wave ??
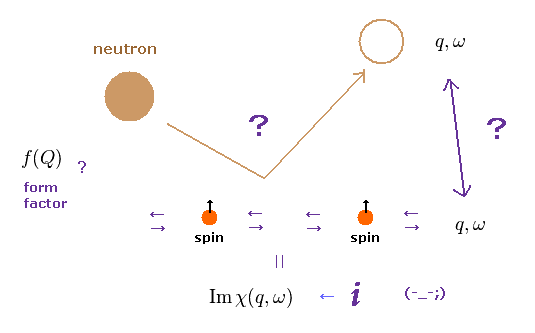
The important point is that the magnetic form factor f(Q) in Eq.41 includes various other effects.
So it is impossible that we know how imaginary spin wave influences this form factor.
They insist conduction electron's spin can influence nuclear magnetic moment (= knight shift ).
So if we measure some change in the nuclear magnetic resonance, it means spin wave, they insist.
Again, it's impossible to discriminate spin wave and various other effects on nucleus.
But researchers have to write papers even under the condition of "Shut up and calculate !" physics.
In these strict situations, there are only abstract math operators with up or down spin.
You can feel their strong desire to link unreal "spin" to some other detectable things.
Problem is how we link this imaginary susceptibility Im χ to actual experiments.
They approximately express this χ like Eq.42.
(Eq.42)
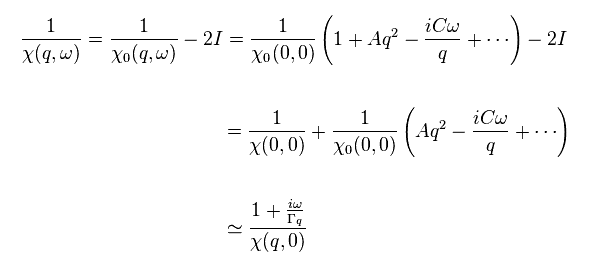
Of course, the form of Eq.42 is completely artificial and speculative.
They just choose the form of Eq.42 to fit neutron scattering experiments.
These A, C and ω cannot be gotten from theory itself.
Here they define
(Eq.43)
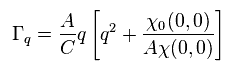
Furthermore, after introducing some new definitions, they make imaginary χ like Eq.44.
(Eq.44)
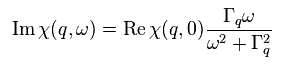
Im χ and Re χ are "imaginary" and "real" parts of χ
Spin wave themselves cannot be confirmed directly, so the relation of Eq.44 is only speculation.

2013/12/26 updated. Feel free to link to this site.