Top page (correct Bohr model including the two-electron atoms).
Electron spin is an illusion !
Our new Bohr model has succeeded in calculating the Helium ionization energy more correctly than the quantum mechanical variational methods as shown in the Top page.
In this new successful Bohr model, the two electrons of the helium atom (He) are moving on the orbits of just one de Broglie's wavelength which are perpendicular to each other.
This model can explain the phenomena of Pauli exclusion principle correctly, because there is no space for the third electron to enter this new two-electron Bohr atom.
Surprisingly, this new atomic structure of the Bohr's helium can be applied to other two-electron atoms (ions ), Lithium ion (Li+), Beryllium (Be2+), Boron (B3+) and Carbon (C4+) ions, too.
(See this page.)
Furthermore, the ionization (ground state) energy of the three-electron atom lithium (Li) can be calculated correctly using the approximate "2S" Bohr orbit. (See this page.)
We have succeeded in visualizing the six electrons' orbits in oxygen atom (O) as shown in oxygen page.
(If you have already read this oxygen page, please proceed to the next section, All orbits come to be stable in the equilibrium state ? .)
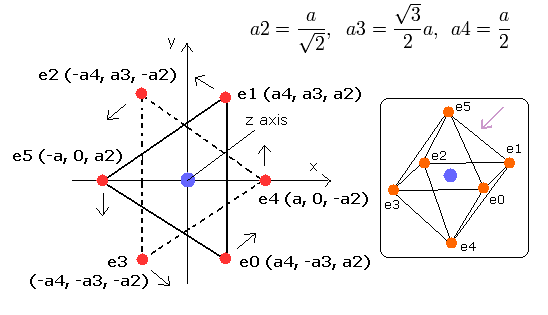
Here six outer shell (valence) electrons of oxygen atom are arranged octahedrally
The neutral oxygen has eight electrons, in which two 1S electrons are very close to the nucleus.
So approximately we suppose these six electrons are moving around one +6e central nucleus (+8e-2e = +6e).
And six outer shell electrons are thought to be avoiding each other and moving symmetrically around this nucleus.
In the regular polyhedrons, the octahedron has six vertices (= six outer shell electrons ), so we can suppose the six outer shell electrons of oxygen are arranged like octahedron as shown in Fig.1.
Fig. 1. Estimated Oxygen atom. (Octahedron). Nucleus=(0,0,0)

Here, we try to visualize the electron's motion of oxygen atom on the screen using the next sample JAVA program (version 1.5 (or 5.0)).
Sample JAVA program (O visualization)
This program is a little long. So if you copy and paste the above program source code into some text editor,
you can easily compile and run this.
In this program, class file name is oxygen2, so save this text editor as "oxygen2.java", and compile it.
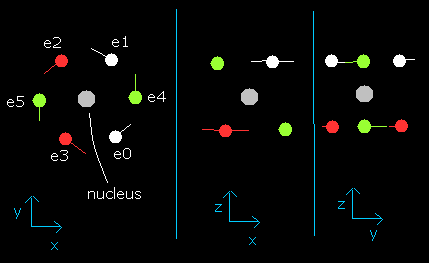
In this program, the oxygen nucleus is shown as a gray circle. (See Fig.2.)
Six electrons are white (e0, e1), red (e2, e3), and green (e4, e5) circles.
The x, y and z axes are the same as Fig. 1.
The left, center and right figures are x-y, x-z, and y-z planes, respectively.
And the velocity vector of each eletron is shown as a line.
Fig. 2. O nucleus and six valence electrons in the program (wn=0)
Each coordinate of electrons (+X (MM), +Y (MM), +Z (MM)) in the text box means "relative" position from the nucleus.
Here we use the new units, as follows.
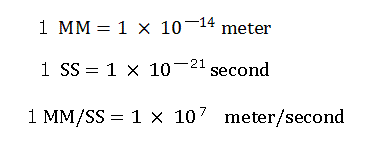
"nuc (MM)" means the distance between the nucleus and each electron.
"VX: VY: VZ" means the ratio of each component of the initial electron's velocity vector.
So, (VX: VY; VZ)=(100:100:0) is the same as (VX: VY: VZ)=(10:10:0).
When you choose the number (=wn) of de Broglie's waves (0.1 -- 2.0) in the scrollbar, and put "orbit" button, this program starts to compute the electron's orbit until de Broglie's waves contained in the orbit becomes wn.
About the detailed method, see Top page.
At short time intervals (1 SS), we calculate the Coulomb forces among electrons and nuclei, and change each velocity vector based on that result.
And we also compute the number of de Broglie's waves contained in the short segments at each electron.
(In this program, the total energy of the six valence electrons are supposed to be -433.103 eV = sum of 1-6 ionization energy.)
And this program outpus the last coordinate and velocity vector of each electron in both the text box and image area.
When you type the value (=a (MM) of Fig.1) in the textbox next to "radiu" button and click this button, the size (radius) of the six electrons' octahedron changes as shown in Fig.1.
First, we input the value "3820" as a (MM), and click "radiu" button.
(In this case, the value a of Fig.1. becomes 3820 (MM), and the first distance (=nuc) between nucleus and each electron becomes 4678 MM.)
And when we choose the value "0.5" in the scrollbar as the number of de Broglie's waves (wn), and click "orbit" button, the calculation starts and the image result becomes as follows,
Fig. 3. Oxygen electrons at wn = 0.5
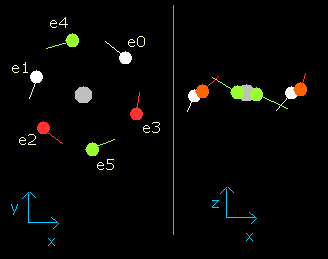
When the electrons have moved their orbits of 0.5 de Broglie's wavelength (wn=0.5), all six valence electrons of oxygen are arranged near the x-y plane (Fig. 3, right panel).
And at this point (wn=0.5), the distance between nucleus and electron is about 4204 MM.
Next, click the "retur" button, which go back to the initial condition (wn=0).
And choose the value "0.9" in the scrollbar as the number of de Broglie's waves (wn), and click "orbit" button again. (Fig.4)
Fig. 4. Oxygen electrons at wn = 0.9
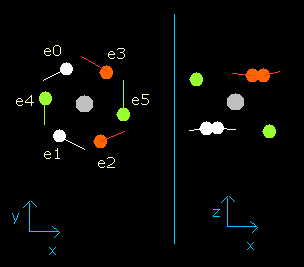
This result shows that when the electrons have moved their orbits of 0.9 (about 1.0) de Broglie's wavelength (wn=0.9), all six valence electrons of oxygen are on the opposite side from their initial positions.
At this point (wn=0.9), the distance between mucleus and electron becomes the shortest. ( = 3801 MM).
Click the "retur" button again, choose the value "1.9", and click "orbit" button.
The result is, (Fig. 5)
Fig. 5. Oxygen electrons at wn = 1.9 (=almost same as wn=0.0)
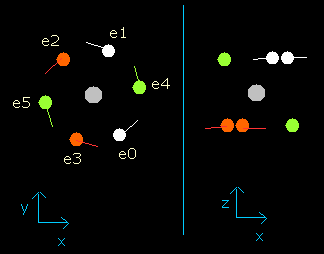
So this result proves that the all six electrons go back to almost original position when the the number of de Broglie's waves contained in their orbits becomes 1.9 (almost 2.0).
(Probably, these orbits are precessing or swaying a little.)
If you set a=3100 MM, which means the initial distance between the nucleus and electrons is 3796 MM, this distance (nuc) becomes the longest at wn=0.9 (4677 MM).
Try this, too.
In the above program. we suppose the "central positive charge" is just +6.0e (= +8e (nucleus) -2e (two 1s electrons) = +6e)
But as shown in this this oxygen page, the two 1S electrons are about 700 MM apart from +8e oxygen nucleus. (They don't stick to the nucleus.)
So, the "effective" positive charge which influences the six valence electrons are probably a little bigger than +6.0e.
Here, we try this orbital calculation again, supposing this central positive charge is +6.3e instead of +6.0e
Sample JAVA program. (central charge +6.3e instead of +6.0e)
This sample program is almost same as the above sample program except for the central positive charge (+6.0e --> +6.3e).
In this program, when the orbital length becomes just 2.0 de Broglie's wavelength, all six valence electrons of oxygen can return to their original positions, as follows,
Fig. 5-2. Oxygen electrons at wn = 0.0 and wn = 2.0 ("effective" charge = +6.3e)
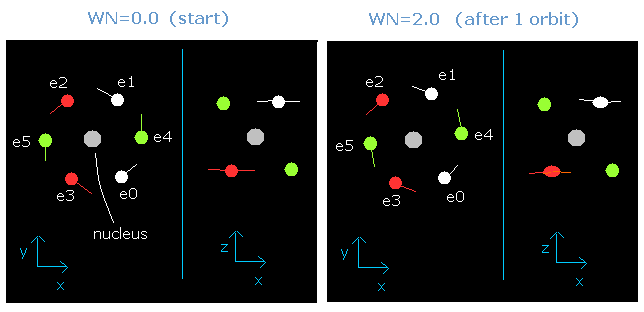
This result is very important.
When the total energy of the six valence electrons is determined (=-433.103 eV), the average length (or radius) of one-round orbit is fixed.
(This means that if the total energy of electrons is determined, the average length and the number of de Broglie's waves contained in the one-round of the orbit is fixed "automatically".)
And this number proves to be 2.0 in the case of neutral oxygen atom.
(So this result shows that the six valence electrons of oxygen atom are moving on the orbits of 2.0 de Broglie's wavelength.)
When the central positive charge (Z) is just +6.0e (=+8e-2e), the number of de Broglie's waves (wn) contained in one orbit is 1.9.
But actually the two 1S electrons don't stick to the +8e nucleus, so if we suppose this charge (Z) is +6.3e (a little bigger than +6.0e), the de Broglie's wave becomes just 2.0, as shown above.
Here we try to prove this using the Virial theorem.
We suppose that the six valence electrons are arranged "octahedrally" around +Ze central charge, as follows,
Fig. 5-3. Oxygen valence electrons ("effective" charge = +Ze)
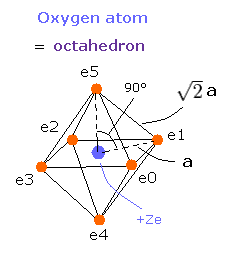
In Fig. 5-3, the distance between an electron and the central positive charge is a.
According to the Virial theorem, "average" total potential (V) and kinetic (T) energies satisfy the relation,
< V > = -2 × < T > , E = V + T
The total energy (E) of the six valence electrons is -433.103 eV, so this potential energy (V) becomes 2 × -433.103 = -866.206 eV.
When we calculate this potential energy (V) using Fig. 5-3 model, this V ( eV --> J ) becomes,
(by calculating the interactions between electron - nucleus and electron-electron,)
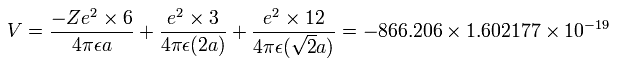
And the total kinetic energy (T) of the six electrons is 433.103 (eV), as follows,
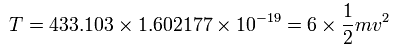
And by calculating the Coulomb forces among the particles of Fig.5-3, the force (F) acting on electron 0 becomes,
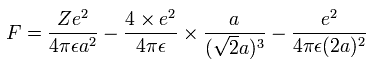
Using the above velocity (v) (of T) and F, we suppose the centrifugal force is equal to the force (F), as follows,
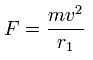
This r1 is "temporary" radius, which appears by this relation.
Using this r1, we can calculate the number of de Broglie's waves (wn) contained in one orbit, as follows,
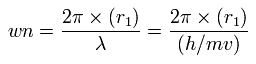
When Z = 6.0, this wn becomes 1.88 (almost 1.9).
And when Z = 6.3, this wn becomes just 2.01.
So we can prove this fact using the Virial theorem.
If you change some values (coordinate or velocity vectror) of electrons a little from the initial ones, and click "orbit" button, the six electrons will scatter unsymmetrically even if their energies are the same.
Does this mean that electron's motion (average orbital radius) becomes unstable even if their energies are the same?
The answer is that electron's orbital radius becomes stable in the equilibrium state.
Here, we explain this using a simple two-electron atom as shown in Fig. 6.
(This is only an "approximate" example. so it is not an actual atom.)
Fig. 6. Orbits come to be "unsymmetrical" with time ?
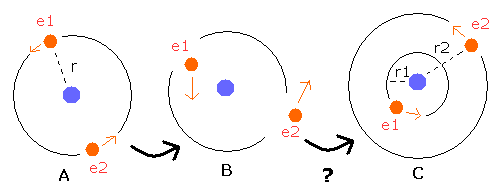
In Fig.6 - A, both the two electrons are moving "symmetrically" on the orbits of the same radius r .
We assume that these two electrons have the same energies (E = V + T ).
If you change the direction of the initial velocity vectors to "unsymmetrical" ones like Fig.6-B, these two electrons come to be moving like Fig.6-C ?
Basically, when the average radius of the orbit is stable, the centrifugal forces are equal to the Coulomb forces, as shown in Eq. 1
(Eq. 1.)
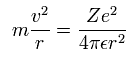
where r is the radius, m is the mass of an electron, v is the electron's velocity, and -e is the electron's charge.
Z is the "effective" positive charge, which include the influences of the nucleus and other electrons.
So the total energy (E) of each electron is the sum of the kinetic and potential energies. (Eq.2)
Substituting Eq.1 into the kinetic energy term of Eq.2, the result becomes,
(Eq. 2.)
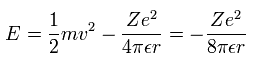
If electron 1 (e1) is moving on the orbit which radius (r1) is smaller than the original r (r1 < r), electron 2 (e2)
come to be moving on the orbit which radius (r2) is longer than the original r (r2 > r), because the sum of these two electrons' energies doesn't change. (Fig.6-C)
So, from the viewpoint of electron 1 (e1), the "effective" positive charge Z becomes bigger, because it enters the inner orbit than the electron 2 .
According to Eq.2, if the r is smaller and Z is bigger, total energy of electron 1 is smaller than the original one.
(On the other hand, the total energy of the electron 2 becomes bigger than the original one.)
This result is inconsistent with the first assumption that the two electrons have the same energies.
As a result, when the energy of each electron is the same, all electrons come to be moving stably on the "symmetrical" orbits with time.
Next let's try the visualization of Water(H2O).
In the water molecule, the dissociation energy required to perform the reaction (H2O --> 2H + O ) is 9.6066 eV (926.9 kJ/mol).
So the average single O-H bond energy of the water is 9.6066/2 = 4.8033 eV.
This bond energy is not very large, so it can be thought that each electron of the hydrogen and oxygen atoms keeps bound to the original nuclei.
The total energy of H2O is -433.103 (O) - 2 × 13.606 (H) - 9.6066 (bond energy) = -469.92 eV.
Fig. 7. Water (H2O) molecule model
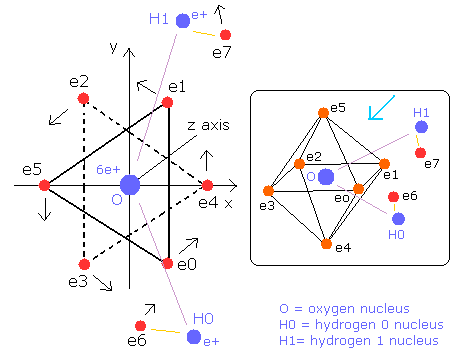
The O-H bond length of H2O is 9584 MM (= 0.9584 × 10-10 meter).
The H-O-H angle is 104.45 degrees, which is a little larger than 90 degrees (e0 - nucleus - e1 angle of oxygen).
So the H-H length is 15150 MM (= 1.5150 × 10-10 meter).
Here we compute the electron's orbit of water using the next sample JAVA program.
Sample JAVA program (H2O visualization)
The structure of the water molecule is unsymmetrical, which is different from oxygen and methane (CH4).
So, it is much more difficult to find the proper electron's orbit (=equilibrium state) of water.
There are two reasons of this difficulty as follows,
If we set the initial condition, which is a little different from the proper one (= equilibrium state), octahedral symmetrical structure is easily broken before electron has moved one round of its orbit.
Of course, due to the existence of two hydrogen atoms, we can't use the same symmetrical initial condition as the oxygen atom. (If you try this, you would know.)
So it is very hard to find the correct initial condition (=coordinate and velocity vector).
Second, it is possible that six valence electrons don't have the same energies, because the distances between hydrogen nucleus and electrons are different.
So we need to know how the bond energy (=9.6066 eV) of H2O is distributed to each electron.
Acoording to the Virial theorem, in the equilibrium state, the average potential energy (V) and kinetic energy (T) satisfy the relation, -1/2 V = T
In the case of hydrogen and oxygen atom, it is easy to calculate V, because there is only one nucleus in them.
But in the case of water (H2O), it is a little complicated, because V needs to include the repulsive potential energy between nuclei.
The problem is how this repulsive potential energy between nuclei should be distributed to each electron.
In this program, we compute the potential energy of each electron from the initial coordinate.
To form the O-H bond of water, two positive nuclei needs to be attracted by electrons which belong to another nucleus. (Fig. 8)
Fig. 8. O-H bond and the change of each potential energy
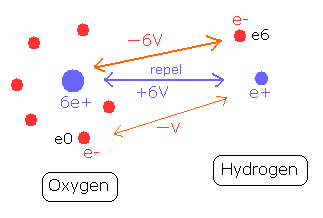
The hydrogen nucleus (e+) is attracted by the six electrons of the oxygen atom.
The potential energy between the hydrogen nucleus and one electron (e0) of oxygen is -V.
On the other hand, the oxygen nucleus is attracted only by one electron (e6) of hydrogen atom, so the potential energy between the oxygen nucleus and the hydrogen electron (e6) is - 6V, which bond is six times stronger than the above case.
So the potential energy of the hydrogen electron (e6) becomes -6V lower by O-H bond, but instead, e6 does much work to bind two repulsive positive nuclei, which makes the e6 potential energy higher than this.
Considering this fact, in this program, after calculating potential energies between electron-electoron and electron-nucleus, the potential energies between repulsive positive nuclei are distributed to each electron.
For example, when this repulsive potential energy is +6V, the distribution ratio is 6:1 in e6 and e0. (= -6V: -V )
As the oxygen has six e0-e5 electrons, +6V × 6/(1x6 +6) = +6V / 2 is distributed to e6, and +6V × 1/(1x6+6)= +6V / 12 is distributed to e0.
And then, based on each electron's potential energy, the kinetic energy is distributed to each electron.
But this method applies only to "average" state.
So we need to adjust these values a little.
Like the oxygen program, choose the de Broglie's wave's number in the scrollbar and click "orbit" button in this H2O program.
First, choose as small value as possible (for example, 0.3 and 0.5 instead of 1.9 and 2.0).
After calculating the electron's orbit, if one electron (for example, e0) of oxygen atom come closer to nucleus than other five electrons, we change the direction of initial velocity vector of e0 outward a little, or transfer other electron's kinetic energy to e0 a little (0.01 - 0.1 eV).
To transfer the initial kinetic energy between electrons, choose electron's numbers (el0 - el7) in the two scrollbars of the last row,
type the transferring values (eV) (for example, 0.1, 0.01, 0.2... and so on) in the textbox next to them, and press the Enter key.
When you run this program, the adjusted initilal values are automatically set in the textboxes.
So you just choose de Broglie's wave number (wn) in the scrollber, and click "orbit" button.
When wn is 0.0 (nuc of e0 is 4589 MM), the electron's state is,
Fig. 9. Water (H2O) electrons in the program (wn=0.0)
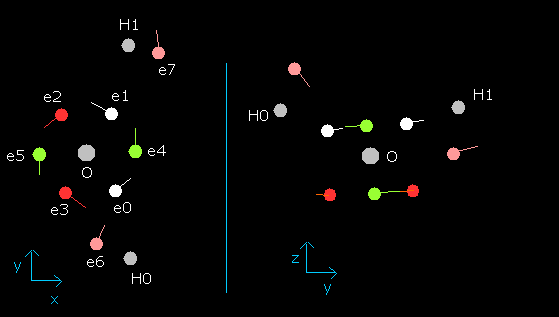
When wn is 0.5, e0-e5 electrons of water are almost on the x-y plane, as follows,
Fig. 10. Water (H2O) electrons at wn=0.5
In this state (wn=0.5), nuc of e0 becomes 4266 MM.
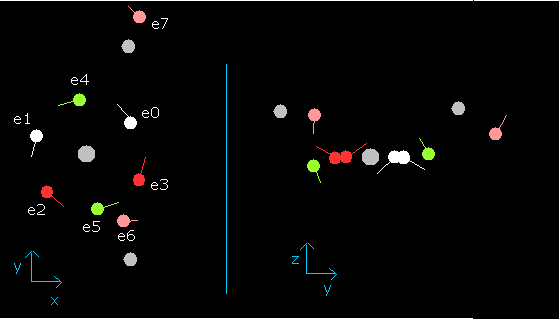
When wn is 0.9, each electron's position becomes,
Fig. 11. Water (H2O) electrons at wn=0.9
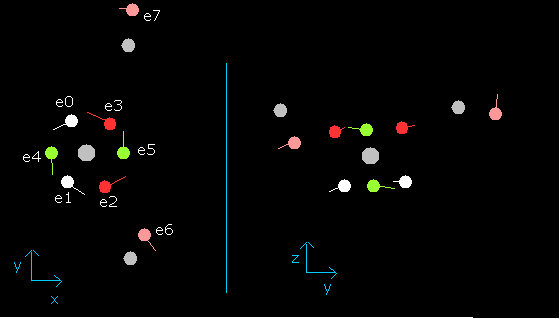
In this state (wn=0.9), six valence electrons of oxygen are on the opposite side from their initial positions.
And nuc = 3949 MM is the shortest length.
When wn is 1.9, each electron's position becomes,
Fig. 12. Water (H2O) electrons at wn=1.9 ( = almost same as wn=0.0)
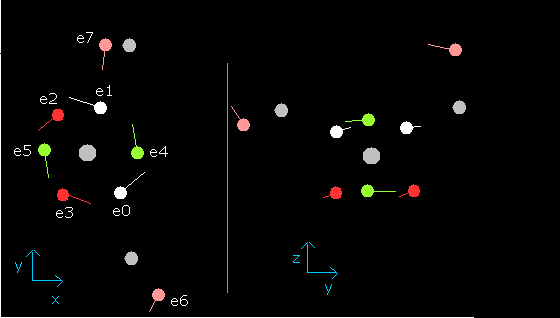
This result shows that orbital length of water's oxygen is almost 2.0 de Broglie's wavelength.
(In case of wn=2.0, electrons precesses a little. Or, as shown in the above oxygen case, probably it's better to change the central positive charge into +6.3e (a little bigger than +6.0e).)
See also this page (Virial theorem of H2O).
The last distance between electron 0 and nucleus is 4588 MM, which is almost same as 4589 MM ( wn=0.0 ).
This program also shows the result of de Broglie's waves of hydrogen's electron 6 on the command prompt window.
The important thing is that the velocity of oxygen's electrons (e0-e5) are faster than hydrogen's electron (e6,e7).
So, when the electron 0 has moved its orbit of 2.0 de Broglie's wavelength, the electron 6 moves about 0.6 de Broglie's wavelength.
Slow electron 6 can not move one round of its orbit during this time.
The orbital periods are different in them.
(Caution: the orbital length of hydrogen's electron is 1.0 de Broglie's wavelength.)
In the first condition, the potential (V) and kinetic (T) energies of each electron satisfy the relation -1/2 V > T as shown in the textboxes.
So this state is equivalent to that on the long axis side of the "elliptical" orbit.
(Actually, nuc=4589 MM of wn=0.0 is longer than nuc=3949 MM of wn=0.9.)
And in the last row of the textboxes, (FX, FY, FX) shows the each component of the force acting on the oxygen nucleus.
Here, we use the hydrogen atom of Bohr radius as the standad values expressing force.
The force between an electron and a nucleus of the hydrogen atom is defined as 1000.
So the result of (FX,FY,FZ) =(-71, 98, -145) means that the water's oxygen nucleus is almost in the equilibrium state. (= the force acting on the oxygen nucleus is almost zero.)
In the methane (CH4) molecule, which is a tetrahedral structure, the carbon atom can bind to four hydrogen atoms.
But as show in water (H2O) molecule, the oxygen atom can bind to only two hydrogen atoms.
But the sulfur atom (S), which has also six valence electrons like oxygen, can bind to more than two atoms.
For example, H2SO4 (sulfuric acid)....
Fig. 13. Oxygen-like and Carbon-like atoms
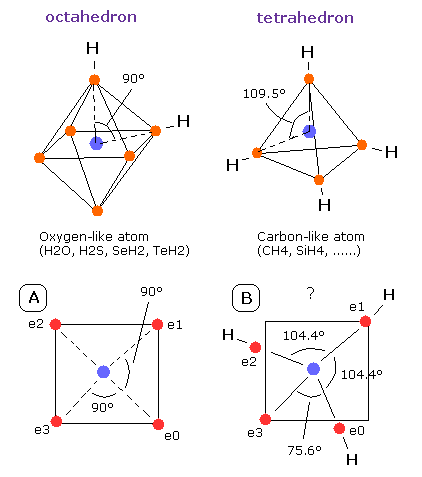
What is the difference between sulfur (S) and oxygen (O) atoms ?
As shown in Fig.13, the oxygen atom is more crowded than the carbon atoms, so the angle of oxygen (=90 degrees) is smaller than carbon (=109.5 degrees).
This indicates that the oxygen atom doesn't have much room to bind to other atoms.
But in the sulfur, the six valence electrons belong to the larger orbit of 3 de Broglie's wavelength, so the interaction between hydrogen atoms is much weaker than the oxygen.
Actually, the angle H-S-H of hydrogen sulfide is 92.1 degrees (almost 90 degrees), which means the "octahedral structure" is almost kept in H2S.
But the angle H-O-H of water is 104.45 degrees, so "octahedral" structure is a little broken in water.
The important point is that the angle 104.45 degrees is between 90 (O) and 109.5 (C) degrees as shown in Fig.13.
And if a third hydrogen atom binds to the H2O, this "octahedral" structure would be further broken (See Fig.13-B).
In this case, the angle of e0-nucleus-e3 becomes "unnaturally" as small as 75.6 degrees.
So, in the H2O, it is thought that to keep "octahedral" structure, more than two hydrogen atoms can not bind to the oxygen.

2010/10/6 updated. Feel free to link to this site.