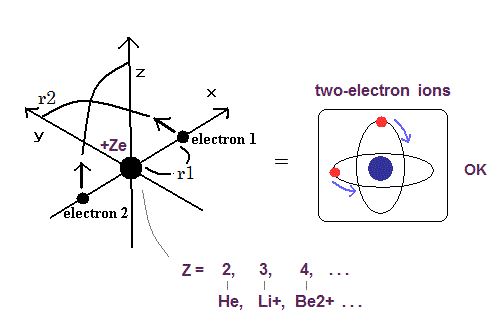
Top page (correct Bohr model including the two-electron atoms).
Electron spin is an illusion !
Our new Bohr model has succeeded in calculating the Helium ionization energy more correctly than the quantum mechanical variational methods as shown in the Top page.
In this new successful Bohr model, the two electrons of the helium atom (He) are moving on the orbits of just one de Broglie's wavelength which are perpendicular to each other.
This model can explain the phenomena of Pauli exclusion principle correctly, because there is no space for the third electron to enter this new two-electron Bohr atom.
Surprisingly, this new atomic structure of the Bohr's helium can be applied to other two-electron atoms (ions ), Lithium ion (Li+), Beryllium (Be2+), Boron (B3+) and Carbon (C4+) ions, too.
(See this page.)
Furthermore, the ionization (ground state) energy of the three-electron atom lithium (Li) can be calculated correctly using the approximate "2S" Bohr orbit.
(Fig.1) Two-electron Atomic Model ( He, Li+, Be2+, B3+, C4+ .. O6+.. Ne8+. )

Here we show the ionization energies of neon.
| Name | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th | 10th |
|---|---|---|---|---|---|---|---|---|---|---|
| Neon (Ne) | 21.56 | 40.96 | 63.45 | 97.12 | 126.21 | 157.93 | 207.27 | 239.09 | 1195.83 | 1362.20 |
As shown in this Table 1, the ionization energies of 1S electrons (red values) are much bigger than other ionization energies.
This means that also in neon, only two "1S" electrons are much closer to the nucleus than other electrons.
The sum of the ionization energies of neon ion ( Ne8+ ) is 1195.83 + 1362.20= 2558.03 eV
(See the above Table 1. So the experimental value of the total (ground state) energy is -2558.03 eV )
We suppose the two electrons of Ne8+ are orbiting like Fig. 1.
See the Top page (He) or Li+ page about the detailed computing methods.
Here we use the following sample programs.
(In this program, we use the new units, 1 MM = 10-14 meter, 1 SS = 10-23 second, 1 MM/SS = 109 m/s. )
JAVA program to compute two-electron atoms.
Simple C language program.
In the upper program, input the Neon atomic number Z = 10 after running it.
Table 2 shows the results of r1 and WN (= number of de Broglie's waves contained in one quarter of the orbit ) in which last VY ( y component of electron 1's velocity after moving one quarter of its orbit ) is zero at various energy levels of Ne8+.
( When the last VY is zero, the electrons move on the stable orbits. )
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -2550.0 | 547.0 | 0.25064 | 1.00254 |
| -2555.0 | 546.0 | 0.25040 | 1.00158 |
| -2560.0 | 545.0 | 0.25015 | 1.00058 |
| -2563.0 | 544.5 | 0.25000 | 1.00000 |
| -2570.0 | 543.0 | 0.24966 | 0.99865 |
| -2575.0 | 541.8 | 0.24942 | 0.99767 |
| -2580.0 | 540.8 | 0.24918 | 0.99671 |
So when the total energy of Ne8+ is -2563.0 eV, the number of de Broglie's waves contained in one orbits becomes just 1.00000.
As I said above, the experimental value of the Ne8+ energy is -2558.03 eV.
The error is only 5.00 eV. The ionization energy of Ne8+ is very big, so the error is only 0.19%.
( This little difference is thought to be caused by Ne8+ big positive charges attracting some negative charges around it. )
So it can be said that also in the neon ion (Ne8+), the orbital planes of the two electrons are almost perpendicular to each other.
To confirm the third electron of neon enters the orbit of two (not one) de Broglie's wavelength, we try computing the energy of the three-electron neon ion (Ne7+).
Neon ion (Ne7+) has two electrons in 1S orbital, and one electron in 2S orbital.
The two electrons of 1S state are attracted to the 10e+ nucleus strongly, so they are much closer to the nucleus than the 2S electron.
So approximately, we can suppose the 2S electron is moving around the 8e+ nucleus ( +10e - 2e = +8e ) on the circular orbit of the two de Broglie's wavelength.
(This means that we can use the equations of the hydrogen-like atoms in 2S electron approximately.)
According to the Bohr hydrogen-like model, the radius (Rb) of the n × de Broglie's wavelength orbit is,
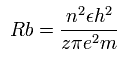
(when z = 1 and n = 1, Rb becomes "Bohr radius".)
In the 2S electron of Ne7+, the positive charge of the nucleus (z) is supposed to be 8+ (see above), and n is 2.
So this Rb is 4/8 × Bohr radius ( = 0.2645 × 10-10 meter = 2645 MM ) .
(Here we use the new units, 1 MM = 10-14 meter, 1 SS = 10-23 second, 1 MM/SS = 109 m/s )
The energy levels of the hydrogen-like atom is known to be,
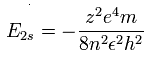
In the 2S electron of Ne7+, we substitute n=2 and z=8 into this equation.
So we suppose the neon ion (Ne7+) model as follows,
(Fig.2) Neon ion (Ne7+) model
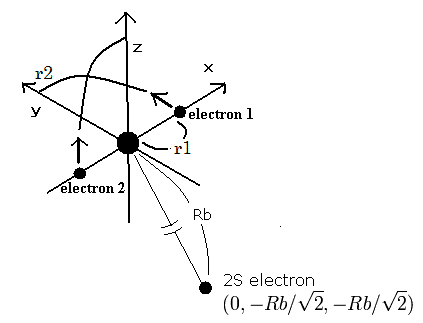
The two electrons of 1S state are avoiding 2S electron, so we fix the 2S electron at ( 0, - Rb / √2, - Rb / √2 ) as shown in Fig. 2.
(Fig. 2. shows the relative positions, But actually, this 2S electron is rotating around the nucleus slower than the 1S electrons.)
Like Ne8+ (see also top page ), when the electron 1 is at (x, y, 0), the electron 2 is at ( -x, 0, y ).
So the distances among the particles are,
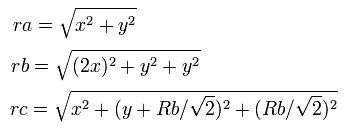
where ra is the distance between the electron 1 and the nucleus, rb is between the two 1S electrons, and rc is between the electron 1 and 2S electron, respectively.
The x component of the acceleration (m/sec2) of the electron 1 is,
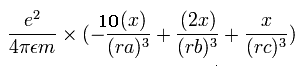
In the same way, the y component of the acceleration (m/sec2) of the electron 1 is,
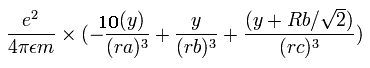
Then we compute the number of de Broglie's waves contained in one quarter of the 1S orbit like Ne8+
JAVA program ( three-electron atoms ).
Simple C language program.
In this program, we first input Neon atomic number Z = 10.
Table. 3 shows the results in which the last VY ( y component of electron 1's velocity after moving one quarter of its orbit ) is the closest to zero in Ne7+.
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -2780.0 | 548.0 | 0.25055 | 1.00219 |
| -2785.0 | 547.0 | 0.25030 | 1.00120 |
| -2790.0 | 546.0 | 0.25059 | 1.00024 |
| -2791.17 | 545.7 | 0.25000 | 1.00000 |
| -2800.0 | 544.0 | 0.24957 | 0.99828 |
| -2805.0 | 543.0 | 0.24933 | 0.99731 |
| -2810.0 | 542.0 | 0.24908 | 0.99624 |
This results shows that when the ground state energy of Ne7+ ion is -2791.17 eV, the orbital length becomes just 1.00000 × de Broglie's wavelength.
The experimental value of the ground state energy of the neon (Ne7+) ion is = -239.09 -1195.83-1362.20 = -2797.12 eV.
So the calculation error is only 5.97 eV ( 0.21 % ).
(This small error is probably caused by using the "approximate" orbit of the 2S electron.)
This means that it is almost correct to say that the three electrons of the neon ion (Ne7+) are moving like Fig.2.
(The third electron of neon enters the orbit of 2 ( not 1 ) × de Broglie's wavelength.)
In the neutral neon (Ne), how are eight outer shell (valence) electrons moving ?
The neutral neon has ten electrons, in which two 1S electrons are very close to the nucleus (see above Ne8+ section).
So "approximately" these eight electrons are moving around one +8e central nucleus (+10e-2e = +8e).
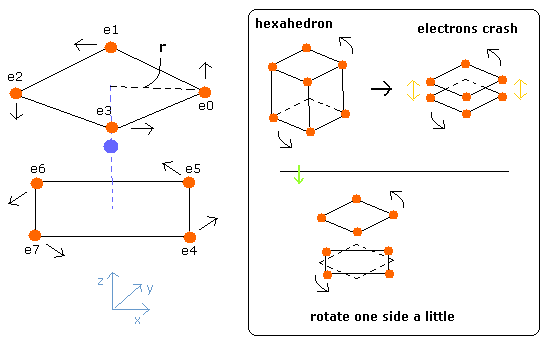
(Fig.3) Neutral Neon model
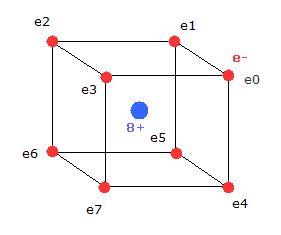
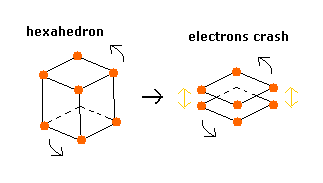
Considering the repulsive Coulomb forces among eight valence electrons ( e0 - e7 ), these outer electrons are distributed like regular hexahedron.
In this hexahedron configuration, the outer 8 electrons are most stable.
But different from other atoms such as carbon, in Fig.3 model, the outer electrons of upper and lower crash into each other, while they are orbiting around the nucleus.
(Fig.4) Upper and lower electrons' crash.
As shown in top page, mysterious Pauli exclusion principle is caused by two 1s orbits, which are perpendicular to each other.
So also in noble gases such as Neon, this de Broglie wave's nature is naturally related.
To avoid this crash, using helium perpendicular de Broglie waves, the eight outer electrons' orbits are thought to be
(Fig.5) Neutral Neon's eight orbits of valence electrons.
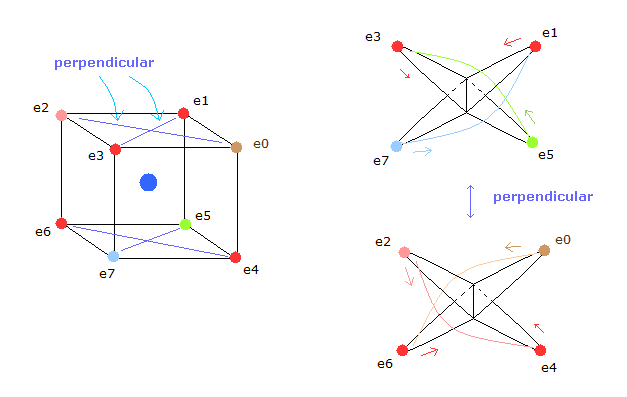
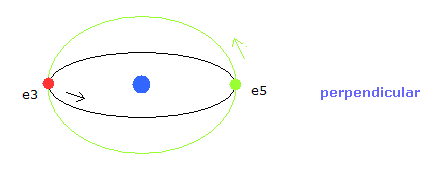
In Fig.5, for example, the orbits of the electron 3 and 5 ( e3 and e5 ) have two common vertices, and perpendicular to each other, like
(Fig.6) Orbits perpendicular to each other.
In Fig.5 model, the eight valence electrons don't crash into each other.
And the eight valence electrons don't need to be in a single common plane like Fig.8 ( so Fig.8 model needs to be a little corrected ), when they are passing each other.
And each two electrons having two common vertices are perperndicular to each other like helium model of top page.
( Pairs are e1-e7, e3-e5, e2-e4, e0-e6. )
So the eight outer electrons have their own different orbits.
Considering the symmetric structure of polyhedron, and de Broglie wave's destructive interference, this eight outer electrons is the limit of n = 2 (= two de Broglie wavelength ) energy levels.
( Different from n = 1, the orbit can be elliptical due to radial de Broglie wave. )
Here we confirm the eight valence electrons of Neon is moving around on 2 times de Broglie wavelength orbit considering only Coulomb interaction.
So this simple model is not true, but we can get some images.
Actually, the two 1S electrons are a little apart from the +10e nucleus.
As a result, the "effective" central positive charge becomes a little bigger than +8e .
How much is this "effective" central positive charge
As shown in upper Ne7+ ion section, the energy levels of the hydrogen-like atom is,
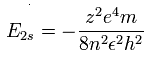
If the two 1S electrons of Ne7+ stick to +10e nucleus completely, we should substitute n=2 and z=8 into this equation.
So the total energy (E) becomes -13.606 (H) × 64/4 = - 217.696 eV.
But the 8th ionization energy of Ne (Table 1) is 239.09 eV.
So when we use this -239.09 eV instead of -217.696 eV in the upper energy equation, z becomes +8.384, which is a little bigger than +8
As the valence electrons increase, the energy change becomes smaller when we consider the 1S electrons are apart from the nucleus.
But on the other hand, as the valence electrons increase, the ionization energies become smaller, too.
So as a result, it is thought that the ratio of 8.384 to 8 doesn't change in other valence electrons.
And here we suppose the total energy of the eight valence electrons of the neon is -953.6126 eV (= the sum of 1-8th ionization energies).
Here, we try to visualize the eight valence elecrons' motion using the next sample JAVA program.
Sample JAVA program (Ne) (central charge = +8.4e)
The eight outer shell electrons are thought to be avoiding each other and moving symmetrically around this nucleus.
In the regular polyhedrons, the hexahedron has eight vertices (= eight outer shell electrons ).
But if we suppose the eight outer shell electrons of neon are arranged like hexahedron, electrons crash into each other while rotating as shown in Fig. 3.
So considering all scenes of their motions, we rotate one side of the hexahedron by 45 degrees (Fig. 7).
(Fig.7) Estimated electron's motion of Neon ( only Coulomb interaction )
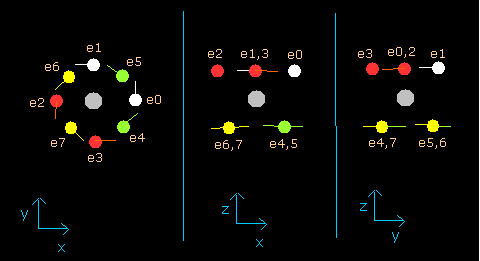
In this program, the neon nucleus is shown as a gray circle. (See Fig.8.)
Eight electrons are white (e0,1), red (e2,3), green (e4,5), and yellow (e6,7) circles.
The x, y and z axes are the same as Fig. 3.
The left, center and right figures are x-y, x-z, and y-z planes, respectively.
And the velocity vector of each eletron is shown as a line.
(Fig.8) Ne nucleus and eight valence electrons in the program (wn=0.0)
Each coordinate of electrons (+X (MM), +Y (MM), +Z (MM)) in the text box means "relative" position from the nucleus.
Here we use the new units, as follows.
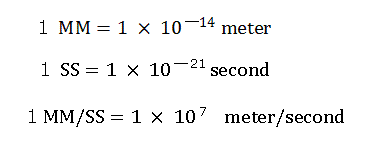
"nuc (MM)" means the distance between the nucleus and each electron.
"VX: VY: VZ" means the ratio of each component of the initial electron's velocity vector.
So, (VX: VY; VZ)=(100:100:0) is the same as (VX: VY: VZ)=(10:10:0).
When you choose the number (=wn) of de Broglie's waves (0.1 -- 2.0) in the scrollbar, and put "orbit" button, this program starts to compute the electron's orbit until de Broglie's waves contained in the orbit becomes wn.
About the detailed method, see Top page.
At short time intervals (1 SS), we calculate the Coulomb forces among electrons and nuclei, and change each velocity vector based on that result.
And we also compute the number of de Broglie's waves contained in the short segments at each electron.
(In this program, the total energy of the eight valence electrons are supposed to be - 953.6126 eV = sum of 1-8 ionization energy.)
And this program outpus the last coordinate and velocity vector of each electron in both the textboxes and image area.
When you type the value (=r (MM) of Fig.7) in the textbox next to "radius" button and click this button, the size (radius) of the neon changes as shown in Fig.3.
First, we input the value "2925" as r (MM), and click "radius" button.
(In this case, the value r of Fig.7. becomes 2925 (MM), and the first distance (=nuc) between nucleus and each electron becomes 3582.37 MM.)
And when we choose the value "0.5" in the scrollbar as the number of de Broglie's waves (wn), and click "orbit" button, the calculation starts and the image result becomes as follows,
(Fig.9) Neon electrons at wn = 0.5
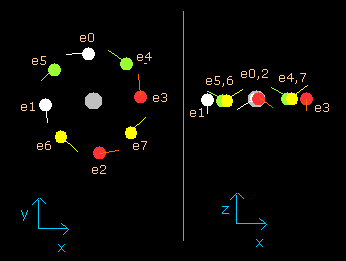
When the electrons have moved their orbits of 0.5 de Broglie's wavelength (wn=0.5), all eight valence electrons of neon are arranged near the x-y plane (Fig.9, right panel).
And at this point (wn=0.5), the distance between nucleus and electron is about 3555.09 MM.
The distance between adjoining electrons are (2 π × 3555.09) / 8 = 2790.74 MM.
As shown in Top page, the radius of new Bohr's helium atom is about 3000 MM.
So at this distance, it is thought that de Broglie's waves are interacted and entangled with each other.
Next, click the "return" button, which go back to the initial condition (wn=0).
And choose the value "1.0" in the scrollbar as the number of de Broglie's waves (wn), and click "orbit" button again. (Fig.10)
(Fig.10) Neon electrons at wn = 1.0
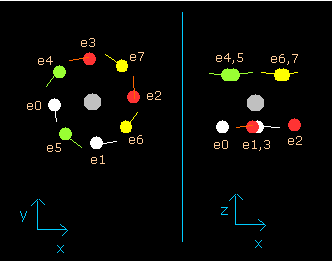
This result shows that when the electrons have moved their orbits of 1.0 de Broglie's wavelength (wn=1.0), all eight valence electrons of neon are on the opposite sides from their initial positions.
At this point (wn=1.0), the distance between nucleus and electron becomes 3379.18 MM.
Click the "return" button again, choose the value "2.0", and click "orbit" button.
The result is, (Fig.11)
(Fig.11) Neon electrons at wn = 2.0 (almost same as wn=0.0)
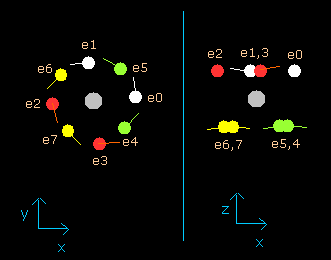
As shown in (Fig.11), all eight valence electrons of neon can go back to their original positions when they move the orbits of 2.0 de Broglie's wavelength.
This result is very important.
When the total energy of the eight valence electrons is determined (=-953.6126 eV), the average length (or radius) of one-round orbit is fixed.
(This means that if the total energy of electrons is determined, the average length and the number of de Broglie's waves contained in the one-round of the orbit is fixed "automatically".)
And this number proves to be 2.0 in the case of neutral neon atom.
(So this result shows that the eight valence electrons of neon are moving on the orbits of 2.0 de Broglie's wavelength.)
In the above Ne7+ ion, we use the +8.0e central charge, because at the starting point of Fig.2, the error by this approximate methods is very small.
See also this page (the relation between inner 1S and 2S electrons).
As shown in the upper sections (Ne8+ and Ne7+), the two 1S electrons are about 540 MM apart from the neon nucleus.
And the shortest distance between the neon nucleus and the eight valence electrons is about 3300 MM according to the upper result.
This means that these eight valence electrons of the neon can be moving around safely, not colliding with the inner 1S electrons.
Next we try to prove this using the Virial theorem.
We suppose that the eight valence electrons are arranged "hexahedrally" around +Ze central charge, as follows,
(Fig.12) Neon valence electrons ("effective" charge = +Ze)
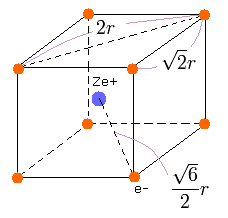
According to the Virial theorem, "average" total potential (V) and kinetic (T) energies satisfy the relation,
< V > = -2 × < T > , E = V + T
The total energy (E) of the eight valence electrons is -953.6126 eV, so this potential energy (V) becomes 2 × -953.6126 = -1907.2252 eV.
When we calculate this potential energy (V) using Fig.12 model, this V ( eV --> J ) becomes,
(by calculating the interactions between electron - nucleus and electron-electron,)
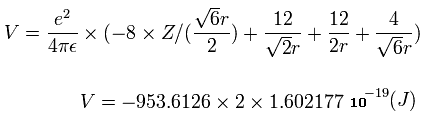
From this equation, we can find the value "r" when Z is determined.
And the total kinetic energy (T) of the eight electrons is 953.6126 (eV), as follows,
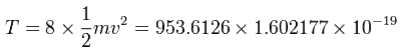
And by calculating the Coulomb forces among the particles of Fig.12, the force (F) acting on an electron (toward nucleus) becomes,
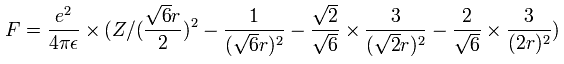
Using the above velocity (v) (of T) and F, we suppose the centrifugal force is equal to the force (F), as follows,
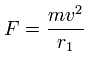
This r1 is "temporary" radius, which appears by this relation.
Using this r1, we can calculate the number of de Broglie's waves (wn) contained in one orbit, as follows,
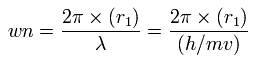
When Z = +8.4, this wn becomes 2.004 (almost 2.0).
So we can prove this fact using the Virial theorem.
It is thought that number eight is the upper limit of valence electrons in 2 × de Broglie's wavelength orbits.
The next regular polyhedron is "icosahedron" which has 12 vertices. (In case of "dodecahedron", 20 vertices).
So, probably it is almost impossible that in these "complicated" polyhedrons all valence electrons are moving stably.
And if the valence electrons increases more than 8, the distance between adjoining electrons of Fig.9 becomes shorter than 2790.74 MM.
It is possible that there is no more de Broglie's wave space in which all electrons can be moving stably in Fig.5.

2010/12/17 updated. Feel free to link to this site.