
トップページ (ヘリウムも含む正確な新ボーア模型)
電子スピンは数学上の産物。
特殊相対論は間違っている。
量子コンピューターは永遠に実現しない。
量子コンピューター?

あなたがたは 量子力学の重ね合わせに基づく 量子コンピューターは 従来のコンピューターに比べて 各段に速く計算する能力があると しばしば聞いたことがあるかもしれない。
しかし実際には 現在の量子コンピューターは 非常に単純な 15 = 5 × 3 の因数分解しかできないのである。
しかも この因数分解は 量子もつれ (エンタングルメント) や "重ね合わせ" とは何の関係もない手法によるものである。
( 後で説明するが、この手法は 古典的な磁気モーメントの相互作用を用いたにすぎない。)
(Fig.1) 古典的なコンピューター?
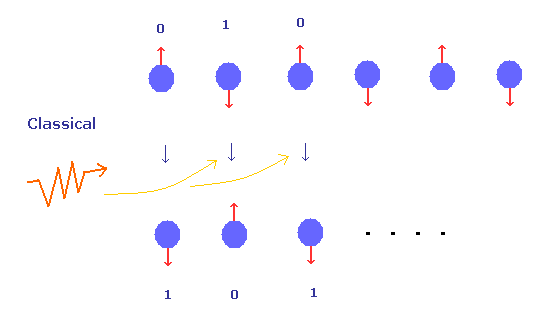
Fig.1 では、 N 個の粒子が並んでいる。
"0" もしくは "1" の各番号は 各粒子の 2つの異なったエネルギー準位や 磁気モーメントの方向を表している。
( この2つの異なった状態を "qubit" もしくは "量子ビット" と呼ぶ。)
通常の古典的なコンピューターでは、それらの番号を変更するには 各粒子すべてに操作をする必要があるため、N 回の操作が必要になる。
操作とは レーザーなどによる照射などのことである。
(Fig.2) 重ね合わせ = 量子並列計算 ?

量子力学によれば、すべての粒子は ミステリアスな重ね合わせの状態にある。
そのため たった1回の操作で、すべての粒子を同時に変化させることが可能である (= 並列計算。)
彼らは しばしばこの論法を引き合いにだすが、実際にこの超自然的な計算を達成した量子コンピューターは存在しない。
”量子コンピューター”のフレーズや アルゴリズムの理論のみが 一人歩きし、実験結果が まったく伴っていないのが現状である。
(Fig.3) 重ね合わせ = 単に古典的に振動しているだけ。

現在 陽イオン、ジョセフソン接合、NMR、マッハ・ツェンダー干渉計などを用いた様々な量子装置 (= qubit ) が存在する。
しかし それらすべての手法は 現在すでに限界に達しており、もちろん高速計算する能力はまったくない。
( フッ素を含む分子と NMR を組み合わせた方法で 15 = 5 × 3 の簡単な因数分解はできるが、この手法は 古典的な磁気モーメントの相互作用を用いたにすぎない。)
重要な点は これらの量子装置は ミステリアスな重ね合わせのパワーを まったく示していないということである。
例えば、通常の電磁波照射で qubit のエネルギー状態を 周期的に変化させているにすぎない。
そして 単に異なった状態が混合した状態を 奇妙な重ね合わせと表現しているにすぎないのである。
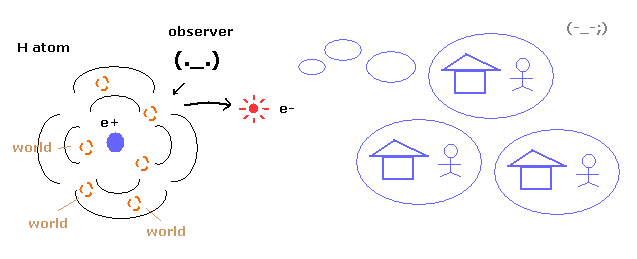
(Fig.4) 重ね合わせ = 非現実的な多世界。
もし ミステリアスな "重ね合わせ" に基づく量子コンピューターを実現しようとするならば、私達は 波動関数の重ね合わせが実際 何なのかを最初に知る必要がある。
なぜなら この重ね合わせそのものが間違っているとしたら、それはつまり 私達は 単なる幻想を追っていることになるからである。
量子力学によれば、私達が 粒子を観測しようとした瞬間に 全空間に広がった波動関数が 点状粒子に収縮(収束)することになる。
この過程は 一瞬なので超光速 (= 非局所性 ) である。そのため 非局所性を避けるために 私達は 奇妙な多世界解釈を採用するしか方法はない。
多世界解釈では、粒子を観測することは 異なった状態の粒子を含む無限の世界の中の 1つを見ることと同じである。
(Fig.5) 単一の C60 フレーレン分子は自分自身と干渉できる。

単一の C60 フレーラン分子でさえ 自身と干渉することができる。
2重スリットにおける 単一の粒子の干渉を説明するために、量子力学は 超光速の波束の収縮を避けるために "多世界解釈" (= 重ね合わせ ) を必要とする。
もちろん、多世界理論は あらゆる可能性の状態を必要とするため、その中では 世界の数は 非現実的に ∞ × ∞ × ∞... のペースで増加することになる。
つまり この理論は 一言で言ってあり得ないものであり、波束の収縮機構に関する解釈が作りすぎである。
リアルなドブロイ波に基づくボーア模型は Fig.5 左に示すように この干渉現象を自然に説明できる。
量子力学でありながら リアルな粒子の動きを主張する ガイド波理論 (= ボーム解釈 ) というのもある。
(Fig.6) ガイド波理論は 様々な原子の電子運動を説明できない。
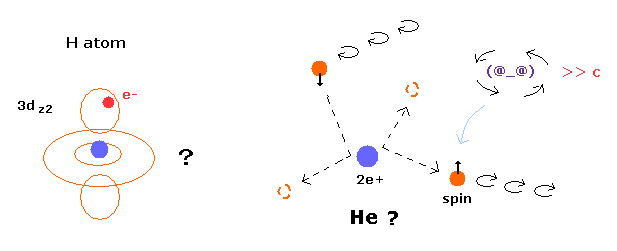
Fig.6 左は 水素原子の 3d 状態の確率密度を示したものである。
もちろん、シュレディンガーの水素原子は クーロンの関係式に依存しているため、その電子は クーロンの関係式に従わなければならない。
しかし もし 3d 状態の電子が クーロン力に従って運動するとしたら、それは Fig.6 左に示すような複雑怪奇な運動はとれない。
さらに、ガイド波理論は 2電子原子であるヘリウム内の電子運動に関してまったく説明することができない。
なぜなら ヘリウムの2つの反発する電子は 容易にカオス状態になり 自己イオン化してしまうからである。
このページに示すように、1920 年代当時 3体問題である ヘリウム原子を リアルな電子の運動で説明できなかったからこそ 彼らは奇妙な確率解釈を選択せざるを得なかったのである。
( もし水素原子だけしかなかったら、ボーア・ゾンマーフェルト模型のほうが 自然な説明ができる。)
(Fig.7) ガイド波理論 = 超光速のシグナル。
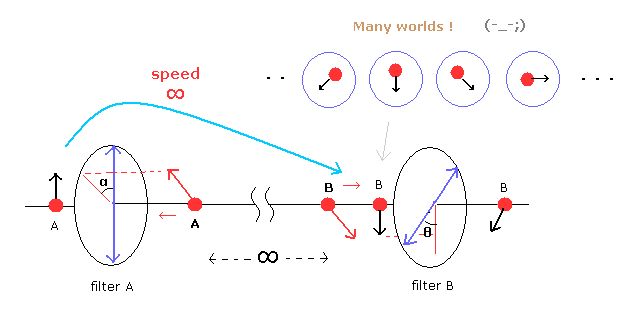
あなたがたは ベルの不等式の破れは アインシュタインによって提唱された隠れた局所変数を否定したというフレーズを しばしば聞いたことがあるも知れない。
Fig.7 では、光子 (= A ) が フィルター A を通過して その偏光軸を フィルター A と同じ向きにそろえた瞬間に もう1つの光子 B の偏光軸も どんなに離れていようが フィルター A と同じになることを意味している。
つまり 2つのもつれた光子間のシグナルは 超光速で伝わっていることになる (= 非局所性 )
この超光速のシグナルを回避するために、彼らは 多世界解釈に頼るしかなかったのである。
もし 実在のガイド波理論を採用すると、超光速のシグナルを リアリティーとして受け入れなければならない。
このページに示したように、もし 古典的な電磁波を用いれば、この破れを 局所性かつ現実的に説明することが可能である。
( もちろんのことだが、光子という粒子を諦めることは 量子力学と量子電磁力学そのものが間違いであることを意味する。 )
(Fig.8) すべての解釈は不自然。 → "Shut up and calculate !"

多世界や ガイド波などの具体的な解釈を主張している方々は ある意味 正直である。
無限の多世界は非現実的で、ガイド波は クーロンの相互作用に従わない。
どの解釈も不自然なので ほとんどの物理学者達は 単なる "Shut up and calculate" 解釈、いわゆる 「これ以上つっこまず 黙って計算だけしてろ!」という姿勢を取っている。
この "Shut up and calculate" は いわゆるコペンハーゲン解釈に相当し、その中で 彼らは波動関数 (= 重ね合わせ) の正体自体を問うことを諦めて ただ計算だけしていればいい としている。
しかし 波動関数そのもののメカニズムの追及を諦めて 量子コンピューターの研究を進めることは 非常に危険である。
なぜなら 彼らが目指しているものが 単なる幻想であるかもしれないからである。
お気づきかもしれないが、波動関数そのものの正体を追及せず 何らかのブレイクスルーを期待すること自体 不可能なことである。
(Fig.9) 電子の回転速度 ?
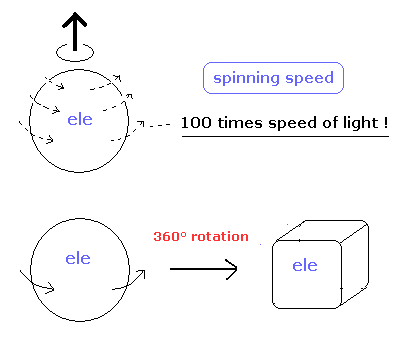
もし電子のスピンが 実際に回転によるものとしたら、このページに示したように、そのスピン速度は 光速の 100 倍以上になる。
また スピン回転する電子は 1回転では 元の状態に戻れない。2回転で戻る。
つまり スピンという概念自体 現実のものではないのである。
そのため すべての物理学者が この奇妙なスピンとは何かを問うことを諦めており、この姿勢が 科学の発展を妨げていると言っていい。
(Fig.10) 電子スピン (= ボーア磁子 ) = 円運動 (= ボーア磁子 ) ?
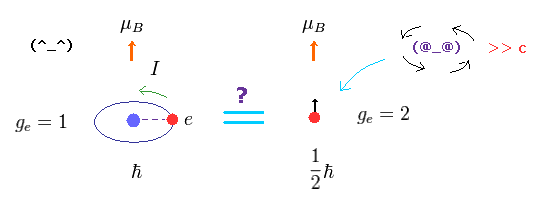
このページに示したように、 磁気モーメントは 電流 I × 電流のループの面積 (= πr2 ) である。
驚くことに、量子力学的スピンも ボーアの基底状態の円軌道と 同じ磁気モーメント (= ボーア磁子 ) を持つ。
このトリックは 電子のg因子 = "2" に存在する。
結果的に、磁気モーメント = g因子 × 角運動量 = 2 × 1/2 = 1 (= ボーア磁子 ) となる。
最も重要な点は このボーア磁子は ボーア軌道に純粋に由来するもので 量子力学そのものから得られるものではない。
結論からすると、電子や原子核などの粒子の 奇妙なスピンのすべては 何らかの実在の回転と見なすことが自然である。なぜなら "Shut up and calculate !" は 真の理論には 決して なり得ないからである。
(Fig.11) 2つの "Shut up and calculate !" が コンピューターの発展を妨げている。

お気づきかもしれないが、波動関数やスピンの より深いメカニズムの解明自体を諦めて 量子コンピューターの発展を目指すことは 矛盾している。
各粒子の位置と速度を 正確に操作できなければ、私達は それらの相互作用を操作し、量子コンピューターの発展を成し遂げることはできない。
もちろん、位置と速度を同時に知ることは 量子力学の不確定性原理が間違いであることを意味する。
(Fig.12) トラップされた Be+ イオンの超微細構造。

最初に パウルトラップ内で 振動する ベリリウムイオン ( Be+ ) をベースにした qubit について説明する。
様々なイオントラップに基づく量子コンピューターは 今だに実現していないため それらの理論のみ 独り歩きしている状態である。
核のスピン (= 回転 ) を考慮すると、Be+ イオンの価電子 2s1/2 は 2つの超微細構造状態 ( up と down ) に分離する。( このページも参照のこと。)
また イオンの運動やクーロン相互作用も考慮して 非常に小さいエネルギー準位差も作りだす (= フォノンモード 1 もしくは 0 )。
また 彼らは しばしば 2つのトラップされた Be+ イオンは 互いにもつれた状態になり得ると主張している。
しかし これらイオンの距離は 数μm と非常に短い。
そのため 2つのイオンのもつれは 局所性のループホールのため 本当ではない。
( 端的に言えば、それらは 電磁波照射によって 古典力学的にただ振動しているだけで エンタングルメントとは関係はない。)
(Fig.13) 角運動量ゼロ (= s 状態 ) → Shut up and calculate !
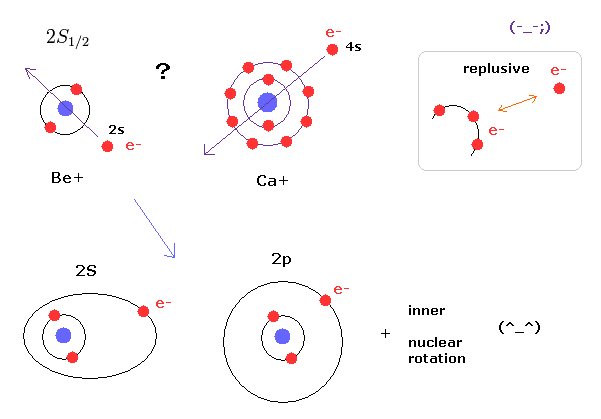
実際 角運動量ゼロの 2s1/2 状態を過程した瞬間に 私達は "Shut up and calculate !" の解釈を受け入れたことになる。
なぜなら 常識的な視点では、電子は 強いクーロン反発力のため 内殻の電子群を貫くことができない。
この奇妙なゼロの角運動量を認める代わりに、外殻の電子が 内殻の電子群の周囲を周っていると考えたほうが 極めて自然である。
このページに示したように、もし楕円もしくは円軌道を考慮すれば、2s と 2p のエネルギー準位差を説明することができる。
さらに 水素原子と異なり、Be+ や Ca+ イオンは 内殻の電子群の磁気モーメントを持つ。
自然な軌道、内殻の電子、核の回転によって "Shut up and calculate !" せずに すべてのスペクトラムの結果を表すことができる。
(Eq.1) 2つの Be+ イオンの 4つの異なった状態。
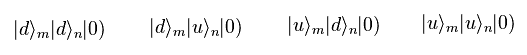
最初に 4つの異なった状態を用意する。2つの Be+ イオン "m" と "n" は 超微細構造で up もしくは down のエネルギー準位の状態である。
そして "フォノン" のエネルギーモードをゼロとする。
( このフォノンは 非常に曖昧な概念であるため、イオンの運動パターン+クーロン相互作用のようなものと考えておけばよい。)
(Eq.2) 右円偏光の光の照射

ここで "m" の Be+ イオンに 右円偏光 (= π パルス ) の光を照射すると、その超微細構造状態と フォノンモードは Eq.2 のように変化するとする。
π パルスのために、位相因子 "i" が付け加えられている。
Be+ イオンそのものの位相を知ることはできない。照射する光やその照射時間から推定するだけである。
( この位相は 振動中の ある状態と考えておけばいい。)
Eq.2 の照射後、Eq.1 の4つの状態は
(Eq.3)
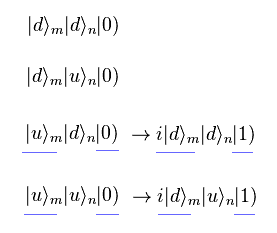
次に それらに "2π" パルスレーザーを照射する。それは π パルスレーザーの2倍の照射時間である。
そのため "2π" パルスレーザーの照射後、Be+ イオンの位相に "-1" の因子が付加される。
"n" の Be+ イオンを 左偏光の 2π パルスレーザーで照射すると 次の変化が起こるとする。
(Eq.4)
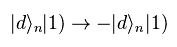
ここで フォノンの状態が 2つの Be+ イオンの両方に影響を与えるとする。
結果的に Eq.4 の照射後に Eq.3 の状態は
(Eq.5)

そこでまた "m" のイオンに 右偏光の光 ( π パルス ) を照射する。
すると Eq.2 のように
(Eq.6)

結果的に Eq.5 の状態は
(Eq.7)

Eq.7 に示すように、up と up の超微細構造の位相のみ 負の状態になる。
ここで 次の ± 状態を指定する。
(Eq.8)
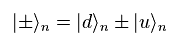
Eq.7 と Eq.8 から、 次を得る。
(Eq.9)
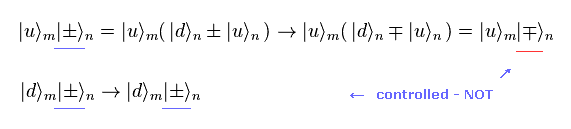
Eq.9 に示すように、 "up" の状態のみ ± の状態が変わる。
この操作を "制御-NOT" ゲートと呼び、コンピューターの基本となるものである。
しかし 不安定性や 非常に短いデコヒーレンス時間 ( 0.1 秒 ) などの様々な問題により この Be+ イオンの操作を 通常のコンピューターに適用することができない。
つまり 量子コンピューターについての現在の研究は この時点で すでに限界に達しているのである。
(Eq.10) 量子もつれ?

Eq.9 を用いて、Eq.10 の状態を生成することができる。
Eq.10 では、 2つのペア ( up, + ) と ( down, - ) が生成された。
そのため 彼らは この状態をミステリアスな量子もつれの状態だと主張しているのである。
( このケースでは up の状態が + の状態とエンタングルしている。)
しかし上で説明したとおり、この状態は 超光速のエンタングルメント状態とは何の関係もない。
これらの状態を 通常の古典的な操作で生成したにすぎない。
( どうも彼らは すべてのものを エンタングルメントにつなげようとしている。)
また Be+ イオン間の距離は非常に短いため、局所性ループホールが存在する。
つまり 2つのイオンは 通常の古典的な照射でコントロールされているにすぎない。
(Fig.14) キュービット分子。
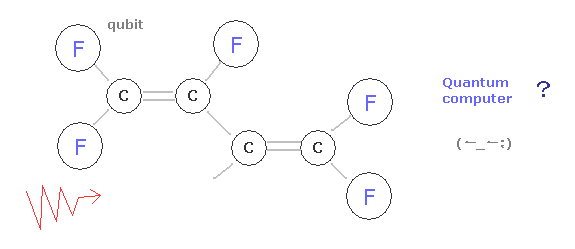
Fig.14 の分子は いくつかのフッ素原子と炭素原子でできている。
各原子核の磁気モーメントと 電子と原子核間の相互作用のため、そのエネルギー準位は 非常に小さな間隔に分かれる。
これらの異なったエネルギー状態、核磁気共鳴 ( NMR )、何かしらのアルゴリズムを用いて、彼らは 15 = 5 × 3 の因数分解を行った。
しかし 他の量子ビットと異なり、この方法では 非常に多くの分子の集合からの 平均の NMR スペクトラムしか得ることができない。
彼らは 各量子ビット (= 原子 ) を個別に操作したり、量子もつれを利用することもできない。
つまり この手法は いくつかの異なったエネルギー状態と NMR を用いただけで、”重ね合わせ”とは何の関係もない。
各原子の様々な運動のため、7 キュービット分子を用いた 15 = 5 × 3 の因数分解が 限界である。
(Fig.15) セシウムの微細構造 + 偏光
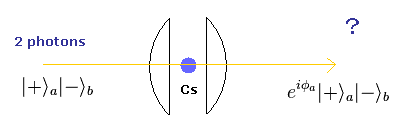
Fig.15 では、 マイクロキャビティー内の セシウム (Cs) 原子が 左 (-) もしくは 右 (+) 偏光の光で照射されている。
ここで 右偏光の光のみが セシウムの微細構造のエネルギー状態と相互作用できるように 装置をセットアップする。
( つまり このケースでは キュービットは Cs の微細構造の2つのエネルギー準位ということになる。)
次の4つのパターンの2つの光子を キャビティーに送ると、
(Eq.11)

Csとの相互作用に応じて 様々な光子の位相を得ることができる。
δ が 180 度のとき、Be+ イオンのときのような 制御-NOT ゲートを得ることができる。
しかし この基本的な NOT ゲートですら この手法では実現していない。
また、左もしくは右円偏光の光は 明らかに古典的な電磁波であり 光子という粒子とは何の関係もない。
(Fig.16) マッハ・ツェンダー干渉計とジョセフソン結合。
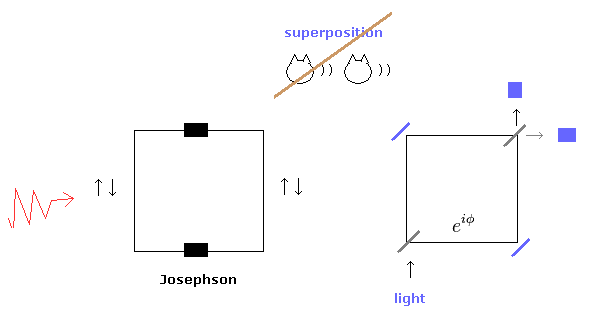
Fig.16 左では、ジョセフソン結合を含んだ 超電導回路を用いて、彼らは異なったエネルギー準位を得ようとしている。
彼らは しばしば これらの状態は 奇妙な"重ね合わせ状態"と主張しているが、はっきり言って 単に 異なった古典的な動きが 混ざり合っている状態にすぎない。
Fig.16 右では、マッハ・ツェンダー干渉計において ビームスプリッターと干渉効果を用いて 様々な位相の電磁波を得ようとしている。
ここでも 彼らは この状態は 量子力学的重ね合わせ状態だと主張しているが、単に古典的な電磁波の干渉パターンを示しているにすぎない。
また これら2つの手法ともに 量子コンピューターとしては まったく実現していない。
(Fig.17) 平行世界 = 重ね合わせ は幻想である。

上のセクションで述べたように、どの量子キュービットも 量子の"重ね合わせ"に特異的な能力を 全然発揮していない。
"平行世界" や "量子もつれ" などの魅惑的なワードが 実態とかけ離れた状態で 人々を引きつけているだけのように見える。
"重ね合わせ" をベースとした 現在の量子コンピューターに関する研究は はっきり言って 完全に行き詰まっている。
これらの深刻な現実は 彼らが 本質的に間違った 架空の状態を追っていることを 強く示唆している。
(Fig.18) "クーパー対" は 実在するのか??
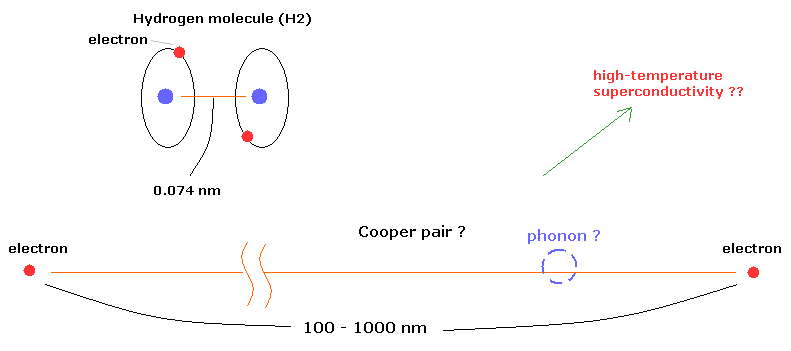
現在の物性物理学によれば、クーパー対は 低温状態において 非常に曖昧な存在である "フォノン" というものを介して結合するとされている。
驚くことに クーパー対の2つの電子間の距離は 何と 100 - 1000 nm (ナノメーター) もあるのである。
例えば、水素分子 (H2) の 核間距離は 約 0.073 nm である。
どうやって、これら2つの電子は 超伝導体の中で 安定して結合できるのだろうか?非常に奇妙である。
標準的な解釈によれば、正電荷の原子核などが これら非常に長い結合に 準粒子 フォノン として関わっているそうである。
( しかし、私にはこの長すぎる結合が 非常に不自然に思われてならない。あなたがたはどう思われるだろうか?)
BCS 理論によれば、非常に低温において 超伝導体中に クーパー対が形成されるとされる。
そのため 現在の BCS 理論は 高温超伝導を説明することができない。
(Fig.19)
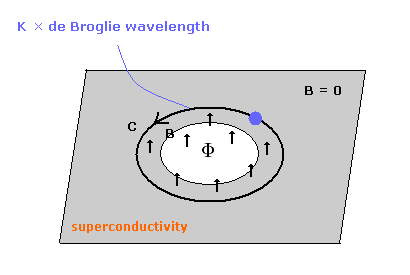
クーパー対を支持する重要な事実の1つに 磁束量子 (= Φ0 ) というものがある。
超電導リングを通過する際に 磁束 (Φ) が量子化されることが知られている。
(Eq.12) 磁束量子
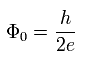
このページに示したように、彼らは この磁束量子をクーパー対を用いて説明しようとしている。
もちろん 奇妙なスピンも 彼らが クーパー対を必要とする理由の1つである。
なぜなら スピン 1/2 のフェルミ粒子が そのままの状態で存在していたら、ボソン様の性質を示せないからである。
クーパー対が形成されることによって この スピン1/2 の効果がキャンセルされると 彼らは主張している。
ここで 電子が Fig.19 の穴の周囲近くを 磁場をキャンセルさせるために回っていると仮定する。
遠心力が ローレンツ力に等しいことより、
(Eq.13)
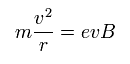
その軌道1周が ドブロイ波長の整数倍 (= K ) に等しいとき、
(Eq.14)
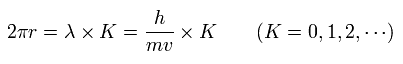
ここでは λ = h/mv。
Eq.13 と Eq.14 から、次を得る。
(Eq.15)
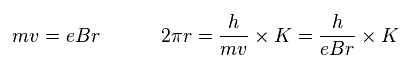
そのため
(Eq.16)
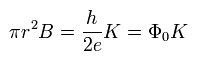
Eq.16 は Fig.19 の穴を通過する 磁束 (Φ) である。
( πr2 は この穴の面積である。 )
結果的に "実在の"ドブロイ波を用いて 超電導の磁束量子を得ることができた。
(Eq.12) 磁束量子。
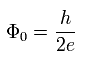
また ここでは クーパー対は必要ない。
もちろん、クーパー対が存在しなければ、高温超電導のような問題も 最初から存在しない。
( 彼らは この問題を ひも理論の共形場理論を用いて解決しようとしているが、この手法には 何のリアリティーもない。 )
ジョセフソン効果とは 薄い絶縁体によって隔たれた 超電導体の間を 電流が流れる現象である。
この 2つの超電導体が 非伝導体バリアによって結合しているものを "ジョセフソン結合" と呼ぶ。
1962 年に、ジョセフソンが この効果を予想し、それは SQUIDs などの 量子力学的な circuit で重要な意味を持つ。
ジョセフソン結合のバリアはとても薄いため、弱い刺激を与えれば 電流が流れることができる。
しかし 超電導体などの 無磁場 の状態でさえも このバリアに電流が流れる。(量子トンネル効果。)
もし ド・ブロイ波 によって この量子トンネル効果を説明できれば、このことは ボーア模型によって ジョセフソン効果と量子トンネル効果を説明できる ことを意味する。
(Fig.20) ジョセフソン結合。

直流ジョセフソン効果とは トンネル効果によって 電磁場が存在しない状態でも 絶縁体間を直流電流が流れる現象である。
(もちろん、超電導の磁場をゼロにするのは 穴付近の電流は Φ をキャンセルするために存在する必要がある。)
この 直流ジョセフソン電流は 次のように 絶縁体を挟んだ位相差の sine に比例する。
(Eq.17)
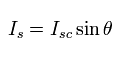
ここでは 位相差 θ は次のように表せる。
(Eq.18)
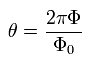
Eq.17 と Eq.18 は 穴の部分の磁束 (Φ) が 磁束量子の整数倍のとき、位相差がゼロになり ジョセフソン電流が生じない。
つまり、我々は ジョセフソン結合は 穴付近の電子のド・ブロイ波の影響を受ける と主張することができる。
よって、量子トンネル効果とは 電子の ド・ブロイ波によって生じるものなのである。
接合間の電位 V を固定すると、位相は 時間とともに 直線状に変化し、電流は交流になる。
(交流ジョセフソン効果.)
マクスウェル方程式によれば、 Fig.20 のリングの電位は次のように表せる。
(Eq.19)

ここでは Eq.18 を使っている。
Eq.19 を 時間 t で積分すると 次を得る。
(Eq.20)
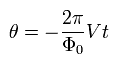
Eq.20 を Eq.17 に代入すると、 次の 交流ジョセフソン電流を得ることができる。
(Eq.21)
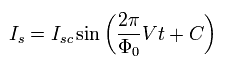
Eq.21 の振動数 は
(Eq.22)
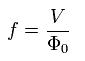
Eq.22 の 振動数は これと同調する マイクロ波で確認することができる。(シャピロステップ。)
そして、この測定された 電圧 (V) は 電圧標準の定義として使用される。
また ジョセフソン効果は Φ0 に プランク定数 (h) が含まれているため、その定義にも使われる。
(もちろん、このプランク定数は 電子の ド・ブロイの関係式に由来している。)

2013/2/1 updated This site is link free.