ボーアの3電子原子(イオン) において、我々は、水素様原子の方程式を使って、2S 電子のエネルギーを計算し、正確な結果をだすのに成功した。
ここでは、内殻の 1S 電子が 2S 電子に比較してかなり原子核に近づいているとしたからだ。
(例えば、ボーアの 炭素イオン C3+ ページ に示したように、中心の正電荷を +4e =+6e -2e と仮定した。)
しかし、実際には、内殻の1S 電子は 原子核から少し離れている。
(炭素の場合は、約 930 MM (1 MM = 10-14 meter) 原子核から離れている。)
そのため、もし”実質的な”中心の正電荷を少し大きくしてみると (炭素の場合は、+4.0e の代わりに、+4.25e した)、価電子の運動を正確に表現することができた。
これらの C3+ と、中性の炭素の場合の違いは何なのだろうか?
ここでは、3電子原子(イオン)の 代表として、炭素イオン (C3+) を使う。
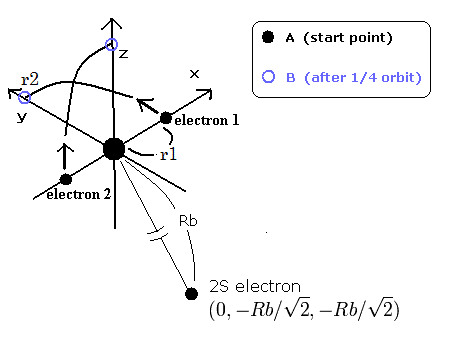
Fig.1. 3電子原子 (イオン). C3+, Li, Be+, B2+ ....

ボーアの C3+ のページに示したように、我々は Fig.1 の スタート地点 (start point) において、水素様原子のエネルギーの式を使用した。
ところで、スタート地点 と 1/4 周した後の地点 における 2S 電子に影響を与える ”実質的な”中心の正電荷 はどれくらいであろうか?
Fig.2. ”実質的な”中心の正電荷の変化。
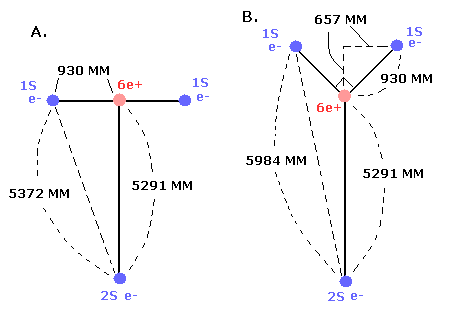
C3+ の場合、我々は 原子核と 2S 電子の間の距離を 5291 MM とした。(このページ参照のこと。)
(また、6e+ の炭素原子核と 1S 電子の間の距離は、約 930 MM であることがわかった。)
そのため、スタート地点 (=A) では、2S電子に影響を与える”実質的な”中心電荷は、次のようになる。
(比較のため、ここでは 2S 電子と他の粒子間の 位置エネルギー を計算する。)
Eq.1. スタート地点 (A) における”実質的な”中心の正電荷.
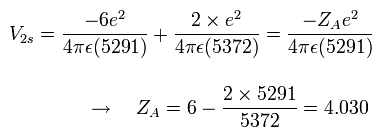
Eq.1 に示すように、1S 電子が 6e+ の原子核から少し離れていることを考慮すると、”実質的な”正電荷は 位置エネルギー V に関して、少し +4e より大きくなる (+4.030)
また、”実質的な”中心の正電荷がが少し大きくなると、次に示すように 軌道半径は少し 短くなる。
Eq.2. 中心の正電荷が "z" のときの半径。
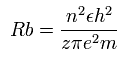
そのため、エネルギーは次のように z × z に比例してさらに低くなる。
Eq.3. 中心の正電荷が "z" のときのエネルギー。
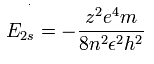
結果として、スタート地点 (=A) における 本当の”実質的な”中心の正電荷は 次に示すように +4.06 になる。
Eq.4. スタート地点 (A) における 本当の”実質的な”中心の正電荷.
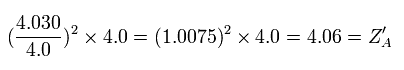
もし、+4.0 のかわりに この +4.06 を使うと、エネルギー変化量は次のようになる。
(ここでは C3+ の 2S 電子のイオン化エネルギー (= 64.49 eV) を例として使う。)
Eq.5. スタート地点 (A) におけるエネルギー変化量。
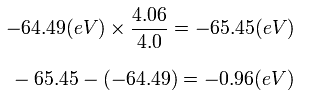
つまり、スタート地点 (A) において 1S 電子が核から少し離れたことを考慮したときの エネルギー変化量は、わずか 0.96 eV である。
(もちろん、リチウム原子では、2S 電子と核との距離がもっと長いため、この誤差は さらに小さくなる。)
1/4 周した後の地点 ( Fig.1, 2 の B ) ではどうであろうか?
この B 地点では、位置エネルギーに関して ”実質的な”中心の正電荷は次のようになる。(Fig.2 参照のこと。)
Eq.6. 1/4 周後の地点 (B) における”実質的な”中心の正電荷。
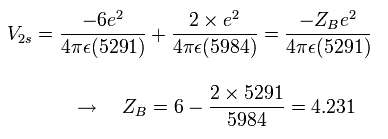
そのため B 地点において、”実質的な”電荷は +4.0e のかわりに +4.231e となる。
さらに 我々は 短くなる 半径の影響 (Eq2. と Eq.3) を考慮する必要がある。
Eq.7. 1/4 周後の地点 (B) における 本当の”実質的な”中心の正電荷。
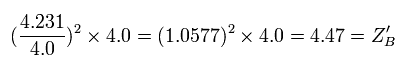
結果として、1/4 週後の地点 (B) における 本当の”実質的な”電荷は +4.47e となる。
炭素イオン (C3+) の場合は、スタート地点 (A) において、水素様原子の式を使用した。
Eq.5 に示したように、この近似方法による 誤差 はとても小さい。
このことが、ボーア模型の3電子原子(イオン)において、我々がほぼ正確な結果をだせた理由である。
(C3+ における計算結果は -944.7 eV で、これは実験値 -946.574 eV にほぼ等しい。)
この後、2つの 1S 電子は原子核の周囲を 2S 電子を避けるように周回していく。(Fig.1)
一方で、中性の炭素においては、1S 電子のかわりに 2S 電子の”全体的な”動きを考える必要がある。
そのため、”実質的な”中心電荷を 平均化する必要がある。
(中性の炭素では、+4,0e のかわりに +4.25e を使用した。 この値は 上記の +4.47e と +4.06e の間の値である。)
これが、我々が 中性の炭素原子においても 正確な結果をだせた理由である。
----------------------------------------------------
上で述べたように、水素様原子の式を用いて、我々は いろんな3電子原子(イオン)の基底状態のエネルギー計算に成功した。
ところで、1S 電子が その軌道の 1/4 軌道を進む間に、2S 電子は 自身の軌道のどれくらいを進むことができるのだろうか?
C3+ において、2 × 1S 電子の全エネルギーは、-392.087 (5th イオン化エネルギー) -489.993 (6th) = -882.08 eV となる。
また、C3+ の 2S 電子の全エネルギーは -64.49 eV (4th) である。
ビリアル定理によると、運動エネルギー (T) と 全エネルギー (E) は、T = - E の関係式を満たす。
そのため、1S と 2S 電子の速度比は、次のようになる。
Eq.8. 1S と 2S 電子の速度比 (C3+)
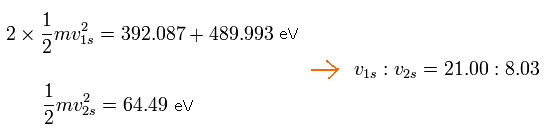
上で述べたように、C3+ の 1S 軌道の半径は 930 MM である。(1軌道 = 2π × 930)。
1S 電子が その軌道上の 1/4 を進む間に、2S 電子は 次の示すように 558.58 MM 進むことができる。
Eq.9. 1S 電子が 1/4 周 進む間に 2S 電子が進む距離。
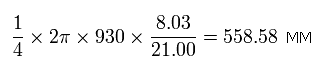
2S 電子の平均半径は 5291 MM であり、つまり 2S 軌道の1周分の距離は 次のように 33243.35 MM となる。
Eq.10
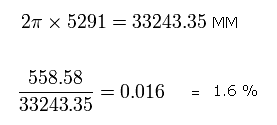
つまり、2S 電子 が この間 (= 1S が 1/4 周する間) に進む移動距離 (= 558.58 MM) は、2S 軌道の たった 1.6 % である。
この結果は、3電子原子(イオン)の軌道を計算するときに Fig.1 のように近似的に 2S 電子の位置をほぼ固定して考えてもいいことを示している。
このことも、3電子原子(イオン)において、我々がほぼ正確な結果をだせた理由の1つである。
1S と 2S 電子の公転周期は違う。
そのため、Fig.1 の Rb は スタート地点において、ある時期では 5291 MM よりも短くすることができる。
しかし、この場合は、Eq.3 の水素様原子のエネルギーの式を少し変更する必要がある。
例えば、2S 電子の”全体的な”運動を考えるとき、我々は 3つの粒子 (= 2 × 1S 電子 と 6e+ 核) を 1つの点粒子 に近似的に凝縮させなければならない。
(これらの3つの粒子を分離したまま 2S 電子の運動を計算するのはかなり難しいからである。)
2つの 1S 電子が 6e+ 核から分離したとき、2S 電子に影響を与える ”実質的な”中心電荷は変化する。
位置エネルギー (V) の変化を計算することによって、我々は この中心電荷の変化を推定することができる。
しかし、Fig.3 に示すように、中心電荷 4.0e+ が変化しないまま、2S 電子と中心電荷の距離が 短くなった場合も、位置エネルギーは低くなる。
この Fig.3 の場合を除外する方法はないだろうか?
Fig.3. 4.0e+ 電荷は変化しないまま、位置エネルギーが低下する場合。
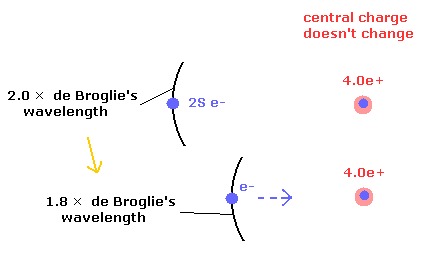
Fig.3 では、そのかわりに 2S 軌道に含まれる ド・ブロイ波の数が 2.0 未満 になる。
つまり ド・ブロイ波の視点から、これらの状態を 区別して考えることができるといえる。(もちろんあくまで近似的に。)
1S 電子が 6e+ 原子核から分離したときに、それらは 2S 電子から遠ざかる方向へ離れる。
一方で、6e+ 原子核は 2S 電子に少し近づく。
結果として、3つの電荷 (= 2× 1S 電子 + 原子核 ) の中心 は変化しない。(Fig.4)
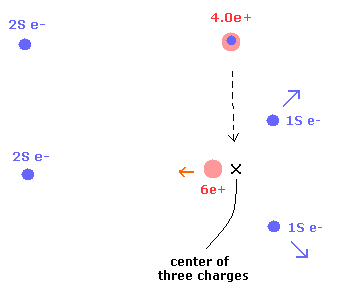
Fig.2 (Eq.1, Eq.6) では、2S 電子と 6e+ 原子核 は 動いておらず、1S 電子だけ 2S 電子から遠ざかる。
そのため Fig.2 (Eq.1, Eq.6) では、3つの電荷の中心が 2S 電子の逆の方向へ少し移動する。
Eq.1 (Fig.2 A) においても、1S 電子の分離の影響で、3つの電荷の中心は少し 2S 電子の逆方向へ移動する。 =この3つの電荷は空間に広がる。
(ここでは、3つの粒子の位置に加えて、クーロンの関係の 1/r の影響も考慮しなければならない。)
そのため、この3つの電荷の中心を元の位置に戻す必要がある。
Eq.2 は ド・ブロイ波の観点から、この位置を調整するもので、これを使って 1S 電子が遠ざかるにつれて 2S 電子を少し原子核に近づける。
結果として、3つの電荷中心と 2S 電子の”実質的な”距離は変化せず、我々は 真に増加した”実質的な”中心電荷の増加量に集中することが可能になる。
Fig.5. ”空間的に離れた”粒子の効果を含む点粒子。
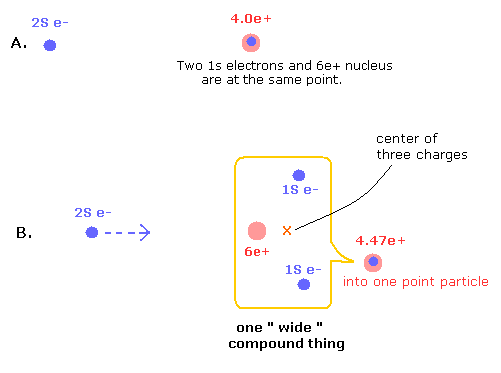
B の状態では、1S 電子は 2S 電子から遠ざかっている。その影響で 2S 電子が原子核に少し近づいている。
この Fig.5 B の状態は Fig.4 の下の図の状態と同じである。(Fig.4 では、かわりに 6e+ 原子核 が 2S 電子に近づいている。)
(この点粒子の原子核は、1つの空間的に広がりを持った複合体 (one "wide" compound thing) とは違うことに注意。)
ここで、Fig.3 の A と B における位置エネルギーの比を計算し、その比から、この複合体のおおよその電荷を推定する。
そして、最後に、この 空間的な広がりをもった複合体を 1つの点状の粒子と みなす。 (+ Fig.1,2 の A と B の結果を平均化する。)
つまり、B においては、この凝縮の代償として、この複合点粒子の電荷が増加したことになる。

2011/1/9 updated This site is link free.