直下の“検索イン時クリック”をクリックして頂くとページ全体が表示されます。

幾何公差 ３．１５－１/２ 最大実体公差方式（まるＭ）　 　最近最大実体公差方式が入っている図面が増えたような感じがありますので、なるべく専門用語を使用しないで説明しようと思います。もしかしたら解釈が違うかも知れないのでＪＩＳ規格のＪＩＳＢ００２３を参照することをお奨めします。 ※ここでは説明＆理解し易いように一方向だけの説明になります。 　 　最大・最小実体公差方式はボーナス公差とも言われ、幾何公差の緩和とコスト低減等を目的としているようです。造る側としては 最大実体公差は頭に入れず、不幸にも完成品が公差値から外れた場合の救済に使用した方がいいいと思います。 １．軸物で公差値だけにまるＭがある場合　 １）図示例 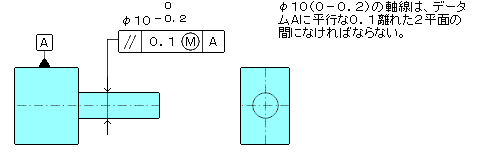　　※通常の位置度に緩和領域が追加された図面です。　 ２）解釈例 ア、実効寸法 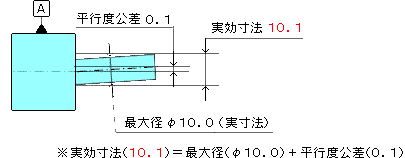　　　※上図のように軸の最大径と平行度の公差で実効寸法が決まります。様はその軸 　　　　が許容される円筒の最大値（φ１０．０）と公差値（０．１）の大きさで決まります。 イ、実際の軸径がマイナスいっぱい（１０－０．２）の場合の緩和された平行度公差 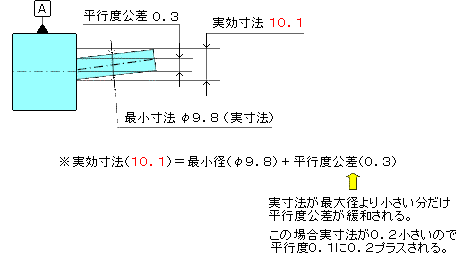ウ、動的公差線図 　上記で説明した最大実体公差の変動する範囲を表にしたものです。 ※横軸は軸の直径を、縦軸は平行度を表し、軸径と平行度が交わる点が公差領域 　　内なら合格で範囲外なら不合格になります。 　　　例　軸径１０．１で平行度０．０５の場合、軸径が大きいのでＮＧ 　　　　　　軸径９．８５で平行度０．３５の場合、平行度が公差外なのでＮＧ 　　本来の許容差は水色で、黄色い部分はボーナス（特別）公差とも言われます。 ２．要素が穴で公差値とデータムに最大実体公差がある場合 １）．図面例　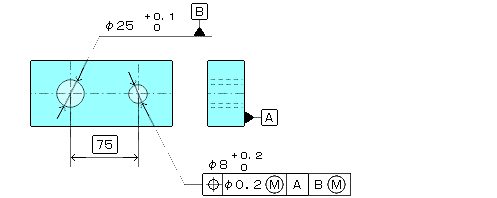 前へ  次へ トップ→幾何公差→●３．１５－１/２ 最大実体公差方式（まるM） © 2000　natuo