
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。数学上の産物。
現在の物理の教科書が分かりにくい理由。
(Fig.1) "無数の" 重いヒッグス粒子は 本当に飛び交って すべての物に質量を与えているのか?

私達は しばしば "加速器内で ヒッグス粒子が実際に見つかった" というビッグニュースを耳にする。
しかし 今一度ここで この粒子の リアリティー と 有用性について 冷静に振り返ってみる必要がある。
あたりまえのことだが、目の前に 何か分からないことがあるなら それについて何なのかと問うことが 科学の基本姿勢である。
また 科学というのは もしそれがリアルに正しいとしたら いつか私達の生活に 自動的に役に立つものである。
このページに示したように、彼らは 無数のヒッグス粒子が 私達の周囲を 飛び交っていると主張しているにも関わらず、肝心なヒッグス粒子そのものは 何兆回もの衝突で やっと1つできるかできないかの低確率なものなのである。
( それらのほとんどは 無数のノイズである。 )
さらに ヒッグス粒子そのものは 直接的には観測することができず、最終産物であろう 光などから その存在を推定しているだけにすぎない。
(Fig.2) -1/3、 +2/3 などの分数電荷は リアルなものなのか?
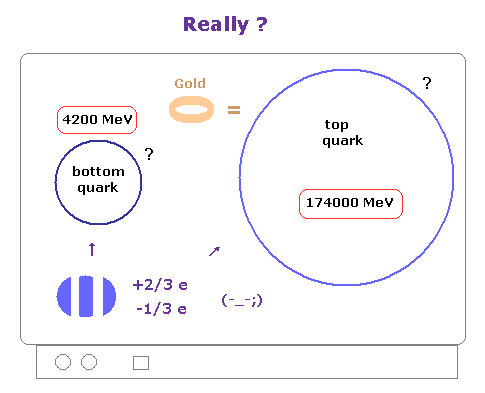
私達は -1/3 や +2/3 などの 分数電荷を持つクォークが 実際に見つかったというコメントを よく目にする。
ご存じのとおり、これらの説明は かなりの誇張であり 完全に間違いである。
なぜなら 分数電荷そのものは 見つかっておらず、そもそも 彼ら自身が クォークやグルーオンは 絶対に単離できないと主張しているのである。
加速器内での クォークなどの 間接的な測定によるものは ほんのわずかなもので そのほとんどは 無数のノイズにすぎず これは ヒッグス粒子と同じパターンである。
実際に 現在までに トップクォークは たったの 20 個ぐらいしか 加速器内で見つかっていない と彼らは言っている ( もちろん直接的な観測ではない )。
これらの間接的な観測は すべて 曖昧で不明瞭にも関わらず どうして 私達は これら想像上の粒子を リアリティー として受け入れなければならないのか?
(Fig.3) "時間のギャップ" が 想像上の粒子を生み出した。

このページで示したように、これらのねじれた状況は 難解な3体問題と コンピューターに関連した "時間のギャップ" ( 1920年代 - 1990年代 ) によって生じたと言っていい。
これらは 量子もつれ、量子コンピューター、ブラックホール、ひも理論などの 非実在の概念を受け入れなければならない 理由と同じ原理である。
残念ながら もし これら分数電荷や ヒッグス粒子を "リアリティー" として受け入れるとしたら、あなた方の前には 10 次元のひも理論 ( もしくは 11 次元の M 理論 ) しか残っていない。
最初に このページに示したように、 特殊相対論が間違いであるという 実際の証明を 無視したら、これらの様々な 奇妙な幻想が生じるのは 当たり前の話である。
(Fig.3') "長い"歴史の結果 = "非実在" の ひも理論の勝利。

このページに示したように、ループ量子重力理論 (LQG) などの 他の重力理論は 量子力学と相対論の統一に 失敗した。
そのため 現在 非現実的な ひも理論しか 最終理論として残っておらず、実際見て分かるように ひも理論が物理界で支配的な立場を取っている。
もし LQG が 統一理論として成功できるとしたら、とっくの昔に すでに成功しているだろう。
しかし 現実には 成功していない。
つまり 40 年以上にもわたる 十分とも言える時間が経過し、 LQG などの他の重力理論を完全に駆逐したのである。
LQG は 現実の3次元空間を 1次元のループに置き換えてしまったが、これは ある意味 違った意味での 異次元世界と言える。
(Fig.4) 多世界解釈だめ。ガイド波理論だめ。 → 永遠に "Shut up !" = 科学?
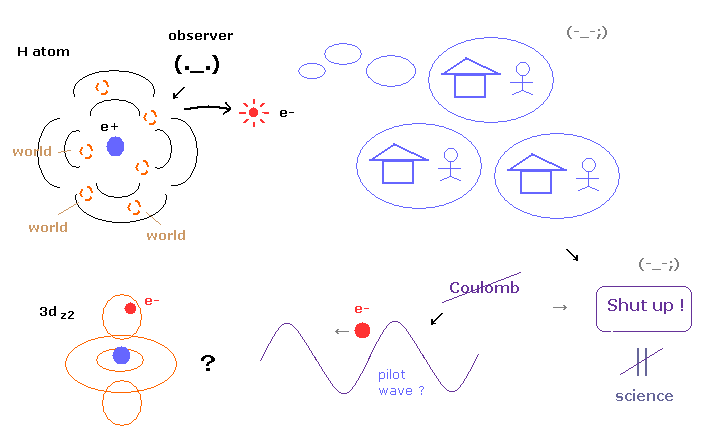
このページに示したように、 多世界解釈 (= 現在のところトップの座 ) は 非常に非現実的で、一方 ガイド波理論 (= ボーム解釈 ) は クーロンの法則に 従わず また ガイド波と粒子間の力学的関係が 不明瞭である。
このようにすべての解釈は 非常に不自然で 致命的な欠陥を含んでいるため ほぼすべての物理学者達は 単に "Shut up and calculate !" を貫き、要するに 何かと問うこと自体を 諦めているのが現状である。
実際に 量子力学の波束の収束の解釈に関する議論は エンドレスで終わりがない。
例え この議論を 永遠に続けても はっきり言って 何の進展もない。
しかし 本来 "科学" というのは 私達の目前に 何か未知のものがあるなら それに関して とことん問いただす のが基本である。
あなた方も感じられると思うが "問うのを諦める" (= "Shut up and caluculate !" ) ことは 科学の基本的姿勢に 完全に反している行為である。
(Fig.5) 現在の量子力学は いつ、どこで おかしくなってしまったのか?
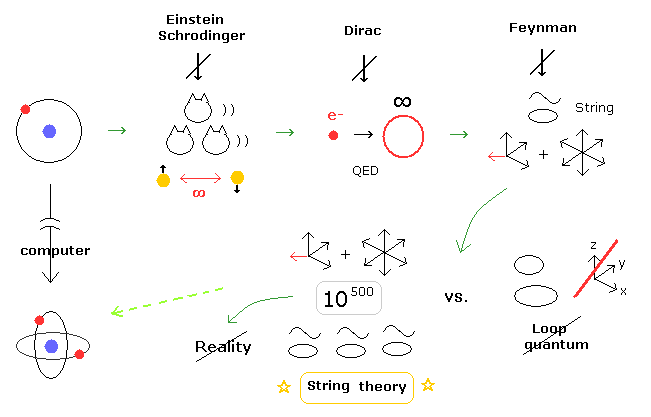
あなた方も感じていると思うが、多世界解釈 (= シュレディンガーの猫 )、超光速の量子もつれ、QED の無限大、クォークの分数電荷、10 次元のひも理論は すべて理不尽で 非現実的である。
このページに示したように、これらの深刻な問題は 1920 年代の 3体問題のヘリウムと コンピューターという装置がなかったことに起因していると言っていい。
もちろん、ボーア模型の初期物理の戻ることは 現在の物理に多大な影響を与えるため、彼らが ここまでの大きな変化を望まないことは十分に理解できる。
しかし 現在の量子力学的世界が あまりにも理不尽で 非現実的にも関わらず なぜ そのままの状態で受け入れられてきたのかという 奇妙な理由の つじつまの合った説明が ボーア模型を考えると ぴったり できてしまうのである。
(Fig.6) これらの架空の概念は "永遠に" 役に立たない。
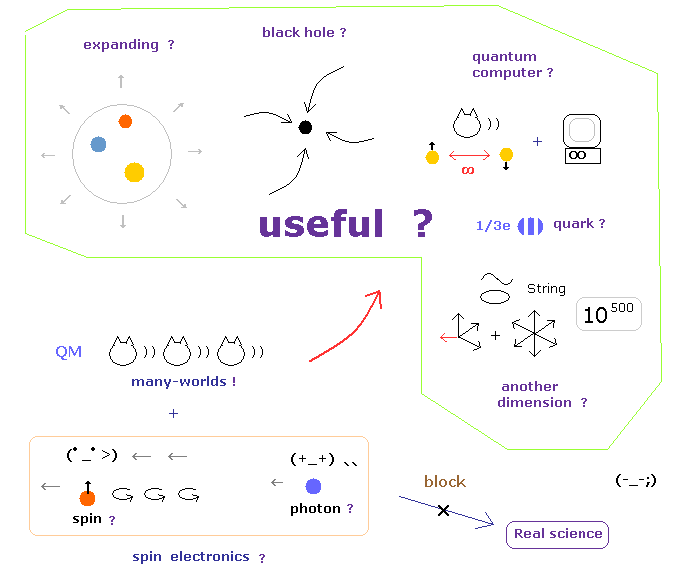
例えば、ヒッグス発見のセンセーショナルなニュースを聞いたとき、私達は 今一度 これらの粒子が 本当に 日々の生活に 役に立つのか 冷静に見つめ直す必要がある。
無数のヒッグス粒子とエーテルの違いについて質問しても、彼らはただ 「 ヒッグス粒子は ヒッグス場やエーテルとは異なる。」というフレーズを繰り返して 基本的な姿勢は " Shut up ! " である。
そして 加速器内の無数のノイズに埋もれた現象を何かに利用しようとしても、非現実的で 相対論に反する 仮想粒子の存在のせいで それが阻害されてしまう。
また 現在の 不気味なリンクや 量子もつれに関する研究や ジャーナルなどは 明らかに 非現実的な世界を 物理の勝利のごとく 書きたて、非実在のものを追及することを正当化してしまっている。
お気づきだと思われるが、非現実的な世界を目指すということは これらのものが 永遠に 私達の生活に役に立たないことを意味している。
なぜなら、"非実在"のものだからである。
(Fig.7) プログラム実行直後の画面 ( C-C )。

このページで、 C-C 結合長が実験値 (= 1.5352 Å ) のとき、両方の炭素原子核が 安定になることを 古典的な軌道と 下のプログラムを用いて説明することができた。
サンプル JAVA プログラム, or
サンプルプログラム (text).
このテキストエディタを "twoato.java" としてセーブしてコンパイルしてほしい。 "-Xlint : unchecked ---" などの注意は無視して実行できる。
ここでは 1 MM = 10-14 meter の新しい単位を使用している。
(Fig.8) C-C 結合長が実験値 = 1.5351 Å。

C-C の核間距離が 実験値 (= 1.5351 Å ) のとき、A と B 原子核に作用する力の x 成分 (FX) は ほぼ同じ -340 と -341 になり、これは 安定した核間距離を意味している。
炭素の電子は 軌道運動しており、A と B の状態を繰り返して ( フリップ ) しているため、-340 と -341 の違いは ほぼゼロになり、 安定になる。
この結果は クーロンとドブロイの関係が 実際の C-C 結合においても有効であることを示している。
| C-C (MM) | A 核の FX | B 核の FX | それらの差 |
|---|---|---|---|
| 12000 | -856 | -1703 | -847 |
| 13000 | -633 | -1013 | -380 |
| 14000 | -479 | -627 | -148 |
| 15000 | -370 | -399 | -29 |
| 15351 | -340 | -341 | -1 ← |
| 16000 | -292 | -258 | +34 |
| 17000 | -234 | -168 | +66 |
| 18000 | -191 | -109 | +82 |
| 19000 | -158 | -69 | +89 |
Table 1 は C-C 結合長が 実験値 (= 15351 MM ) よりも短くなると、 "e0" 電子の 引力が強くなりすぎる。
一方で C-C 結合長が長くなると、両原子核間の反発力が優勢になる。
(Fig.9) 力 = 1000.
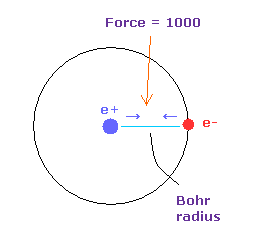
力の単位を Fig.9 に示した。
水素原子核の 電子と原子核間の力を "1000" とする。
そのため 電子と +e の原子核間の距離が ボーア半径のとき、その力は 1000 になる。
例えば 力 1468 は H 原子の基底状態の力の 1.468 倍ということになる。
ビリアル定理によれば、フリーの 2つの炭素原子のポテンシャルエネルギーは -148.025 × 4 = -592.1 eV (= フリー ).
( ここで 148.025 eV は 炭素の 1-4 のすべての価電子をイオン化するのに必要な全エネルギーである。 )
つまり Fig.7 の結合エネルギーは ( 596.7 (= tV ) - 592.1 ) × 0.5 = 2.3 eV となり、これは 実験値 3.5 eV (= 346 kl/mol ) に近い。
周囲の原子核の引力を考慮して 炭素の電子軌道を少し縮ませると、正確な 3.5eV の結合エネルギーを得ることができる。
なぜなら 誤差 1.4 eV の値は 炭素の 1-4 電子の全イオン化エネルギー (= 148.025 eV ) と比べて非常に小さいからである。
( もちろん、周囲の原子核の 正四面体の配置のために、炭素の4つの電子は ほぼ釣り合っている。)
ここでは このページで紹介した 2原子間において 炭素の価電子に働く力を 様々な異なる結合間で比較する。
このプログラム ( もしくは そのテキスト ) を実行後、 "C" (= 炭素 ) を "A atom" として選択する。
そして 様々な原子を "B atom" として選択して、それらの 炭素の電子 "ele 0" に対する影響について調べる。
(Fig.10) 炭素 の電子に作用する力の比較。
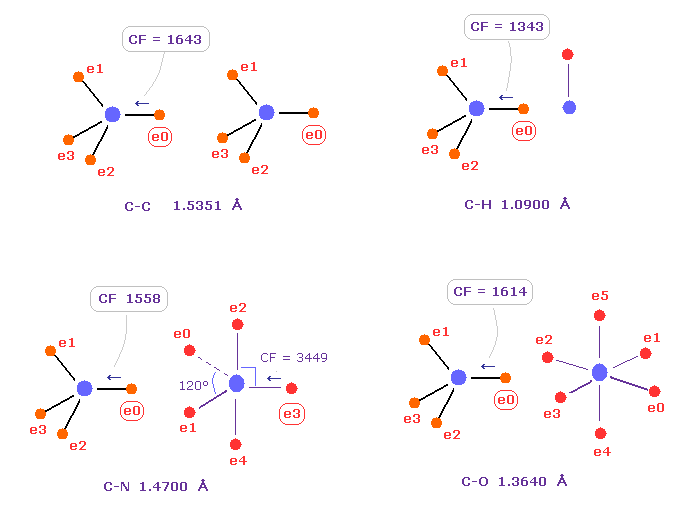
Fig.10 は C-C、 C-H、 C-N、 C-O のシングル結合における 力 CFを示したものである。
炭素が 様々な結合において 正四面体構造を 保っていることを考慮すると、炭素の電子に作用する力が 互いに ほぼ 等しくなるのが自然である。
実際に これらの力 (= CF ) は 異なった C-C、C-H、C-N、C-O 結合において それぞれ 1643, 1343, 1558, 1614 になる。
( これらの結合長は 実験値である、C-O の シングル結合は 酢酸からのものである。 )
| 分子結合 | その結合長 | 電子 e0 への力 |
|---|---|---|
| C - H | 1.0900 Å | CF = 1343 |
| C - C | 1.5351 Å | CF = 1643 |
| C - N | 1.4700 Å | CF = 1558 |
| C - O | 1.3640 Å | CF = 1614 |
| C - F | 1.3500 Å | CF = 1605 |
| C - Si | 1.8500 Å | CF = 1602 |
| C - P | 1.8400 Å | CF = 1584 |
| C - S | 1.8200 Å | CF = 1708 |
| C - Cl | 1.7700 Å | CF = 1626 |
Table 2 は 様々な結合における 炭素の電子 "ele 0" に作用する力 (= CF ) を示したものである。
驚くべきことに、異なった結合において、これらの力 (= CF ) は ほぼ 同じになる。
これはつまり 共通のメカニズムが働いて、炭素の正四面体の構造が 様々な結合において 保たれていることを示している。
Fig.10 の価電子 "e0" は 他の原子核に最も近づくため、この電子は 他の原子核の影響を最も受ける。
これはつまり この価電子の安定性が 結合長を決定する際の 重要なファクターの1つであることを意味している。
(Fig.11) 非現実的な量子化学は 原子核や電子の安定性について考慮していない。

量子力学 (化学) では、各電子は 非常に曖昧な存在で 無限大に広がっている。
Fig.7 の古典的軌道では、C-C 原子核間で 電子同士が避け合うことを考えて 簡単に 結合エネルギーを得ることができる。
しかし もちろんのことだが、量子化学では この非常に簡単な方法は 使えない。
彼らは 互いに避け合う電子を表すのに 非常に難解な数学上の行列式を "必ず" 使用しなければならない。
なぜなら 行列式において 2つの電子は同じ位置に入れないからである。
彼らは 元のパウリの排他原理を かなり拡大解釈して これらの反発する電子を表そうとしている。
(Fig.12) 基底関数の選択が 量子化学にとって最も重要である。
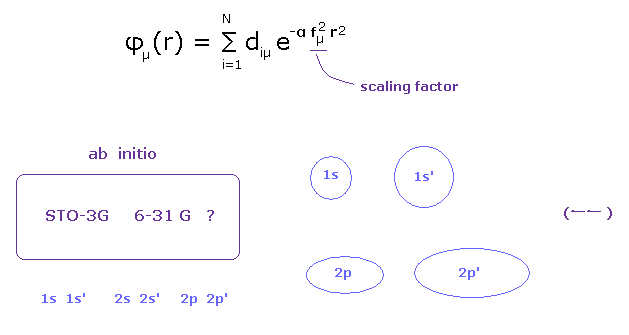
これら波動関数の非現実的な概念のために、量子化学は 非常に重要な概念である 原子核や価電子の安定性について考えることができない。
それは ただ "エネルギー" を見ることしかできない。
しかし その結合エネルギーというのは 原子のイオン化エネルギーに比して かなり小さい。
( 例えば C-C 結合では、 3.5 eV が 結合エネルギー、 296.05 eV = 2 × が炭素の 1-4 イオン化エネルギーである。 )
そのため 基底関数形の 人為的な選択によって これらの非常に小さな結合エネルギーを 容易に 操作することができる。
原子核と価電子そのものの安定性が より重要で かつ 結合長や結合角を決定するさいの主要な要因であると考えるのが自然である。
( このページも参照のこと。)
(Fig.12') 整数倍のドブロイ波長が 量子化学では保たれている。

ご存じのとおり、シュレディンガーの波動関数は ボーア模型と 完全に同じエネルギー準位を与えることができる。
これはつまり シュレディンガーの波動関数は 根本的に 同じ 整数倍のドブロイ波長に頼っているのである。 ( このページも参照のこと。 )
シュレディンガーの波動関数の指数関数部分の 電荷 Zの部分を変化させると、整数倍のドブロイ波長を保ったまま 軌道形を 自由に変更することができる。
このページに示したように、波動関数の 電荷部分が その場所における真の電荷に等しいとき、ビリアル定理により ポテンシャルエネルギーは 最も低くなる。
Fig.12'にあるように、もし 軌道形を自由に変更 ( ドブロイ波長を保って ) できたとしたら、
それらのポテンシャルエネルギーは ある制限 (= 整数倍のドブロイ波長 ) の条件のもとで 自由に 操作することが可能である。
量子化学は リアルな電子運動を考えることが できないため ただ エネルギーを見ることしかできない。
結果的に 軌道形を変えることによって 人為的にポテンシャルエネルギーを操作することができる。
(Fig.13) H2 分子。
このページでは、ボーア軌道を用いて 水素分子を表すのに成功した。
実際に A と B の原子核両方の 安定性 ( それに働く力 FX = 0 ) と 平均のドブロイ波長が "1.0000" ( ave = 1.0000 ) を考慮すると、H2 結合長の 本当の意味を説明することができた。
( このプログラムを用いる。)
| 核間距離 (MM) | A-X (MM) | A-Z (MM) | B-X (MM) | B-Z (MM) | 核への力 | ドブロイ波平均 | total V (eV) | 結合エネルギー |
|---|---|---|---|---|---|---|---|---|
| 6000 | 1870 | 4972 | -1870 | -4972 | 0 | 1.0000 | -60.664 | 3.120 |
| 6500 | 1145 | 4827 | -1145 | -4827 | 0 | 1.0000 | -62.204 | 3.890 |
| 7000 | 830 | 4755 | -830 | -4755 | 0 | 1.0000 | -62.893 | 4.234 |
| 7200 | 745 | 4739 | -745 | -4739 | 0 | 1.0000 | -63.014 | 4.295 |
| 7414 | 669 | 4729 | -669 | -4729 | 0 | 1.0000 | -63.056 | 4.316 |
| 7600 | 610 | 4724 | -610 | -4724 | 0 | 1.0000 | -63.047 | 4.311 |
| 7800 | 560 | 4721 | -560 | -4721 | 0 | 1.0000 | -63.010 | 4.293 |
| 8000 | 518 | 4720 | -518 | -4720 | 0 | 1.0000 | -62.952 | 4.264 |
| 9000 | 360 | 4741 | -360 | -4741 | 0 | 1.0000 | -62.365 | 3.971 |
Table 3 に示すように、H2 分子の結合長が 実験値 0.7414 Å (= 7414 MM ) のとき、 total V は もっとも低くなり、結合エネルギーは 最も高く (= 4.316 eV ) なり これは いい値である。
この結果は H2 結合長が 0.7414 Å であることが 古典力学的観点から明らかに説明できたことを示している。
水素のイオン化エネルギー (= 13.606 eV ) は H2 の結合エネルギーと比べて そんなに大きくない。
そのため この結合エネルギーを考慮することは 非常に重要である。
H2 結合エネルギーのみならず 原子核と電子の安定性に関しても 古典的軌道を用いて説明することができた。
量子化学では、 r12 (= 2つの電子間の距離 ) を含む関数を使用して これら電子間距離を 操作する必要がある。
なぜなら 電子間の反発を表すのに 行列式のみでは 限界があるからである。
(Fig.14) C=C の2重結合?
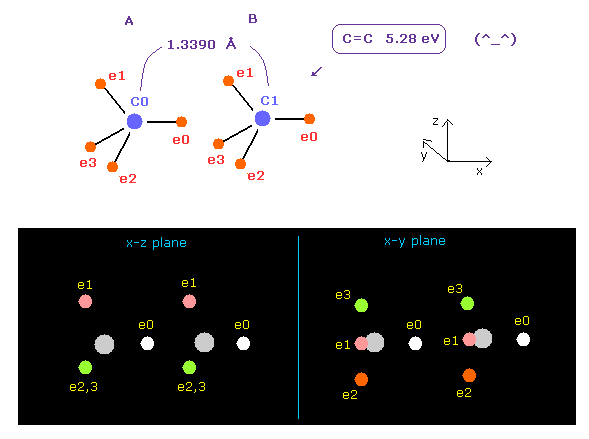
上記のプログラムを実行後、 "13390" を入力して "internuc" ボタンをクリックする。
C=C 2重結合の実験値は 1.3390 Å (= 結合長 ) と 602 kJ/mol (= 6.24 eV ) である。
Fig.14 のケースでは、 全ポテンシャルエネルギーは -602.652 eV となり、結合エネルギーは ( 602.652 - 592.1 (= フリーの C,C ) ) / 2 = 5.27 eV となり、この値は 実験値とほぼ同じである。
( この小さな違いは 炭素の電子軌道のいくらかを わずかに収縮させるとなくせる。)
しかし Fig.14 のケースでは、各炭素原子に作用する力は FX=-566、 FX=-836 となり、これは 互いに引きつけすぎていることを意味している。
(Fig.15) エチレンの結合長と結合角。
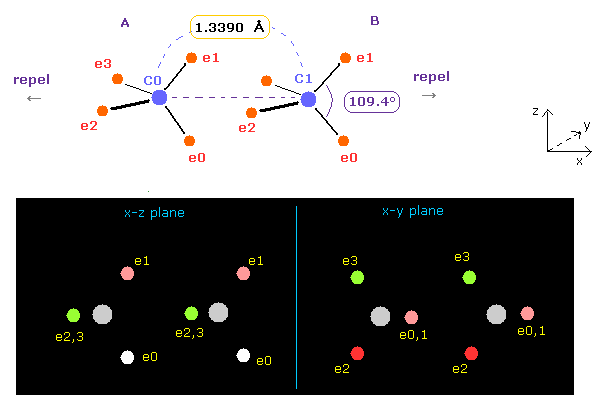
A と B の両原子を x-z 平面上で -54.7°回転させる。
( -54.7 をテキストボックス内に入力して "x-z ang" ボタンをクリックする。 このページも参照のこと。)
この状態では、ele 0,1 は z 軸に平行になり、 ele 2,3 は y 軸に平行になる。
このケースでは 両炭素原子核は 互いに 力 FX = 359 で 反発し合うことになる。
(Fig.16) エチレンにおける結合角と結合長。

Fig.15 では、炭素の価電子間の角度は 元の 109.4°のままである。
そこで 炭素 A の e2-n2-e3 の角度と、炭素 B の e0-n-e1 の角度を 117° (= H-C-H 角の実験値 ) に広げる。
Table 4 のように、 "3324" と "5487" を 指定のテキストボックス内に入力して エンターキーを押す。
そうすると、2つの炭素原子核間の反発力は ゼロになって 安定になる。
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | Waves |
|---|---|---|---|---|---|---|
| A ele 0 | 3706 | 0 | -5235 | 6414 | 2162 | 1.976 |
| - ele 1 | 3700 | 0 | 5239 | 6413 | 2162 | 1.976 |
| - ele 2 | -3324 | -5487 | 0 | 6415 | 2272 | 2.023 |
| - ele 3 | -3324 | 5487 | 0 | 6415 | 2272 | 2.023 |
| B ele 0 | 3324 | 0 | -5487 | 6415 | 2272 | 2.023 |
| - ele 1 | 3324 | 0 | 5487 | 6415 | 2272 | 2.023 |
| - ele 2 | -3703 | -5237 | 0 | 6413 | 2162 | 1.976 |
| - ele 3 | -3703 | 5237 | 0 | 6413 | 2162 | 1.976 |
| internuc (MM) | A nuc FX | B nuc FX | total V (eV) | A e2-n-e3 | B e0-n-e1 |
|---|---|---|---|---|---|
| C=C 13390 | 0 | 0 | -594.36 | 117 deg | 117 deg |
Table 4 に 示すように、A 原子の e2-nuc-3、B 原子の e0-nuc-e1 の角度が ちょうど 117° (= 実験値 ) のとき、 各原子核に作用する力 (= FX ) は ちょうど ゼロになる。
これはつまり C=C 結合の 2つの原子核は 安定になることを意味している。
C=C 結合における反発力は C-C よりも強い。そのため 外側の価電子間の角は 少し広くなる必要がある。
問題は Fig.16 の状態では、結合エネルギーが 1.7 eV だけになるということである。
(Fig.17) C=C 結合における 2つの状態間の振動。

Fig.14 の適切な結合エネルギーと Fig.16 の安定な原子核とを考慮すると、C=C の2つの炭素は Fig.17 の異なった状態間を 振動していると考えられる。
Fig.17 の 複合運動が C=C 2重結合の 真の状態である。 ( つまり そんなに単純ではない。 )
Fig.17 の上のケースでは、 炭素の電子は 外側の 2つの水素に引きつけられている。
下のケースでは、それらは もう一方の炭素原子核に引きつけられている。
もちろん、Fig.16 のケースにおいても 運動エネルギーの減少や C=C 間の4つの電子の引きつけなどにより 結合エネルギーが保たれると考えられる。
(Fig.18) C = C ( π ) 結合はリアルなのか ?

エチレンの4つの水素原子は 同一平面上にある。
量子化学では これは 2つの 2p 軌道がペアを形成し π結合となるためだと主張している。
しかし この説明はおかしいと言わざるを得ない。なぜなら 2つの負の電子は 互いに避け合うのが自然だからである。
それに基本的に 上で説明したとおり、各電子が 同一方向を向いているとき、実験値の結合エネルギーに到達できない。
基本的なクーロン力に逆らう この理不尽で不思議な力は いったいぜんたい何なのかということである。
(Fig.19) "縮んだ" + "伸びた" 軌道のペアが安定である。

炭素の価電子は C 原子核周囲を運動している。
基本的に これらの電子は わずかに H もしくは C 原子核のほうへ 伸びている。
Fig.19 の上部では 縮んだ軌道 (= s ) と 伸びた軌道 (= e ) が C=C 原子核間で 向き合っている。
( つまり 1方は 伸びて、他方は避けている。)
しかし FIg.19 の下図では、両サイドの軌道が 伸びる ( "e" と "e" ) か、 両サイドが 縮んで ( "s" と "s" ) いる。
そのため 結合状態は それらの ミスマッチのペアのために 上図より 少し 不安定になると考えられる。
この説明のほうが 奇妙な π結合よりも自然である。なぜなら 基本的なクーロン力に従っているからである。
(Fig.20) C ≡ C 3重結合。

アセチレンの C≡C 結合長は 1.2000 Å である。
上記のプログラムを実行後、 "12000" を入力して "internuc" ボタンをクリックする。
すると、 全ポテンシャルエネルギー (= tV ) は -612.634 eV になり、 結合エネルギーは ( 612.634 - 592.1 ) / 2 = 10.25 eV となる。これは 実験値 8.65 eV よりも少し大きい。
実際に 1.2000 Å の C≡C 結合長は 2 × 炭素 の 電子軌道半径 (= 2 × 0.6415 Å = 1.2830 Å ) よりも少し短い。
そのため "e0" 電子に作用する 力 CF は マイナス (= -489 ) になり、これはつまり A 原子の e0 電子が B 原子に引きつけられていることを示している。
もちろん これは変である。
炭素 B の 3つの価電子 ( e1 - e3 ) が C0 原子核に引きつけられて "e0" の電子を 反発していることを考慮する必要がある。
(Fig.21) C ≡ C 3重結合。

反発相互作用を考慮して、e0 電子を x-z 平面で 10°回転させると、実験値 (= 8.65 eV ) とほぼ同じ結合エネルギー (= 8.5 eV ) を得ることができる。
このケースでは 全ポテンシャルエネルギーが -609.187 eV であるため 結合エネルギーは ( 609.187 - 592.1 ) / 2 = 8.5 eV になる。
(Fig.22) C ≡ C 3重結合。正四面体構造が壊れる。

アセチレン ( HC≡CH ) では、2つの水素原子しかない。
そのため 各炭素の 3つの価電子は すべて他の炭素原子核へ近づいている。
つまり 炭素内部の 4つの電子間の反発力に打ち勝って 正四面体構造が 少し壊れて
しまう。
他の炭素の これら3つの電子 ( e1-e3 ) によって、C0 の e0 電子は 反発され、その元の軌道に戻ることができる。
もちろん、この壊れた正四面体の構造のために、 C≡C 結合は 容易に 2重もしくは 単結合に変わってしまう。
Fig.20 と Fig.21 では 電子 "e0" の安定性と 力 CF を考慮すれば、この 1.2000 Å の結合長が 下限であろうと考えられる。
(Fig.23) C-H 結合エネルギー = 4.0 eV。

平均の C-H 結合長は 1.0900 Å である。
上記のプログラムを実行した後、 "10900" を入力して "internuc" ボタンをクリックする。
その後、 C と H 原子を それぞれ A と B 原子として選ぶ。
"5200" (= 約 ボーア半径 ) を B 原子の "+Z (MM)" のテキストボックスに入れて、エンターキーを押す。
この状態では 全ポテンシャルエネルギー (= tV ) は -331.169 eV になる。
また フリーの炭素と水素のポテンシャルエネルギーは ビリアル定理より ( -148.025 (= 1-4 のイオン化 ) - 13.606 ) × 2 = -323.262 eV となる。
つまり 結合エネルギーは ( 331.169 - 323.262 ) / 2 = 3.95 eV となり、この値は 実験値 4.25 eV とほぼ同じである。
(Fig.24) C-H 結合長は安定である。

Fig.23 では、 e0 電子は 水素に近い。そのため 水素の電子は 反発され ボーア半径でも 良い結合エネルギーが得られた。
しかし 実際には 水素の軌道は 炭素の引力のために 少し 縮む。
"4750" を 水素の電子の +Z (MM) として選ぶと、平均のドブロイ波は ほぼ 1.0 になる。
このケースでは 炭素と水素原子核間の 平均の力は ほぼゼロ (= 9.5 ) になる。
なぜなら 炭素の原子核は 反発されるが 水素の原子核が e0 電子に引きつけられ、これが 反発力をキャンセルするからである。
結果的に C-C 結合長のように、C-H 結合長は 1.0900 Å のときに安定になる。
サンプル JAVA プログラム (= エタン。 )
サンプル JAVA プログラム (= エチレン。 )
これらは エタン と エチレン分子を視覚化する サンプル JAVA プログラムである。
これらのテキストは "etham.java" もしくは "ethylen.java" とセーブしてコンパイルしてほしい。
操作方法は このページと全く同じである。
これらのプログラムでは、原子をそのまま示しているだけで Fig.24 のような 電子運動の平均値は考慮していない。
そのため ゆくゆくは これらのプログラムを平均の電子運動を表すよう改変していくつもりである。
(Fig.25) N-H 結合における反発力。

平均の N-H 結合長は 1.0100 Å である。
上記のプログラムを実行後、 "10100" を入力して "internuc" ボタンをクリックする。
そして N と H 原子を A、 B 原子として選ぶ。
この状態では 全ポテンシャルエネルギー (= tV ) は -569.68 eV になる。
また フリーの窒素と水素のポテンシャルエネルギーは ビリアル定理を用いて ( -266.95 (= 1-5 イオン化 ) -13.606 ) × 2 = -561.11 eV となる。
つまり 結合エネルギーは ( 569.68 - 561.11 ) / 2 = 4.285 eV で、これは 実験値 4.00 eV と ほぼ 同じである。
( このケースでは、窒素の電子は 水素の電子に少し反発されている。)
また N-H 結合間の平均の反発力は Fig.25 に示したように 275 になる。
(Fig.26) C-N 結合における反発力。

平均の C-N 結合長は 1.4700 Å である。
上記のプログラムを実行後、 "14700" を入力し、"internuc" ボタンをクリックする。
C と N 原子を A、 B 原子として選ぶ。
この状態では、全ポテンシャルエネルギー (= tV ) は -834.84 eV になる。
また フリーの窒素と炭素のポテンシャルエネルギーは ビリアル定理を用いて ( -266.95 (= 1-5 イオン化 ) - 148.025 (= 1-4 イオン化 ) ) × 2 = -829.9 eV となる。
よって 結合エネルギーは ( 834.84 - 829.9 ) / 2 = 2.5 eV で これは 実験値 3.1 eV と ほぼ同じである。
( このケースでは、電子軌道は 核の引力によって 少し縮んでいる。)
また C-N 結合の平均の反発力は Fig.26 に示したように 88 になる。
(Fig.27) ペプチド結合における 力のバランス。

よって 基本的に N-H 結合の反発力 (= 275 ) は N-C 結合 (= 88.5 ) のよりも強い。
ペプチド結合は 同一平面上にあり、その C-N-C 角は 約 122°である。
Fig.25 と Fig.26 を用いて 力のバランスを考慮して、N の価電子の角度を 120°から 122°に少し広げる。
このケースでは N 原子核に作用する力は 36 になり、これは ほぼゼロで 安定ということになる。
基本的に、N-H 結合における 強い"押す"力によって アンモニア (NH3) は ねじれて 同一平面上になれない。
(Fig.28) H2SO4 の Pubchem 3D SDF 分子構造。

このセクションでは NIH の Pubchem 3D 分子構造データを利用する。このサイトは 低分子のデータの いいソースである。
Pubchem のサイトを見て、"sulfuric acid" のワードで検索する。
sulfuric acid のサイトを表示した後、 右上の "3D: SDF: Display" のところをクリックする。
Fig.28 のデータが 画面に表示される。そこで 青線で囲まれた部分を テキストエディタに コピー & ペーストする。
そして このテキストファイルを どこかのフォルダにセーブする。
(Fig.29) H2SO4 の 3D 座標と 隣同士の原子情報。

基本的に Fig.29 の 上部は 各原子の x、y、z 座標 ( Å ) を示している。
そして Fig.29 の下部は 隣り合った原子番号の情報を示している。
例えば、atom 1 (= S ) の 隣りの原子は 2 (= O )、 3 (= O )、 4 (= O, double )、 5 (= O, double ) ということになる。
Sample JAVA program ( pubchem data 利用。 )
(Fig.30) プログラム内の フォルダー名の変更。

このテキストエディタを どこか違うフォルダにセーブしたときは、上記プログラム内の その場所の部分を変更するように。
( Fig.30 の青線部分を変更する。 )
(Fig.31) H2SO4 の分子構造。

このプログラムを実行後、Fig.31 の絵が 画面上に表示される。
操作方法は このページとまったく同じである。
(Fig.32) H2SO4 の安定性。

H2SO4 の 中心の硫黄に作用する力の成分を見ると、それは ほぼゼロである。
つまり 硫黄 S は 安定状態ということになる。
Pubchem のデータは CRC の構造データとは少し異なるが だいたい同じである。
上記のプログラムでは 各原子の 電子の先端が 低番号の原子の方を 初期化時に向くように設定してある。
様々な結合状態を表すには、その向きや配置を少し変えていく必要がある。一度試してみてほしい。
(Fig.33) S=O の結合エネルギー。

平均の S=O の2重結合長は 1.4300 Å である。
上記のプログラムを実行後、"14300" を入力して "internuc" ボタンをクリックする。
それから S と O 原子を A、 B 原子として それぞれ選ぶ。
この状態では、全ポテンシャルエネルギー (= tV ) は -1428.064 eV となる。
フリーの硫黄と酸素原子のポテンシャルエネルギーは ビリアル定理を用いて ( -276.36 (= 1-6 イオン化 ) - 433.1 (= 1-6 イオン化 ) ) × 2 = -1418.9 eV となる。
つまり 結合エネルギーは ( 1428.064 - 1418.9 ) / 2 = 4.58 eV となり これは 実験値 5.41 eV と ほぼ同じである。
( つまり このケースでは 電子軌道は 核の引力のため 少し縮んでいる。)
次に pubchem data を用いて 硝酸 (= HNO3 ) について調べることにする。
Fig.29 のように、pubchem から 次の構造データを得る。
このテキストを "C:\sdff" のフォルダに "nitric-acid.text" というファイル名でセーブする。
(Fig.34) プログラム内のアドレス変更。

Fi.34 のように 上記プログラム内のアドレスを変更する。
ここでは このプログラムを使用する。
このプログラムを "sdfd2.java" としてセーブしてコンパイルする。
(Fig.35) N 原子核の力のバランス。

上記プログラム実行後、 "3" (= 窒素 ) をテキストボックス内に入力して "top nucl" ( もしくは "nucleus" ) ボタンをクリックする。
硝酸の全原子が ほぼ同一平面上 (= x-y 平面 ) にあることがわかる。
Fig.35 に見られるように、N 原子核に作用する トータルの力は ほぼ 釣り合っている。
力 FY (= 150 ) は 他の力の成分よりも わずかに大きい。
窒素の2つの価電子の角度を少し広げると ( なぜなら 131° は 120°より少し広い ) この力 FY は キャンセルできる。
初期化時に、酸素の電子は 窒素の方向を向いている。
よって それらの間の反発力を避けるため 各酸素の電子を 45°回転する。
すると N 原子は より安定になる。試してみるといい。

2013/5/21 updated This site is link free.