トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは幻想である。
トップページでは、3体系である ヘリウム原子の換算質量を計算した。
質量中心がヘリウム原子の位置にある場合を除いて この換算質量を用いることで、 量子力学的な変分法よりも正確な 結果を得ることができた。
(Fig.1)

最初に、2体問題の水素原子について説明する。
なぜなら ヘリウムの換算質量はこの水素原子をベースにして計算しているからである。
粒子1を水素の原子核、粒子2を電子とする。
まず、次のように定義する。
(Eq.1)
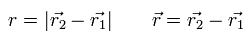
ここでは r1 と r2 は 各粒子の 位置ベクトル を意味している。
2つの粒子間の力が f(r) のとき、粒子1の 運動方程式は 次のようになる。
(Eq.2)
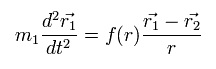
ここでは m1 は 粒子 1 の質量を表している。
また、粒子2は次の方程式を満たす。
(Eq.3)
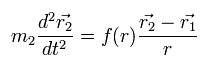
これらの関係式は 作用・反作用の法則を満足している。
Eq.2 を Eq.3 から 差し引くと、次の式が得られる。
(Eq.4)
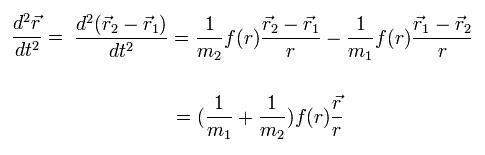
ここでは、 Eq.1 の関係も使っている。
ここで 次の換算質量 (μ) を使う。
(Eq.5)
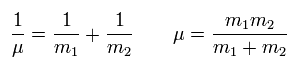
すると、Eq.4 は次のように表せる。
(Eq.6)
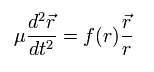
Eq.6 は、もし 原子核のみ静止していると見なそうとすると、 換算質量 (μ) を使う必要があることを意味している。
さらに換算質量が有効であるには、原子核の運動エネルギーが 換算質量をもつ軽い粒子のほうに吸収されているかを確認する必要がある。
系の質量中心 (R) の座標は、
(Eq.7)
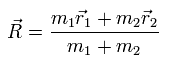
Eq.1 と Eq.7 より、
(Eq.8)
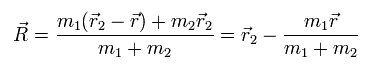
同じように、次を得る。
(Eq.9)
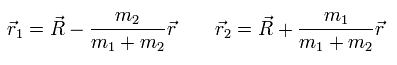
よって、2つの粒子の全運動エネルギーは
(Eq.10)
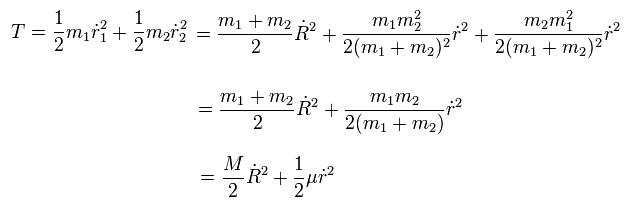
Eq.10 に示すように、全運動エネルギーは 質量中心の運動と 2つの粒子間の相対運動の和になっている。
Eq.6 と Eq.10 から、換算質量を使用することは、力とエネルギーの両面からみて、原子核を静止していると見なせることを示している。
(Eq.11) 換算質量と速度の関係。
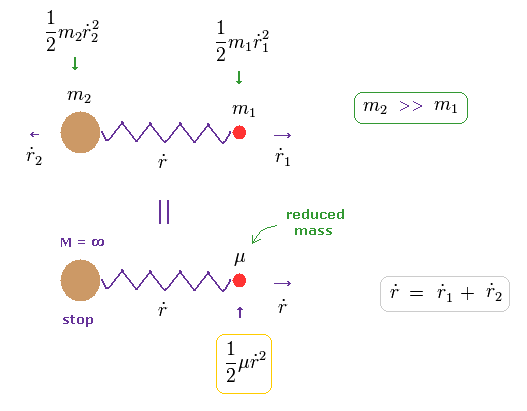
Eq.10 で、質量中心 (= R ) の速度が ゼロのとき、全運動エネルギーは 換算質量 (= μ ) と 相対速度 (= dot r ) のみ で表される。
( Eq.11 では、 m2 と m1 が 逆方向の運動のため 全運動量がゼロ である。 )
Eq.11 の下では μ の質量のみが 1方向へ動いているため 全運動量がゼロになっていないように見える。
実は 換算実量 μ が使用された瞬間に 重い m2 の質量は 自動的に 無限大になるからである。
つまり この無限大の質量 × 速度2 (= 0 ) は ゼロにならないのである。
よって μ と m2 の 全運動量は保存される。
3体問題であるヘリウム原子の場合は、少し複雑である。
このページも参照のこと。
(Fig.2) 水素とヘリウムの原子核。
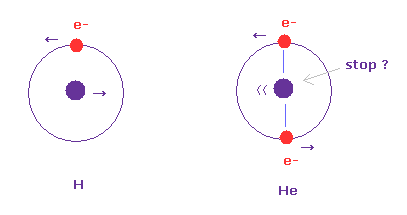
水素原子のケース (= Fig.2 左 ) では、 原子核は 2体問題のために 必ず動いている。
しかし Fig.2 右 ( 2つの電子が 原子核のちょうど真反対 ) では、そのヘリウム原子核は 静止している。なぜなら それが 2つの電子に挟まれたちょうど平衡地点にあるからである。
もちろん Fig.2 右の ヘリウム模型は 実際の基底状態のエネルギーとは 少し異なった値になることが 知られている。
では 2つの電子軌道が 互いに 垂直のときは どうであろうか?
( 量子力学の 曖昧な波動関数は これらの違いを 見分けられない。このことも 量子力学が間違いであることの 理由の1つである。 )
(Fig.3) 原子核が 回転でなく 直線状の振動運動 をしている (= 特殊例 )。
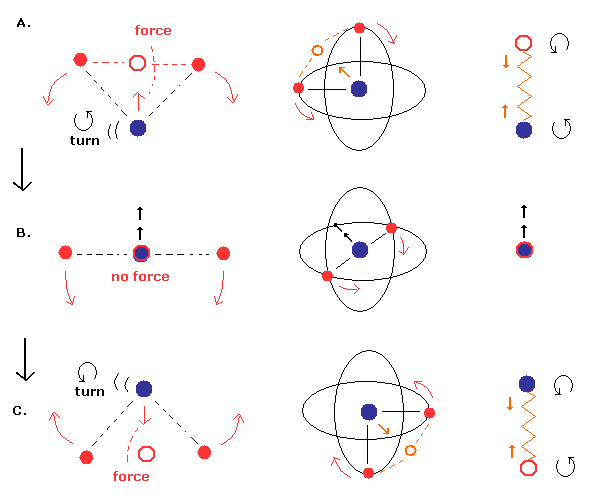
最初に、原子核と2つの電子が バネのように振動しているケースを考える。
Fig.8 (= ノーマルパターン ) と異なり、原子核の速度 (回転ではなく) は 重心が原子核のところにあるときに 最大になる (Fig.3B)。
そして Fig.3A と Fig.3C において、原子核の 向きが変わる。そのため その地点で 原子核の速度がゼロになる。
サンプル JAVA プログラム (= 原子核が Fig.3 のように振動している。)
サンプル C 言語 プログラム
下のソースプログラムをそのままテキストエディタ(メモ帳など)にコピー and ペースト すれば、簡単にコンパイルと実行できる。
このプログラムでは、最初に 電子1の初期の y座標 r2 (MM) (Fig.4 参照) と ヘリウム の全エネルギー E の絶対値 (eV) を入力する。
それらを入力すると、電子が、1/4 周した後の Fig.5 における電子1の速度の x成分 と、軌道 1/4 周に含まれるド・ブロイ波の数 ( midWN ) が画面に表示される。
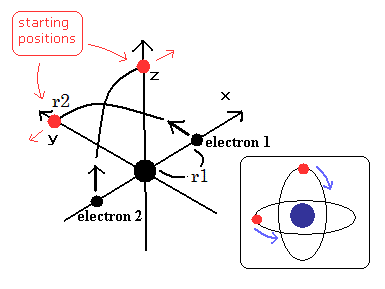
(Fig.4) Fig.3 モデルの スタート地点。.
(Fig.5) 電子が 1/4 周した地点。
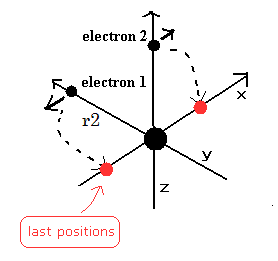
Fig.4 の地点をスタート地点に選ぶ。
なぜなら Fig.3 の運動パターンでは、電子が Fig.3A と 3C の地点にあるとき ヘリウム原子核がストップするからである。
そのため Fig.4 の初期速度を計算するとき、換算質量でなく通常質量を使用する。
(スタート後は 換算質量を使う。)
Table 1 は Fig.3 の "原子核 振動モデル" の結果である。( last VX = 0 ).
| E (eV) | r2 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0000 | 3137.0 | 0.250011 | 1.000044 |
| -79.0037 | 3137.5 | 0.250005 | 1.000020 |
| -79.0069 | 3136.5 | 0.250000 | 1.000000 |
| -79.0100 | 3136.0 | 0.249996 | 0.999984 |
| -79.0300 | 3135.5 | 0.249964 | 0.999856 |
Table 1 に示すように、電子間の反発力のために r2 は r1 より少し長い。
また Table 4 の結果は -79.0069 eV で これは Table 1 の -79.0037 eV と少し違う。
( 実験値は -79.005 eV である。 )
もちろん この結果は 最新の量子力学的手法 (= -79.015 eV ) よりも正確である。
しかし Fig.3 (= Table 1 ) モデルでは 相対論的な補正値のみ説明することができない。
Fig.3 の 原子核振動モデルは 非常に "特殊"な場合であり、普通は起こりにくい。
例えば、互いに引き合う 惑星は 普通は 振動ではなく 回転する。
(Fig.6) スタート地点 = 換算質量でない。
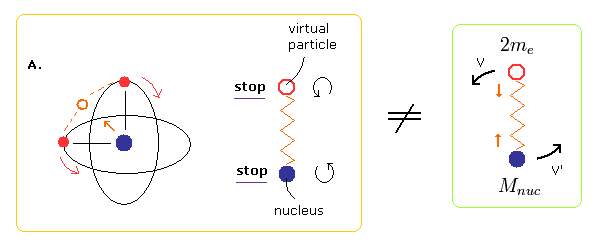
2体問題の水素原子と異なり、Fig.3 の振動運動は 原子核がストップする2つの地点を含んでいる (= Fig.3 の A と C )。
Fig.3 の A と C の地点では、2つの電子の中間の仮想粒子もストップしている。
そのため、Fig.3 の A をスタート地点として選ぶと、電子の初期速度の計算のとき 換算質量を使用してはいけない。
なぜなら、換算質量を使用することは 仮想粒子と原子核が 水素原子のように振る舞うことを意味しているからである。
しかし それらはストップしている。
(Fig.7) ヘリウム原子の換算質量。

Fig.3 の他の地点では 原子核と仮想粒子は (直線状に) 動いている。
また 仮想粒子が 原子核の運動に影響を与える唯一の存在とみなせる。
そのため このケースでは 換算質量を用いれば 原子核が止まっているように見なせる。
ヘリウムの電子の数は "2" であるため、各電子は 換算質量全体の半分になる。
(Eq.12)
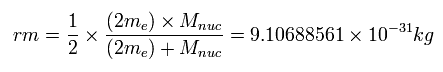
換算質量と通常質量のこれらの正確な区別により ヘリウムの基底状態の 正確で真の値を得ることができる。
(Fig.8) 原子核と仮想粒子が回転している。
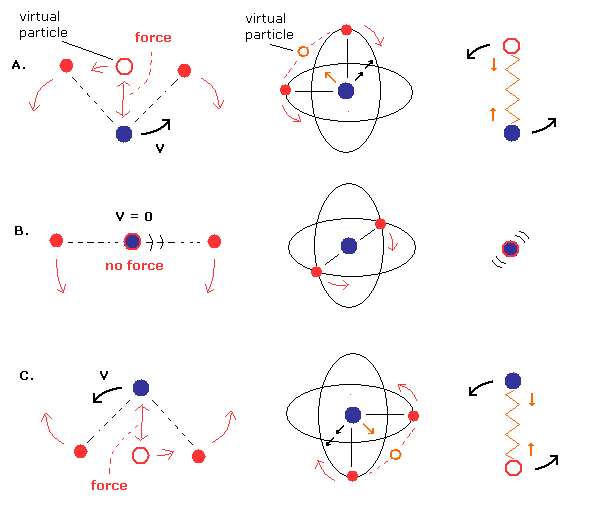
実際には ヘリウム原子の静止系でみて、2つの電子の間の仮想粒子が 原子核 (= 質量中心 ) の地点にあるとき、それらは 一時的にストップする (= Fig.8B, Fig.10 )。
なぜなら クーロン反発力を考慮すると Fig.8B と Fig.10 の状態が最も安定な平衡状態だからである。
(Fig.9) 質量中心では "接線方向"の速度のみが 残っている。
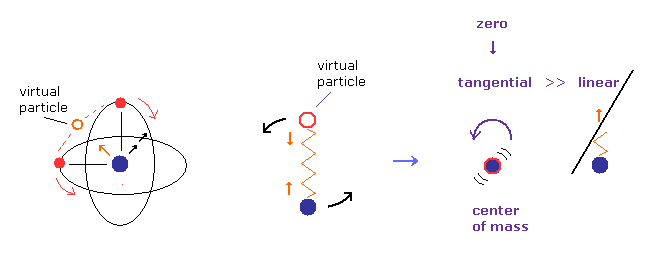
角運動量の保存則を考慮すると、Fig.8B において 原子核が 質量中心に近づくにつれて その 接線 (回転) 方向 の速度は 線状方向の速度よりも はるかに大きくなる。
( 回転するフィギアスケーターを思い浮かべると分かる。)
そのため 質量中心が原点にあるとき 原子核の線状運動を無視できる。
もちろん 回転半径がゼロになれば、接線方向の速度もゼロになる。
つまり Fig.8 模型を選択すると、2つの電子が 原子核のちょうど正反対にあるとき、換算質量でなく 通常の質量を用いる必要がある。
(Fig.10) 正反対が最も安定位置。
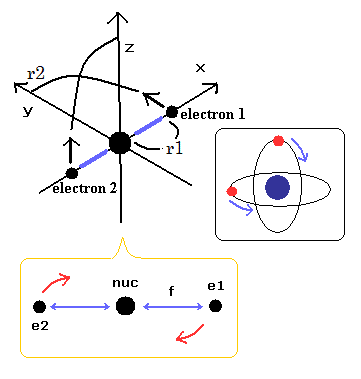
Fig.10 では、2つの電子が 原子核のちょうど反対位置にある。
しかし その状態の前後においては、ドブロイ波の干渉のために、2つの軌道は ちょうど互いに垂直になる必要がある。
( もしそれらが垂直でないと、それらのちょうど逆の波の位相がキャンセルしあって 不安定になる。)
この力は ドブロイ波の干渉によって生じ、もちろん 作用・反作用の法則 のために、原子核は ヘリウム内で 逆方向に押されることになる。
ポイントは 2つの電子の質量中心が原子核の位置にあるときが カーブの底のように 最も安定な状態だということである。
つまり この平衡地点 (= Fig.10 )のときのみ 原子核は止まり、電子の初期速度の計算のとき通常質量を使用する必要がある。
(Fig.11) 2つの電子が 1/4 周した時点。
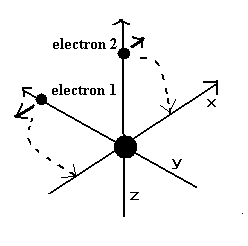
2つの電子が Fig.11 の方向へ動き出した瞬間に、その原子核は 質量中心からそれる。
そのため 原子核をストップさせるため、Eq.11 で説明したとおり、換算質量を用いる必要がある。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -78.9900 | 3075.0 | 0.250022 | 1.000088 |
| -79.0000 | 3074.0 | 0.250006 | 1.000024 |
| -79.0037 | 3074.0 | 0.250000 | 1.000000 |
| -79.0100 | 3074.0 | 0.249990 | 0.999960 |
| -79.0300 | 3073.0 | 0.249958 | 0.999832 |
この結果 (= -79.0037 eV ) は 実験値と ちょうど 一致している ( 相対論的補正を除いて )。
この結果は 明らかに Fig.8-Fig.11 のヘリウム模型が もっとも正確であることを示している。
次のプログラムを使用している。 詳細は このページも参照のこと。
このプログラムでは 電子の 通常質量もしくは 換算質量かを選択することができる。
サンプル JAVA プログラム 1 SS = 1 × 10-23
サンプル C 言語 プログラム
Table 3 は "Not reduced mass の条件" のときの結果である。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0037 | 3075.0 | 0.250071 | 1.000284 |
| -79.0300 | 3074.0 | 0.250030 | 1.000120 |
| -79.0485 | 3073.5 | 0.250000 | 1.000000 |
| -79.0600 | 3073.0 | 0.249982 | 0.999928 |
| -79.0800 | 3072.0 | 0.249950 | 0.999800 |
Table 3 に示したように、もし 中性ヘリウム原子において 換算質量を用いなかったら 計算結果は -79.0485 eV となり、 これは 実験結果 (-79.005147 eV) と異なる。
(誤差は -79.0485 - (-79.005147) = -0.04335 eV である。 Table 2 の結果の 0.001447 eV と比較するといい。)
もちろん この結果も 実験値とほぼ同じであることに変わりないが・・。
よって ヘリウムの正確な基底状態のエネルギーを得るには 換算質量を用いなければならないことを意味している。
Table 4 は "All reduced mass の条件" の結果である。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -79.0037 | 3075.0 | 0.250037 | 1.000148 |
| -79.0200 | 3074.5 | 0.250011 | 1.000044 |
| -79.0268 | 3074.0 | 0.250000 | 1.000000 |
| -79.0300 | 3074.0 | 0.249995 | 0.999980 |
| -79.0500 | 3073.0 | 0.249963 | 0.999852 |
Table 4 に示すように、重心が原子核の地点にあるときでさえ 換算質量を必ず使用したとすると、計算結果は -79.0268 eV となり、これは 実験結果 (-79.005147 eV) と異なる。
( ほぼ同じではあるが。)
つまり 最も正確な値を得るには それらの位置関係に応じて 換算質量か 通常質量を区別する必要がある。
(Fig.12) 電子が 原子核を押す (= 作用反作用の法則 )。
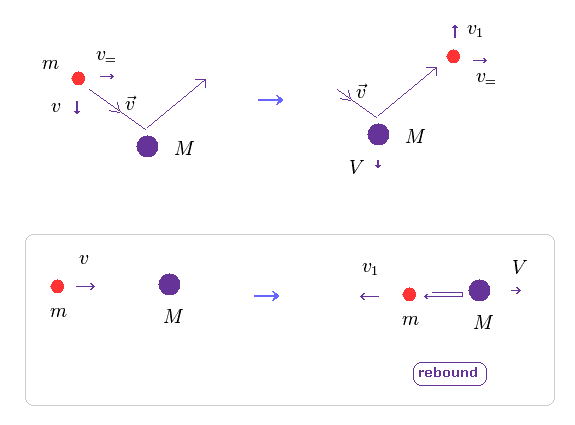
上で述べたように、2つの電子が 互いに垂直の方向に進んでいるとき、それらは ドブロイ波の干渉による影響を受ける。
もちろん、2つの電子中心が 系の質量中心を離れるとき、ヘリウム原子核は 作用反作用のため 電子に押される。
Fig.12 では、2つの粒子の衝突する方向 (= v, Fig.12 下 ) のみが重要である。
( 平行成分は変化しない。 )
(Eq.13) 全エネルギー保存。
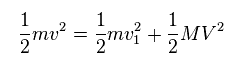
Eq.13 に示したように、この衝突の前後で、 全 ( 運動 ) エネルギーは 保存される。
Eq.13 では、 "m" は 電子の質量、 "M" は 原子核の質量である。
(Eq.14) 全運動量。
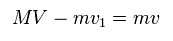
また 全運動量も保存される。
Eq.13 と Eq.14 から、次の各速度を得る。
(Eq.15) 各速度。
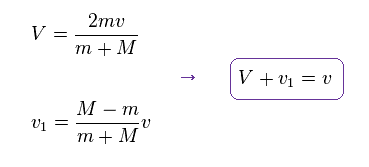
Eq.15 を Eq.13 と Eq.14 に代入して この結果を確かめることができる。
Eq.15 に示したように、Eq.11 の 相対速度は ほぼ保存される。
(Eq.16)
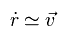
つまり Fig.10 で 通常の質量を用いて 最初の電子速度 (= v ) を得ると、その速度を 相対座標においても そのまま使用できる。
(Eq.17)
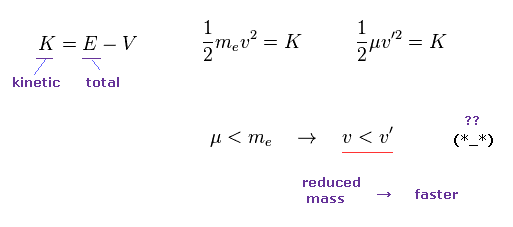
しかし 換算質量 (= μ ) から得られた初期速度を使用すると、この速度は 同じ運動エネルギー K の下で 速くなってしまう。
なぜなら 換算質量は 通常の質量よりも 小さいからである。
そのため もし 初期速度を 突然 換算質量を用いたものに変更すると、この電子は 突然速くなることになり、おかしな結果となってしまう。
つまり 通常質量から得られた初期速度をそのまま使用しなければならない。
初期の原子核速度のみが ゼロの条件は 全運動量保存がおかしくなるように見えるが それは違う。
Eq.11 に示したように 換算質量を使用した瞬間に 原子核質量が 無限大になるからである。

2013/9/30 updated This site is link free.