
トップページ (2電子原子も含む正確な新ボーア模型)
タンパク質の二面角の回転と操作
(Fig.1) 80 年以上が経過 → 波動関数は "謎" のまま = 役に立たない! なぜ ?

今年のノーベル化学賞は 計算化学分野に贈られた。
コンピューターを用いた計算化学は 実際の分子の動きを調べるのに 非常に重要であるため、この決定は 妥当といえる。
しかし 問題は この計算化学自体が 現在の化学者 (もちろん 生物学者 ) 達の間にほとんど浸透されておらず 人気が まったくないということである。
なぜなら 現在の計算化学は 波動関数 と パウリの排他原理を 未知な状態の 単なる数式として放置しているため 応用分野で まったく役立つことができないからである。
最も深刻な問題は すでに行き詰っているにも関わらず 彼らは これらの未知の波動関数とは何なのかを問おうとしないことにある。
計算を簡単にする方法を模索するのに 波動関数の意味自体を問い正すことは どう見ても必須事項である。
(Fig.2) 80 年以上が経過 → パウリの排他原理の力の源は不明のまま。 どうして?

スピンは それが回転だとすると スピンスピードが 光速の 100 倍以上 ( > 100 × c ) に達する必要があり、リアリティーが何もないに等しい。
また このページに示したように スピン磁気モーメントは パウリの排他原理を引き起こすには はっきり言って弱すぎる ( 微細構造レベルのスピンエネルギーが クーロン力と対等に 張り合うことは 不可能である。)
それでは いったい何が パウリの排他原理を引き起こす源なのだろうか?
スピン磁気モーメントが 弱すぎるとすると、この強力な力を引き起こせる存在は たった1つしか残っていない。
ドブロイ波 ( の干渉 ) が パウリの排他原理と強磁性 を引き起こす源と考えると しっくりくる。
( ヘリウム と このページを参照のこと。 )
非実在のスピン自体は ドブロイ波を生じさせることができないため、彼らは 単なる数学上の記号である反交換演算子にすべてを頼らざるを得なかった。
結果的に 私達が これらの反交換の意味を問うことができなくなり (= Shut up ! ) 、非常に不便な反対称の行列式 (= Fig.2 ) を使用するしか他に道がないのである。
(Fig.3) 物性物理学の DFT は 単なる "粗い" 近似にすぎない。

密度汎関数 (DFT) は 物性物理学の分野で よく使用される。
重要な点は DFT は 非常に重要な部分の 交換相関エネルギー (= Exc ) に関して 何も答えを出せない点である。
彼らは しばしば 局所密度近似 (LDA) という 一様な電子ガスを用いた 非常に粗い近似を使用する。
もちろん、現実の物質が 単純な一様状態でないことは明白であるため、実験値に合わせるために ある電荷勾配 (= GGA ) を人為的に付け加えたりする。
この GGA の いくつかのパラメーターは 実験値に合うように 人為的に調節しなければならない。
つまり DFT そのものは 第一原理ではない。
さらに DFT は タンパク質などの 弱い分子間力を扱うときには まったく役に立たない。
(Fig.4) 分子力学法には 電子という概念がない。

分子力学法 ( MM 法 ) や 分子動力学法 ( MD 法 ) は 分子間相互作用を 古典力学的に考え直したものである。
複雑すぎて役に立たない量子力学の波動関数のために、大きな分子では この分子力学法が
量子化学の代わりに用いられている。
MM 法では 結合長や結合角などが 古典的な "バネ" のように扱われている。
最も重要な問題は MM 法には 電子という 概念が ないということである。
つまり これらの古典的な電位は 経験的 (= 第一原理ではなく ) に決める必要がある。
しかし例えば アミノ酸は 20 種類存在するため、 5つの連続したアミノ酸には 20 × 20 × 20 × 20 × 20 = 3200000 種類ものの多様な状態が存在してしまう。
つまり 本当の分子結合間の性質の解明なくして すべての組み合わせを経験的に決めることは はっきり言って不可能である。
(Fig.5) どうして炭素原子は (= 疎水性 ) は 水を嫌うのか?

炭素と水素のみを含む残基は 疎水性であることが知られている。
残念ながら MM や MD などの古典的手法では これらのメカニズムを正確に説明することができない。なぜなら それらには 電子の分布 (+ ドブロイ波 ) の概念がないからである。
一方で、通常の量子化学では 非常に弱い相互作用が重要になってくる 複雑な系で まったく役に立たない ( 解くことは もちろん不可能 )。
このページに示したように、炭素の4つの価電子はすべて 通常 他の原子と結合している。
そのため この炭素は 酸素の反発力に耐えることができない。なぜなら 炭素には フリーの価電子を調整して 酸素による反発力に対処することができないからである。
一方で、窒素や酸素原子は これらの反発力に対処する余剰の電子を持っている。
(Fig.6) ベンゼンの電子は周期的に動いている ( 重ね合わせでなく )。

量子力学 (化学) では ベンゼン環の電子は 何と非現実的な重ね合わせの状態であると主張している。
この奇妙な重ね合わせと ランダムな波束の収縮 を認めた瞬間に 私達は より動的な 電子の動きや その運動の秩序を 深く調べることを諦めざるを得なくなる。
電子やイオンの粒子は 実際には動いており、かつ 振動している。この運動状態の多様性が 体内での様々な動的な生物学的な反応を引き起こす源と言える。
多世界様の重ね合わせや 超光速の波束の収束を盲信することは それらの存在自体にリアリティーが まったくなく はっきり言って 超高性能な 生物というナノマシーン相手に 最初から白旗を挙げているに等しい。
(Fig.7) 従来の 2進数に頼るコンピューターは すでに限界に達している。

通常のコンピューターでは 打ち込まれたプログラム言語 (= 命令 ) は 最終的に2進数 (= "0" or "1" ) に変換される。
そして それをひたすら順番に読んでいくという作業を行う。
ある計算までは このスピードは 速く有用であるが、非常に多くの原子などを一気に扱おうとすると、
多大な時間を要してしまう。
例えば 現実の生物などは 非常に多くの原子、分子から構成されてはいるが、その生物学的機能は 非常に長きにわたって安定で かつ 正確である ( それらの基本的なスピードも速い )。
もちろん、これらの生物は 2進数なんてものは まったく使用していない。
これはつまり 動的な電子やイオンは 通常のコンピューターよりも はるかに高性能な機能を発揮できるポテンシャルがあると言える。
これを実現するには 非常にリアリティーのない (= 役に立たない ) 波動関数の収束や 多世界様の重ね合わせ、不確定性原理などのの概念を はやく 捨てて、現実的かつリアルな粒子の運動パターンなどを調べる作業に すぐにでも取りかからなければならない。
(Fig.7') 固体物理 → 化学 → "複雑な"分子生物学 = 変革の順番.

ご存じのとおり 地球上の生物は 非常に複雑ではあるが 高性能で安定かつ正確な ナノマシーンである。
それは 単純な結晶や 固体などより はるかに解明するのが困難である。
量子力学を捨て リアルで動的な分子相互作用を採用した際、まっ先に その変革の効果が現れるのは 物性物理学の分野ということになる。
それを実行に移すには まず パウリの排他原理の 謎に包まれた力 を明らかにすることが必須条件である。
このパウリの排他原理を明らかにしない限り 非常に抽象的な "生成消滅演算子" の束縛から 私達は 永遠に逃れることができない。非常に悲しすぎる現実である。
( もちろん このパウリの排他原理の力が明らかになった瞬間に 非現実的なスピンは 消え去るだろう。 )
一番最後に 非常に込み入った分子生物学の分野が変革し 非常に深刻な病である ALS、認知症、自己免疫疾患などに対処できるようになる日が きっと来ると思われる。
その変革が起こるまでは バイオポスドクなどの問題にもあるとおり、現在の分子生物学的研究が 実社会に役に立つことは 非常に難しいと思われる。
(Fig.8) アデニル酸キナーゼでは 基質によって どう二面角が変化するのか?

アデニル酸キナーゼ (AK) は アデノシン酸 ( ADP、 ATP、 AMP ) の変換を触媒する酵素である。
AK には オープン型とクローズ型の 2つの コンフォーメーションがあることが知られている ( それぞれ PDB 4AKE, 1AKE )。
ATP などの 基質は AK の クローズ型に結合する。
タンパク質全体のコンフォメーションは 各二面角 (ねじれ角) の値 で決まる
そこで 上記のサンプルプログラムを用いて この形態変化による 各二面角の変化を調べることにする。
(Fig.8') 二面角は最も安定な状態を意味する ( 残基 "56" CA 炭素 ↓ )

基質の存在のため、1st (= 4AKE ) と 2nd (= 1AKE ) のタンパク質の二面角は ほとんどのサイトで 少し 異なっている ( 上記のプログラムで計算 )。
この違いにも関わらず、 共通点は それらの両方のタンパク質において もっとも安定だということである。これをここで説明する。
元の角度から ±10°回転させようとすると、ある原子同士が 互いに衝突し合って それらの回転をブロックする。
この事実は このページに示したように 明らかに 両方のタンパク質において 極短に短い原子間距離が障害物として働き 各二面角を決定するファクターとして働いていることを示している。
(Fig.9) 3種類のファイルのセーブと そのフォルダの指定。

このプログラムを実行する前に、3種類のテキストファイルを コンピューター内の あるフォルダ内にセーブする必要がある。
1番目のファイル (= 1 ) は 1st AK 蛋白 (= 4AKE.txt, オープン型 ) で、 2番目のファイルは 2nd AK 蛋白 (= 1AKE.txt, クローズ型 ) である。
さらに このページに示したような アミノ酸変更操作用の 20 のアミノ酸のテンプレートファイル (= tout.txt ) をセーブする。
AK protein ( open, 4AKE.txt )
Ak protein ( closed 基質つき 1AKE.txt )
20 amino templates ( tout.txt )
Fig.9 ( 第1行 ) は ファイルを "C:\sdff" の場所のフォルダに "4AKE.txt" のファイル名でセーブするという意味である。
もし これらのファイル名や セーブフォルダ名を変更した場合は プログラム内の Fig.9 の部分 ( 青、グレー ) を変更するように。
( もちろん これらの PDB ファイルを PDB ウェブサイトから 直接セーブすることもできる。)
(Fig.10) プログラム実行後。

Fig.9 の これらのデータファイルをセーブ後、上記のサンプルプログラムを実行する。
この class file 名は "crash" なので このプログラムを "crash.java" としてセーブしてコンパイルしてほしい。
"詳細は、-Xlint: unchecked オプションを指定して再コンパイルしてください。" などの注意は無視してそのまま実行できる。
最初に コンフォーメーションが変化した 2つの AK 蛋白質の すべての二面角 (= C, CA 部分 ) を比較する。
最初の質問 (= Rotate all angles ) に対して "1" (= no ) を入力して エンターキーを押す。そして 2番目の質問 (= Compare angles ) に対して "0" (= yes ) を入力する。
Total atom ( 2nd, 1st ) は 1st, 2nd の AK 蛋白質の全原子数 ( 水素も含めた ) である。
( 各 AK は 2つのサブユニット A と B を有する。)
(Fig.11) 様々な部分の二面角。
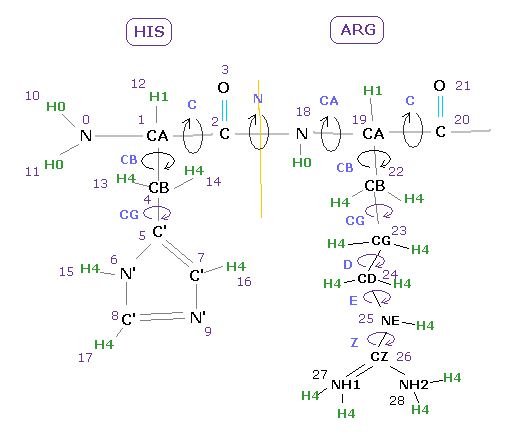
あるアミノ酸では Fig.11 に示したように 様々な回転部位がある。
最も重要な部分は 主鎖に属する "CA" と "C" である。
( "N" の部分は 2重結合性のために ほぼ 180°に固定されている。).
このプログラムでは 2nd 蛋白と 1st 蛋白の対応する二面角を引き算する ( 結果 = 2nd 二面角 - 1st 二面角 ).
例えば "5C=13.5" は 2nd と 1st の AK 蛋白の "C" 部位 (= 残基 "5" ) の角度差が 13.5°という意味である。
( つまり この部位での二面角の角度差は ほぼ同じで 13.5°だけである。)
(Fig.12) 各二面角を比較する (= 2nd 蛋白質 - 1st 蛋白質 )

残基番号 "56" のアミノ酸は 両方の AK 蛋白質で "GLY" である。
この GLY の "CA" 部分の二面角は 1st (=4AKE ) と 2nd (= 1AKE ) 蛋白質で それぞれ 67.9°と 90.8°である。
結果的に その差は 90.8 - 67.9 = 22.9° となる。
1st と 2nd の対応する部位の角度差が 10°以下のとき、この原子部位は表示されない。
( 例えば、Fig.12 で 残基 "9" は 表示されていない。これは 両 AK で 角度差がほぼないことを意味している。)
(Fig.13) y と z 幅を狭める。
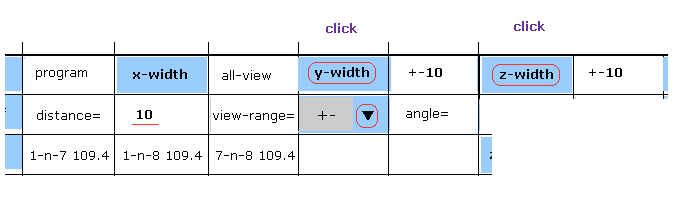
画面上では AK 蛋白質のすべての原子が表示されているため それらの位置関係を把握することは難しい。
このページに示したように 各方向に関して 幅を狭めれば、見やすくなる。
スクロールバー内の "+-" を選び、"distance=" 横のテキストボックス内に "10" を入力する。
それから "y-width" と "z-width" ボタンをクリックする。
さらに 水素原子を消去するために "hydrogen" ボタンをクリックすると、画面は より見やすくなる。
(Fig.14) タンパク質画面の一例。
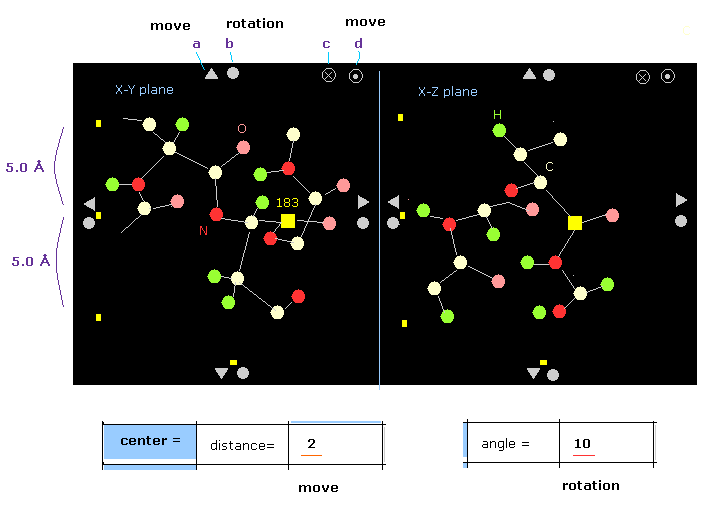
Fig.14 は あるタンパク質の一例である。
指定された原子は 黄色の四角形 (= Fig.14 の carbon-183 ) で表示されている。
例えば x-z 画面の y 方向では ±5 Å 以内の範囲のみ表示されている。
端の 三角形や円の記号をクリックすることによって タンパク質全体を 移動、もしくは 回転することができる。
(Fig.15) 1st AK タンパク質。 -- 残基 56, CA 部分。

マニュアルは このページと ほぼ同じである。
Fig.15 のケースでは、 1st AK タンパク質の 残基 "56" の "CA" の二面角を表示している。
"first"、 "residue"、 "CA" を 各スクロールバーから選び、残基番号 "56" を テキストボックス ( "from (dire)=" の隣り ) に入れ、 "dihedral" ボタンをクリックする。
この部分の二面角は 67.9°であることが分かる。
(Fig.16) 1st AK 蛋白質 -- A と B 原子の距離 ( < 3.5 Å )。

このページのように、このプログラムは A と B 原子間で 3.5 Å 未満の距離を表示する。
( 注意: ここのみ A, B は "サブユニット" の意味ではない。 )
原子 A は 残基 36 (= 56-20 ) から 残基 56 (= CA の直前 ) までにある原子である。
原子 B は 残基 56 (= CA の直後 ) から 残基 76 (= 56+20 ) までにある原子である。
"amirange" の部分の数値を変えると、この 残基の範囲を変えることができる。
56-CA の部分を回転後、 A と B の原子で 互いにぶつかるところがでてくる。
重要な点は 元の各二面角は すべての衝突を回避した 安全な状態であるということである。
(Fig.17) 1st AK 蛋白質 -- A と B 原子の距離 ( < 3.5 Å )。

コマンドプロンプト画面に これらの A-B 間の原子間距離 ( < 3.5 Å ) が表示される。
例えば、ILE (= 原子番号 767 ) と LYS の窒素 (= 830 ) の距離は 2.733 Å である。
この 2.733 Å が A と B 原子間で 最も短い距離であることが分かる。
( 他のすべての距離は 3.0 Å 以上である。)
"824" は 残基 "56" の CA 原子の プログラム原子番号 ( PDB 番号ではなく ) である。
このプログラム原子番号は 水素原子も含んでいるため PDB 原子番号よりも大きくなる。
(Fig.18) 2nd AK 蛋白質 -- 残基 56, CA 部分。

次に スクロールバー内から "second" を選んで "dihedral" ボタンをクリックする。
2nd AK 蛋白質の 対応する CA 部位の二面角は 90.8°である。
結果的に その差は 90.8 - 67.9 (= Fig.15) で 22.9°になる。
この結果が Fig.12 に示した コマンドプロンプト画面 ( 56CA = 22.9 ) のものである。
(Fig.19) 2nd AK 蛋白質 -- 残基 56, CA 部位。

Fig.16 のように、 A と B 原子間 (= ±20 アミノ酸以内 ) で 3.5 Å 以内のものが コマンドプロンプト画面に表示される。
"40824" は 2nd タンパク質の "824" のプログラム原子番号の意味である。
Fig.19 に示したように、 距離 "3.156 Å" が これらの値の中で 最も短い。
(Fig.20) この角度差の意味は何なのか ?

もちろん、基質分子は 2nd AK タンパク質 (= 1AKE ) のみに結合している。
そのため この基質の影響で これらの二面角に違いが生じるのは しごく当たり前である。
ところで これらの角度差の意味は何なのでえあろうか?
この理由を調べるのに このページに示したように これらの角度を ±10°回転させてみる。
(Fig.21) 二面角 (= 1st ) を 10°回転させる。

このページに示したように、二面角を回転させる。
スクロールバー内から "first"、 "residue"、 "CA" を選ぶ。
"56" (= 残基番号 ) と "10" (= 回転角 ) を 指定したテクストボックス内に入力する。
そして "chain rot" ボタンをクリックする。
このケースでは 1st AK 蛋白質内の A サブユニットの CA 炭素の後の原子すべてが Fig.20 の N-CA 軸を中心に 10°回転される。
(Fig.22) 回転後 短くなった原子間距離。

"chain rot" ボタンをクリックした後、コマンドプロンプト画面に 短くなった原子間距離 ( < 3.5 Å ) が表示される。
Fig.22 に示したように、 ALA の CB 炭素 (= 568 ) と LEU の C' 炭素 (= 1000 ) 間の距離は 元の長さ 3.921 Å から 1.789 Åに短くなる。
これはつまり この回転によって これらの原子が 互いに ほぼ衝突していることを意味している。
この 1.789 Å を 元の状態の最短距離 2.733 Å (= Fig.17 ) と比較するといい。
つまり この回転は 明らかにブロックされていると言える。
(Fig.23) 短くなった CB-568 と C'-1000 原子間の距離。

この距離を直接確かめたいときは、select ボタンの隣のテキストボックス内に "1000" を入力して select ボタンをクリックする ( スクロールバー内から "first" と "atom" を選択した後 )
このケースでは プログラム原子番号 "1000" が "selected" 原子として選択された。
それから "to" の隣のテキストボックス内に "568" を入力して "to=" ボタンをクリックする。
原子 568 のテキストが 上のテキストボックス内に表示される。
"1.7894" が 568-CB-ALA 部分の "dis(A)" の列に表示される。
(Fig.24) -10°の回転もブロックされる。

次に "back" ボタンをクリックして 元の角度に戻る。
次に "-10" を入力して "chain rot" ボタンをクリックする。
(Fig.25) 回転を戻す → -10°回転。

Fig.25 に示したように、ある原子間距離は短くなりすぎる (= 2.005 Å, or 2.058 Å )。
これらは Fig.17 の 元の一番短い距離 (= 2.733 Å ) よりも短くなっている。
つまり この部位では -10°回転も ブロックされているということである。
(Fig.26) 回転は 両方向でブロックされている。

この結果は 最も短い原子間距離が 各二面角を決定する際の非常に重要なファクターであることを示している。
量子化学や MM 法などは コンフォーメーションを決定する際に すべての原子のエネルギーを計算しようとする。
もちろん その計算には 多大な時間がかかり 複雑な蛋白質に実際に応用することは不可能であり 実際できていない。
また ある形態で ポテンシャルエネルギーが少し高くなったとしても それにかかる力が釣り合っていてキャンセルしている場合もあり得る。
この場合は この形態が安定であると考えられる。
このページに示したように、2つのアミノ酸の衝突が 回転全体をブロックし タンパク質の構造を決定している要因と言える。
つまり タンパク質は 一種の固体のように振舞っている。
(Fig.27) 2nd AK (= 1AKE ) で 10°回転。

回転を元に戻した (= back ) 後、スクロールバーから "second" を選び、テキストボックスに "10" を入力して "chain rot" ボタンをクリックする。
(Fig.28) 残基 56-CA (= 1AKE) で 10°回転。

Fig.28 に示したように 56-CA (= 原子番号 824 ) より後の原子すべての回転で、Fig.19 の 元の一番短い距離 3.156 Å に比べて ある原子間距離は 短くなりすぎる。
例えば、 GLY の窒素 (= 675 ) と LEU の炭素 (= 935 ) 間の距離は 短くなりすぎる (= 2.068 Å )
これはつまり これらの原子が 互いに 衝突することを意味している。
(Fig.29) 2nd AK (= 1AKE ) で -10°回転。

"=back" ボタンをクリックして元の状態に戻った後、 "-10" をテキストボックスに入力して "chain rot" ボタンをクリックする。
(Fig.30) 2nd AK (= 1AKE ) で -10°回転。

-10°回転においても、最も短い距離 2.721 Å, は 元の状態 (= Fig.19 の 3.156 Å ) のときよりも短くなる。
Fig.19 (= 元 )、 Fig.28 (= 10°回転 )、Fig.30 (= -10°回転 ) から、 二面角 90.8°が 2nd AK 蛋白質の 56-CA 部位で 最も安定であることが分かる。
(Fig.31) 二面角は 最も安定な位置を意味する。

基質の存在により、1st (= 4AKE ) と 2nd (= 1AKE ) の蛋白質の二面角は 少し異なる。
この違いにも関わらず 共通点は それら角度が 最も安定な位置であるということである。
Fig.22、 25、 28、 30 より、 元の状態から ±10°回転させたとき、両タンパク質において ある原子が 互いに衝突する。そして 一番短い原子間距離が さらに短くなる。
この事実は 明らかに 極度に短い原子間距離が 各二面角を決定するファクターとして働いていることを示している。
(Fig.32) A と B サブユニット間の衝突を加える。

アデニル酸キナーゼ (=4AKE ) は 2つのサブユニットで構成されている。
このページや 上のセクションのように A サブユニット内の原子間の衝突のみを考慮した。
実際には A と B のサブユニットは 互いに並んでおり、それらサブユニット間の最短距離は 約 3.0 Å ぐらいである。
そのため A サブユニット内のアミノ酸鎖を回転したとき、これらのアミノ酸鎖は B サブユニットに衝突する可能性がある。
上記のプログラムでは、サブユニット間や HETATM (= アミノ酸以外の原子 ) との衝突も計算できる。
(Fig.33) PDB データファイルと フォルダ名。

ここでは 下のプログラムを用いる。
( Pro-2 )
サンプル JAVA プログラム ( crash2.java )
(PDB データファイルの蛋白質)。
AK 蛋白質 ( オープン、 4AKE.txt )
20 アミノ酸テンプレート( tout.txt )。
Fig.9 で説明したとおり、これらのデータファイルを コンピューター内のフォルダにセーブした後、プログラムを実行する。
このセクションでは 1st 蛋白質のみ使用するため 2nd タンパク質のファイルは必要ない
( sfil="", ffss = 0 )。
Fig.33 のセーブしたフォルダ名は "C:\sdff" である。もし これらのファイルを異なるフォルダにセーブした場合は プログラム内のその部分を変更するように。
(Fig.34) ±10°の回転は すべての C, CA 部位でブロックされるのか?

Fig.11 で述べたように、 主鎖の ( C, CA ) 回転部位が 主に蛋白質構造全体を決定している。
上記のプログラムを実行後、 最初の質問 ( Rotate all angles ? ) に対して "0" を入力して エンターキーを押す。
次の質問に対して 再び "0" を入力して エンターキーを押す。これはつまり Aサブユニット内のみの衝突を考えるという意味である ( このページのように )。
Fig.34 は ±10°両方向回転において 249 の回転部位が ブロックされている (= both-OK ) ことを示している。
一方で 53 の部位のみ 1方向の回転がブロックされていない ( これらの部位は 通常 表面近くにある。)
この事実は 明らかに タンパク質全体の構造が すべての障害物を避けた結果であることを示している。
(Fig.35) 結果の意味。

これらの意味は このページのと ほぼ同じである。
最初に 元の状態で最も短い原子間距離を見つける。
回転によって 一番短い距離が短くなったとき、それが 回転がブロックされたとする = "OK" と画面表示。
つまり "both-OK" は ±10°回転の両方が ブロックされたことを意味している。
"20-OK" は 1方向のみが 10°回転でブロックされ、もう1方向が 20°回転でブロックされていることを示している。
"both-OK" でも "20-OK" でもないとき、もともと 2.7 Å 以下の特殊な原子間距離を除いた状態で ±10°回転がブロックされているとき "short-OK" と表す。
C 部位の回転で その C 部位に一番近い 1つの N-N 長のみを除いたとき ±10°回転でブロックされたとき、"N-OK" と表す。
それら以外で 1方向が 20°回転でブロックされていないとき、"one-NO" と表す。
(Fig.36) 結果の意味。

上のセクションと このページでは、A サブユニット内でのみの衝突を考慮した。
しかし 4AKE 蛋白質は 互いに接する 2つのサブユニット (= A, B ) を持つ。
つまり これらのケースでは 回転したアミノ酸鎖が B サブユニットの原子に衝突する可能性もある
(= B サブユニットが障害物として働く )。
上のプログラムでは、これらの衝突も考慮する。
"both-OK" 以外のケースでは、もし 回転したアミノ酸鎖が 10°回転によって B サブユニットに衝突したとき、 "both-OKab" としてカウントされる。
( A-B の crash とは A-B 間も含めて 一番短い距離が短くなり、かつ その A-B 間距離が 2.7 Å 未満になったという意味である。)
(Fig.37) A-B サブユニット間の衝突。

上記のプログラムを実行して 最初の質問 (= Rotate all angles ? ) に対して
"0" を入力する。
そして 2番目の質問 (= A-B subunit crash ) に対して "1" を入力する。
"Boundary number" は A と B サブユニット間の境界 ( < 3.5 Å ) に近い原子の プログラム原子番号である。
例えば A サブユニットの原子 (= 454 ) と B サブユニットの原子 (= 806 ) 間の距離は 2.735 Å ( < 3.5 Å ) であり、これは A と B 原子間で最も短い距離である ( 反発力のため )。
( つまり 元の状態で 極度に短い原子間距離は 力の均衡のため 排除されていると言っていい。)
これらの境界付近の原子番号をあらかじめ知っていれば、各回転で衝突を考えるとき 計算時間を節約することができる。
(Fig.38) A-B サブユニットの衝突 → ほぼすべての回転がブロックされている。

Fig.38 に示したように、非ブロック部位 ( one-No = 35 ) に対して ほぼすべての ±10°の回転が ブロックされていることが分かる ( both-OK + both-OKab + 20-OK = 358 部位 )
つまり 原子間の衝突が 各二面角を決定する 最も重要な因子であることを示している。
すべてのエネルギー準位を計算するなどという 通常の量子力学的手法に 多大な時間を浪費するよりも 古典力学的に すべての障害物を避けるということを重要視すべきであると思われる。
(Fig.39) A-B サブユニットの衝突を考慮する。 → ほぼすべての回転がブロックされている。

ここで これらの回転が 本当にブロックされているか C-175 部位を例にとって 確認する。
スクロールバー内から "atom" を選択して プログラム原子番号 "175" を入力して "dihedral" ボタンをクリックする。
175-C-LYS 部位の二面角は -22.6°であることが分かる。
コマンドプロンプト画面では 3.5 Å 未満の原子間距離が表示される。
( Fig.32 に示したように 回転部位の前後 ±20 残基以内の 原子間。 )
これらの距離の中では 2.618 Å が 最も短いことが分かる。
つまり 回転によって この 2.618 Å よりも短くなった ある原子間距離が出現したとき この元の状態のほうが バランスがとれていて安定ということになる。
(Fig.40) 175-C 部位で 10°の回転 → ブロック。

175 の炭素の後のすべての原子を回転させたいとき、 "175" と "7000" (= 最終の原子 "3355" よりも大きい任意の数 ) を指定のテキストボックスに入力して "chain rot" ボタンをクリックする。
Fig.40 に示したように、MET の炭素-5 と TYR の 炭素-358 間の距離が この 10°の回転で 上の 2.618 Å よりも短くなる (= 2.390 Å )。
これはつまり この部位での 10°回転がブロックされていることを意味している (= "OK" )。
"crash First A-sub" の欄には A と B サブユニット間で 2.8 Å 未満の距離が表示される。
例えば サブユニット A の原子 537 と サブユニット B の原子 579 は 非常に短くなる (= 0.728 Å )、これはつまり "crash" したということである。
Fig.37 に示したように、元の構造で 最も短い A-B 間距離は 2.735 Å である。
(Fig.41) 175-C 部位で -10°回転 → ブロック。

次に "=back" ボタンをクリックして 元の状態に戻り、"-10" を入力して "chain rot" ボタンを押す。
Fig.41 に示したように、 最も短い原子間距離は 2.673 Å で、これは 元の状態のときの最短距離 (= 2.618 Å ) よりも長い。
しかし 下の "crash" の欄を見ると、 サブユニット A (= 2415 ) と B (= 648 ) の原子間距離が 非常に短くなっている (= 1.659 Å ) ことが分かり、これは 2.618 Å よりも短い。
このプログラムは この部分を "-10-OKAB" と表現し、それは "both-OKab" としてカウントされる。
もちろん、見てのとおり この回転は 明らかにブロックされている。
(Fig.42) 基質 (= HETATM ) との衝突。

1AKE は AK 蛋白質の クローズ型で 基質を HETATM 原子として持つ。
( 4AKE も HETATM 原子を持つが、それはすべて H2O であるため このプログラムでは考慮していない。 )
下のサンプルプログラムを用いて、基質の存在によって 衝突がブロックされているか調べる。
( Pro-3 )
サンプル JAVA プログラム ( crash3.java )
( 蛋白質 PDB データファイル ).
AK protein ( closed, 1AKE.txt )
20 amino templates ( tout.txt )
(Fig.43) PDB データファイルとフォルダ名。

"crash3.java" の代わりに Pro2 の "crash2.java" を PDB ファイル名を変えて ( 4AKE → 1AKE ) 使用してもいい。
(Fig.44) 1AKE タンパク質で ほぼすべての回転がブロックされている。

最初に A サブユニット内でのみの衝突を考える ( A-B、A-HETATM は考えず )。
上記のプログラムを実行後、Fig.34 のように "0" と "0" を入力する。
この結果は ±10°の回転ブロック部位の数 (= 260 ) が 回転非ブロック部位の数 (= 62 ) よりも かなり多いことを示している。
Fig.12 に示したように、基質の存在によって ほぼすべての二面角が 4AKE (= オープン ) と 1AKE (= クローズ ) の間で 変化している。 ( それらの角度差は 約 10 - 20°である。 )
しかし Fig.34 と Fig.44 を比較すると、 ±10°回転は ほぼ同じ数ほど ブロックされていることおが分かる。
この事実は 基質を結合後も タンパク質の構造は すべての障害を避けるように 変化・決定されることを示している。
(Fig.45) A-B サブユニット衝突を考慮。

プログラム実行後、 "0" ついで "1" (= A-B subunit crash ) を入力すると、 Fig.38 のように A と B サブユニット間衝突も考慮される。
Fig.45 に示したように、 回転ブロック部位のトータル数 (= both-OK + both-OKab + 20-OK = 354 ) は one-No 部位 (= 40 ) に比べて 各段に多い。
つまり すでに述べたように、極端に短い原子間距離を避けることが 蛋白質の構造の決定で 最も重要と言える。
(Fig.46) A と HETATM (= 基質 ) の衝突を考慮。

1AKE 蛋白質は 基質 (= HETATM ) を持つ。
"0" 次いで "2" (= A-HETATM crash ) を入力すると、 A サブユニットと基質間の衝突も考慮される。
この基質は A サブユニットに非常に近づいているため A サブユニットの 48 もの原子が この基質から 3.5 Å 以内の距離にある。
A サブユニットと 基質間の距離は だいたい 2.7 - 3.5 Å ぐらいである。
2つの部分 (= 2.002 Å, 2.229 Å ) のみが短すぎる。なぜなら この部分で 基質が A サブユニットに共有結合しているからである。
Fig.46 に示したように、 "one-No" 部位 (= 23 ) と比べて、ほぼすべての ±10°回転がブロック ( both-OK + both-OKH + 20-OK = 380 ) されているのが分かる。
つまり タンパク質に深く入り込んだ 小さな分子や金属イオンなどは タンパク質の構造決定に際して 非常に強力なファクターであることが分かる。
次に 2PAH.txt -- hydroxylase という蛋白質について調べる。
この PDB データファイルをセーブして Fig.43 に示した crash3.java のプログラム内の "1" の部分を "2PAH.txt" に変更するように。
(Fig.47) 2PAH における回転。

Fig.47 は A サブユニット内でのみの 二面角の回転と衝突の結果である。
( プログラム実行後、 "0" 次いで "0" を入力する。 )
±10°の回転が ほぼ全ての部位 (= 403 + 132 = 535 ) でブロックされているのが分かる。
(Fig.48) 2PAH の回転 ( A-B crash も考慮 )。

"0"、次いで "1" (= A-B サブユニット crash ) を実行後入力する。
さらに ほぼ全ての部位で ±10°回転がブロックされていることが分かる。
ブロック部位 ( both-OK + both-OKab + 20-OK = 577 ) vs. one-No 部位 (= 17 ).
2J96.txt 2ISY.txt
2J0X.txt 2IU4.txt
1CTS.txt 1ROP.txt
他の PDB ファイルも試してみるといい。
ほとんどすべてのマニュアルは このページと ほぼ同じである。
"ang colo" ボタンを1回クリックすると、A サブユニット内の原子が赤色、 B サブユニット内の原子が 緑 に変わる( 1st と 2sd タンパク質両方で )。
さらにもう一回クリックすると、 1st タンパク質は赤色、 2nd タンパク質は緑色に変わる。
( さらにもう一回クリックで 元の色に戻る。 )
(M-1) "select" 原子の変更。

もし "select" 原子を変更したいときは、 スクロールバーから "first" もしくは "seond" を選んでプログラム原子番号 ( ex. 1000 ) を入力して "select" ボタンをクリックする。
M-1 のケースでは、 2nd 蛋白質の 原子-1000 を選択している。
B、 C、D サブユニット内の原子を選択したいときは、"10000"、 "20000"、 "30000" を 原子番号に足す。
( 例えば、 "11000" は B サブユニット内の 原子-1000 の意味である。 )
"to=" や "dislay" ボタンでも "first" もしくは "second" を選んだ後、 このページと同じ操作をすればいい。
(M-2) どちらが動く ?

基本的に 三角マーク (= a ) をクリックしたときは 1st と 2nd の両方の蛋白質が その方向へ動く。
"f-move" もしくは "s-move" を スクロールバーから選んだ後、このマークをクリックすると、1st もしくは 2nd の蛋白質のみ動く。 .
( もし入力値 ( "distance=" の横 ) が 20 を越えていると、移動距離は "2 Å" になる。 )
回転のケースでは 丸 (= b ) マークをクリックした時、 基本的に 1st もしくは 2nd のタンパク質のみ回転する。 時間の節約のためである。
"both" を選択後 丸マークをクリックすると、 1st と 2nd のタンパク質の両方とも 指定の角度回転する。
(M-3) 境界原子の変更。

M-3 では、スクロールバー内から "first"、 "AB"、 "No" を選択後、 "boundary" ボタンをクリックする。
このケースでは 1st タンパク質の A-B サブユニット間の境界付近 ( < 3.5 Å ) の原子のみ コマンドプロンプト画面に表示される。
その後、 "chain rot" ボタンをクリックすると、これらの衝突が考慮される。
(M-4) A サブユニット-HETATM 間の境界。

"A" と "HETATM" を選択した状態で "boundary" ボタンをクリックすると、 1st タンパク質内の "A" サブユニット内で HEATM 原子に近い原子 ( < 3.5 Å, H2O を除いた ) が コマンドプロンプト画面に表示される。
その後、 "chain rot" ボタンを使ったとき、 A-HETATM 間衝突が考慮される。
(M-5) 1st と 2nd 蛋白質の境界。

"both"、 "AB"、 "No" を選択後、"boundary" ボタンをクリックすると、 1st と 2nd タンパク質の原子で 1st と 2nd の境界に近い原子 (< 3.5 Å ) が コマンドプロンプト画面に表示される。
基本的に "No" は "HETATM crash" を考慮しないという意味である。
"AB" "No" の代わりに "AB" "AB" を選択すると、 (AB と AB 間 ), (AB と HETATM 間 ) のすべての境界を計算するため 少し時間がかかる。
"FStext" ボタンをクリックすると、 1st と 2nd のタンパク質間で 表示される テキストと粒子が変わる。
もちろん、1つしかタンパク質がないときは このボタンは意味がない。
"FSdis" ボタンをクリックすると、2nd のタンパク質が消える。
そして もう一度クリックすると、1st のタンパク質が消える。
さらにもう一度クリックすると、両方の蛋白質が現れる (= 元の状態 )。
もちろん、1つのタンパク質しかないときは このボタンは意味がない。

2013/10/19 updated This site is link free.