トップページ (2電子原子も含む正確な新ボーア模型)
ラムシフトは幻想だ!
我々の新しいボーア模型によって、ヘリウム原子の基底状態エネルギーの計算で、量子力学的な変分法よりも正確な結果をだすのに成功した。(トップページ参照のこと)。
そこで、次にリチウム原子(Lithium) とリチウムイオン (Li+) をこの新しいボーア理論によって表現できるか試してみることにする。
リチウムは、原子番号3で、周期表においてアルカリ金属に属する元素である。
それは最も軽い金属で、非常に反応しやすく燃焼もしやすい。(ただ、他のアルカリ金属よりは安定している。)
価電子は1つである。(電子配置は、電子殻が、1S × 2 と 2S × 1 である。)そのため、簡単に陽イオンになる。
高い熱と電気の伝導性をもち、リチウムイオン電池などに利用される。
自然に発生するリチウムには、Li6 と Li7 の2つの同位体があり、後者が豊富である。(92.5%)。
リチウム原子のイオン化エネルギーは、それぞれ 5.39 eV (1st), 75.64 eV (2nd), 122.45 eV (3rd) である。
つまり、リチウムイオン (Li+) の基底状態のエネルギーは、-75.64 - 22.45 = -198.09 eV である。
リチウムイオン (Li+) は 2つの電子と1つの核 (3e+) を持つ。
最初に、我々は、Fig. 1. に示すような、リチウムイオンの2つの電子が同じ1つの円軌道を核のちょうど反対側に位置する形で回っている模型を仮定する。
Fig. 1. リチウムイオン ( Li+ ) の 1 模型図

遠心力がクーロン力に等しいことより、
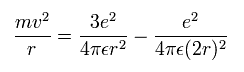
となり、ここで、r は円軌道の半径 (meter)、m は電子の質量 (me= 9.1093826 x 10-31 kg) 、e は電子の電荷 (= 1.60217653 × 10-19 C)、ε は真空の誘電率 (= 8.854187817 × 10-12 C2/Nm2) である。
円軌道の長さは、電子のド・ブロイ波の整数倍と仮定して、
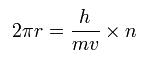
となり、ここで、h はプランク定数 (= 6.62606896 x 10-34 Js) で、h/mv はド・ブロイ波長である。
リチウムイオン (Li+) の全エネルギー (E) は、2つの電子の運動エネルギーとクーロンポテンシャル(位置)エネルギーの和であるから、
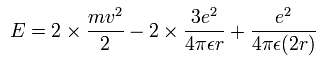
上の3つの方程式を解くと、基底状態 (n=1) のエネルギーは、-205.79 eV となる。
この計算結果は、実験値 -198.09 eV よりも低い。
(誤差は、7.7 eV もある。)
しかし、トップページでも言ったように、もし2つの電子が1ド・ブロイ波長の1つの小さな軌道に入れるとすると、これは、水素様原子の基底状態の電子がもとの軌道よりもさらに核に近い軌道を回れることになってしまう。
また、Fig.1 の軌道では、2つの電子はちょうど逆の位置にあり、それらの波の位相が互いに打ち消しあって、全体としてゼロになってしまう恐れもある。
そこで、我々は、Fig. 2. に示すような、2つの同じ形の電子軌道面が互いに垂直に交わっているという別の模型を仮定する。
トップページに示したように、我々はこの模型を使うことによって、2電子原子のヘリウムの基底状態の計算に完全に成功している。
では、この2電子のリチウムイオン (Li+) では同じようにうまくいくであろうか?
Fig. 2. リチウムイオン (Li+) 模型。 ヘリウム原子 (He) 様か ?

この模型では、電子1は、X-Y 平面、電子2は、X-Z 平面を運動している。
電子1は、(r1, 0, 0) を、電子2は、(-r1, 0, 0) を出発点とする。
詳細は、トップページを参照のこと。
ここでは、微小時間ごとに、2つの電子と1つの核 (3e+) の間のクーロン力を計算していき、Li+の2つの電子がどう運動していくか求めることにする。
この電子軌道を計算するコンピュータープログラム (class filename: MathMethod)は、JAVA (version 1.5.0) で書かれており、下のリンク先に示す。
リチウム原子核は、原点。電子1は (r1, 0, 0)を出発して、1/4 周して (0, r2, 0)に移動する。一方、電子2は (-r1, 0, 0) を出発して (0, 0, r2) に到達するとする。
ここで、次のような新しい便利な単位を使う。
MM ( 1 MM = 1 × 10-14 meter ), SS ( 1 SS = 1 × 10-22 second ) and MM/SS ( 1 MM/SS = 1 × 10-14 meter/ 1 × 10-22 second = 1 × 108 meter/second )。
このプログラムでは、最初に電子1の初期のx座標 r1 (MM) と、Li+ の全エネルギー E (eV) を入力する。その入力値から、電子の初期速度が計算され、1SS ごとに、核と2つの電子間のクーロン力を計算していく。電子1が (xx, yy, 0) にあるとき、電子2は (-xx, 0, yy ) (in MM) にある。MM を meter に x (m) = xx × 10-14. y (m) = yy × 10-14 と変換させる。
すると、電子1の加速度 (m/sec2) の x 成分は、
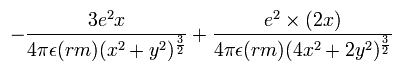
となる。ここで、最初の項は核と電子1の間のクーロン力によるもの、2つ目の項は2つの電子間の力によるもの。
リチウム原子核の質量を考えて、我々は、電子の質量中心が原点にあるときを除いて、換算質量 (rm =1/2 × (2me × nucleus)/(2me + nucleus) = 9.10794 × 10-31 kg) を使う。
同じように、加速度 (m/sec2) の y 成分は、
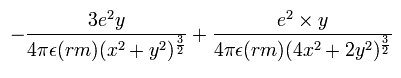
次の関係式を使って、m/sec2 を MM/SS2 に変換させる。
1 MM/SS2 = 1 × 10-14 meter/ (1 × 10-22 second)2 = 1 × 1030 meter/(second)2
この計算値をもとに、電子の位置と速度ベクトルを変化させていく。
ここでは、電子1は X-Y 平面のみを動くとしているため、電子1の加速度の z 成分は考えないことにする。もし、電子に対するクーロン力のすべての成分を考慮すると、電子の動きは Fig. 1. に示したようになってしまう。
しかし、Fig. 1. では、2つの電子が、1ド・ブロイ波長の1つの軌道におしこまれている。
我々は、ド・ブロイ波は一種の限られたスペースに関係していると仮定している。実際に、電子の2重スリットにおける移動パターンは、このド・ブロイ波によって生じる。
つまり、2つの電子軌道がある程度以上互いに近づくと、波の場が凝集して近づくのをブロックすると考える。
我々は、また、1SSごとに電子速度からド・ブロイ波長 (λ = h/mv) を計算する。
その微小な移動距離区間に含まれるド・ブロイ波 (1つの長さ λ) の数は、( この合計が WN )
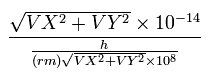
となる。ここで、( VX, VY ) は電子1の速度 ( in MM/SS )、分子は 1SS ごとに進む移動距離 (in meter)。分母は ド・ブロイ波長 (in meter ) である。
ここでは、推定される電子軌道をこの計算のために10万以上の微小区間に分割している。
電子1が、1/4 周して、その x 座標がゼロになったとき、このプログラムはその地点での電子1の速度の y 成分 (last VY とする) をチェックする。
もし、この last VY がゼロのとき、2つの電子は周期的に核の周囲の同じ軌道を回ることになる。
それで、-0.0001 < last VY < 0.0001 (MM/SS) が満たされるとき、このプログラムは画面上に次の値の結果を表示する。
r1, VY, preVY (1 SS 前の last VY), (mid)WN ( 1/4 周に含まれるド・ブロイ波の総数 )。
Table 1 は、last VY がゼロに最も近いときの結果を示す。
Fig. 3. は、Table. 1.の結果をグラフにしたものである。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -185.0 | 2092.0 | 0.25928 | 1.03712 |
| -190.0 | 2036.5 | 0.25585 | 1.02340 |
| -195.0 | 1984.5 | 0.25255 | 1.01020 |
| -199.0 | 1944.5 | 0.25000 | 1.00000 |
| -205.0 | 1888.0 | 0.24631 | 0.98524 |
| -210.0 | 1843.0 | 0.24336 | 0.97344 |
| -215.0 | 1800.0 | 0.24051 | 0.96204 |
Fig. 3. Li+ の様々なエネルギーレベルのときの1軌道に含まれるド・ブロイ波の総数。
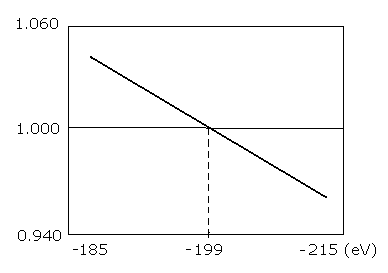
Table 1. と Fig. 3 に示されたように、Li+ の全エネルギー (E) が、-199.0 eVのとき、 WN × 4 はちょうど 1.00000. となる。
実験値は、-198.09 eV である。そのため、この計算結果 -199.0 eV は実験値 -198.09 eV にほぼ一致している。。
つまり、この結果は、リチウムイオン(Li+)においても、2つの電子の軌道面が、ヘリウム原子のように互いに垂直に交わっていることを示している。
(誤差はたったの 0.91 eV ( 0.5% 未満 )である。この誤差はおそらく、リチウムイオンがヘリウム原子より不安定なため、軌道面が完全には Fig. 2.の状態を保ってないためによるものと考えられる。)
次に、リチウム原子 (Li) に挑戦することにする。
リチウム原子は、1S軌道に2つの電子と、2S軌道に1つの電子をもっている。
1Sの2つの電子は、3e+ の原子核に強くひきつけられているため、2S の電子に比べてかなり原子核に距離的に近いところにある。
つまり、近似的に、我々は2S電子が、 +e 原子核 (+3e - 2e = +e) の周りの2ド・ブロイ波長の円軌道を回っているとみなすことができる。
(これは、我々が2S電子において、近似的に水素原子の式を使えることを意味する。)
ボーア模型によれば、2ド・ブロイ波長の軌道の半径 (Rb) は、次のように ( 4 × ボーア半径 ) となる。
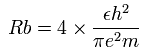
計算すると、この Rb は 2.1167 × 10-10 meter ( = 21167 MM ) となる。
次に n = 2 のエネルギー準位 は、 (水素原子のエネルギー準位の式を使って)
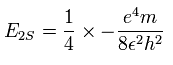
となる。そのため、中性のリチウムの原子模型をつぎのように仮定する。
Fig. 4. リチウム原子 (Li) 模型
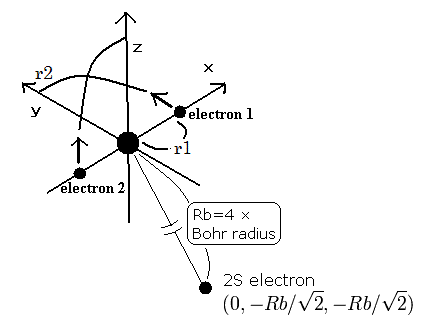
1Sの2つの電子はなるべく2S電子を避けるように運動する。そこで、我々は2S電子を Fig. 4. に示すように ( 0, - Rb / √2, - Rb / √2 ) に固定する。
(Fig. 4. は3つの電子の相対的な位置関係を示している。実際は、この2Sの電子は1Sの電子よりもゆっくりと核の周りを周回している。)
Li+ のように、電子1が、(x, y, 0) にあるとき、電子2は、 (-x, 0, y) にある。
つまり、各粒子間の距離は、
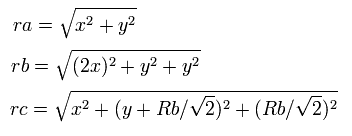
となる、ここで、ra は電子1と核の距離、rb は2つの 1S 電子間の距離、rc は電子1と 2S の電子の距離である。
電子1の加速度 (m/sec2) の x成分は、
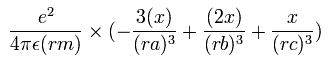
となる。
同様に、電子1の加速度 (m/sec2) の y成分は、
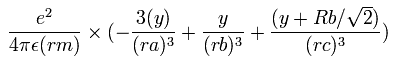
となる。
また、Li+ のときのように、1S 軌道の 1/4 周に含まれるド・ブロイ波の数を計算する。
Sample JAVA program (Li 原子)
Table 2 は、Li 原子において、 last VY がゼロに一番近い時の結果を示す。
| E (eV) | r1 (MM) | WN | WN x 4 |
|---|---|---|---|
| -190.00 | 2086.0 | 0.25860 | 1.03440 |
| -195.00 | 2031.0 | 0.25518 | 1.02072 |
| -200.00 | 1979.0 | 0.25190 | 1.00760 |
| -202.97 | 1949.0 | 0.25000 | 1.00000 |
| -205.00 | 1929.0 | 0.24874 | 0.99496 |
| -210.00 | 1882.0 | 0.24569 | 0.98276 |
| -215.00 | 1837.0 | 0.24276 | 0.97104 |
この結果は、Li 原子の基底状態エネルギーが -202.97 eV のとき、軌道の長さがド・ブロイ波長の ちょうど 1.00000 倍になることを示している。
Li 原子の実験値は -203.48 eV である。
つまり、計算誤差は、わずか 0.51 eV ( 0.25 % ) である。
(この小さな計算誤差は、おそらく、”近似的な”2S電子軌道を用いたことによると考えられる。)
このことは、リチウム原子の3つの電子が、 Fig.4. に示すように運動していると言ってほぼ間違いないということを意味する。
このページ (ボーア模型における 1S と 2S 電子の関係) も参照のこと。
もし、我々がリチウム (Li) とリチウムイオン (Li+) をボーア模型によって正確に表現することができたら、この方法を拡張して、他の原子(ベリリウム (Be) 、ホウ素 (B)、炭素 (C) ) に拡張することが可能となる。

2010/7/16 updated This site is link free.