
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。
タンパク質構造操作マニュアル。
(Fig.1) どうして 量子力学は タンパク質相互作用計算に利用できないのか?

すてに述べたとおり、多原子の波動関数 ( シュレディンガー方程式 ) を解くことは 難しすぎて 実際のタンパク質相互作用計算においては 使い物にならない。
シュレディンガー方程式を用いて マクロの分子を計算するには、人為的に ある有限な数の基底関数を選択する必要がある。
もちろん 小さい基底関数では 正確なエネルギー状態を得ることは不可能であり、異なった基底関数の選択ごとに 様々な異なった誤差が 発生する。
タンパク質相互作用を決定する 水素結合や ファンデルワールス力のエネルギーは 共有結合の 10分の1 以下である。
例えば、単一の酸素原子の 1-6 の全イオン化エネルギーは 433.11 eV で、これは 共有結合 (= 約 3.0 eV ) や 水素結合 (= 約 0.1 eV ) に比べて 非常に大きい。
そのため 異なった基底関数の選択による タンパク質全体におけるエネルギー誤差が これらの小さな結合エネルギーよりも はるかに大きくなってしまう。
密度汎関数法 (= DFT ) は "ab-initio" ではなく、また "LDA" などの かなり粗い近似に頼っているため、様々なタンパク質相互作用に使えない。
私達は 数学と化した量子力学的波動関数を諦めて、もっと実在的な 各価電子や原子核に作用する 実際のクーロン力などを考慮する必要がある。
(Fig.2) 80 年以上も経過した。 → 量子力学は役に立たない。
ご存じのとおり、量子力学 ( QM ) が誕生してから かれこれ 80年以上もの長い時間が経過した。
それだけ 長い時間が経過して、その間 世界中の 無数の研究者が
様々な高性能のコンピューターを駆使しても 量子力学 ( や量子化学 ) の波動関数は 医療や工業などの実際の現場に使われていない。
( 例えば 分子生物学関連の論文見ても、波動関数なんてものは まったく皆無である。)
これらの事実は 私たちが 役に立たない量子力学に頼る限り 様々な複雑なタンパク質相互作用 ( しいては 深刻な病 ) などの解明ができないことを示している。
( なぜなら もうすでに 80 年以上も経過した結果が 今の現状だからである。)
(Fig.3) "Shut up and calculate !" → 永遠に先に進めない。

もちろん、タンパク質相互作用は複雑で それらの具体的なメカニズムの解明は非常に難しいことは理解できる。
しかし 真の問題は 別のところにある。
現在の量子力学が 複雑なマクロの分子を扱うことができず その限界に達しているにも関わらず、彼らは 波動関数の実態や スピンの本当の意味を解明して より簡単な計算手法を見つけ出そうと 決してしないことにある。
お気づきのとおり、もし これらの概念が実際に何なのかを問うことを諦めれば、これらの分野で 先に進むことは絶対に不可能である。
この矛盾した量子力学の姿勢こそが 最も憂慮すべき深刻な問題である。
(Fig.4) 分子力学法には 電子という概念がない。

分子力学法 ( MM 法 ) は 分子間相互作用を 古典力学的に考え直したものである。
複雑すぎて役に立たない量子力学の波動関数のために、大きな分子では この分子力学法が
量子化学の代わりに用いられている。
MM 法では 結合長や結合角などが 古典的な "バネ" のように扱われている。
最も重要な問題は MM 法には 電子という 概念が ないということである。
つまり これらの古典的な電位は 経験的 (= 第一原理ではなく ) に決める必要がある。
しかし例えば アミノ酸は 20 種類存在するため、 5つの連続したアミノ酸には 20 × 20 × 20 × 20 × 20 = 3200000 種類ものの多様な状態が存在してしまう。
つまり 本当の分子結合間の性質の解明なくして すべての組み合わせを経験的に決めることは はっきり言って不可能である。
(Fig.5) 量子力学の広がった電子雲 → 全電荷 = ゼロ !?

ご存じのとおり、各電子は 現実には 電子雲なんかでなく、個々に分離していることはいうまでもない。
実は この現実的に分離した電子分布というのが 古典軌道による分子結合に関して 重要な鍵となる。
量子力学や化学は この現実的で"分離した"電子の概念を使用できない。なぜなら ボーア模型に置き換わった量子力学の波動関数は滑らかに分布しているからである。
しかしもし 電子が量子力学のように あらゆる場所に細かく分離して広がっていると 例えば 電子軌道半径の違いなどがなくなってしまう。
なぜなら ご存じのとおり、無限小の電荷 (電子) が ある球面上に広がって分布しているとき、そのポテンシャルエネルギー V は この球がいかなる半径でも同じになってしまう。
( この ポテンシャル V は 球の中心からの距離のみの関数である。)
そのため 例えば、フッ素と塩素の違いが
なくなってしまい、同じ量のプラスとマイナスの電荷がちょうど打ち消しあって 常に 全電荷がゼロになってしまう。これは非常に奇妙である。
(Fig.6) H-H 結合 = 2つの電子が 互いに避け合っている。
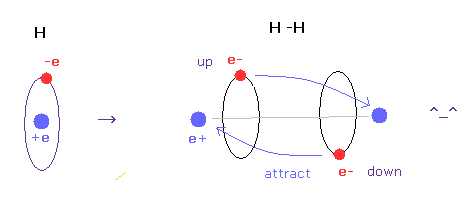
このページで示したように、古典的軌道を持った 非常に簡単な自然な方法で 水素分子の正確な実験値と H-H 結合の 本当の意味を見つけることができた。
この計算において 重要な鍵は 2つの電子が 実際に 互いに避け合っている ( up と down に ) という点にある。
もし これらが避け合っていないと H2 の正確な結合エネルギーを得ることは不可能である ( 確かめてもらってもいい )。
残念ながら 量子力学の波動関数は この避け合う効果を シンプルなモデルを用いて表すことができない。
それは 非常に複雑な 行列式 (= 排他原理 ) や ヒレラス関数に頼らなければならず、マクロな分子に応用することは不可能といっていい。
このページのこのプログラムを実行すると、もう一方の原子側に 突き出た価電子 "e0" が 様々な共有結合長を決定する際の キーファクターであることが分かる。
(Fig.7) C の電子に作用する力の比較。
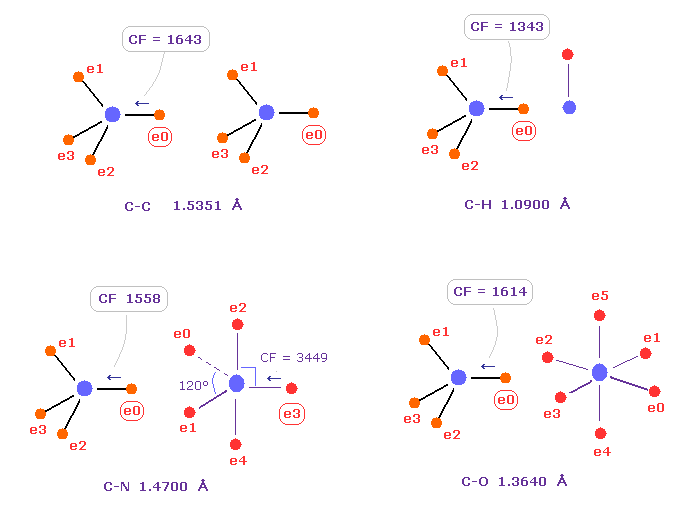
Fig.7 は C-C、 C-H、 C-N、 C-O のシングル結合における 炭素の電子 e0 に作用する力 CFを示したものである。
炭素が 様々な結合において 正四面体構造を 保っていることを考慮すると、炭素の電子に作用する力が 互いに ほぼ 等しくなるのが自然である。
実際に これらの力 (= CF ) は 異なった C-C、C-H、C-N、C-O 結合において それぞれ 1643, 1343, 1558, 1614 になる。
( これらの結合長は 実験値である、C-O の シングル結合は 酢酸からのものである。 )
| 分子結合 | 結合長 | e0 への力 |
|---|---|---|
| C - H | 1.0900 Å | CF = 1343 |
| C - C | 1.5351 Å | CF = 1643 |
| C - N | 1.4700 Å | CF = 1558 |
| C - O | 1.3640 Å | CF = 1614 |
| C - F | 1.3500 Å | CF = 1605 |
| C - Si | 1.8500 Å | CF = 1602 |
| C - P | 1.8400 Å | CF = 1584 |
| C - S | 1.8200 Å | CF = 1708 |
| C - Cl | 1.7700 Å | CF = 1626 |
Table 1 は 様々な結合における 炭素の電子 "ele 0" に作用する力 (= CF ) を示したものである。
驚くべきことに、異なった結合において、これらの力 (= CF ) は ほぼ 同じになる。
これはつまり 共通のメカニズムが働いて、炭素の正四面体の構造が 様々な結合において 保たれていることを示している。
Fig.5 で述べたように、 "分離した" 電子の概念が重要なキーポイントである。なぜなら これらの結合長の違いは 明らかに 分離した電子概念がないと実現できないからである。
例えば、塩素では その原子核が 3ドブロイ波長のために より露出しているため、力 CF が 他の結合と同じになるためには 結合長が長くなる必要があると言える。
(Fig.8) どうやって 原子は立体障害と共有結合を区別するのか?
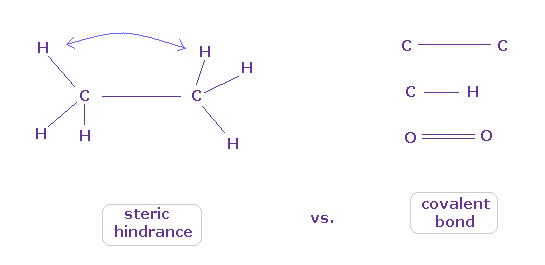
よく教科書で "エタンの6つの水素原子は 互いに避け合う配置をとる" とか "タンパク質の構造は その立体障害のために 非常に制限される " だとかの説明を見られるかもしれない。
これはつまり 各原子は 必ず 他の原子を避ける傾向があるということだろうか?
一方で 希ガス原子を除いて 様々な原子は 安定な共有結合を形成することができる。
各原子が 互いに"避け合う"のに、どうして それらは 安定で タイトな共有結合を形成することが可能なのだろうか?
(Fig.9) レナード・ジョーンズポテンシャルは 共有結合への移行を説明できない。
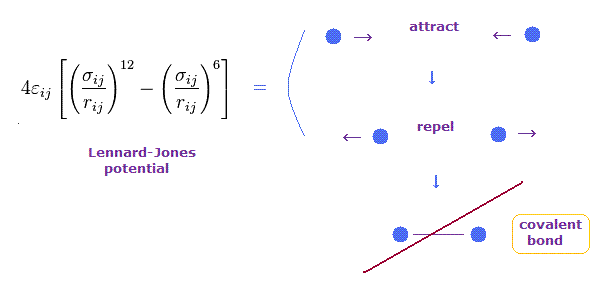
レナード・ジョーンズポテンシャルは ファンデル・ワールス力などの分子間力を表すのに よく使用される。
このポテンシャルでは、2つの粒子間の距離が 非常に 長いとき、それらは 互いに弱く引き合う。
一方で、2つの粒子が ある閾値の結合長よりも近づくとき、それらは 互いに避け合うことになる。
この反発力は 電子雲の衝突とパウリの排他原理によると 彼らは主張している。
しかし このレナード・ジョーンズポテンシャルは もっと短い結合長において どうして非常に安定かつ タイトな共有結合が形成されるのかを説明することができない。
(Fig.10) C-C = 1.5400 Å は 釣り合いのとれた長さである。
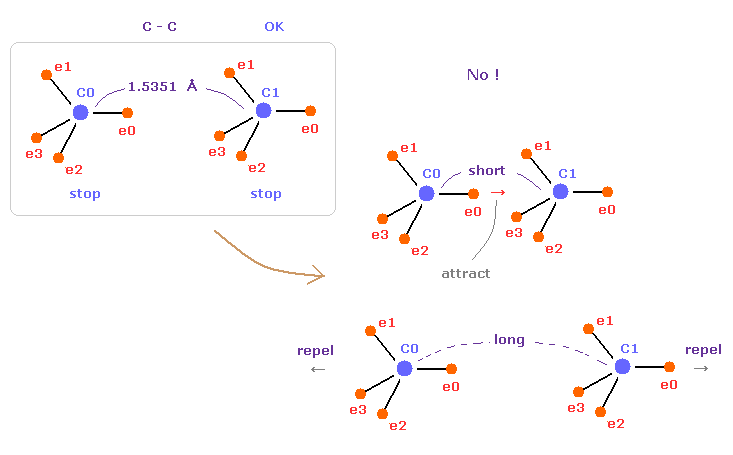
このページでは エタンの C-C 結合長 1.5351 Å が 両方の C 原子核の安定性にとって 必要不可欠なものであることを示した。
もし C-C 結合長が 1.5351 Å よりも短くなると、e0 と C1 間の引力が 強くなりすぎ、不安定になる (= 電子の周期運動も壊れる。 )。
そして もし C-C 結合長が これよりも長くなると、2つの C 原子核間の反発力が優勢になり 不安定になる (= 結合エネルギーが 負の値になる。)。
これが C-C 結合長を決定する 本当のメカニズムである。
(Fig.11) 結合長が "長い" か "短い" かにより その性質が決まる。
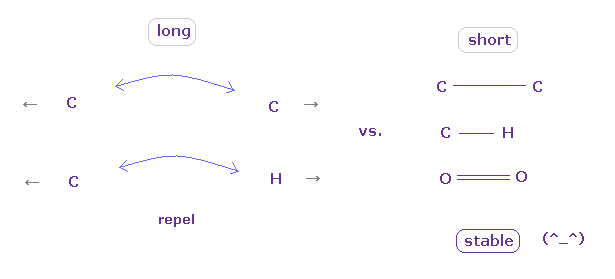
結論からして、安定な結合を形成するには、2つの原子が ある閾値の長さよりも 互いに 接近する必要があると言える。
その閾値の長さよりも 長いと、 電子間や核間の反発力 が 優勢になり、いわゆる 立体障害を引き起こす。
2つの原子が 互いに ある閾値よりも近づくと、突き出た電子 ( Fig.7 の "e0" ) の引きつけ力が強くなり 原子核間の反発力をキャンセルする。
また これらの短い共有結合長では、2つの原子の電子が 互いに周期的に避け合う傾向になり、これが 結合エネルギーの源になる。
( これらの 周期的に避け合う運動パターンは 非常に長い結合長では 形成しにくいと考えられる。)
通常のタンパク質では、2つの原子間の ほぼすべての距離は 共有結合長よりも 長いため、それらは 立体障害を引き起こす。
(Fig.12) グルカゴンの構造は体内で変化している。
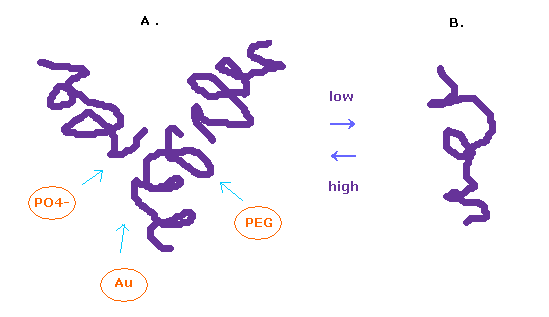
グルカゴンの構造が 周囲の環境に応じて 容易に変化することは知られている。
高濃度の溶液中では グルカゴンは 3量体を形成し、低濃度では分離する。
タンパク質の構造を観察するためには たくさんのグルカゴンをくっつけて 結晶化させる必要がある。
このときには PEG、 バッファー、塩、金属などの様々な物質を用いる。
この仮定において 各タンパク質は 様々な溝にはまって 結晶化することになる。
このページでは 単一の分離したグルカゴンの構造を調べる。
そのため これら他の様々な周囲にくっついた物質などの影響も その解釈には考える必要がある。
(Fig.13) グルカゴンの 3次元 構造。

グルカゴンは たった 29アミノ酸からなる非常に小さなタンパク質である。
そのため この単純なグルカゴンからスタートするのが妥当である。
ここでは 次のサンプル JAVA プログラムを用いる。
サンプル JAVA プログラム ( PDB タンパク質 )。
詳細なマニュアルに関しては このページを最初に参照するように。
グルカゴンの PDB のデータ ( 1GCN ) は、
このテキストは "glucagon6.txt" というファイル名で 場所 "C:\sdff" のフォルダー内に保存する。
その後、上記のサンプル JAVA プログラムを "protein.java" としてセーブしてコンパイルしてほしい。
”詳細は、-Xlint;uncheckedオプションを指定して再コンパイルしてください。”の 注意は無視して実行できる。
(Fig.14) プログラム内のフォルダー名の変更。

もし このテキストを別のフォルダーにセーブした場合は 上記のプログラム内の青線の部分を このセーブしたフォルダなどに変更するように。
( Fig.14 の 青線部分を変更するように。)
(Fig.15) 水素原子の反発力は非常に弱い。

このプログラムを実行後、 各原子の ポテンシャルエネルギー (= alV ) 部分を見る。
このポテンシャルエネルギーは 各原子近くの固定エリアを除いて計算されている。 このページも参照のこと。
"Atom" ボタンをクリックすると、 次のページに進める。
一目見て 水素の反発ポテンシャルエネルギーは 酸素、窒素、炭素などの他の原子に比較して 非常に弱いことが分かる。
( このプログラムでは 正の値 = 反発する V, 負の値 = 引きつける V。 )
なぜなら 水素の原子核は たった +1 の正電荷で、かつ この原子核が露出しているからである。
(Fig.16) バリンの 3次元構造。どうして "A" の方がよく見られる?

バリンでは Fig.16 の A のコンフォーメーションが B に比較してよく見られる。
なぜなら Fig.15 に示したように、CH3 の部分が 単一の水素原子よりも より強い反発力を発揮するからである。
そのため CH3 は 窒素と酸素を避ける傾向にある ( これらの反発力も強い。)
このことが A のコンフォーメーションが よく見られる本当の理由である。
ここでは 様々な2原子間の相互作用を調べるのに このページの このプログラムを用いる。
(Fig.17) H -- O-H 水素結合。
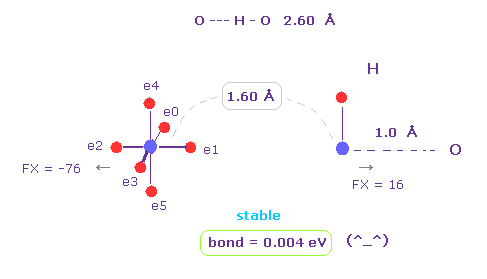
H -- O-H 水素結合長は 約 2.60 - 2.70 Å である。
A と B 原子 として "O" と "H" を選び、 核間距離を "1.60 Å" (= 16000 MM ) にする。
x-y 平面上で "O" 原子を 45°回転する ( "45" を入力して "x-y ang" ボタンをクリックする。 )
このケースにおいても、結合エネルギーは 正 (= 0.004 eV ) になり、O-H 結合は 安定になる。
また 原子間の反発力は ほぼ ゼロ ( FX = -76, FX = 16 ) になる。
( これらは ほぼゼロだが、わずかに "反発" しているため、 O-H や N-H 結合長は これ以上 短くなれない。 )
| O - A 長 | 1.90 Å | 1.80 Å | 1.70 Å | 1.60 Å | 1.50 Å | 1.40 Å | 1.30 Å |
|---|---|---|---|---|---|---|---|
| O - H | -0.011 | -0.009 | -0.004 | +0.004 | +0.022 | +0.054 | +0.113 |
| O - C | -0.205 | -0.190 | -0.158 | -0.095 | +0.020 | +0.232 | +0.612 |
| O - O | -0.261 | -0.266 | -0.265 | -0.252 | -0.215 | -0.122 | +0.092 |
一見して 水素原子の反発力が これらの短い分子間距離においても 非常に弱いことが分かる。
例えば、1.60 Å における O-O の相互作用の結合エネルギーは 負であり、その絶対値はかなり大きい。 (= -0.252 vs. +0.004 )
( このプログラムでは 結合エネルギーが負のとき、そららは 互いに 反発しあうことを意味している。 )
これはつまり、2つの酸素原子が ここまでの短距離まで 互いに近づくことは 非常に難しいことを意味している。
(Fig.18) 力 = 1000.
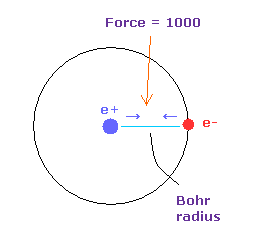
力の単位は Fig.18 に示したものを使う。
水素原子の基底状態で 電子 と +e の原子核間の距離が ボーア半径のとき、その力を 1000 とする。
例えば 1468 の力は H 原子の基底状態のときの力の 1.468 倍ということになる。
| O - A 長 | 1.90 Å | 1.80 Å | 1.70 Å | 1.60 Å | 1.50 Å |
|---|---|---|---|---|---|
| O of ( O - H ) | 38 | 47 | 58 | 74 | 94 |
| H of ( O - H ) | 19 | 20 | 22 | 25 | 26 |
| O of ( O - O ) | 121 | 132 | 144 | 256 | 167 |
このプログラムを用いると 2つの原子が互いに近づくにつれて、反発力が強くなることが分かる。
これが 分子結合長が ある閾値よりも短くなれない理由である。
( もちろん すでに述べたように 結合長が かなり短くなると、安定な共有結合が形成される。)
Table 3 に見られるように、O-O 相互作用における反発力は O-H 結合に比較して 非常に強い。
( これらの反発力は 酸素の電子を x-y 平面で 45°回転させたときとしてないときの平均値である。)
実際に 様々なタンパク質において、O-O の原子間が これほど短くなるのは見られない。
おそらく、O-H における 1.70 Å と 1.60 Å の間あたりの力が 反発力の上限値であろうと考えられる。
(Fig.19) コマンドプロンプト。

このプログラム実行後、Fig.19 の値が コマンドプロンプト画面上に表示される。
例えば、 "H:13-H:24= 1.2918" は 水素原子 "13" と "24" (= 絶対原子番号, このページも参照のこと。 ) の間の距離が 1.2918 Å であることを意味している。
上のセクションで述べたように、強くなる反発力のために、原子間距離 (= 共有でない ) には ある 下限があると考えられる。
これらの値は グルカゴン全体における これらの下限付近の長さを示したものである。
( H-H= 1.3 Å, O-O, N-O, C-O = 2.6 Å, C-C, C-N, N-N = 2.5 Å, O-H, N-H, C-H = 1.7 Å. )
(Fig.20) O-O 長 = 2.557 Å

Fig.19 に示したように、 グルカゴンにおける O-O の分子間距離の下限は 2.5577 Å である。
O-O 分子間距離が この値のとき、平均の反発力は 約 70である。
実際に 酸素 56 と 58 間の反発力は このプログラムにおいても 約 70 ぐらいである。
( 詳細は このページを参照のこと。)
| O - O 長 | 5.0 Å | 4.5 Å | 4.0 Å | 3.5 Å | 3.0 Å | 2.5 Å | 2.0 Å |
|---|---|---|---|---|---|---|---|
| O1 of ( O - O ) | 19 | 23 | 30 | 39 | 53 | 78 | 125 |
| O2 of ( O - O ) | 19 | 23 | 29 | 38 | 51 | 71 | 97 |
| Average force | 19 | 23 | 29.5 | 38.5 | 52 | 75 | 111 |
Table 4 は このプログラムを使ってだした 様々な分子結合長における反発力を表したものである。
見てのとおり、力の変化は 2.6 Å 長以下のとき 特に大きくなる。
おそらく このことが O-O 原子間距離が 立体障害によって ある値よりも近づけない原因と考えられる。
(Fig.21) N-O 長 = 2.600 Å

グルカゴンにおける N-O の原子間距離の下限も 約 2.600 Å である。
N-O の原子間距離が この値のとき、反発力は N で57、 O で 70 となる。
つまり このケースでも 分子相互作用における最大の反発力は 約 70 ということになる。
(Fig.22) H-H 長 = 1.290 Å

グルカゴンの H-H 原子間距離の下限は 約 1.290 Å である。
H-H 原子間距離が この値のとき、 平均の反発力は 26 である。
水素は たった1つしか電子しかないため、酸素や窒素のように より強い反発力を処理する力がない。
重要な点は H-H の場合、結合エネルギーは 正 (= 0.381 eV ) の値になり、これはつまり 安定な結合を意味している。
しかし もちろん この安定な結合エネルギーを得るには H-H の2つの電子は 周期的に互いに避け合う必要がある (= up と down )。
基本的に 水素原子は 炭素や窒素などの他の原子と結合していて それらとすでに同期している。
そのため それが他の水素とまで同期する余裕はないと言っていい。
(Fig.23) 水素の軌道は 傾くことができる ?

基本的に 2つの水素原子間の距離が非常に短いとき、Fig.23 のコンフォーメーションは不可能と言える。
なぜなら Fig.23 では "a" の地点の価電子が 他の水素原子核に強く引きつけられるため、基本的に "b" の位置まで正常に戻ってこれない。
また Fig.23 では 引きつけ力や結合エネルギーが 非現実的に強くなりすぎる。
H-H 距離は 通常 他の原子間距離に比較して短くなるため その解釈には十分注意する必要がある。
(Fig.24) 平均の水素原子の電子分布

このプログラムでは、 Fig.24 の平均の水素の電子分布を用いた。
ここでは 1つの -e の電子の代わりに 4つの -0.25e の電子を用いている。
2つの原子が 互いに非常に近づくとき、Fig.22 のような 避け合う効果を考慮する必要がある。
しかし このプログラムでは この効果まで考慮していないため、特に短くなった原子間距離に関しては ポテンシャルエネルギーに加えて 力なども考慮に入れる必要がある。
(Fig.25) C (= "2" ) における アミノ酸鎖回転後の 力の変化。

このページに示したように、アミノ酸鎖を
2-C-HIS (= ヒスチジン、炭素 "2" ) において 10°回転させ、そのポテンシャルエネルギーの変化を調べる。
2-C 炭素の後のすべてのアミノ酸を回転させたいため "500" (= トータルの原子数以上の数 ) を "to=" のテキストボックス、
"2" を "from (dire)=" のテキストボックスに入力して "chain rot" ボタンをクリックする。
アミノ酸鎖回転後は すべての相互作用を計算するのに少し時間がかかる。
この回転後、二面角は -159.3° から -149.3°に変化する。 ( 確かめるといい。 )
" =back " ボタンをクリックすると、回転前の元のタンパク質構造に戻る。
(Fig.26) コマンドプロンプト。

アミノ酸鎖回転後、結果の一部がコマンドプロンプト画面に表示される。
基本的に 非共有結合は 反発力が増強するため 許される最短の距離というものが存在すると考えられる。
Fig.26 の最初の行では、 HIS-CB-4 (= ヒスチジン側鎖、 炭素 ) と SER-N-18 (= セリン主鎖、窒素 ) 間の距離が 短くなりすぎることを示している ( 2.5407 Å → 2.4867 Å )。
この原子間距離は 立体障害を考慮すると 短すぎると考えられる。
"Energy change = 0.5470 (eV) " は このアミノ酸鎖回転により、全ポテンシャルエネルギーが 高くなることを表している。
つまり この回転は起こりにくく、元のタンパク質構造が安定であることを意味している。
(Fig.27) 18-N-SER におけるエネルギー変化。

Fig.26 の "Plus" の行は ポテンシャルエネルギーが特に大きくなった原子をピックアップしたものである。
"18" (= 絶対原子番号 ) を入力して "select" ボタンをクリックする。
そして "V change" ボタンをクリックして、 それから"FX rela" ボタンをクリックする。
Fig.27 に示したように、18-N-SER の ポテンシャルエネルギーの変化 (= c,aV ) は +0.1271 eV である。
15、 16、 17-H4-HIS の " dis (A) " の列では、 18-N-SER (= セリン主鎖、窒素 ) と ヒスチジンの側鎖 (水素) の距離が 短くなっていることを意味している。
( 例えば、 "cha-0.1867" は 18-N-SER と 15-H4-HIS の間の距離が 0.1867 Å 短くなったことを意味している。)
(Fig.28) 18-N-SER のポテンシャルエネルギーが 高くなった理由。
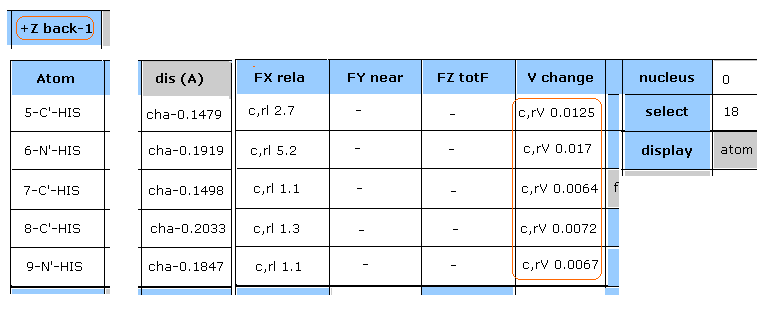
水素のエネルギー変化は Fig.27 に示したように無視できるぐらいである。
それから "+Z back-1" ボタンを2回クリックして 2ページ前に戻る。
Fig.28 では、 ヒスチジンに含まれるすべての原子のポテンシャルエネルギーが高くなったことを表している。なぜなら それらが 回転によって 18-N-SER に近づいたからである。
(Fig.29) ヒスチジン → 18-窒素。
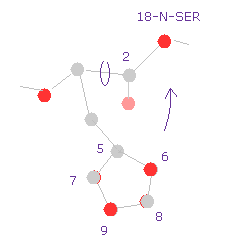
つまり ヒスチジン側鎖とセリン原子間の距離が短くなったことが 全ポテンシャルエネルギーが 回転によって高くなった 主要な要因である。
注意:Fig.26 のポテンシャルエネルギー変化は 各原子から 5.0 Å 以内の原子間相互作用のみ見ている。
そのため このエリアの原子数が増加したとき、このポテンシャルエネルギー変化は 各ポテンシャルエネルギー変化の総和と等しくなくなる。
( 各ポテンシャルエネルギー変化は 6.0 Å から 4.9 Å に変化するケースなども含まれている。つまり 最終の距離のみが 5.0 Å 以内のときも エネルギー変化が計算されている。)
(Fig.30) ヒスチジン → グルタミン。

次に " =back " ボタンを押して、 元のコンフォーメーションに戻る。
"angle=" ボタンの横に "-10" を入力して"chain rot" ボタンをクリックする。
コマンドプロンプト画面に表示されたように、2-C で -10°回転のときも ポテンシャルエネルギーが 高くなる (= +1.1613 ).
例えば、ヒスチジン側鎖の "8" の炭素を選択すると、ヒスチジンとグルタミン (= GLN ) 間の距離が短くなったことが このエネルギー変化の主要な要因であることが分かる。
これはつまり ヒスチジンの側鎖は セリンとグルタミンの間に
挟まれていると言える。
(Fig.31) 20-C-SER で回転 (+10°)

次に 20-C-SER のところで 10°回転させる。
"=back" ボタンをクリックして、 "20" を "from (dire)=" の横、 "10" を "angle=" の横のテキストボックス内に入れ、 "chain rot" ボタンをクリックする。
このケースにおいても、全ポテンシャルエネルギーは 高く (= +0.4650 eV ) なる。なぜなら ヒスチジンの側鎖が グルタミンに近づくからである。
( つまり 原子 "5","6","8" (= HIS ) と "33", "34", "35", "36" (= GLN ) のポテンシャルエネルギーが増加する。 )
(Fig.32) 20-C-SER で回転 ( -10°, -20° )

次に 20-C-SER で -10°回転させる。
"=back" ボタンをクリックして、 "-10" を "angle=" の横に入力して "chain rot" ボタンをクリックする。
このケースでは 全ポテンシャルエネルギーが少し低くなる。なぜならヒスチジンの側鎖が グルタミンから離れるからである。
( つまり 原子 "8","9" (= HIS ) と "33", "34", "36" (= GLN ) のポテンシャルエネルギーが "Minus" 行に示したように 低くなる。)
"chain rot" ボタンを もう一度クリックする。つまり トータルで -20° 回転したことになる。
このケースでは、ヒスチジンが 今度はグリシンの原子に近づくため 全エネルギーが高く ( +0.1650 eV ) なる。
( つまり この回転には いくらか余裕があると言える。)
(Fig.33) "すきま”が 他のタンパクや塩で埋まる。

問題はグリシン近くなどの 可変部分は タンパク質結晶内では 他のタンパクの突起やら塩で 固定されている点である。
なぜなら たくさんのタンパク質をくっつけさせることが タンパク質結晶解析にとって必要不可欠だからである。
そのため 例えば 47-CA-GLY で回転させるとき、広い範囲で回転可能であり、コンフォーメーションが1つに決まらない。
このことは 何か別の物体が そのくぼみに挟まっている可能性を示唆している。
だいたいの部分はこのコンフォーメーションで おおむね安定である。
しかし グルカゴンは非常に小さなタンパク質のため、周囲を囲む他のタンパク質がくっついている部分なども考慮する必要がある。
(Fig.34) 異なった結合長は "分離した" 電子の存在による。

いずれにしろ、正確な電子分布を考慮することは 実際のタンパク質構造や作用の理解のためには 必要不可欠である。
このページに示したように、 O-F ( もしくは C-F, フッ素 ) と O-Cl ( もしくは C-Cl, 塩素 ) の結合長の違いは分離した電子による。
もし すべての電子が 原子核周囲を 滑らかに分布しているとしたら、それらの違いは Fig.5 に示したように なくなってしまう。
もちろん、タンパク質内で これらの分離した電子を使用するには、非常に曖昧な概念である量子力学の波動関数は 諦めなければならない。
---------------------------
もし 何かしらの分子模型を持たれているとしたら、これらのコンフォーメーション変化を容易に理解できる。
また このプログラム ( x-y, x-z, y-z 平面 ) を用いて 容易にこれらの分子模型を組み立てることができる。

2013/7/12 updated This site is link free.