しかし もし何もこれらの変数を固定しないと この理論はまったく役に立たない。
そのため 例えば 計量 g をデルタ関数を用いて固定する。
(Eq.1)
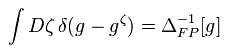
ここで ζ は ゲージパラメーターである。
トップページ (2電子原子も含む正確な新ボーア模型)
共形場理論とセントラルチャージは物理なのか ?
超ひも理論 vs. ループ量子重力理論。
経路積分法では、X、ゲージ、計量 g などの関連するすべての変数に関して積分をしなければならない (無限大から無限大)。
しかし もし何もこれらの変数を固定しないと この理論はまったく役に立たない。
そのため 例えば 計量 g をデルタ関数を用いて固定する。
(Eq.1)
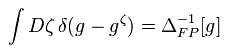
ここで ζ は ゲージパラメーターである。
ΔFP は デルタ関数の積分で生じる。
(Eq.2)

ΔFP を "FP-行列式" と呼ぶ。
Eq.1 から、 次を得る。
(Eq.3)
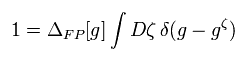
Eq.3 を 経路積分に代入して、g に関して積分すると、
(Eq.4)

Eq.4 から、 好みの 計量 g になる ゲージ ζ に固定できる。
(Eq.5)

このページ (Eq.4) のように、 計量 g が ゲージ変換で次のように変わるとする。
(Eq.6)

ここで ω は スケール変換である。
つまり、Eq.1 のゲージ固定は 次の表現に等しい。
(Eq.7)

計量の固定 = 計量の変分 (Eq.6) がゼロ = デルタ関数。
ここで 対称テンソル β (スカラー形成のため)を導入して この β が次を満たすとする。
(Eq.8)

これは β が 対称的かつトーレスレス (=トレース和がゼロ)であることを示している。
次のデルタ関数の定義を用いる。
(Eq.9)

Eq.8 と Eq.9 を用いて、 Eq.7 は次のように表せる。
(Eq.10)

ここで β は 汎関数で ( Eq.9 の p に相当する )、 ω は Eq.8 により消える。
Eq.5 に示すように、 逆数 でなく ΔFP が知りたい。
これをするには、 β や ε を 非常に奇妙な概念である "グラスマン数" に変える。
(Eq.11)

グラスマン数は フェルミ粒子のように反交換で 次を満たすとする。
(Eq.12)
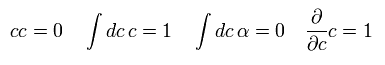
驚くことに グラスマン数では 微分が積分と同じなのである。
これはおかしいと言わざるを得ない。
Eq.11 を用いて、 Eq.10 は、
(Eq.13)
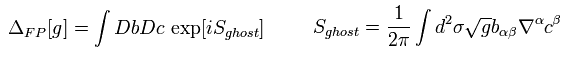
ここで 1/(2π) を相関関数の規格化のために導入した。
例え Eq.13 の係数を変えても、この変化はキャンセルされる。
( 相関関数とストレスエネルギーテンソルの係数が相殺する。)
X の係数 α の場合を参照のこと。( このページ (Eq.56, 59-61, 73, 74)。)
なぜなら Eq.10 は 次のように表せる。
(Eq.14)

また Eq.12 を用いて、
(Eq.15)

Eq.14 は Eq.15 の逆数である。
このセクションで示したように、これらの ゴースト や グラスマン数は単なる "数学上"の概念にすぎず、まさに "ゴースト" と言える。
次に 変数 ( x0 = 時間、 x1= 空間、ユークリッド ) を 次のように変換する。
(Eq.16)

かつ
(Eq.17)

(注意: ここの z と bar-z は このページのものとは違う。 )
Eq.17 では、空間変数 x1 の境界条件が 0 = 2π となる(=複素空間の円 )。
x0 = -∞ の時間 (= 無限の過去) のとき、 この複素平面の円の半径は ゼロ になる。
x0 = +∞ の無限の未来のとき、この円の半径は +無限大になる。
ネーターの定理によれば、 作用がある変換で不変 (= 対称 ) のとき、保存されるカレントと 電荷が存在する。
(Eq.18)

ここでは 空間は 1次元である。
Eq.18 と x1 の境界条件より、
(Eq.19)

つまり、全電荷 Q は 保存されている。
このページ (Eq.31)より、 この電流 J は ストレスエネルギーテンソル T に関係している。
(Eq.20)

空間積分は 複素平面の線積分を意味しており、Eq.18 と Eq.20 より、電荷 Q は、
(Eq.21)

Eq.21 の電荷 Q と、あるプライマリー場 φ の交換関係は 次のように表せる。
(Eq.22)

ここでは Q と φ は 時間順序に並んでいるとする ( 円の半径を用いて )。
ここでは 留数定理を用いている。
(Fig.1)

留数定理では、1/(z-a) の係数のみ残る。
(Eq.23)
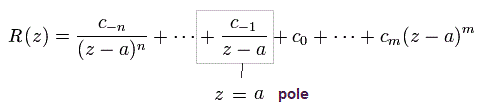 で
で
(Eq.24)
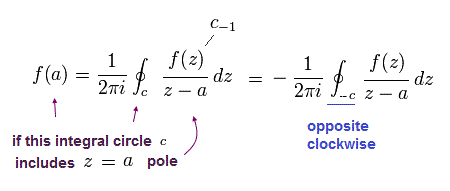
ストレスエネルギーテンソルと あるプライマリー場 φ の OPE を次のように仮定する。
(Eq.25)

Eq.22 の交換関係は、
(Eq.26)

ここでは 最初の項に部分積分を使用している。
このページ (Eq.36) に示したように、次の関係式を得ることができた。
(Eq.27)

つまり、この電荷 Q は 無限小変換の 生成子 を意味している。
( しかし 人為的な数学上の仮定が多い気がするが・・。 )
無限小変換 ε を次のように展開する。
(Eq.28)

これは ローレン展開である。
Eq.20 と Eq.21 から、電荷 Q を次のように定義する。
(Eq.29)

つまり、 L は、 ( z の項 )
(Eq.30)

この L は Virasoro 代数という。
このページ (Eq.74)、 Fig.1、 Eq.25 ( T の h は "2" )、 Eq.30 を用いて、 次を得る。
(Eq.31)

ここでは 部分積分と留数定理を使用している。.
最終的に次を得る。
(Eq.32)
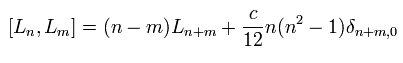
Eq.32 の "c" が ゼロでないと、 Eq.32 は 対称性 や 群論に関して美しくない。
だから 彼らは Eq.32 の電荷はゼロにならなければならないと主張している。
( また c がゼロでないと、Eq.25 から Eq.27 の生成子のルールが Eq.27 の φ が T のとき 破れてしまう。)
そのかわり、奇妙な 26 次元 ( もしくは 10 次元 ) の時空間を受け入れなければならない。
残念ながら、これらは単なる数学上の概念であり、リアリティーがない。
( 重要なのは 非対称と余剰次元 どっちが深刻か ということである。 )
このページ (Eq.56, Eq.83) に示したように、 スカラー場とゴーストのトータルの作用は、
(Eq.33)

ここでは 変換の違いを強調するため bar-X を採用している。
これらの変数が次のように変換すると仮定すると、
(Eq.34)

これは "BRST 変換" と呼ばれるものである。
作用 Eq.33 は Eq.34 の変換のもとで 不変である。
(Eq.35)

ここでは 次を使用している。
(Eq.36)

このように 彼らは 新たな数学上の変換をこしらえて、対称性のみを追及しているようにみえる。
しかし 最も重要な点は これらの対称性が 実際に この現実の世界とリンクしているかどうかということである。

2012/8/24 updated This site is link free.