トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは実在しない
我々の新しいボーア模型によって、ヘリウム原子の基底状態エネルギーの計算で、量子力学的な変分法よりも正確な結果をだすのに成功した。(トップページ参照のこと)。
この成功した新ボーア模型では、ヘリウム原子 (He) の2つの電子は、ちょうど1ド・ブロイ波長の互いに垂直な軌道上を運動している。
さらに、我々は炭素の4つの価電子と酸素の6つの価電子の運動のイメージ化に成功した。
(炭素のページ と 酸素のページ を参照のこと。)
このページ(メタンのビリアル定理)では、新しいボーア模型でメタン分子を表すのに成功した。
C-C 結合を考えるとき、我々はメタン分子の 2nd version も使う必要がある。
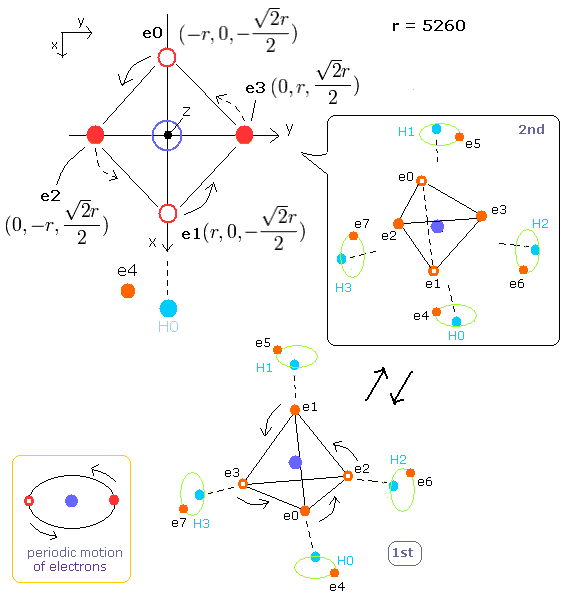
Fig. 1. メタン(CH4)分子の電子の周期運動。

炭素のページに示したように、炭素原子の4つの価電子が正四面体状に配置されるときは、2パターンある。
1st version --- 炭素の4つの電子が各水素原子核に最も近づくとき。
2nd version --- 炭素の4つの電子が核を挟んで元の位置から正反対に位置しているとき。
もちろん、1st と 2nd version のメタンの基底状態のエネルギーは同じである。(= -219.675 eV).
1st version のメタンでは、水素の電子は炭素の電子によって少し外側に追い出されている。
2nd version のメタンでは、炭素の電子が水素原子核から遠ざかったため、水素の電子は炭素原子核に少し近付いている。
(一方で、酸素原子の”正八面体”構造は1パターンしかない。)
ここでは、次のサンプル JAVA プログラムを使って 2nd version のメタンを表現してみることにする。
メタン (2nd version) のサンプル JAVA プログラム
中にあるプログラムをテキストエディタ(メモ帳など)にコピー & ペーストすれば、そのまま簡単にコンパイルして実行することができる。
(力の単位: 1000 = ボーア半径離れた +e の核と -e の電子の間にはたらく力の大きさ。)
ビリアル定理によれば、メタンの全位置エネルギー (tV) は、-219.675 × 2 = -439.3 eV となる。
全位置エネルギーが -439.3 eV のとき、メタンの8つの電子はどう配置されているのだろうか?
詳細な方法については、このページを参照のこと。
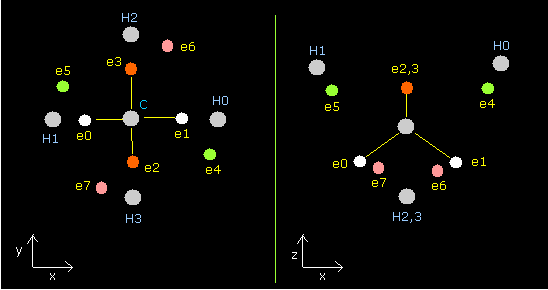
Fig. 2. 2nd version のメタン (CH4) の電子。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -5260 | 0 | -3719 | 6442 | 2107 | 0 | -12 | 0 | 2.007 |
| ele 1 | 5260 | 0 | -3719 | 6442 | 2107 | 0 | 12 | 0 | 2.007 |
| ele 2 | 0 | -5260 | 3719 | 6442 | 2107 | 12 | 0 | 0 | 2.007 |
| ele 3 | 0 | 5260 | 3719 | 6442 | 2107 | -12 | 0 | 0 | 2.007 |
| ele 4 | -838 | -3530 | -2000 | 4142 | 1574 | 328 | 6 | 208 | 1.000 |
| ele 5 | 837 | 3530 | -2000 | 4142 | 1574 | -328 | -6 | 208 | 1.000 |
| ele 6 | 3530 | -838 | 2000 | 4142 | 1574 | -6 | 328 | -208 | 1.000 |
| ele 7 | -3530 | 837 | 2000 | 4142 | 1574 | 6 | -328 | -208 | 1.000 |
Table 1 に示されるように、水素の電子 4-7 は各水素原子核にひきつけられている。
つまり、水素原子核もこれらの電子にひきつけられている。(Cn の値は大きい。)
このページにみられるように、電子 4-7 と 1st version のメタンの各水素原子核との距離は 4896 MM である。
つまり、平均距離 (nuc) は、( 4896 + 4142 ) / 2 = 4519 MM (約 4500 MM)である。
我々は、2nd version のメタンの電子配置を知ることができた。
エタンのすべての結合 ( 6 × C-H + C-C ) を切断するのに、2826.1 kJ/mol (= 29.29 eV) のエネルギーが必要である。
そのため、エタンの基底状態エネルギー (8つの炭素原子の価電子+6つの水素原子) は、-29.29 -148.024 × 2 -13.606 × 6 = -406.974 eV となる。
(148.024 eV は炭素原子の 1-4th のイオン化エネルギーの合計である。)
ビリアル定理によれば、全位置エネルギー (tV) は、2 × -406.974 = -813.948 eV である。
C-C と C-H 結合長は それぞれ 15351 MM と 10940 MMである。 (1 MM = 10-14 meter).
また C-C-H 角は 111.7°である。
Fig. 3. エタン (H3C-CH3) の電子の周期的な運動。
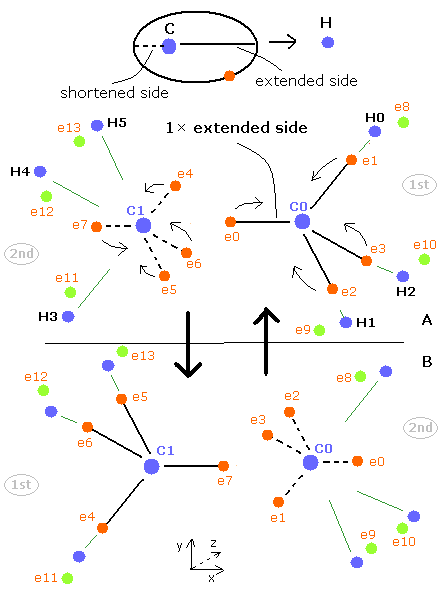
Fig.3 に示すように、エタン分子は 1st version と 2nd version のペアのメタンによって成り立っている。
2つの炭素原子核の間では、4つの電子が互いに避けながらもう一方の原子核にひきつけられている。
基本的に、各電子軌道は水素や他の炭素などの正の原子核によって引きのばされている。
しかし、ここではビリアル定理を使っているため、電子軌道の両サイドは平均的な長さになっている。
ここでは、次のサンプル JAVA プログラムを使ってエタン分子を表現してみることにする。
詳細については、このページを参照のこと。
エタンのサンプル JAVA プログラム (ビリアル定理)
(もし中のプログラムをテキストエディタ(メモ帳など)にそのままコピー & ペーストすれば簡単にコンパイルして実行できる。)
このプログラムでは、中心電荷 (+4e = +6e -2e) を +4.217 としている。
つまり、もし”四面体構造”が完全に保たれると、ド・ブロイ波はちょうど 2.000 となる。
Fig. 4. エタン (H3C-CH3) の電子配置。
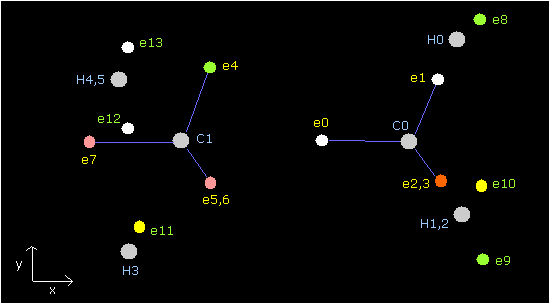
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6285 | 0 | 0 | 6285 | 1880 | 0 | 0 | 0 | 2.006 |
| ele 1 | 2305 | 6019 | 0 | 6445 | 1267 | -6 | 2 | 0 | 1.995 |
| ele 4 | 2235 | 6045 | 0 | 6444 | 2064 | 33 | -6 | -43 | 1.999 |
| ele 5 | 2235 | -3022 | -5235 | 6444 | 2064 | 33 | -34 | 27 | 1.999 |
| ele 6 | 2235 | -3022 | 5235 | 6444 | 2064 | 33 | 40 | 16 | 1.999 |
| ele 7 | -6360 | 0 | 0 | 6360 | 2116 | 0 | 0 | 0 | 2.006 |
| ele 8 | 1800 | 1825 | -3705 | 4505 | 1017 | -247 | -614 | -2 | 1.000 |
| ele 10 | 1800 | 2296 | 3432 | 4505 | 1017 | -247 | 309 | -530 | 1.000 |
| ele 11 | 800 | 1975 | 3900 | 4444 | 1416 | -172 | -298 | 0 | 1.000 |
Table 2 では、全位置エネルギーは -813.37 eV となり、これは実験値 -813.948eV とほぼ同じである。
電子 (8-13) と各水素原子核との平均距離は、(4505 + 4444) / 2 = 4474.5 MM, であり、これは ほぼ 4500 MM である。
もう一つの炭素の反発力のため、"正四面体"構造は少し壊れている。
ド・ブロイ波は 2.000 と少し異なる。(誤差は ± 0.005 ぐらいだ。)
次にスクロールバーの中から 16500 を選んで C-C (MM) ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6300 | 0 | 0 | 6300 | 2049 | 0 | 0 | 0 | 2.010 |
| ele 1 | 2315 | 6020 | 0 | 6449 | 1261 | -8 | 3 | 0 | 1.995 |
| ele 4 | 2290 | 6050 | 0 | 6468 | 2082 | 25 | -4 | -42 | 2.000 |
| ele 5 | 2290 | -3025 | -5239 | 6468 | 2082 | 25 | -34 | 25 | 2.000 |
| ele 6 | 2290 | -3024 | 5239 | 6468 | 2082 | 25 | 39 | 17 | 2.000 |
| ele 7 | -6380 | 0 | 0 | 6380 | 2119 | 0 | 0 | 0 | 2.016 |
| ele 8 | 1900 | 1600 | -3750 | 4498 | 1042 | -233 | -567 | -3 | 1.000 |
| ele 10 | 1900 | 2447 | 3260 | 4498 | 1042 | -233 | 287 | -489 | 1.000 |
| ele 11 | 800 | 1876 | 4110 | 4588 | 1358 | -158 | -234 | 1 | 1.000 |
基本的に、4つの核 (3つの水素原子核+他の炭素原子核) の反発力はつり合っており、炭素原子核は安定になる。
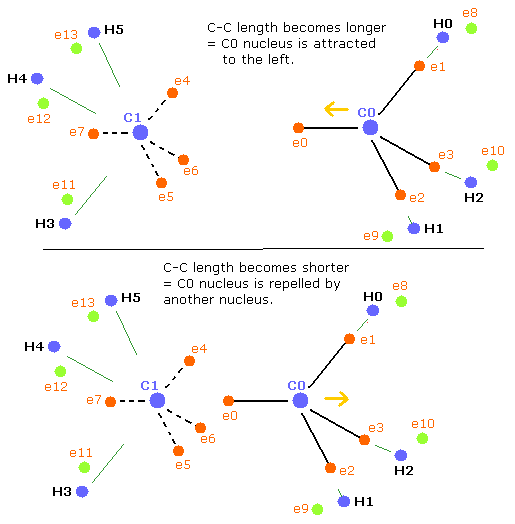
しかし、C-C 長がつりあいの長さよりも長くなると、他の炭素原子核の影響が弱くなる。(Fig.5 上)。
結果として、4つの反発力のバランスがくずれて、炭素原子核を安定化するためには (= C0,1 の FX,FY,FZ が小さくなる)、”正四面体”構造が より壊れてしまう。
Table 3 では、最大誤差が 0.016 であり、これは control の Table 2 よりも大きい。
また、全位置エネルギー (tV) は -806.74 eV であり、これは実験値 (-813.948 eV) よりも高い。
よって、Table 3 の C-C 結合は control よりも弱いことになる。
Fig. 5. エタン (H3C-CH3) の力のバランス。
次に、スクロールバーの中から、 14000 の値を選び、C-C (MM) ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6190 | 0 | 0 | 6190 | 1592 | 0 | 0 | 0 | 1.996 |
| ele 1 | 2350 | 6070 | 0 | 6509 | 1192 | -9 | 3 | 0 | 2.003 |
| ele 4 | 2235 | 6100 | 0 | 6496 | 1993 | 42 | -8 | -43 | 2.007 |
| ele 5 | 2235 | -3050 | -5282 | 6496 | 1993 | 42 | -33 | 29 | 2.007 |
| ele 6 | 2235 | -3049 | 5282 | 6496 | 1993 | 42 | 42 | 14 | 2.007 |
| ele 7 | -6280 | 0 | 0 | 6280 | 2188 | 0 | 0 | 0 | 1.991 |
| ele 8 | 1800 | 1825 | -3705 | 4505 | 1011 | -246 | -609 | -2 | 1.002 |
| ele 10 | 1800 | 2296 | 3432 | 4505 | 1011 | -246 | 307 | -526 | 1.002 |
| ele 11 | 800 | 1945 | 3800 | 4343 | 1470 | -174 | -327 | 0 | 0.999 |
C-C 長が つりあいのとれた長さよりも短くなると (Table 4 のように)、C0 原子核はもう1つの原子核によって反発力をより受けることになる。しかし一方で、C1 原子核は e0 電子により近づく。
つまり、C1 原子核は右に引き寄せられ、不安定になる。 (Fig.5 下)。
結果として、炭素原子核を安定にするために ( = C0,1 の FX,FY,FZ が小さくなる) は、”正四面体”構造がより壊れてしまう。
(Table 4 では、最大誤差が 0.009 であり、これは Table 2 の control よりも大きい。)
次にスクロールバーの中から 13500 を選び、C-C (MM) ボタンをクリックする。すると C-C の長さはさらに短くなる。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6180 | 0 | 0 | 6180 | 1354 | 0 | 0 | 0 | 1.987 |
| ele 1 | 2305 | 6095 | 0 | 6516 | 1190 | 2 | 0 | 0 | 2.007 |
| ele 4 | 2200 | 6200 | 0 | 6578 | 1934 | 55 | -10 | -46 | 2.024 |
| ele 5 | 2200 | -3100 | -5369 | 6578 | 1934 | 55 | -35 | 32 | 2.024 |
| ele 6 | 2200 | -3099 | 5369 | 6578 | 1934 | 55 | 45 | 14 | 2.024 |
| ele 7 | -6300 | 0 | 0 | 6300 | 2173 | 0 | 0 | 0 | 1.984 |
| ele 8 | 1800 | 1850 | -3680 | 4494 | 1011 | -247 | -623 | -1 | 1.000 |
| ele 10 | 1800 | 2261 | 3442 | 4494 | 1011 | -247 | 312 | -538 | 1.000 |
| ele 11 | 850 | 1980 | 3840 | 4403 | 1446 | -173 | -315 | 0 | 0.999 |
Table 5 では、C0 原子核は他の原子核によってさらに反発され、C1 原子核は e0 電子によってさらにひきよせられる。(Fig.5 下)
つまり、炭素原子核を安定にするには (= C0,1 の FX, FY, FZ が小さくなる)、"正四面体"構造が上の Table 4 のケースよりもさらに壊れる必要がある。
Table 5 では、最大誤差が 0.024 であり、これは Table 2 の control よりも大きい。
ここでは、水素の電子 11,12,13 は、 電子 8,9,10 よりも炭素原子核に、より近づくとしている。(Fig.3 上)
(そのため、ele11 の +X, +Y 座標は 正の数になる必要がある。)
しかし、ele 11 の +X を 負にしようとすると、nuc の値は短くなり、”平均の”nuc が 4500 MM よりも短くなる。
そのため、ele11 の +X, +Y は正にする必要がある。
エチレン (= エテン) のすべての結合を切断するのに ( 4 × C-H + C=C ) 2253.1 kJ/mol (= 23.35 eV) のエネルギーが必要である。
そのため、エチレンの基底状態のエネルギー (8つの炭素の価電子+4つの水素原子) は、-23.35 -148.024 × 2 -13.606 × 4 = -373.822 eV となる。
C=C と C-H 結合長は それぞれ、13390 MMと 10870 MM となる。(1 MM = 10-14 meter).
また、C=C-H 角は 121.3°である。
Fig. 6. エチレン (H2C=CH2) の電子。
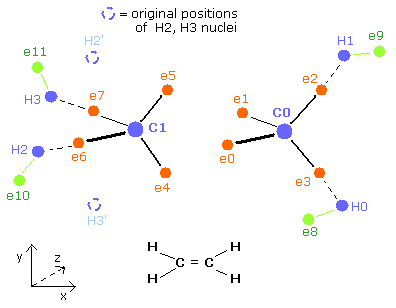
エチレンの分子も、1st と 2nd verision のメタンのペアで成り立っている。
炭素原子核間には、4つの電子があり、互いに避けながらもう一方の炭素原子核にひきよせられる。
エチレンには、1つ問題がある。
エチレンの場合は、C=C-H 角は 121.3°であり、これは エタンの C-C-H 角の 111.7°よりも大きい。
そのため、水素の電子が炭素原子核に与える影響を無視できなくなる。
8つの炭素の価電子と2つの水素原子核は 1st と 2nd version のメタンの両方において、”対称的に”配置されている。
しかし、水素の電子 (e8-e11) は”非対称に”配置されている。
(2nd version の e10,e11 は 1st version の e8,9 よりも 、Fig.2 に示すように炭素原子核に近づいている。)
そのため、2つの炭素原子核は 2nd version のメタンの方向に 交互に引き寄せられる。
結果として、水素の電子が炭素原子核に与える平均の力は ゼロになる。
実際の運動としては、Fig.6 において、e0,1 の (1st version) の軌道は e4,5 (2nd version) の軌道よりも長い (Fig 3 のように)。
そのため水素の電子の影響はつりあっている。
しかし、ここではビリアル定理をつかっており、楕円軌道の長いほうと短いほうの軌道を同じに仮定しており、この違いを区別できない。
そこで、水素の電子の力を平均化するために、”一時的に”Fig.6 に示すように 1st × 1st version のメタンを使うことにする。
各メタンの全エネルギーは同じだが、後で、水素原子核間の相互作用を少し補正する必要がある。
(もとのエチレンは全位置エネルギーにおいて、Fig.6 のエチレンよりも少し大きい (0.681 eV)。)
ここでは、次のサンプル JAVA プログラムを使ってエチレン分子を表現してみることにする。
詳細については、このページを参照のこと。
エチレンのサンプル JAVA プログラム (ビリアル定理)
(もし中のプログラムをテキストエディタ(メモ帳など)にそのままコピー & ペーストすれば簡単にコンパイルして実行できる。)
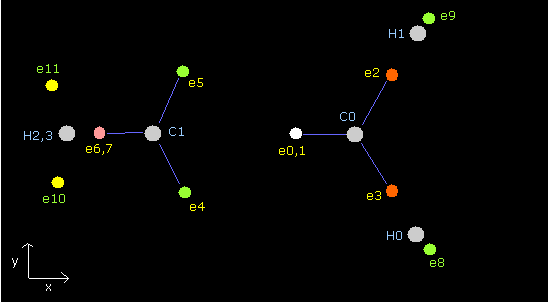
Fig. 7. エチレン (H2C=CH2) の電子配置。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -3869 | 0 | 5249 | 6520 | 2044 | -37 | 0 | -22 | 1.998 |
| ele 1 | -3869 | 0 | -5249 | 6520 | 2044 | -37 | 0 | 22 | 1.998 |
| ele 2 | 3500 | 5294 | 0 | 6346 | 1396 | 0 | 0 | 0 | 2.006 |
| ele 4 | 3750 | -5260 | 0 | 6459 | 2094 | 41 | 24 | 0 | 1.997 |
| ele 5 | 3750 | 5260 | 0 | 6459 | 2094 | 41 | -24 | 0 | 1.997 |
| ele 6 | -3568 | 0 | -5290 | 6380 | 1347 | 11 | 0 | -8 | 2.003 |
| ele 8 | 560 | -1100 | 4270 | 4444 | 1156 | -183 | 299 | 0 | 1.000 |
| ele 9 | 560 | 1100 | -4270 | 4444 | 1156 | -183 | -299 | 0 | 1.000 |
| ele 10 | -560 | -4280 | -1100 | 4454 | 1147 | 184 | 0 | 290 | 1.000 |
Table 6 では、全位置エネルギー (tV) は、-747.43 eV で、これは実験値 (-747.644 eV) とほぼ同じである。
次にスクロールバーの中から 15000 を選び、"C=C (MM)" ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -3910 | 0 | 5260 | 6554 | 2033 | -16 | 0 | -10 | 2.003 |
| ele 1 | -3910 | 0 | -5260 | 6554 | 2033 | -16 | 0 | 10 | 2.003 |
| ele 2 | 3490 | 5210 | 0 | 6270 | 1490 | -6 | 4 | 0 | 1.994 |
| ele 4 | 3770 | -5270 | 0 | 6479 | 2095 | 22 | 14 | 0 | 2.003 |
| ele 5 | 3770 | 5270 | 0 | 6479 | 2095 | 22 | -14 | 0 | 2.003 |
| ele 6 | -3590 | 0 | -5197 | 6316 | 1431 | 21 | 0 | -16 | 1.990 |
| ele 8 | 600 | -1100 | 4290 | 4469 | 1152 | -189 | 301 | 0 | 1.001 |
| ele 9 | 600 | 1100 | -4290 | 4469 | 1152 | -189 | -301 | 0 | 1.001 |
| ele 10 | -610 | -4290 | -1100 | 4470 | 1146 | 193 | 0 | 293 | 0.999 |
C=C の長さが 長くなると (Table 7)、炭素原子核の反発力が弱くなり、力のバランスがくずれる。
(これは Fig.5 の上のパネルと似ている。)
そのため、炭素原子核を安定にする (C0,1 の FX,FY,FZ を小さくする) ためには、”正四面体”構造がより崩れてしまう。
最大誤差は、0.010 となり、これは Table 6 の control よりも おおきい。
また、Table 7 では、全位置エネルギーが -717.74 eV となり、これは実験値 (=-747.644 eV) よりも高い。
そのため、Table 7 では結合の力が弱くなる。
次に、スクロールバーの中から 12500 を選び、"C=C (MM)" ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -3850 | 0 | 5200 | 6470 | 2078 | -53 | 0 | -30 | 1.988 |
| ele 1 | -3850 | 0 | -5200 | 6470 | 2078 | -53 | 0 | 30 | 1.988 |
| ele 2 | 3500 | 5350 | 0 | 6393 | 1331 | 5 | -3 | 0 | 2.015 |
| ele 4 | 3750 | -5240 | 0 | 6443 | 2106 | 57 | 31 | 0 | 1.995 |
| ele 5 | 3750 | 5240 | 0 | 6443 | 2106 | 57 | -31 | 0 | 1.995 |
| ele 6 | -3620 | 0 | -5350 | 6459 | 1249 | 13 | 0 | -10 | 2.015 |
| ele 8 | 560 | -1150 | 4265 | 4452 | 1145 | -185 | 308 | 0 | 1.000 |
| ele 9 | 560 | 1150 | -4265 | 4452 | 1145 | -185 | -308 | 0 | 1.000 |
| ele 10 | -560 | -4280 | -1100 | 4454 | 1138 | 183 | 0 | 286 | 1.001 |
C=C の長さが 短くなると (Table 8)、炭素原子核の反発力が強くなる。
(これは、Fig.5 の下のパネルのような場合だ。)
そのため、炭素原子核を安定にする (C0,1 の FX,FY,FZ を小さくする) ためには、”正四面体”構造がより崩れてしまう。
最大誤差は 0.015 で、これは Table 6 の control よりも大きい。
これらの結果は C=C の長さの 13390 MM がつりあいのとれた長さであることを示している。
アセチレン (HC ≡ CH) に関しては、このページを参照のこと。
アセチレンでは、炭素の電子はもう一方の炭素原子核に集中して引きつけられる傾向にあり、炭素の”正四面体”構造がエタンよりも,より崩れてしまう。
そのため、実際にアセチレンはとても不安定で他と反応しやすい。
酸素分子の O=O 結合を切断するのには、498 kJ/mol (= 5.16 eV) のエネルギーが必要である。
そのため、酸素分子の基底状態エネルギー (12個の酸素の価電子) は、-5.16 -433.103 × 2 = -871.366 eV となる。
(-433.103 eV は、酸素原子の 1-6th のイオン化エネルギーである。)
ビリアル定理によれば、全位置エネルギー (tV) は、 2 × -871.366 = -1742.732 eV となる。
また、O=O の長さは、12074 MM となる。
Fig. 8. 酸素分子 (O=O) の電子。
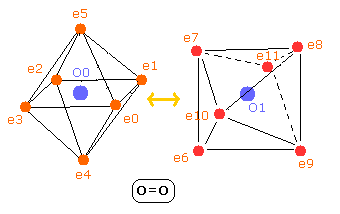
酸素分子では、2つの”正八面体”の酸素原子がクーロン力で互いにつながっていると考えられる。
(1つは、Fig.8 に示すように 90°回転している。酸素原子はすでに核を挟んで正反対のところに電子を持つ。)
我々は、この酸素分子を表現するのに次のサンプル JAVA プログラムを使う。
酸素分子のサンプル JAVA プログラム (ビリアル定理)
(もし中のプログラムをテキストエディタ(メモ帳など)にそのままコピー & ペーストすれば簡単にコンパイルして実行できる。)
このプログラムでは、中心電荷 (+6e = +8e -2e) を +6.271 としている。そのため、ド・ブロイ波はちょうど 2.000 となる。
Fig. 9. 酸素分子 (O=O) の電子。
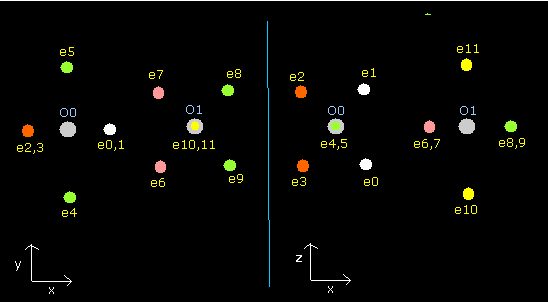
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3295 | 0 | -3165 | 4568 | 5832 | 0 | 0 | 0 | 1.985 |
| ele 1 | 3295 | 0 | 3165 | 4568 | 5832 | 0 | 0 | 0 | 1.985 |
| ele 2 | -3200 | 0 | 3260 | 4568 | 6004 | -4 | 0 | -4 | 2.002 |
| ele 4 | 10 | -4580 | 0 | 4580 | 5958 | -18 | 0 | 0 | 1.998 |
| ele 6 | -3295 | -3165 | 0 | 4568 | 5832 | 0 | 0 | 0 | 1.985 |
| ele 8 | 3200 | 3260 | 0 | 4568 | 6004 | 4 | -4 | 0 | 2.002 |
| ele 9 | 3200 | -3260 | 0 | 4568 | 6004 | 4 | 4 | 0 | 2.001 |
| ele 10 | -10 | 0 | -4580 | 4580 | 5958 | 18 | 0 | 0 | 1.998 |
| ele 11 | -10 | 0 | 4580 | 4580 | 5958 | 18 | 0 | 0 | 1.998 |
Table 9 では、全位置エネルギー (tV) は、-1741.3 eV であり、これは実験値 (-1742.732 eV) とほぼ同じである。
酸素原子核の電荷は炭素よりも大きい、そのため、ド・ブロイ波は炭素の場合よりも 不安定になる。
次に、スクロールバーの中から、"13000" を選び、"O=O (MM)" ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3295 | 0 | -3178 | 4577 | 5848 | -6 | 0 | -6 | 1.988 |
| ele 1 | 3295 | 0 | 3178 | 4577 | 5848 | -6 | 0 | 6 | 1.988 |
| ele 2 | -3200 | 0 | 3263 | 4570 | 5997 | -5 | 0 | -5 | 2.001 |
| ele 4 | 5 | -4584 | 0 | 4584 | 5943 | -13 | 0 | 0 | 1.998 |
| ele 6 | -3295 | -3178 | 0 | 4577 | 5848 | 6 | -6 | 0 | 1.988 |
| ele 8 | 3200 | 3263 | 0 | 4570 | 5997 | 5 | -5 | 0 | 2.001 |
| ele 9 | 3200 | -3263 | 0 | 4570 | 5997 | 5 | 5 | 0 | 2.001 |
| ele 10 | -5 | 0 | -4584 | 4584 | 5943 | 13 | 0 | 0 | 1.998 |
| ele 11 | -5 | 0 | 4584 | 4584 | 5943 | 13 | 0 | 0 | 1.998 |
O=O の長さが 長くなる (Table 10) と、酸素原子核間の反発力が弱くなる。
しかし、Table 10 では、全位置エネルギーが -1738.93 eV となり、これは 実験値 (= -1742.732 eV ) よりも高くなる。
つまり、Table 10 では、結合力が弱くなることを意味する。
次に、スクロールバーから 11000 を選び、"O=O (MM)" ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 3295 | 0 | -3154 | 4561 | 5777 | 20 | 0 | 19 | 1.981 |
| ele 1 | 3295 | 0 | 3154 | 4561 | 5777 | 20 | 0 | -19 | 1.981 |
| ele 2 | -3195 | 0 | 3269 | 4571 | 5999 | -7 | 0 | -7 | 2.004 |
| ele 4 | 15 | -4582 | 0 | 4582 | 5960 | -27 | 0 | 0 | 1.998 |
| ele 6 | -3295 | -3154 | 0 | 4561 | 5777 | -20 | 19 | 0 | 1.981 |
| ele 8 | 3195 | 3269 | 0 | 4571 | 5999 | 7 | -7 | 0 | 2.004 |
| ele 9 | 3195 | -3269 | 0 | 4571 | 5999 | 7 | 7 | 0 | 2.004 |
| ele 10 | -15 | 0 | -4582 | 4582 | 5960 | 27 | 0 | 0 | 1.998 |
| ele 11 | -15 | 0 | 4582 | 4582 | 5960 | 27 | 0 | 0 | 1.998 |
O=O の長さが短くなると (Table 11)、酸素原子核の反発力が 強くなる。
そのため、酸素原子核を安定にする (= O0,1 の FX,FY,FZ を小さくする) のに酸素の”正八面体”構造が より崩れてしまう。
最大誤差は 0.019 であり、これは Table 9 のコントロールのよりも大きい。
酸素分子は、H2O に比べて より不安定で反応しやすい。
この O2 の性質は、Table 9 の不安定なド・ブロイ波の値によって説明できる。

2010/12/8 updated This site is link free.