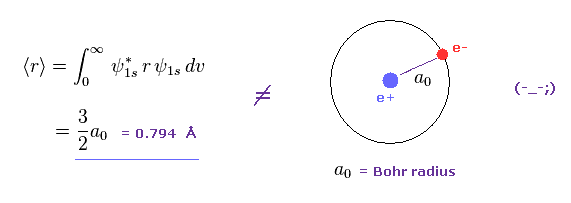
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは現実には存在しない。
特殊相対論は間違い。
(Fig.1) 量子力学の水素原子の軌道半径 ?
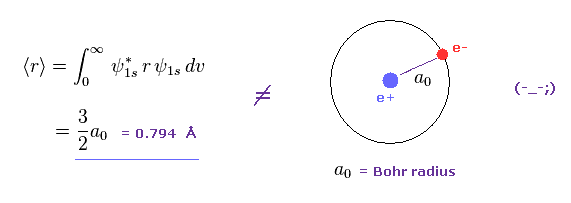
Fig.1 に示すように、もし シュレディンガーの水素の平均の軌道半径を計算すると、その値は 約 1.5 × ボーア半径になる。
この結果は ビリアル定理から得られたものと異なる。
(Fig.2) 水素原子のビリアル定理 → ボーア半径。
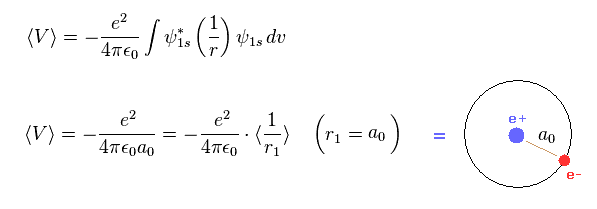
このページに示したように、シュレディンガーの水素は ビリアル定理を満たし、 その半径は 古典的な ボーア模型のように ボーア半径になる。
これはつまり ハートリー・フォック法による原子半径は ビリアル定理と一致しない。
この不一致は 量子力学的な模型の 非現実的な確率密度の広がりに起因する。
1s の水素の波動関数においても、ボーア半径における確率密度は最大になる。
しかし それらの平均値は ボーア半径と異なる。
(Fig.3) 水素のビリアル定理 → ボーア半径。

2つの同じ種類の原子が 中性の分子で 単一の結合を形成するとき、その結合長の 半分を 共有結合半径と呼ぶ。
例えば、H2 分子の核間距離は 0.74 Å であるため、水素の原子半径は 0.74 × 0.5 = 0.37 Å となる。
これらの共有結合半径は 実験そのものから得られたもので 量子力学的手法による軌道半径とは 何の関係もない。
実際に Fig.3 に示したように、量子力学的手法による軌道半径は 実際の原子半径とは 完全に異なる。
(Fig.4) 水素とヘリウムの原子半径。
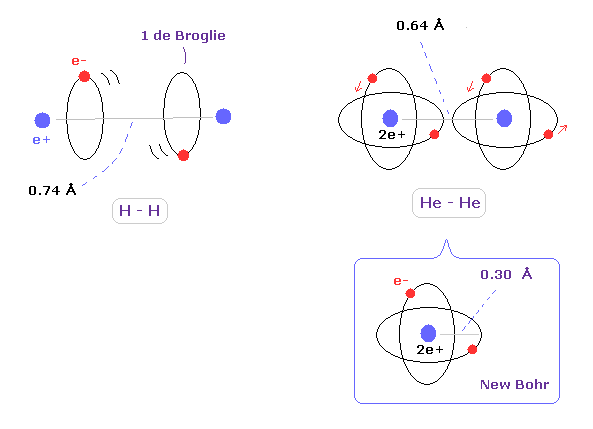
実際に 共有結合半径と 分子結合の実験値について考慮するとき、その分子の 具体的な外形は 非常に重要である。
例えば、水素分子 (H2) では、水素原子の2つの軌道は それらの エネルギー的に安定な状態を考えると 互いに ほぼ平行である必要がある。
つまり 単純に 2 × 原子半径が H2 分子の結合長にならないことになる。
このページに示したように、H2 分子において クーロン と ドブロイの関係式を用いて H2 分子の正確なエネルギー値を得ることができた。
一方で 量子力学的な模型は はっきりとした実在的な原子像をまったく示すことができない。
ヘリウム原子においては、 新しいボーア模型のヘリウムを用いた原子軌道半径 (= 0.30 Å ) は 実験値の共有結合半径と ほぼ同じ (= 0.32 Å ) である。
この一致は 実際のヘリウムの外形であることを示している。
(Fig.5) エタンの分子模型。
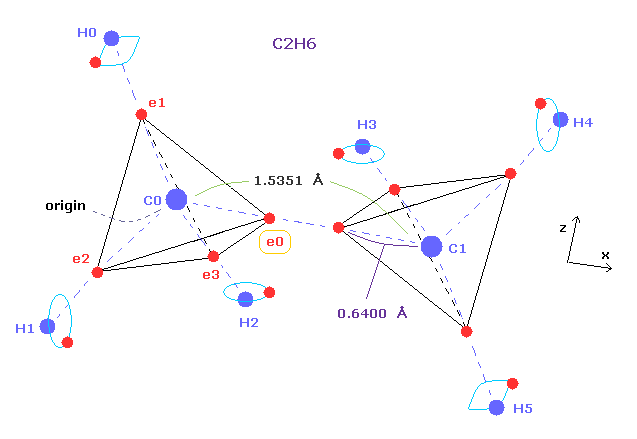
単一の C-C 結合長は 1.54 Å であるため、共有結合半径は 1.54 × 0.5 = 7.7 Åということになる。
しかし このページや このページに示したように、炭素の価電子の本当の回転軌道半径は クーロンとドブロイの関係式を考慮すると 0.64 Å (= 0.6400 × 10-10 meter ) である。
この値 0.64 は 7.7 よりも少し小さい。
つまり 共有結合半径 (= 0.77 ) 自体は 本当の原子半径 (= 0.64 ) を意味していない。
このページでは ボーア軌道( ドブロイ波長 )をベースとした手法が 電気陰性度などの実験結果と 良く一致することを示す。
(Fig.A-1) σ 結合 = 2つの電子がペアで 2つの H 原子間を行き来している?
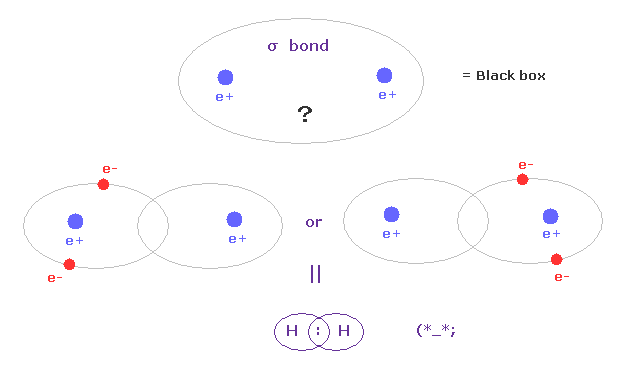
量子力学とパウリの排他原理によれば、互いに反対方向のスピンを持つ2つの電子が 1つの軌道に入ったとき、それらは安定すると彼らは主張している。
つまり σ 結合では、2つの電子は 1つの塊として 左右の水素原子のどちらかの 閉じた 1s 軌道に属するということになる。
これはつまり この2つの電子は 2つの H 原子間を 常にペアを組んで往来していることを示しているのだろうか?
残念ながら、各 H 原子核は 同時に 2つの負電荷の電子を引き付ける力はない。
つまり このパウリの排他原理と閉じた軌道に基づいた考えは クーロン相互作用の基本に従わない非実在的なものと言える。
(Fig.A-2) C-C 結合 = 2つの電子が行き来している ?
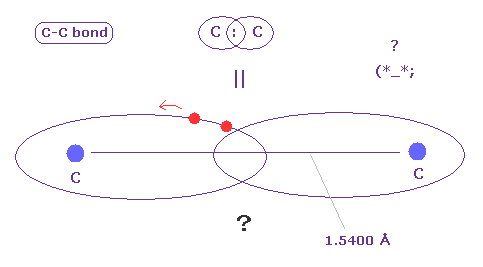
C-C 結合は 非常に長い (= 1.5400 Å )。
この 非常に長い結合長にも関わらず、2つの電子は パウリの排他原理を満たすために必ず ペアを形成しなければ ならないのだろうか?
現実的なクーロン相互作用を考慮すれば、各電子は どちらか一方の各炭素原子核に属し、それらがペアとしてかたまっていないと考えるのが自然である ( Fig.7 参照のこと )。
重要な点は 量子力学は 分子結合内のどこに電子が存在しているのか 具体的に答えることができないということである。
それらは まるで "ブラックボックス" のようである。
そのため 量子力学的な分子結合は 具体的な情報を何も提供できず、もっと大きな分子について考える場合 完全に役に立たないのである。
(Fig.A-3) 量子力学では 電子は球状に広がっている?
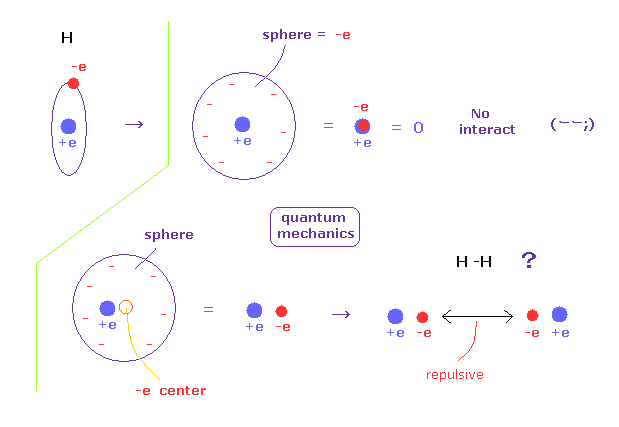
量子力学によれば、私たちは 水素原子内で 単一電子の場所を指定できない。
そのため、量子力学の単一電子は 必ず 波動関数として広がっていなければならない。
例えば 単一電子が 球状に広がっているとすると、そのポテンシャルエネルギーの観点からは その電子が 球の中心にあると見なせる。
もし 電子が中心にあるとしたら、それはちょうど +e の原子核と重なっており、水素原子は完全に中性になってしまう。
すると 水素原子は 他の原子とまったく相互作用できないことになる。
他の原子と相互作用するには 水素原子の電子は ボーア模型のように ある場所に局在化している必要がある。
(Fig.A-4) H-H 結合 = 2つの電子が互いに避け合っている。
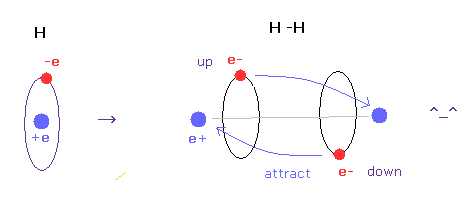
水素分子では、2つの電子が他の原子核に引きつけられている。
しかし もしこの状態を 球状の波動関数を用いて表そうとすると、Fig.A-3 下図に示すように それらは互いに反発し合うことになる。
一方で 古典軌道を用いると、水素分子を自然に表すことができる。
この自然な模型では、2つの電子が互いに避け合って (= up と down )、他の原子核にひきつけられて 共有結合を形成する。
結果的に 共有結合を表すには 様々な分子において 具体的に局在化した電子を用いる必要がある。
電気陰性度 ( Pauling ) は 分子内で 負電荷の電子を引きつける力を意味している。
この 電気陰性度は 様々な結合エネルギーの実験値を比較して得られた平均値である。
水素原子 (H) の 電気陰性度は 2.20 であり、 炭素 (C) のは 2.55 である。
つまり H と C 原子の 電子を引きつける力は ほぼ同じということになる。
(Fig.6) メタンにおける 価電子 (= e0 ) に作用する "Force 1"。
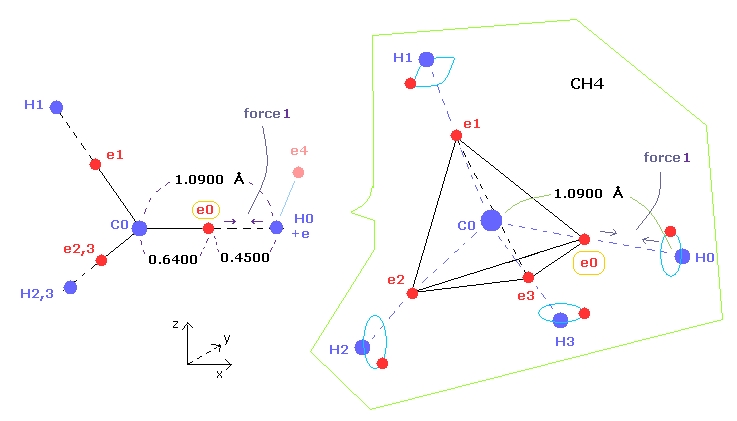
このページや このページ (Fig.22)に示したように、炭素の4つの価電子の回転半径は 1-4 の全イオン化エネルギーと "2" ドブロイ波長の軌道を考慮すると、約 0.6400 × 10-10 meter,となる。
結果的に 価電子 e0 が 水素原子核に最も近づいたとき、それらの距離は 1.0900 (= C-H ) - 0.6400 により 0.4500 Å となる。
この地点において ( クーロン力の ) "force 1" が 炭素の価電子 e0 と H0 原子核間に働いている。
(Fig.7) エタン ( CH3-CH3 ) の周期的な運動。
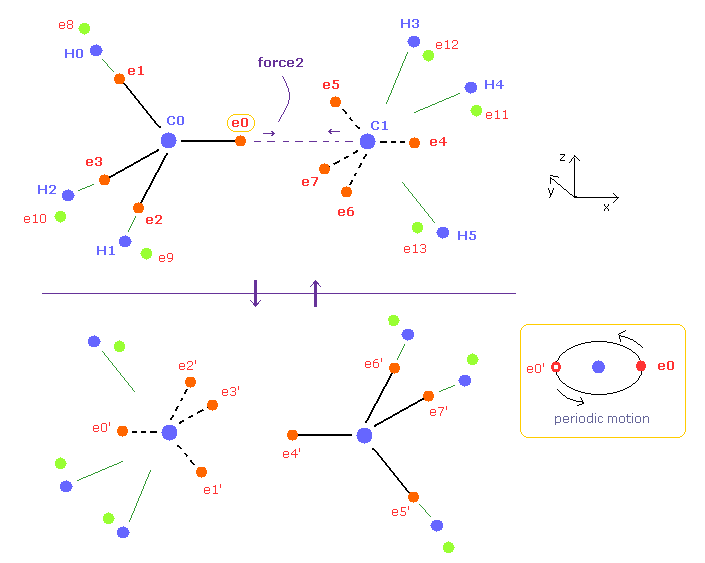
炭素の4つの価電子は それらの対称的な分布を考慮すると 正四面体状に分布している。
各電子は 実際に 各炭素原子核周囲を回っているので エタンでは Fig.7 の上下のパターンを周期的に繰り返していると考えられる。( このページも参照のこと。 )
(Fig.8) エタンの価電子 (= e0 ) に作用する力 "force 2"。
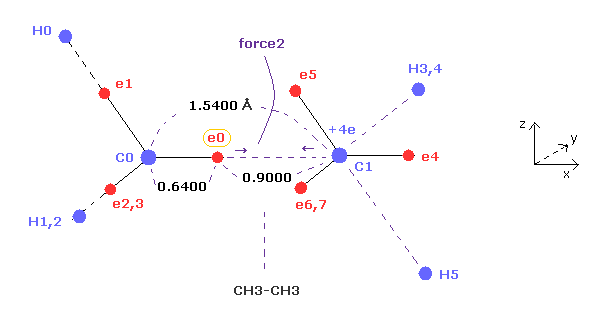
Fig.8 は Fig.7 のエタンの x-z 断面図である。
エタンの C-C 結合長は 1.5400 Åで、価電子 e0 と C0 原子核間の距離は メタンのときのように "2" ドブロイ波長の軌道を考慮すると、 約 0.6400 Åである。
結果的に e0 と 他の炭素原子核 C1 の距離は 約 0.9000 Å (= 1.5400 - 0.6400 ) である。
また 2つの 1s 電子の効果を +6e の炭素原子核から差し引いいて 炭素 (= C1 ) の中心電荷は 約 +4e である。
"Force 2" は この e0 電子と C1 原子核間に働く力である
(Fig.9) メタンとエタンにおける クーロン力 1、 2 は ほぼ同じである。
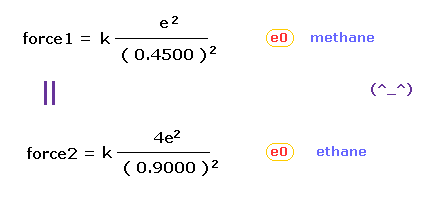
Fig.6 (= メタン ) と Fig.8 (= エタン ) から、 e0 の価電子と 他の原子核 ( H0 もしくは C1 原子核 ) 間に働く力を知ることができる。
クーロンの逆二乗の法則を使用すると、メタンの "force 1" は エタンの "force 2" にほぼ等しくなる。
この結果は H と C 原子核の ほぼ同じ電気陰性度に一致する。
また Fig.9 の結果は メタンとエタンの両方において クーロンとドブロイ波長の関係が 非常に重要であることを示している。
このセクションでは、クーロンとドブロイの関係式に基づいた 炭素様原子 (= C, Si ) の 真の原子半径を得る方法について詳しく一度説明する。
(Fig.10) 炭素様原子の正四面体構造。
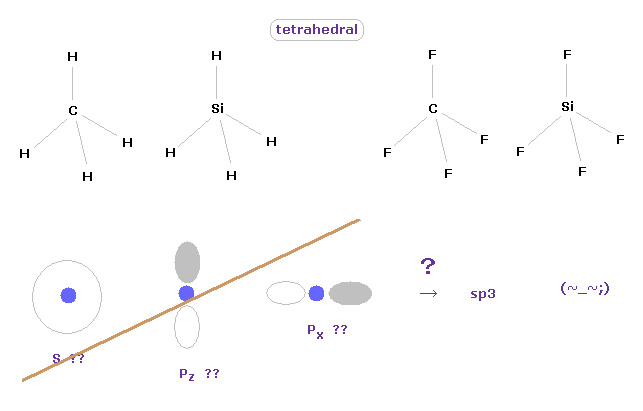
炭素様原子の 4つの価電子の対称的な構造を考慮すると、それらの4つの電子は 原子核周囲に 正四面体状に分布しているのは自然なことである。
実際に メタン (= CH4 )、4フッ化メタン (= CF4 )、シラン (= SiH4 )、4フッ化ケイ素 (= SiF4 ) は 正四面体構造であることが知られている。
これはつまり 量子力学の "s" や "p" 軌道の概念が まったく役にたたず かつ 非実在であることを意味している。
彼らは "sp3" という新しい概念をこしらえようとしているが、この操作は 非常に人為的なものである。
これらの "s"、"p"、"d" などの 非実在的な電子分布は 現実的かつ明白な像で 様々な分子軌道を表すことを阻害している。
(Fig.11) 炭素様原子の価電子。
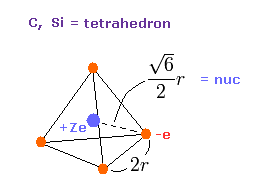
ここで Fig.11 価電子の分布を用いて、"実在的"な原子半径と 中心電荷 Z を計算する。
正四面体 ( Fig.11 ) の 1辺の長さを "2r" とする。
全ポテンシャルエネルギー V は +Ze の原子核と電子間の 引きつける V と 4つの価電子間の 反発 V の合計である。
(Eq.1) 全ポテンシャルエネルギー V。
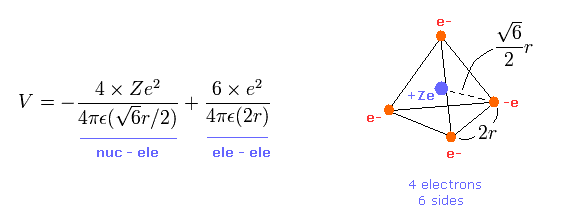
Eq.1 の最初の項は Ze の原子核と 各電子間のポテンシャルエネルギーである。
また 2項目は 4つの価電子間の反発ポテンシャルエネルギーである。
正四面体は 6つの辺をもつため 電子間の 6つの相互作用がある。
(Eq.2) 全運動エネルギー T。
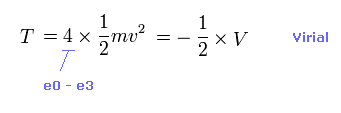
全運動エネルギーは 4つの価電子の運動エネルギーの合計である。
ビリアル定理を用いて、 この T を 全ポテンシャルエネルギー V から得ることができる ( T = -1/2 V = -E )。
Eq.2 の関係式から、各電子の速度 "v" と ドブロイ波長 (= h/mv ) を得ることができる。
(Eq.3) 各電子に作用する 力 F。
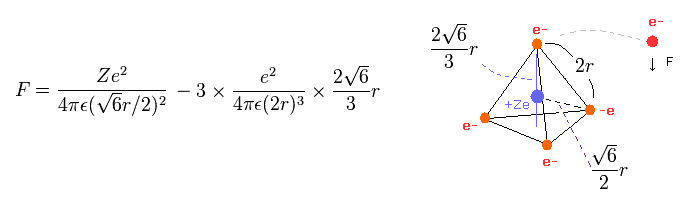
Eq.3 は 各電子に作用する 力 F を表している。
Eq.3 の最初の項は 原子核による引力である。
2番目の項は 他の3つの電子からの反発力である。
T からの 上記の速度 (v) と 力 F を用いて、遠心力が 力 (F) に等しいとする。
(Eq.4)
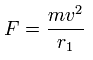
この r1 は この関係式で現れる "仮の" 半径である。
この r1 を用いて、1軌道に含まれる ドブロイ波 (= wn ) の数を得ることができる。
(Eq.5)
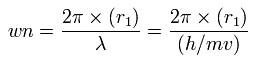
サンプル JAVA プログラム ( 原子半径 )。
C 言語プログラム ( 原子半径 ).
このサンプルプログラムでは、実行すると、最初に 原子の種類を選ぶ。
炭素様原子 (= C, Si ) を計算するときは 最初に "0" の数値を入力するように。
もし 酸素様原子 (= O, Si )、ホウ素様原子 (= B, Al ) を計算するときは それぞれ "1" もしくは "2" を入力するように。
次に 中心電荷 Z と すべての価電子の全イオン化エネルギーを入力する。
これらの値から このプログラムは 正四面体状の炭素のポテンシャルエネルギーと力を計算する。
ビリアル定理 ( E = -T = 1/2 V ) を用いて、このプログラムは 1軌道に含まれるドブロイ波を計算する。
画面上には このドブロイ波の数 (= 約 2.0 ) と、各価電子と中心の原子核間の距離 (MM) が表示される。
| 原子名 | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| 炭素 (C) | 11.260 | 24.383 | 47.888 | 64.494 | - | - | - |
| ケイ素 (Si) | 8.151 | 16.346 | 33.493 | 45.142 | - | - | - |
例えば、炭素の 1-4 のイオン化エネルギーの合計は 148.025 eV である。
Z = +4.0 のとき、 この wn は 1.87 ( 約 1.9) で 回転半径は 約 6000 MM になる。 ( 1 MM = 10-14 meter. )
また Z = +4.22 のとき、この wn は ちょうど 2.00 になり、その回転半径は 約 6400 MM になる。
この 4.0 と 4.22 の間の少しの差は 2つの 内殻の 1s の電子が +6e の炭素原子核から 離れていることによる。
また この結果は 4つの価電子の実際の動きを計算した下のプログラムから得られた結果と一致している。
サンプル JAVA プログラム -- 炭素の4つの価電子の視覚化 ( 中心電荷 +4.22。 )
上記のプログラム実行後、スクロールバーの中から "1.0" もしくは "2.0" のドブロイ波を選択して "orbit" ボタンをクリックすれば、 Z = 4.22 のとき、1軌道が ちょうど 2.0 ドブロイ波長のとき、その回転半径 (= nuc ) が 約 6400 MM (= 0.6400 × 10-10 meter. ) になる。
このページも参照のこと。
(Fig.12) 炭素 ( C ) の本当の原子半径。
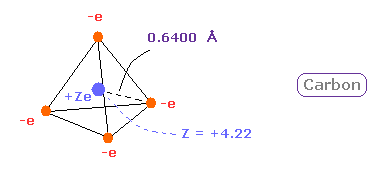
よって 炭素の本当の原子半径を 0.6400 Å、中心の正電荷を +4.22 と定義できる。
後で述べるように、これらの結果は 結合長と電気陰性度の実験結果に非常によく一致する。
次に ケイ素 ( Si ) の 1-4 のイオン化エネルギーの合計は 103.132 eV である。
ケイ素の外殻電子の軌道は n =3 ( 3 ドブロイ波長 ) のため、この値は n=2 の 炭素 (= 148.025 ) のときより小さい。
上記のプログラム実行後、同じように "0" (= 炭素様原子 ) を選択する。
そして Z = +5.05 のとき、1軌道のドブロイ波が ちょうど 3.00 で、その回転半径は ほぼ 1.1500 Åになる。
(Fig.13) ケイ素 ( Si ) の本当の原子半径。
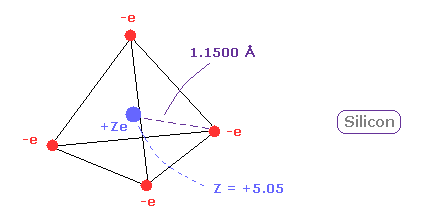
ケイ素 (Si) の原子半径は "3" ドブロイ波長のため 炭素よりも小さい。
実際に Si-H 結合長は 1.4800 Åで、 これは C-H 結合長 (= 1.0900 Å ) より長い。
また n=2 の中間の8つの電子が 広く分布しているため、 中心の正電荷 (= +5.05 ) は +4 よりも大きい。
(Fig.14) ケイ素 ( Si ) の長い原子半径 → 不安定。
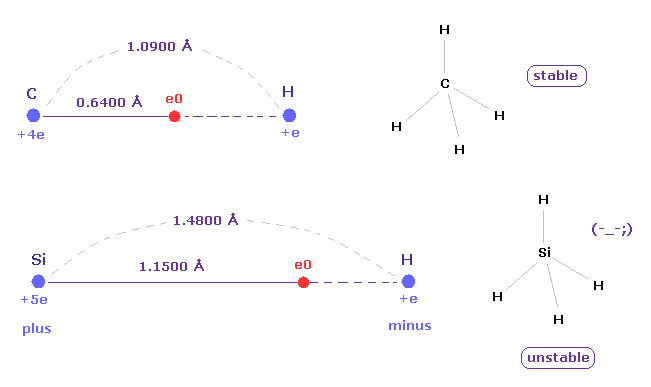
シラン (= SiH4 ) では、電気陰性度の違いにより 水素原子は 部分的に 負の電荷を持ち、ケイ素は 正の電荷を持つ。
この性質は ドブロイ波長をベースとした 新しい原子半径を用いれば 容易に理解できる。
Si と その価電子 e0 の間の距離は e0 と水素原子核間の距離より長いため、水素は負になりやすい。
Si-H の長い距離と ケイ素の弱い引力のため、シラン (= SiH4 ) は メタン (= CH4 ) よりも 不安定になりやすい。
また シランの気体は 空気中で 点火せずとも 自然発火する傾向にある。
(Fig.15) 新しい原子半径は Si-Si 結合長を説明できる、
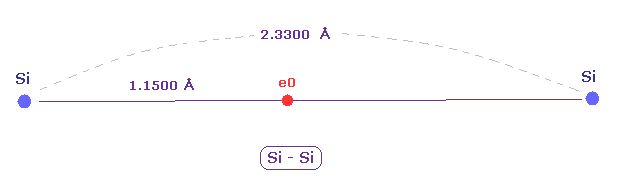
単一の Si-Si 結合長は 2.3300 Åである。
ドブロイ波長をベースとした 新しい原子半径は 1.1500 Åである。
2 × 1.1500 = 2.3000 は 実験値f 2.3300 Å に近い。
つまり 実際の値に近い結果をだせた。
(Fig.16) 酸素様原子 + 水素。
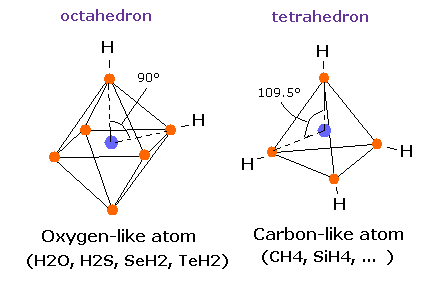
酸素様原子 (= O, S, Se, Te ) は 6つの価電子を持つ。
そのため これらの6つの電子は クーロン反発力を考慮すると、正八面体状に分布していると考えるのが自然である。
実際に H-S-H、 H-Se-H、H-Te-H の角度は それぞれ 92.1°、 91.0°、 89.5° である。 ( = ほぼ 90°)。
酸素のケースでは、水素原子が 他の原子より 酸素原子核に近づいているため、水素原子核による反発力が強くなり、水分子 (H2O) が O 原子核を安定に保つため 正八面体を保てなくなる。
(Fig.17) 6フッ化硫黄 SF6 = 正八面体。
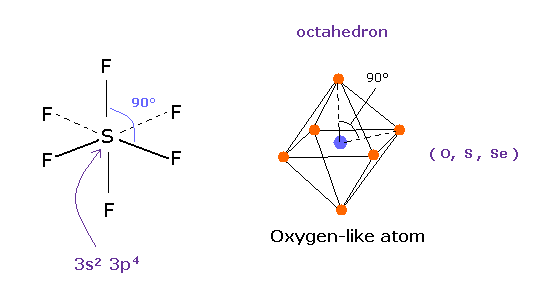
量子力学によれば、硫黄 (S) は 酸素原子のように 6つの価電子をもつ。
( 3s × 2 + 3p × 4 = 6. )
そして 安定な 六フッ化硫黄は ちょうど 正八面体構造を持ち、その F-S-F 角は ちょうど 90°である。
この結果は 明らかに 量子力学が主張する 3s2 3p4 状態が 間違いであり、対称的なクーロン反発力が ここで有効であることを示している。
(Fig.18) 酸素様原子の構造。
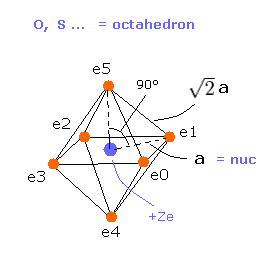
ここで Fig.18 の正八面体構造を用いて 酸素様原子の 本当の原子半径を計算する。
電子と原子核間のクーロン相互作用を考慮すれば、全エネルギー V は
(Eq.6) 全ポテンシャルエネルギー。
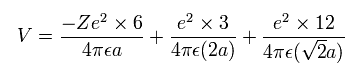
Eq.6 では、最初の項は Fig.18 における +Ze 原子核と 6つの電子間のポテンシャルエネルギーである。
(Eq.7) 全運動エネルギー。
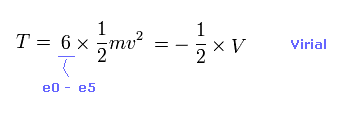
ビリアル定理 ( T = -1/2 V ) を用いると、全運動エネルギーと 各電子の速度 "v"、 ドブロイ波長 (= h/mv ) を知ることができる。
全運動エネルギーは 6つの電子の合計である。
(Eq.8) 各電子に作用する 力 F。
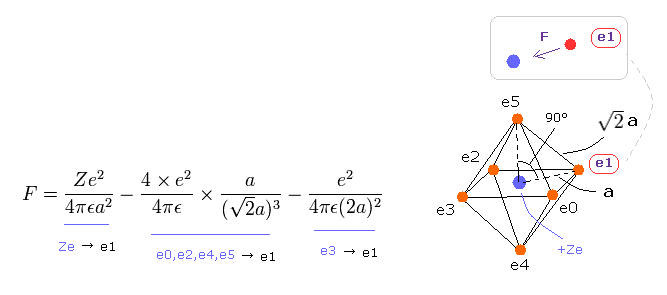
Eq.8 の F は 電子 "e1" に作用する全力である。
Eq.8 の最初の項は +Ze 原子核による引力である。
2番目の項は e0、 e2、 e4、 e5 からの、 3番目の項は e3 からの反発力である。
炭素様原子のように、Eq.4 と Eq.5 を用いて、1軌道内の ドブロイ波を知ることができる。
サンプル JAVA プログラム ( 原子半径 )。
C 言語プログラム ( 原子半径 ).
酸素様原子 (= O、S ) を計算するときは、最初に "1" の値を入力するように。
次に 中心の電荷 Z と 1-6 のトータルのイオン化エネルギーを入力する。
これらの入力値から、このプログラムは 正八面体構造の ポテンシャルエネルギーと力を Eq.6 - Eq.8、 Eq.4 - Eq.5 を用いて計算する。
画面上には このドブロイ波の数と、電子と原子核間の距離がでる。
| 原子名 | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| 酸素 (O) | 13.618 | 35.121 | 54.936 | 77.413 | 113.899 | 138.120 | - |
| 硫黄 (S) | 10.360 | 23.338 | 34.790 | 47.222 | 72.595 | 88.053 | - |
酸素の 1-6 の イオン化エネルギーは 433.107 eV である。
Z = +6.0 のとき、 この wn は 1.88 (約 1.9) になり、回転半径は 4300 MM. ( 1 MM = 10-14 meter. ) になる。
そして Z = +6.273 のとき、この wn は ちょうど 2.00 になり、回転半径は 約 4600 MM になる。
(Fig.19) 本当の酸素の原子半径。
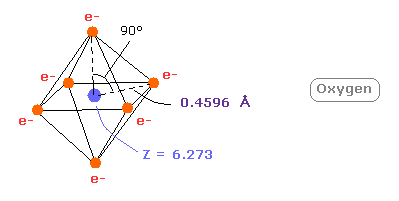
6.0 と 6.273 の間の小さな違いは 2つの内殻の 1s 電子が +8e の酸素原子核から離れていることによる。
( この影響は 5th と 6th のイオン化エネルギーに顕著である。 )
これらの値は 実験の現象と一致する。
(Fig.20) O-H と O-C 結合における クーロン力 1 と 2。
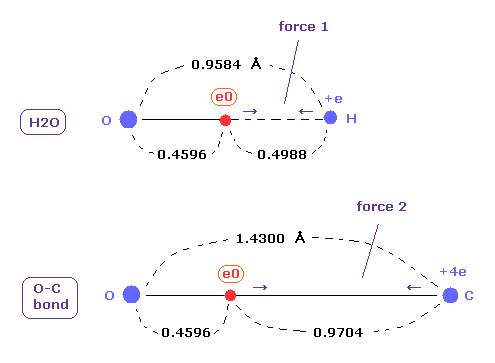
上で得たように、酸素の価電子の本当の原子半径は 1-6 の全イオン化エネルギーと 2ドブロイ波長の軌道を考慮すると 0.4596 Åである。
水の O-H 結合長は 0.9584 Åであり、平均の O-C 結合長は 1.4300 Åである。
これらの結合長から 原子半径 0.4596 を引くと、 電子と他の原子核間のクーロン力 1、2 を知ることができる。
(Fig.21) O-H と O-C 結合における クーロン力 1, 2 は ほぼ同じである。
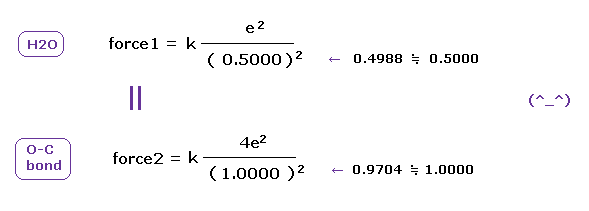
H 原子核は +eで、 C 原子核は 内殻 1s の2つの電子を引いて 約 +4e (= +6e - 2e ) である。
結果的に O-H と O-C 結合における 電子と他の原子核間のクーロン力 1 と 2 は ほぼ同じである。
なぜなら H (= 2.20 ) と C (= 2.55 ) 原子の電気陰性度は ほぼ同じだからである。
これらの結果は O-H と O-C 結合における 酸素の価電子が 共通の物理法則に従って 運動していることを示している。
また 分子中の O-H と O-C 結合において クーロンと ドブロイの関係式が重要な役割を果たしていることも示している。
(Fig.W-1) H2O における 電子分布の変化。
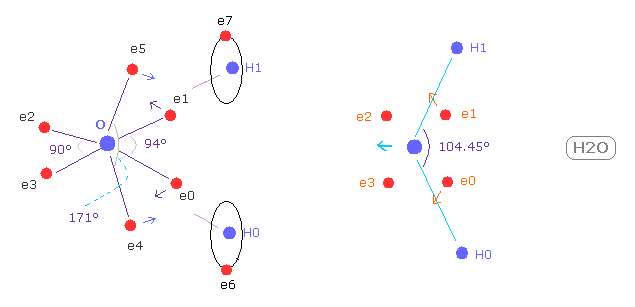
Fig.W-1 に示したように、 もし H-O-H の角度 (= 104.45° ) が 正八面体の 90°よりも 大きいと、 e0 と e1 は 水素原子核に引きつけられて 外方向へ移動する。
結果的に e0 - O - e1 角は 90°よりも広くなる。
この構造変化に続いて、 e4 - O -e5 角は もとの 180°よりも小さくなる。
結果的に 水素原子核による反発力は これらの構造変化によってキャンセルされる。( このページも参照のこと。 )
( なぜなら e4 と e5 は O 原子核を H 原子の方向へ引っ張るからである。)
(Fig.W-2) H-O-H の角度が 90°のとき、電子の構造変化がブロックされる。
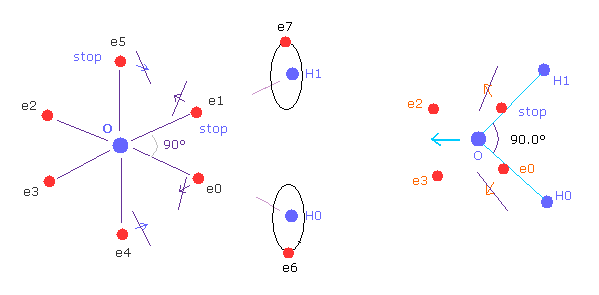
一方で、H-O-H 角が 90°のとき、 電子 e0 と e1 は 外方向へ移動できないため、 e4 と e5 も 動くことができない。
なぜなら O-e0 と O-el の線は 最初から O-H0 と O-H1 の線上にあるからである。
そのため H 原子核による反発力をキャンセルするための構造変化が起こらないことになる。
さらに H 原子核による反発力が 104.45°のときに比べて 90°のときは 角度が急になった分 強くなる。
そのため 水分子の H-O-H の角度は 強くなる反発力と 構造変化のブロックのため 90°になれないことになる。
( H-O-H の角度 104.45 のからくりは この 構造変化にあると言っていい。 )
(Fig.W-3) 四フッ化硫黄 ( SF4 ).
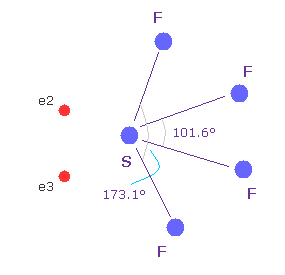
似たような構造変化は 四フッ化硫黄 (= SF4 ) で見られる。
硫黄 (= S ) は 酸素原子のように 6つの価電子を持つ。
フッ素の強い電気陰性度のために、硫黄の電子は フッ素側に引きつけられ、そのサイドの電子密度が弱くなり、これが 構造変化を引き起こす。
このメカニズムは 上記の H2O と少し異なる。しかし その構造変化は似ている。
( フッ素と水素の重要な違いは F は 7つもの価電子のため 他の原子核の価電子が多くなるにつれて それらをを反発するが、H は 引きつけられるということである。)
(Fig.22) 硫黄 ( S ) の本当の原子半径。
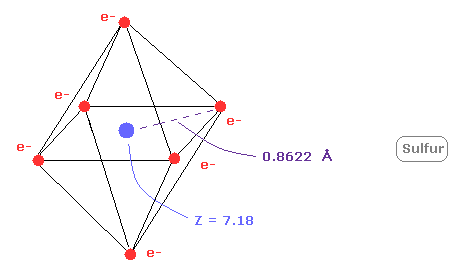
次に 硫黄 (S) の 1-6 のイオン化エネルギーの合計は 276.358 eV である。
硫黄の外殻電子は n =3 ( 3ドブロイ波長 ) の軌道のため、 この値は n=2 の炭素 (= 433.107 eV ) よりも小さい。
上記のプログラムを実行した後、 同様に "1" ( = 酸素様原子 ) を選ぶ。
そして Z = +7.18 のとき、1軌道のドブロイ波は ちょうど 3.00 になり、回転半径は 約 0.8622 Åとなる。
上で述べたように n=2 の中間の8つの電子は n=1 のよりも広く広がっている。
そのため 中心の有効電荷 (= +7.18 ) は +6 よりも大きい。
(Fig.23) C-C と C-S 結合長 ( 実験値 )。
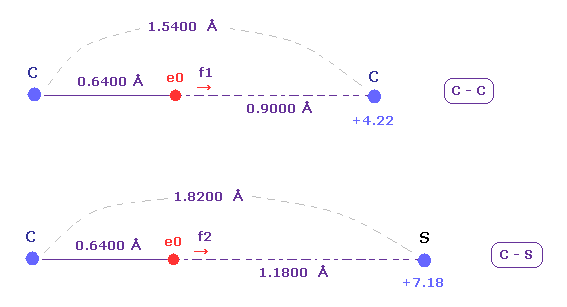
C-C と C-S 結合の実験値は それぞれ 1.5400 Å と 1.8200 Å である。
炭素 (= 2.55 ) と 硫黄 (= 2.58 ) の 電気陰性度は ほぼ 同じである。
電気陰性度は 他の原子核の電子を引き付ける力を表している。
そのため e0 に作用する力を調べる。 なぜなら この e0 は イオン化の標的電子だからである。
(Fig.24) C と S の引力は ほぼ同じである。
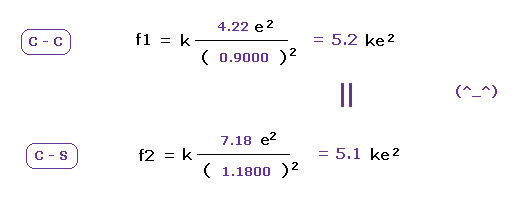
Fig.23 と Fig.24 において e0 と 他の原子核 ( C もしくは S ) の間のクーロン力 ( f1 と f2 ) を計算する。
この結果は 炭素と硫黄において 電子を引きつける力は ほぼ同じであることを示している。
これはつまり これら古典的な軌道は C と S 原子における 同じ電気陰性度と一致する ( 2.55 と 2.58 )。
(Fig.25) BF3 = 三角形。
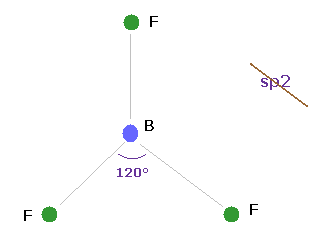
ホウ素 (= B ) は 3つの価電子を持つ。
もし 古典的なクーロン力が 正しいとしたなら、ホウ素の化合物は 三角形状になる必要がある。
実際に 3フッ化ホウ素 (= BF3 ) は 三角形上の平面であることが知られている。
そのため 元の "s" と "p" 軌道は ホウ素様原子には使えないのである。
彼らは 新たに sp2 なる概念を導入して対処しようとしているが、このことは 元の波動関数自体は 役に立たないことを意味している。
(Eq.9) ホウ素用原子の 全ポテンシャルエネルギー V。
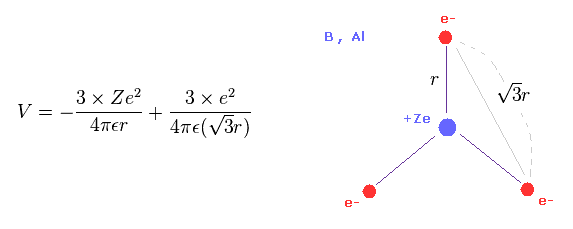
ホウ素用原子の 3つの価電子が 三角形状に分布しているとする。
電子と原子核間のクーロン相互作用を考慮すると、全ポテンシャルエネルギー V は Eq.9 のようになる。
Eq.9 では、最初の項は +Ze の原子核と 3つの電子間のポテンシャルエネルギーである。
2つめの項は 3つの価電子間の反発エネルギーである。
(Eq.10) 全運動エネルギー。
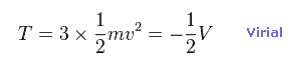
ビリアル定理 ( T = -1/2 V ) を用いると、全運動エネルギーと 各電子の速度を知ることができる。
全運動エネルギーは 3つの電子の合計である。
(Eq.11) 各電子に作用する 力 F。
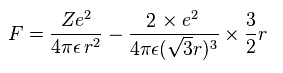
Eq.11 の 力 F は 電子に作用する力である。
Eq.11 の最初の項は +Ze 原子核による引力。
2番目の項は 他の2つの電子による反発力である。
他の原子と同様に、Eq.4 と Eq.5 を用いて 1軌道内のドブロイ波を得る。
サンプル JAVA プログラム ( 原子半径 )。
C 言語プログラム ( 原子半径 ).
ホウ素様原子 (= B、Al ) を計算するときは 最初に "2" の値を入力するように。
次に 中心電荷 Z と 1-3 の全イオン化エネルギーを入力する。
これらの入力値から、このプログラムは Eq.9 - Eq.11 と Eq.4 - Eq.5 を用いて 三角形状のホウ素の ポテンシャルエネルギーと 力を計算する。
画面上に このドブロイ波の数、電子と原子核間の距離が表示される。
| 原子名 | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| ホウ素 (B) | 8.298 | 25.155 | 37.931 | - | - | - | - |
| アルミニウム (Al) | 5.986 | 18.828 | 28.448 | - | - | - | - |
ホウ素の 1-3 のイオン化エネルギーの合計は 71.384 eV である。
Z = +3.22 のとき、 この wn は 2.00 になり、回転半径は 7996 MM. ( 1 MM = 10-14 meter. ) になる。
(Fig.26) 本当のホウ素の原子半径。
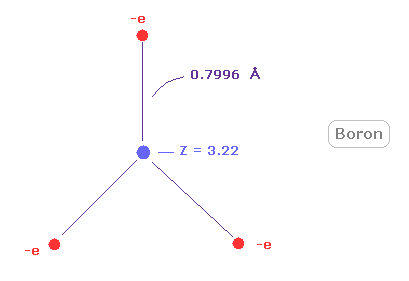
Fig.26 に示すように、ホウ素の回転半径は その小さな中心電荷 (= +3.22 ) の割には 非常に長い (= 約 0.8000 Å )。
この非常に長い原子半径は ホウ素の小さな電気陰性度 (= 2.04 ) に関係している。
(Fig.27) ボラン (= BH3 ) は 非常に不安定である。
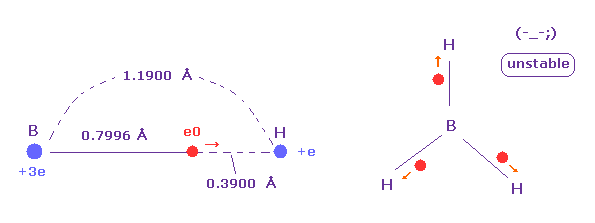
ボランは 1つのホウ素と3つの水素から成る。
このボランは 非常に不安定である。
なぜなら Fig.27 に示したように ホウ素の価電子 "e0" は その長い半径のために 水素原子核に引きつけられる傾向にあるからである。
一方で B-H 結合長は長く、ホウ素の原子核は弱い引力 ( Z = 3.0 ) しか持たないので 水素の電子と原子核は ホウ素の原子核に近づけない。
この過程では、水素の電子は ( その原子核を伴って ) e0 の電子の反発力を受けて 互いに離れる傾向になる。
(Fig.28) ジボラン (= B2H6 ) の特有な結合。
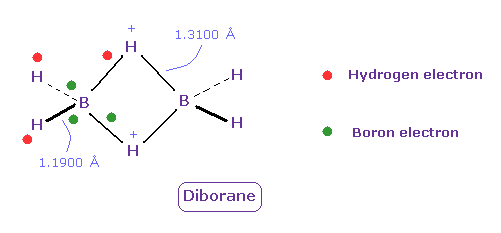
ジボラン (= B2H6 ) は無色で 室温で自然発火しやすい。
しかし ボランよりは安定である。
ホウ素は 電子不足のような 特有の結合を形成しやすい。
Fig.28 では、緑の丸が ホウ素の価電子、 赤が水素の電子である。
ホウ素の電子は 中心方向の 2つの正電荷の H 原子核に引きつけられ、外側の水素の電子も かすかに正に帯電したホウ素のほうへ引きつけられる。そのためそれらの結合は少し強くなる。
( 残念ながら、量子力学は ジボランの具体的なメカニズムについて説明できない。)
(Fig.29) アルミニウム ( Al ) の本当の原子半径。
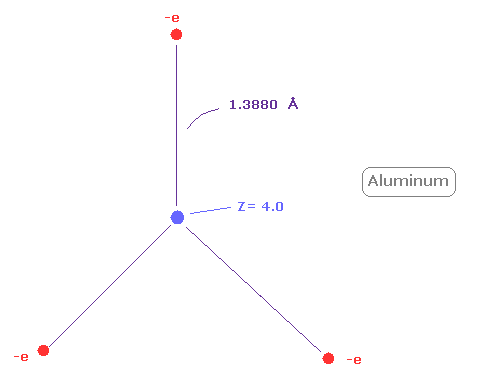
次に アルミニウム ( Al ) の 1-3 のイオン化エネルギーの合計は 53.262 eV である。
アルミニウムの外殻電子は n =3 ( 3ドブロイ波長 ) の軌道のため この値は n=2 のホウ素 (= 71.384 eV ) のより小さい。
上記のプログラムを実行後、同様に "2" ( = ホウ素様原子 ) を入力する。
Z = +4.0 のとき、1軌道内のドブロイ波は ちょうど 3.00、回転半径は 約 1.3880Åになる。
上で述べたように、n=2 の中間の8つの電子は n=1 の電子よりも もっと広く広がっている。
そのため 有効中心電荷 (= +4.0 ) は +3 よりも大きい。
(Fig.30) 弱い電気陰性度 → 水素化アルミニウム = 結晶。
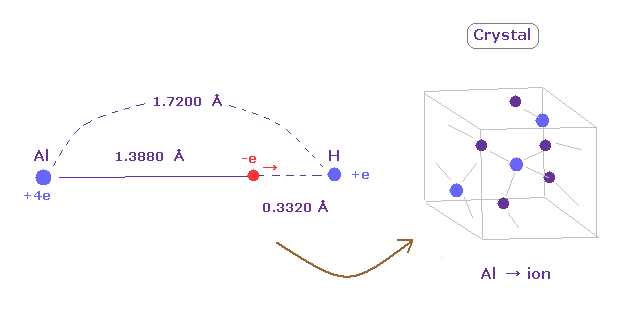
アルミニウム (Al) は 非常に長い回転半径 (= 1.3880 Å ) を持つ。
そのため その価電子は 容易にアルミニウムを離れる、つまり アルミニウムは イオン化して安定になろうとする。
例えば 水素化アルミニウムでは Al の原子核とその価電子間の距離は H 原子核間にくらべて 非常に長い。
そのため 水素化アルミニウムは結晶となり、その価電子は 自由に動きまわることによって その結晶の結合を強くしようとする。
( アルミニウムの電気陰性度は 1.61 で、 水素の 2.20 より小さい。)
Fig.28 の ジボランは 結晶の不完全バージョンと言える。
(Fig.31) 窒素における 5つの価電子の電子分布 ( 中心電荷 = +5.25e )
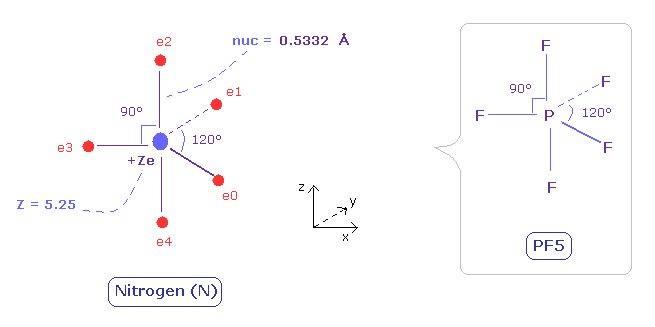
窒素原子では、炭素よりも 電子の運動を視覚化するのが難しい。
窒素は 5つの価電子を持つため、正多面体として表すことができない。
5フッ化リン ( PF5 ) は Fig.31 のような構造であることが知られている。
( リンも 窒素のように 5つの価電子を持つ。)
よって 窒素の5つの価電子が PF5 の F のように分布していると仮定する。
(Fig.31') 窒素における 5つの価電子の分布 ( 中心電荷 = +5.25e )。
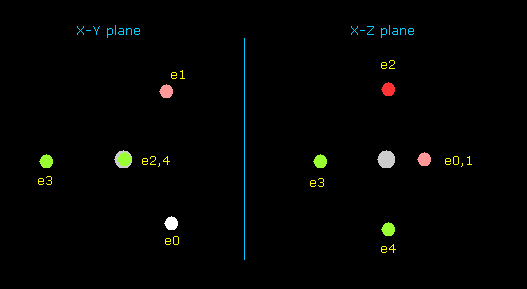
このプログラムでは、窒素原子核は 灰色の円である。
ここでは、新しい単位として ( 1 MM = 10-14 meter) を使っている。
テキストボックス内の電子の各座標 (+X (MM), +Y (MM), +Z (MM)) は、この原子核からの”相対的な”位置座標を示している。
(このテキストボックス内に値を入力して、エンターキーを押せば自由に座標の値を変更できる。)
"nuc (MM)" は各電子と核の距離を意味している。
この nuc は、所定のボックスに値を入力してエンターキーを押せば自由に変更できる。
(Fig.32) 電子と原子核に働く力。
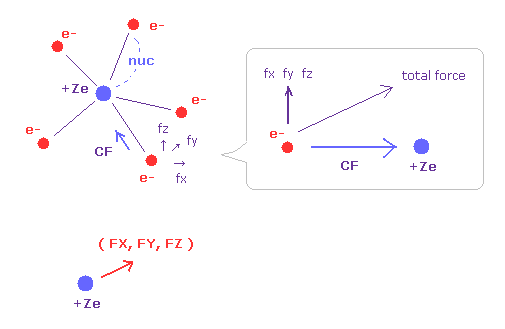
V (eV) と T (eV) は各電子の位置と運動エネルギーを意味している。
CF は各電子に作用する力の核方向の成分の量を表している。
(fx, fy, fz) は各電子に作用する力から、上の CF を除いた残りの力の各成分を表している。
つまり 窒素の5つの価電子が 原子核周囲に対称的に分布しているとき、これらの ( fx, fy, fz ) は ゼロに近くなることになる。
最後の行の (FX, FY, FZ) は核に作用する力の各成分を表している。
安定のためには これらの FX, FY, FZ もゼロに近くなる必要がある。
(Fig.33) 力 = 1000.
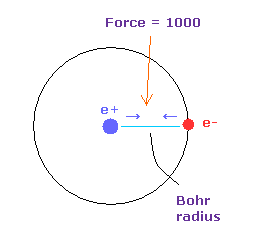
力の単位: 1000 = 互いにボーア半径離れているときの +e の原子核と -e の電子間の力である。
"tV" は 全ポテンシャルエネルギー (eV) である。
Waves (wn) は 各電子の1軌道に含まれるドブロイ波の数を表している。
| 原子名 | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| 窒素 (N) | 14.534 | 29.601 | 47.449 | 77.474 | 97.890 | - | - |
ビリアル定理によれば、”平均的な”全位置 (V) と 運動 (T) エネルギーは次の関係式を満たす。
V = 2 × E = -2 × T
窒素の5つの価電子の全エネルギーは -266.948 eV ( = 1-5th のイオン化エネルギーの和) であるため、この位置エネルギー (V) は 2 × -266.948 = -533.89 eV となる。
核の周囲に 対称的に配置されるためには、すべての価電子において、電子と核との距離がそろう必要がある。
この各電子に働く力 (F) の値を元に、Eq.4 と Eq.5 のように "仮の"半径 (r1) を定義する。
(Eq.12)
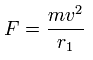
これは、”仮の”遠心力が F と等しいことを意味する。
ここで、v は各運動エネルギーを基に導かれる電子の速度である。
これらの値を基に、各電子の1軌道に含まれるド・ブロイ波の値 (wn) を次のように導く。
(Eq.13)
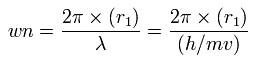
Table. 5 に示すように、 窒素の価電子の全ポテンシャルエネルギー (tV) が - 534.05 eV のとき、各電子の この wn (Waves) は ほぼ 2.0になる。
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 2666 | -4617 | 0 | 5331 | 3904 | 0 | 0 | 0 | 1.998 |
| ele 1 | 2666 | 4617 | 0 | 5331 | 3904 | 0 | 0 | 0 | 1.998 |
| ele 2 | 0 | 0 | 5332 | 5332 | 3878 | 0 | 0 | 0 | 1.992 |
| ele 3 | -5332 | 0 | 0 | 5332 | 3904 | 0 | 0 | 0 | 1.998 |
| ele 4 | 0 | 0 | -5332 | 5332 | 3878 | 0 | 0 | 0 | 1.992 |
| nuc FX | nuc FY | nuc FZ | total V (eV) | Charge Z | 半径 (MM) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | -534.05 | Z = 5.25 | nuc= 5332 |
各座標 (+X, +Y, +Z)、 nuc (MM)、 charge Z の値を自由に変更できる。
Table 5 は 窒素の5つの価電子が ほぼ
"2" ドブロイ波長の軌道を回っていることを示している。
この場合、原子核に作用する力の各成分は ( FX, FY, FZ ) = ( 0, 0, 0 ) となり、原子核が 安定であることを示している。
もちろん 各電子の (fx, fy, fz) の値は 平衡地点では ゼロに近づく必要がある。
しかし 5つの電子の価電子は 完全に対称的にはなれない。
( 実際 Fig.31 の模型では 90°と 120°が混在している。)
(Fig.34) 窒素の本当の原子半径。
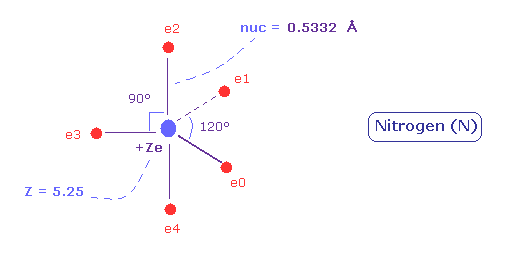
結果、窒素の価電子の本当の原子(回転)半径は 0.5332 Å になる。
また 中心電荷は +5.25 になる。
( 小さな違い 0.25 は +7e 原子核から 1s 電子が離れているためである。 )
次に n = 3 軌道に 5つの価電子を持つ リン (P) 原子について考える。
このケースでも 上記のサンプルプログラムを用いる。
| 原子名 | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| リン (P) | 10.487 | 19.770 | 30.203 | 51.444 | 65.025 | - | - |
リンの 1-5 のイオン化エネルギーは 176.929 eV である。
ビリアル定理によれば、全位置エネルギー V は 2 × 176.9 = -353.8 eV である。
窒素のプログラムを実行後、Charge Z のテキストボックスに "6.12"、nuc のテキストボックスに "9825" を入力するように。
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4912 | -8508 | 0 | 9825 | 1402 | 0 | 0 | 0 | 2.996 |
| ele 1 | 4912 | 8508 | 0 | 9825 | 1402 | 0 | 0 | 0 | 2.996 |
| ele 2 | 0 | 0 | 9825 | 9825 | 1394 | 0 | 0 | 0 | 2.988 |
| ele 3 | -9825 | 0 | 0 | 9825 | 1402 | 0 | 0 | 0 | 2.996 |
| ele 4 | 0 | 0 | -9825 | 9825 | 1394 | 0 | 0 | 0 | 2.988 |
| nuc FX | nuc FY | nuc FZ | total V (eV) | Charge Z | 半径 (MM) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | -353.58 | Z = 6.12 | nuc= 9825 |
Z = 6.12、 各電子と P 原子核の距離が 0.9825 Å ( 1 MM = 10-14 meter ) のとき、各電子軌道は ほぼ "3" ドブロイ波長になる。
(Fig.35) リン (P) の本当の原子半径。
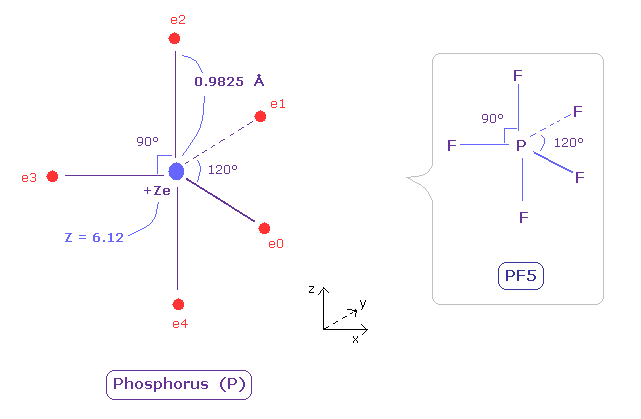
リンの半径は 窒素よりも長い。
そのため リンの電気陰性度は弱い (= 2.19 )。
広く広がった n=2 の電子のために その有効中心電荷 Z は +6.12 になり、これは +5 よりも大きい。
(Fig.36) 単一の P-P 結合長。
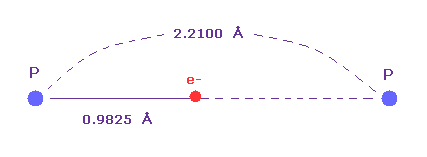
単一の P-P 結合長は 2.2100 Åであることが知られている。
ドブロイ波長に基づく原子半径 (= 0.9825 Å ) は この単一の結合長の約半分である。
つまり リン原子においても ドブロイとクーロンの関係式は 有効であることが分かる。
(Fig.N-1) 価電子間の角度は?
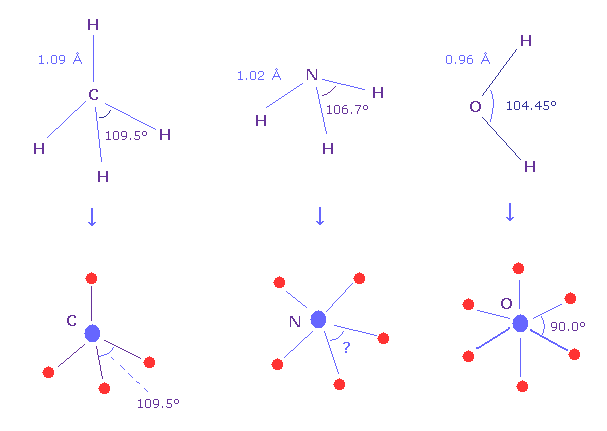
メタン分子 (= CH4 ) は ちょうど 正四面体構造であるため、H-C-H 結合角は ちょうど 109.5°である。
水の H-O-H 角は 104.45°であり、これは 正八面体の 90.0°と少し異なる。
アンモニア (= NH3 ) の H-N-H の角は 106.7°である。では 分子内での 窒素の5つの価電子間の 本当の角度は 何度なのだろうか?
(Fig.N-2) 5 と 6 価電子間の角度。
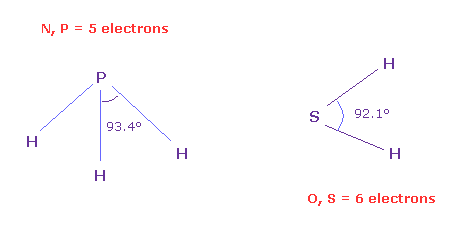
価電子間の本当の角度を知るためには、 同じ数の価電子をもつ もっと大きな原子を調べる必要がある。
なぜなら このページに示したように、H2O の 短い結合長 (= 0.96 Å ) と H 原子核の強い反発力のために、水は 正八面体構造を保てない。
一方で、SH2 の H-S 結合長は長い (= 1.34 Å ) ため、6 価電子間の より正確な角度を知ることができ (= 92.1° )、これは 90°に より近い。
また H-P 結合長 (= 1.42 Å ) は H-N 結合長 (= 1.02 Å ) よりも長い。
つまり PH3 の H-P-H 角 (= 93.4° ) は 5つの価電子間の 本当の角度に 近くなる。
実際に この値は Fig.31 の窒素模型の 90°と 120°の間である。
フッ素原子においても、電子の運動を視覚化することは 難しい。
フッ素は 7つの価電子を持つため 炭素、酸素などのように 正多面体で表せないからである。
(Fig.37) フッ素における 7 価電子の分布。
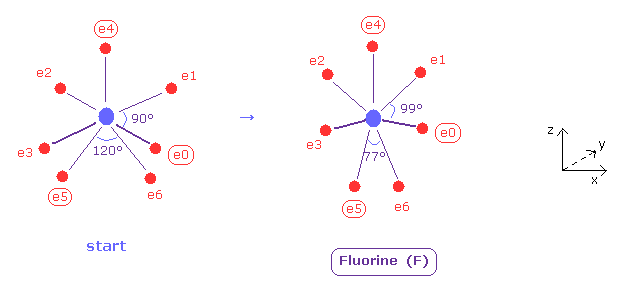
このプログラムでは Fig.37 左のフッ素の構造からスタートする。
電子 e0, e1, e2, e3 は 互いに対称的に分布、また e5, e6 も互いに対称的に分布している。
そのため e0, e4, e5 の座標のみ変化でき 他の電子座標はそれに応じて自動的に決まる。
( このスタート位置では、 e0, e1, e2, e3 は x-y 平面、e4, e5, e6 は x-z 平面上にある。)
そして それらのポテンシャルエネルギーが最も低く (= 実験値 ) なる位置を探す。
(Fig.37') フッ素の7つの価電子の分布 ( 中心電荷 = +7.3e )
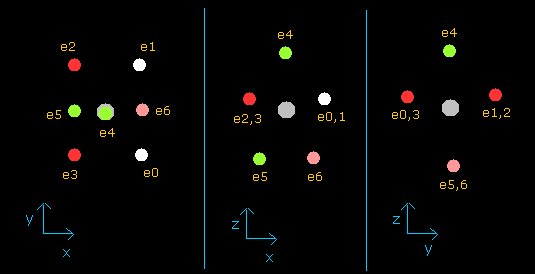
このプログラムでは フッ素原子核は 灰色である。
ここでは 新しい単位を用いている ( 1 MM = 10-14 meter)。
他の操作などは 上記の窒素と同じである。
| 原子名 | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| フッ素 (F) | 17.423 | 34.971 | 62.708 | 87.140 | 114.243 | 157.165 | 185.186 |
ビリアル定理によれば、 "平均の" 全ポテンシャル (V) と 運動 (T) エネルギーは 次の関係を満たす。
V = -2 × T = 2 × E.
フッ素の 7つの価電子の全エネルギー (E) は -658.836 eV (= 1-7 の イオン化エネルギーの合計 ) であるため、 このポテンシャルエネルギー (V) は 2 × -658.836 = -1317.67 eV となる。
Table 9 に示すように、フッ素の価電子の全ポテンシャルエネルギー (tV) が - 1317.71 eV のとき、 各電子の wn (Waves) は ほぼ 2.0 になる。
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 2537 | -3045 | 563 | 4003 | 9147 | 9 | 22 | 78 | 1.990 |
| ele 1 | 2537 | 3045 | 563 | 4003 | 9147 | 9 | -22 | 78 | 1.990 |
| ele 2 | -2537 | 3045 | 563 | 4003 | 9147 | -9 | -22 | 78 | 1.990 |
| ele 3 | -2537 | -3045 | 563 | 4003 | 9162 | 0 | 0 | 0 | 1.991 |
| ele 4 | 0 | 0 | 4003 | 4003 | 9162 | 0 | 0 | 0 | 1.991 |
| ele 5 | -2500 | 0 | -3127 | 4003 | 9119 | 162 | 0 | -130 | 1.987 |
| ele 6 | 2500 | 0 | -3127 | 4003 | 9119 | -162 | 0 | -130 | 1.987 |
| nuc FX | nuc FY | nuc FZ | total V (eV) | Charge Z | 半径 (MM) |
|---|---|---|---|---|---|
| 0 | 0 | 9 | -1317.71 | Z = 7.3 | nuc= 4003 |
座標 (+X, +Y, +Z)、 nuc (MM)、 charge Z の値は 自由に変更できる。
これらの値を変えていけば、ドブロイ波 (= Waves ) の数が ほぼ 2.0 のとき、全ポテンシャルエネルギーは 約 -1317.71 eV になる。
この結果は フッ素の7つの価電子が "2" ドブロイ波長の軌道を周回していることを示している。
このケースでは、原子核に作用する 力の各成分は ( FX, FY, FZ ) = ( 0, 0, 9 ) で ほぼゼロになり安定する。
もちろん 各電子の ( fx, fy, fz ) も 平衡状態では 小さくなる必要がある。
( 上で述べたように、これらの値は完全にゼロになれない。 )
(Fig.38) フッ素 (= F ) の本当の原子半径。
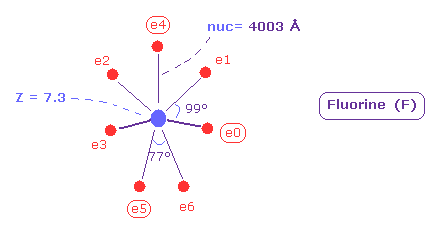
Fig.38 に示したように、 フッ素の7つの価電子の 原子(回転)半径は 0.4003 Å (= 4003 MM ) となり、この値は 非常に小さい。
また 中心電荷 Z は 7.3 になる。
(Fig.39) F の強い電気陰性度。
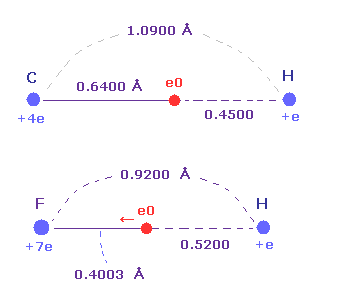
実際に F-H の結合長 (= 0.9200 Å ) は C-H 結合長 (= 1.0900 Å ) より短い。
さらに F 原子核と その価電子 e0 間の距離 (= 0.4003 Å ) は H 原子核との距離 (= 0.5200 Å ) よりも短い。その中心電荷 Z (= +7.0e ) が 水素 (= +e ) よりも 大きいにも関わらずだ。
これらの構造は フッ素の電気陰性度として現れる。
電気陰性度は F (= 3.98 )、 H (= 2.20 )、 C (= 2.55) である。
つまり この結果は クーロンとドブロイの関係式が フッ素においても有効であることを示している。
次に 塩素原子 (= Cl ) に関して考える。塩素も n = 3 のエネルギー準位に 7つの価電子を持つ。
| 原子名 | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| 塩素 (Cl) | 12.968 | 23.813 | 39.610 | 53.465 | 67.800 | 97.030 | 114.196 |
塩素の 7つの価電子の全イオン化エネルギーは 408.88 eV である。
そのため 全ポテンシャルエネルギー V は 2 × -408.88 = -817.76 eV になる。
フッ素と同じプログラムを実行後、Table 9 (= フッ素 ) の各座標と同じものを入力する。
その後、charge Z = 8.26 と nuc = 7640 を 所定の場所に入力すると 次の値を得る。
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | 4841 | -5811 | 1074 | 7640 | 2972 | 2 | 6 | 21 | 2.990 |
| ele 1 | 4841 | 5811 | 1074 | 7640 | 2972 | 2 | -6 | 21 | 2.990 |
| ele 2 | -4841 | 5811 | 1074 | 7640 | 2972 | -2 | -6 | 21 | 2.990 |
| ele 3 | -4841 | -5811 | 1074 | 7640 | 2972 | -2 | 6 | 21 | 2.990 |
| ele 4 | 0 | 0 | 7640 | 7640 | 2975 | 0 | 0 | 0 | 2.993 |
| ele 5 | -4770 | 0 | -5967 | 7640 | 2965 | 44 | 0 | -35 | 2.986 |
| ele 6 | 4770 | 0 | -5967 | 7640 | 2965 | -44 | 0 | -35 | 2.986 |
| nuc FX | nuc FY | nuc FZ | total V (eV) | Charge Z | 半径 (MM) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | -817.19 | Z = 8.26 | nuc= 7640 |
Table 11 に示すように、各電子と Cl 原子核間の距離が 0.7640 Å (= 7640 MM ) のとき、 その中心電荷は Z = 8.26 で 各軌道は ほぼ "3" ドブロイ波長になる。
( -817.19 の全ポテンシャルエネルギー V は 実験値 -817.76 eV とほぼ等しい。 )
広く広がった n = 2 の中間電子群のために 有効電荷 Z (= +8.26 ) は +7 よりも大きくなる。
(Fig.40) 塩素 (= Cl ) の本当の原子半径。
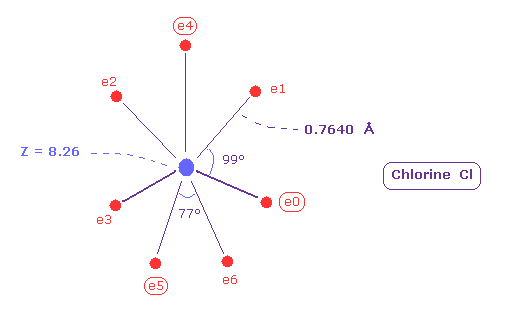
Fig.40 と Fig.38 を比較すれば、塩素の電子分布は フッ素よりも大きい。
実際に 塩素の電気陰性度 (= 3.26 ) は フッ素(= 3.98 ) のよりも小さい。
また Cl と F の広がった面積の違いは 分子結合角の違いと関係している。
(Fig.41) フルオロフォルム (= HCF3 ) と クロロフォルム (= HCCl3 )。
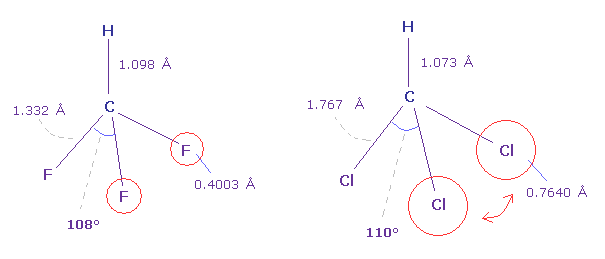
Fig.41 に示すように フルオロフォルムの F-C-F 角 (= 108.5° ) は 基本的な正四面体 (= 109.5° ) よりも小さい。
なぜなら C 原子核周囲の価電子は F のほうに引かれて F 側の電子密度が小さくなるためである。
しかし クロロフォルムの Cl-C-Cl 角は 少し大きい (= 110.4° )。 Cl が C よりも 強い電気陰性度にも関わらずだ。
なぜなら 塩素の7つの価電子は フッ素 (= 0.4003 Å ) よりも 広いエリア (= 0.7640 Å ) に分布しているからである。
これらの 反発する相互作用は クロロフォルムで わずかに強くなる。
( 塩素の価電子が広く分布しているため、塩素の正電荷の原子核が 強い反発力を生み出す。)
(Fig.42) 電気陰性度。
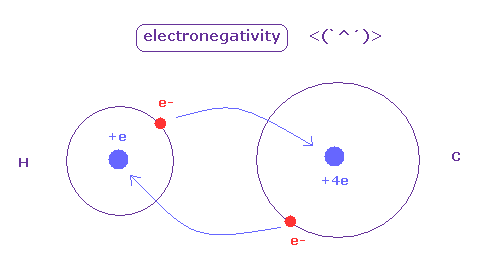
電気陰性度 ( Pauling ) は 異なったペアによって構成される 様々な分子の結合エネルギーを比較することによって得られたものである。
原子間の電気陰性度の違いが大きくなるにつれて、その結合は "イオン化" の影響がでてくるため強くなる。
電気陰性度は 各原子における 電子を引きつける力を表している。
水素と炭素原子は ほぼ同じ電気陰性度を持つ ( H = 2.20, C = 2.55 )。
C 原子核の正電荷は H のより大きいが、H 原子の電子軌道が 1ドブロイ波長なので 短い。
そのため H 原子は 自身の電子をキープしながら 他の原子核に近づくことができる。(
このことは メタンの C-H 結合長が 実験値よりも短くなれないことと関係している。)
結果、それらは ほぼ同じになる。
(Fig.43) メタンで 価電子 (= e0 ) に作用する "force 1"。

上で述べたように、1-4 の全イオン化エネルギーと "2" ドブロイ波長の軌道を考慮すると 炭素の4つの価電子の半径は 約 0.6400 × 10-10 meter である。
結果的に 価電子 e0 が 水素原子核に最も近づいたとき、それらの距離は 1.0900 (= C-H ) - 0.6400 より 0.4500 Åになる。
この地点で 炭素の価電子 e0 と H0 原子核間に クーロン力である "force 1" が作用している。
(Fig.44) エタンにおける 価電子 (= e0 ) に作用する "Force 2"。

エタンの C-C 結合長は 1.5400 Åで、価電子 e0 と C0 原子核間の距離は メタンのときのように "2" ドブロイ波長の軌道を考慮すると、 約 0.6400 Åである。
結果的に e0 と 他の炭素原子核 C1 の距離は 約 0.9000 Å (= 1.5400 - 0.6400 ) である。
また 2つの 1s 電子の効果を +6e の炭素原子核から差し引いいて 炭素 (= C1 ) の中心電荷は 約 +4e である。
"Force 2" は この e0 電子と C1 原子核間に働く力である
(Fig.45) メタンとエタンにおける クーロン力 1、 2 は ほぼ同じである。
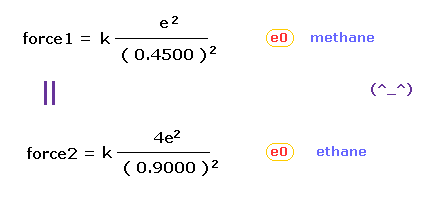
Fig.43 (= メタン ) と Fig.44 (= エタン ) から、 e0 の価電子と 他の原子核 ( H0 もしくは C1 原子核 ) 間に働く力を知ることができる。
クーロンの逆二乗の法則を使用すると、メタンの "force 1" は エタンの "force 2" にほぼ等しくなる。
この結果は H と C 原子核の ほぼ同じ電気陰性度に一致する。
(Fig.46) O-H と O-C 結合における クーロン力 1 と 2。

上で得たように、酸素の価電子の本当の原子半径は 1-6 の全イオン化エネルギーと 2ドブロイ波長の軌道を考慮すると 0.4596 Åである。
水の O-H 結合長は 0.9584 Åであり、平均の O-C 結合長は 1.4300 Åである。
これらの結合長から 原子半径 0.4596 を引くと、 電子と他の原子核間のクーロン力 1、2 を知ることができる。
(Fig.47) O-H と O-C 結合における クーロン力 1, 2 は ほぼ同じである。
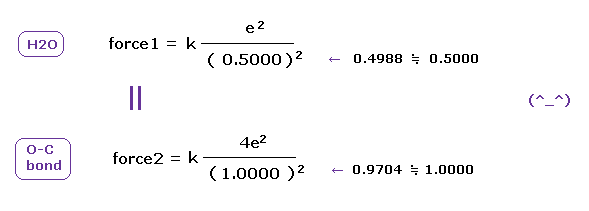
Fig.47 に示したように O-H と O-C 結合における 電子と他の原子核間のクーロン力 1 と 2 は ほぼ同じである。
そのため 酸素との結合においても H と C の電気陰性度は 本当の原子半径を用いれば ほぼ同じになる。
(Fig.48) N-H と N-C 結合における クーロン力 1, 2。
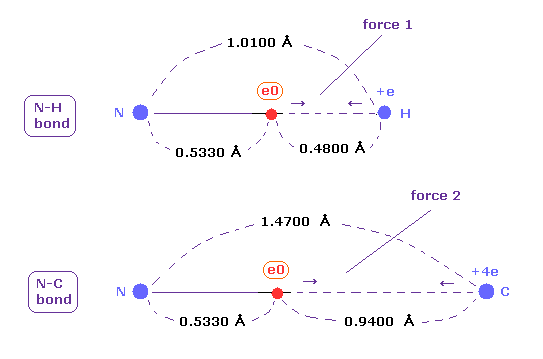
上で得たように、1-5 の 全イオン化エネルギーと 2ドブロイ波長の軌道を考慮すると、 窒素の価電子の本当の原子半径は 0.5330 Å である。
N-H 結合長は 1.0100 Åで、平均の 単一の N-C 結合長は 1.4700 Åである。
これらの結合長を 原子半径 0.5330 から差し引くと、電子と他の原子核間の力 1, 2 を知ることができる。
(Fig.49) N-H、 N-C 結合の クーロン力 1、2 は ほぼ同じである。
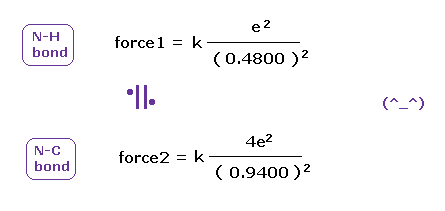
Fig.49 に示したように、窒素の結合においても 本当の原子半径を用いて H と C の 引きつける力は 同じになる。
基本的に イオン化の標的の電子は "e0" のように 他の原子に最も近づいた電子である。
水素原子は 1原子核と1電子で構成されている。
他の外殻電子 "e0" が H 原子核に最も近づいたとき、H の電子は この "e0" から離れる。
( H 原子核と 電子のこのギャップが 引力のもとになる。)
そのため 1原子核 + 1電子 がイオン化の1単位となる。
C 原子核は この単位が4ペアあると考えて H 原子核と同じ距離のもとでは その力は4倍になる。
| 原子 (= A ) | A-C 結合 ( Å ) | A-H 結合 ( Å ) | A-e0 ( Å ) | e0 - C nuc | e0 - H nuc | e0-C / e0-H |
|---|---|---|---|---|---|---|
| 炭素 (C) | C-C 1.5400 | C-H 1.0900 | 0.6400 | 0.9000 / | 0.4500 | = 2.000 |
| 酸素 (O) | O-C 1.4300 | O-H 0.9584 | 0.4596 | 0.9700 / | 0.4980 | = 1.948 |
| 窒素 (N) | N-C 1.4700 | N-H 1.0100 | 0.5330 | 0.9400 / | 0.4800 | = 1.958 |
| ホウ素 (B) | B-C 1.5500 | B-H 1.1900 | 0.8000 | 0.7500 / | 0.3900 | = 1.923 |
| フッ素 (F) | F-C 1.3500 | F-H 0.9200 | 0.4000 | 0.9500 / | 0.5200 | = 1.827 |
| ケイ素 (Si) | Si-C 1.8500 | Si-H 1.4800 | 1.1500 | 0.7000 / | 0.3300 | = 2.121 |
| リン (P) | P-C 1.8400 | P-H 1.4400 | 0.9800 | 0.8600 / | 0.4600 | = 1.870 |
| 硫黄 (S) | S-C 1.8200 | P-H 1.3400 | 0.8600 | 0.9600 / | 0.4800 | = 2.000 |
| 塩素 (Cl) | Cl-C 1.7700 | Cl-H 1.2700 | 0.7640 | 1.0060 / | 0.5060 | = 1.988 |
(Fig.50) A-H、A-C 結合の クーロン力 1, 2 は ほぼ同じ。
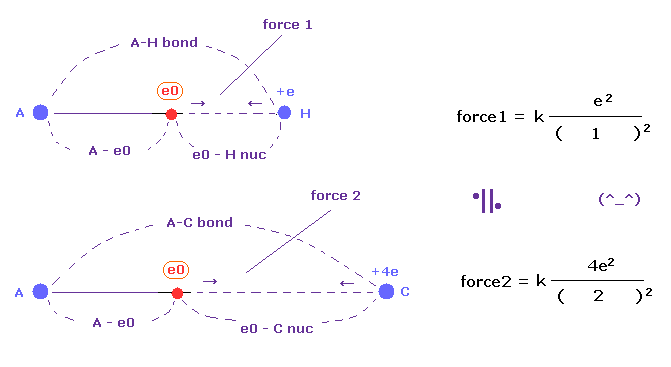
H (= 2.20 ) と C (= 2.55 ) の電気陰性度は ほぼ同じである。
これはつまり それらが他の電子を引きつける力は ほぼ同じということになる。
Fig.50 では 距離の比 e0 - C nuc / e0 - H nuc が "2.00" に近いとき、各原子核の電荷を考慮すると それらの引きつける力は等しくなる。
Table 12 に示すように、H と C の力は 様々な原子において ほぼ 同じである。
なぜなら e0 - C nuc / e0 - H nuc が ほぼ "2.00" に近いからである。
正確に言えば 炭素の電気陰性度は 水素よりも少し大きいため この比は 2.00 よりも少し小さくなる傾向にある。
(Fig.51) H、 C、 B 原子における引力。
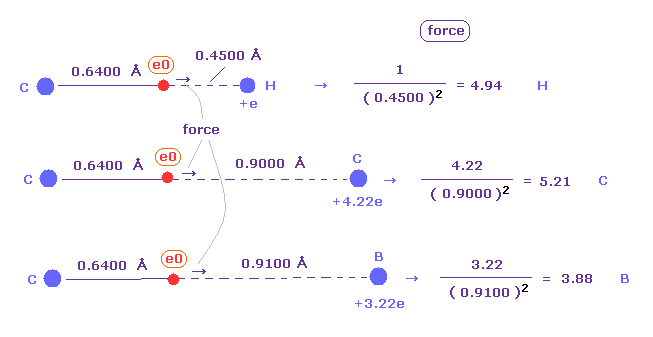
次に 各原子における 電気陰性度と 引きつける力の関係について調べる。
Fig.51 は H、C、B 原子における "e0" 電子を引きつける力を示している。
( すべてのケースで "e0" は 左側の炭素に属している。)
もちろん ドブロイ波に基づく炭素電子の回転半径 (= 0.6400 Å ) も ここでは使用している。
引力は 炭素 (= C ) で最も大きく、ホウ素 (= B ) で最も弱い。
(Fig.52) H、 C、 B 原子における引力。
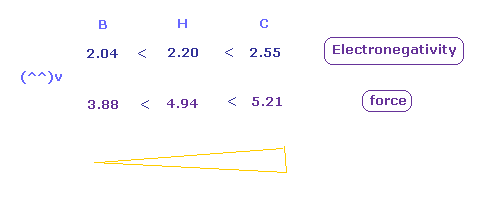
Fig.52 に示したように、電気陰性度は 力と同じように 炭素で最も強く、ホウ素で最も弱い。
この結果は 電気陰性度の視点からも クーロンとドブロイの関係式に基づく 回転半径がリアルであることを示している。
| 原子 (= A ) | 電荷 Z | C-A 結合長 ( Å ) | "e0"-A 長さ | クーロン引力 | 電気陰性度 |
|---|---|---|---|---|---|
| ケイ素 (Si) | 5.04 | C-Si 1.8500 | 1.2100 | 3.44 | 1.90 |
| ホウ素 (B) | 3.22 | C-B 1.5500 | 0.9100 | 3.88 | 2.04 |
| リン (P) | 6.12 | C-P 1.8400 | 1.2000 | 4.25 | 2.19 |
| 水素 (H) | 1.00 | C-H 1.0900 | 0.4500 | 4.94 | 2.20 |
| 炭素 (C) | 4.22 | C-C 1.5400 | 0.9000 | 5.21 | 2.55 |
| 硫黄 (S) | 7.18 | C-S 1.8200 | 1.1800 | 5.15 | 2.58 |
| 窒素 (N) | 5.25 | C-N 1.4700 | 0.8300 | 7.62 | 3.04 |
| 塩素 (Cl) | 8.26 | C-Cl 1.7700 | 1.1300 | 6.47 | 3.16 |
| 酸素 (O) | 6.27 | C-O 1.4300 | 0.7900 | 10.05 | 3.44 |
| フッ素 (F) | 7.30 | C-F 1.3500 | 0.7100 | 14.48 | 3.98 |
Table 3 に示すように、各原子において 引力と電気陰性度の間には 密接な関係があることがわかる。
一般的に 電気陰性度が大きくなるにつれて、電子を引きつける力は大きくなる。
よって ドブロイ (= 1, 2, 3 波長 ) と クーロン力が すべての原子で有効に効いていることが分かる。

2013/4/1 updated This site is link free.