トイレの台数は？

即時式完全群負荷表 erl
n＼B	0.001	0.01	0.02	0.05	0.1
1	0.001	0.01	0.02	0.05	0.11
2	0.045	0.15	0.22	0.38	0.60
3	0.193	0.46	0.60	0.90	1.27
4	0.44	0.87	1.09	1.53	2.05
5	0.76	1.36	1.66	2.22	2.88
7	1.58	2.50	2.94	3.74	4.67
10	3.09	4.46	5.08	6.22	7.51
20	9.41	12.0	13.2	15.2	17.6
50	32.5	37.9	40.3	44.5	49.6
n=台数、B=呼損率

最適な電話交換設備数、通信回線数、受付者数等を計算する場合、トラヒック理論を利用します。
それを応用して、飲食店等において必要なトイレの台数を計算してみたいと思います。
なお、トラヒック理論には即時式と待時式の２通りがあります。

1. 即時式：トイレが満杯の場合、あきらめて帰る
2. 待時式：トイレが満杯の場合、空くまで待つ

まず、台数を算出するための前提条件を考えます。

1. 入回線（人）数：最繁時の店内に入っている人数　例えば70人とする
2. 呼数c：１時間の内に何回トイレに入るか　例えば１人0.5回とすると×70人で35回となる
3. 平均保留時間h：１回当たりトイレに入っている平均時間　例えば80秒とする
4. 呼量a：呼数c×平均保留時間h＝0.5回×70人×80/3600時間＝0.78erl

即次式と即時式の２通りの計算をすると

1. 即時式：10回に１回トイレが一杯であきらめるとすると、左表の即時式アーランＢ式を用い
   呼損率B＝1/10で呼量0.78以上の値1.27からn=3で、トイレの必要台数は3台となります。
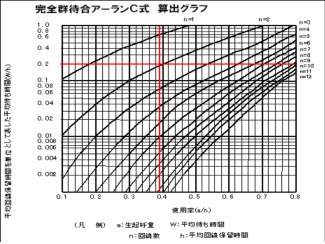
   この時の使用率は0.78/3×100で26％となります。
2. 待時式：平均待ち合わせ時間Wを16秒とすると、左図の待時式アーランＣ式を用い W/h＝16/80=0.2、 使用率a/hは n=1 の場合 0.78、n=2 の場合 0.39、n=3 の場合 0.26。
   よって、アーランＣ式のグラフからトイレの必要台数は２台となります。
   なお、平均待ち合わせ時間を10秒とした場合は３台となります。

実際には、使用状態を良く考えて、前提条件を決める必要があります。
また、アーラン算出式においても前提条件があり、多角度から現実解を求める必要があります。
br トラヒック理論の詳細は様々なサイトを参照願います。
また、計算ツールは東京工科大学菱沼研究室「コンタクトセンター用所要リソース計算サイト」がお勧めです。