1. Non-blind estimation problems

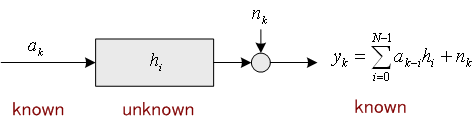
Case1: Estimate the system (impulse response) when input sequence is known.

Recursive formula of Kalman filter,

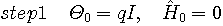
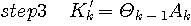
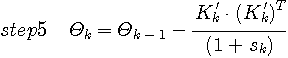
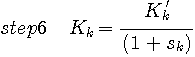
gives exact minimum of the least squares error at time L, i.e.,

Note that 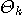tends to inverse of the correlation matrix as

,

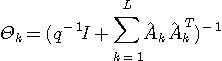and the convergence is suddenly accelerated after becomes full rank.

Case2: Estimate input sequence when impulse response is known.

Assume that symbol has discrete values and its length is finite. Then the optimum detection is given by chosing maximum of a posteriori probability. i.e.,

,

where vector denotes candidate of the symbol sequence. Under AWGN, this detection leads to MLSE (Maximum Likelihood Sequence Estimation). i.e.,

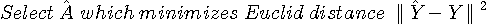
In order to extend this finite MLSE to infinite one, let us apply the following optimality principle of the dynamic programming.

For every sub-sequence 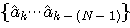contained in replica , select the minimum path (right hand side of above equation).

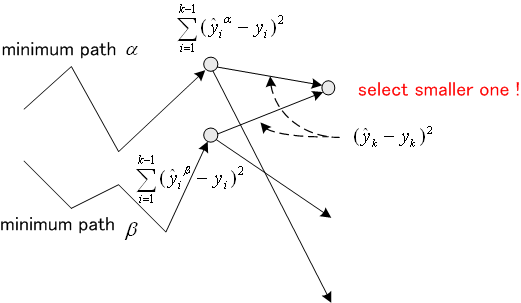
In result, each node has single coming path. Therefore, we can trace back directly without losing the way. If all traces back from nodes merge at a node, the previous path reaching to this node should be true. See the trellis graph below.

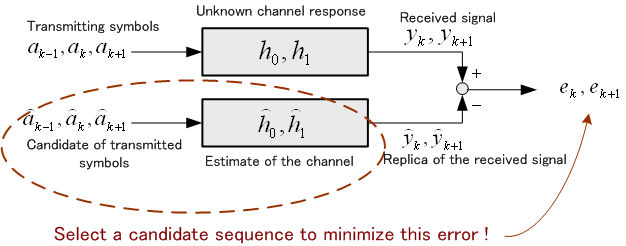
2. Two approaches to blind estimation

Suppose the simplest model of binary transmission over two-ray multi-path channel. The replica is formed by

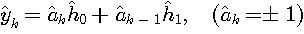
where all variables are unknown. First of all, we must define branch metric measuring distance between replica and the received signal. It is trivial that a squares error cannot be branch metric, because it has too large freedom. Therefore, branch metric may be defined by using sequence of squares error,

Note that above set of squares errors contains L+1 unknown symbols 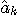and the number of candidates is . Let us define two types of branch metric for branch

.

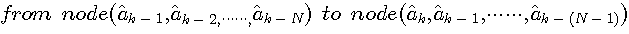(1) First definition suggested from case1 (Blind Kalman)

For each candidate 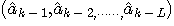, find which minimizes

,

and define the branch metric by

(2) Second definition suggested from case2 (Blind Viterbi)

For each candidate 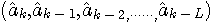, define the branch metric by the minimum of

Let us call the first and the second respectively explicit and implicit method. Both methods seem to give MLSE solution for large N. However, since we must treat rapidly faded channel, L should be chosen as small as possible.

3. Singular situations

Consider simple case of L=3. The trellis graph is drawn as below, where each node corresponds to symbol sequence; (-1,-1,-1) , (-1,-1,1) ,・・・.

(1) In the explicit method, we must find a solution 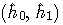of

.

However, the solution is not unique or nothing when the matrix

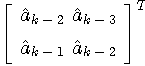
is singular. In this case, we must borrow a past solution at non-singular branch along the path reaching this node. Risk of singularity can be reduced by increasing L.

(2) The implicit method needs not to find a solution. The squares error is written as

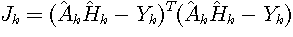
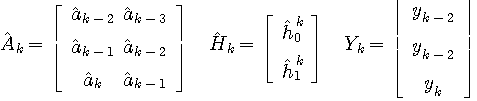
The minimum of is calculated by

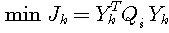
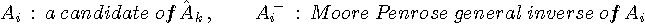
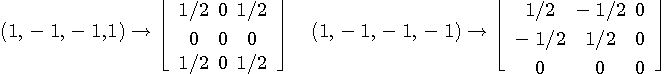
As long as 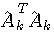is non-singular (rank=3), minimum of is realized only at true solution of .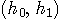

When is singular (rank<3), the least squares solution 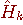cannot be unique. However, Moore-Penrose general inverse gives an unique solution satisfying with . Therefore, unbiased estimation of 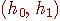is not guaranteed and is over-minimized beyond true minimum of MLSE.

4. Algebraic structure of singularity

In case of noise free, consistency of the algorithm is stated in same sentence for both cases.

Take set of L equations from long chain of equations as shown below. At each stage, find surviving candidates 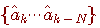which satisfy the set of equations. Such survivor, if it is false, cannot keep to survive in future. Consistency of the algorithm requires that all false survivors (paths) go to dead end and a true one remains forever.

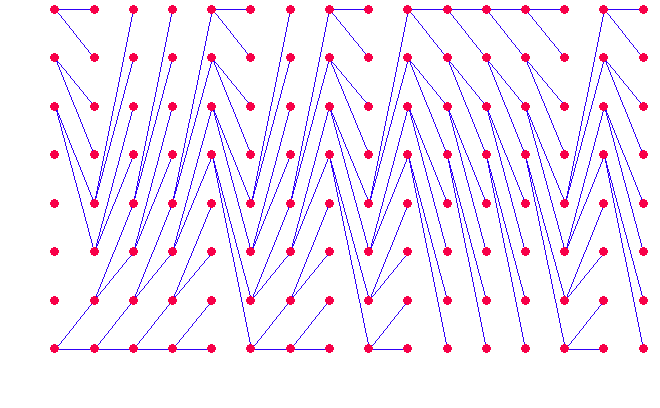
Above graph shows a case that true path remains, but we have still substantial question for the uniqueness of surviving path.

CONJECTURE

Let length of impulse response be N. If sequence keeps one-to-one correspondence to the transmitted signal , the surviving path is uniquely determined for L>N except polarity ambiguity.

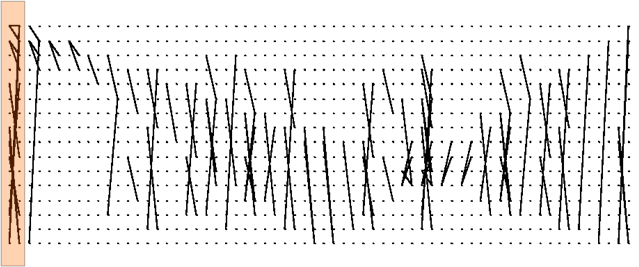
For L=4 and N=3, let us classify the branch graphs. In this case, the length of candidate becomes 6 and the number of nodes must be 32. For simple graph drawing, let us reduce the number of node in half by removing polarity ambiguity. For example, assign both (1,1,-1,1,-1) and its opposite polarity (-1,-1,1,-1,1) to a node. Thus we have a bipartite graph with 32 possible transitions (branches).The surviving branch graphs are classified into three types by property of channel response as follows.

Type 1: When the one-to-one correspondence is satisfied, the number of surviving branch is small and true path remains uniquely. Graphs below show set of surviving branch graphs and one of them is remarked by orange colored box. There are 32 graphs which correspond to 32 of the transmitted sequence patterns (note; the polarity ambiguity was removed).

It is rather significant to analyze topological regularity in these graphs.

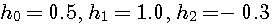
Type 2: This is a typical case that response 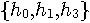has a spectrum null. If the spectrum of periodic transmitted sequence concentrates on this null point, all branches survive because the received signal vanishes. While such periodic sequence is not transmitted, all false paths go to dead end.

Type3: Another singularity is caused by time shift ambiguity such as or . In this cases, large number of branches survive and paths will frequently cross over.

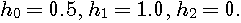
Above blind sequence detection was based on assumption that the channel can be regarded approximately as invariant in interval L. The shortest model of L=N+1 is possible to track the highest fade rate channel.
In actual noisy cases, all branches (32 in above example) have non-zero metric. By taking set of branches having small metric, we can estimate the type of current channel response. It may be an interesting work to develop the diversity or MIMO with checking the type of branch graph.

-------------------------- References ----------------------------

Sato Y:"A Blind Sequence Detection and Its Application to Digital Mobile Communication" IEEE Journal on Selected Areas in Communications, Vol.13, No.1,pp49-58, January 1995

Cited by

Miguez, J; Djuric, PM. : "Blind equalization of frequency-selective channels by sequential importance sampling".  (2004) IEEE TRANSACTIONS ON SIGNAL PROCESSING 52 (10), Pages 2738-2748, Part 1

Patwary M.N., Rapajic P., Shao X., Oppermann I.: "Adaptive Blind Sequence Detection for Time Varying Channel " (2003) Conference Record / IEEE Global Telecommunications Conference, 6, Pages 3376-3380.

Daneshgaran F., Laddomada M. : "Iterative LBG clustering for SIMO channel identification "
  (2003) Journal of Communications and Networks, 5 (2), Pages 157-166.

Daneshgaran F., Laddomada M. : "Multiscale iterative LBG clustering for SIMO channel identification "  (2002) IEEE International Conference on Communications, 1, Pages 84-88.

Daneshgaran F., Mondin M., Dovis F., Roden M.S. : "Blind estimation of output labels of SIMO channels based on a novel clustering algorithm "  (1998) IEEE Communications Letters, 2 (11), Pages 307-309.

Taylor D.P., Vitetta G.M., Hart B.D., Mammela A. : "Wireless Channel Equalisation "  
(1998) European Transactions on Telecommunications, 9 (2), Pages 117-143.

Reader D.J., Cowley W.G. : "Method for preventing delay ambiguity "  (1997) Electronics Letters, 33 (4), Pages 263-265.