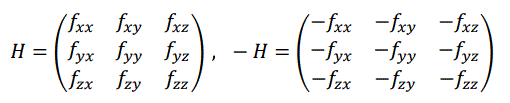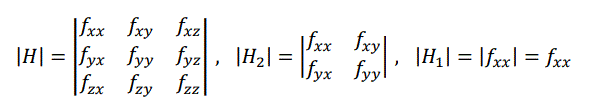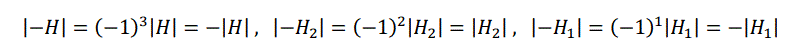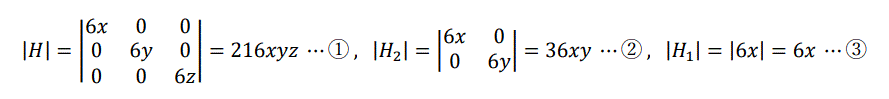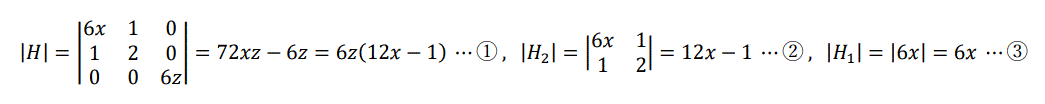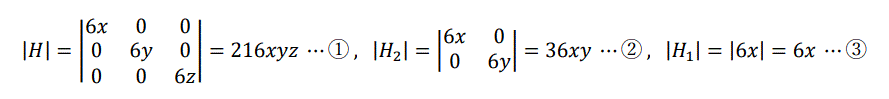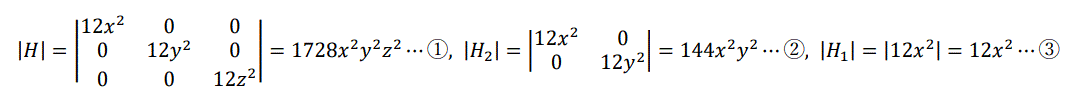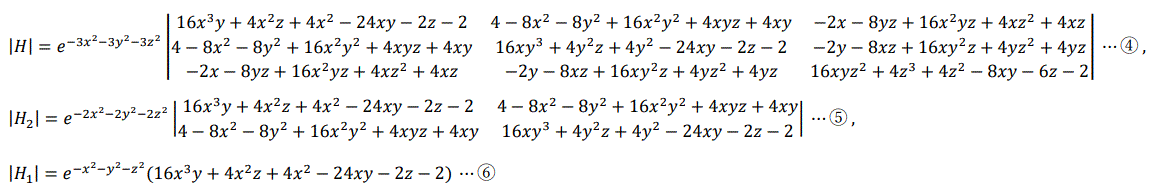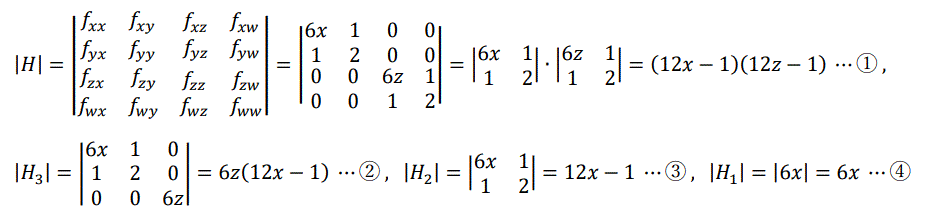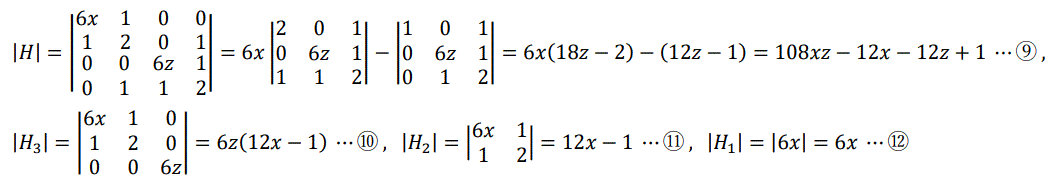３変数関数の極値判定法
３変数関数の極値判定法、すなわち、３つの変数 x, y, z を変数にもつ関数 u＝f(x, y, z) が極値（極小値、極大値）をもつかどうか、などについて調べる方法を、
以下、ご説明いたします。なお、４つ以上の変数をもつ多変数関数の極値を調べる際にも、以下に示した方法と同様の方法を用いることができます。
まず、極値をとる点は停留点でもあるので、u の停留点の座標 (x, y, z) を求めます。具体的には、f(x, y, z) の１階偏微分を求め、それを「＝０《とした式、すなわち、
∂f/∂x＝fx＝0 , ∂f/∂y＝fy＝0 , ∂f/∂z＝fz＝0 をつくり、これら３つの式を同時に満たす座標 (x, y, z) があるか否か
を調べます。もし、その様な座標が存在するなら、それは停留点の座標となっています。なお、この様にして求めた停留点の座標を（x1, y1,
z1）とします。
つぎに、f(x, y, z) の２階偏微分 fxx , fyy , fzz , fxy(＝fyx),
fxz(＝fzx), fyz(＝fzy) を求め、左下に示した３次の正方行列 Ｈ をつくります。また、右下の様に
Ｈの各成分の正負を反転させた行列 -Ｈ もつくります。なお、この正方行列 Ｈ をヘッセ行列と言います。
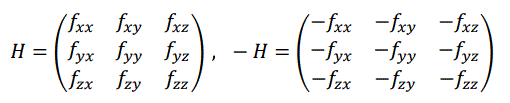
ここで、Ｈ2 をＨの左上の４つの成分をもつ２次の正方行列、Ｈ1 をＨの左上隅の成分だけをもつ１次の正方行列とし、下記の様に、
Ｈ、Ｈ2、Ｈ1 のそれぞれの行列式 |Ｈ|、|Ｈ2|、|Ｈ1| を求めます。なお、この行列式 |Ｈ| をヘッシアンと言います。
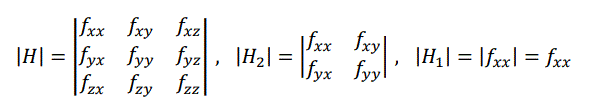
続いて、下記の様に、-Ｈ、-Ｈ2、-Ｈ1 のそれぞれの行列式 |-Ｈ|、|-Ｈ2|、|-Ｈ1| も求めます。なお、
言うまでも無いことですが、-Ｈ2 は-Ｈの左上の４つの成分をもつ２次の正方行列、-Ｈ1 は-Ｈの左上隅の成分だけをもつ１次の正方行列
です。
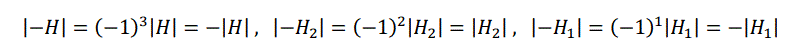
以上の準備の下で、停留点 (x1, y1, z1) における |Ｈ|、|Ｈ2|、|Ｈ1|、 |-Ｈ|、|-Ｈ2|、
|-Ｈ1| を計算すれば、以下のようにして極値をもつかどうかを判定できます。
１．|Ｈ|＞0 かつ |Ｈ2|＞0 かつ |Ｈ1|＞0 のとき、停留点 (x1, y1, z1) は極小値をとる。
２．|-Ｈ|＞0 かつ |-Ｈ2|＞0 かつ |-Ｈ1|＞0 のとき、停留点 (x1, y1, z1) は極大値をとる。
３．|Ｈ|、|Ｈ2|、|Ｈ1| はいずれも正または負の値であるが、１や２が成立しないとき、停留点 (x1, y1, z1) は鞍点となり、極値をとらない。
４．|Ｈ|、|Ｈ2|、|Ｈ1| のうち、少なくとも１つが 0 であるとき、停留点 (x1, y1, z1) が極値をとるか
否かはわからない。よって、停留点付近に
おける f(x, y, z) の変化を調べて、極値をとるか否かを判定する必要がある。
以上が３変数関数の極値判定法ですが、具体的なイメージを掴むため、いくつかの例題（例題１～例題５）をつくりましたので、以下、ご紹介いたします。
【 例題１ 】
実数 x, y, z についての３変数関数 f(x, y, z)＝x3+y3+z3-x-y-z の極値とそのときの (x, y, z) を求めなさい。
【 解答 】
まず、∂f/∂x＝3x2-1＝0 → x＝±1/√3 , ∂f/∂y＝3y2-1＝0 → y＝±1/√3 , ∂f/∂z＝3z2-1＝0 → z＝±1/√3 より、
停留点は (1/√3, 1/√3, 1/√3), (-1/√3, -1/√3, -1/√3), (1/√3, 1/√3, -1/√3), (1/√3, -1/√3, 1/√3), (1/√3, -1/√3, -1/√3),
(-1/√3, 1/√3, 1/√3), (-1/√3, 1/√3, -1/√3), (-1/√3, -1/√3, 1/√3) の計８個存在する。
また、fxx＝6x, fyy＝6y, fzz＝6z , fxy＝0, fxz＝0, fyz＝0 より、
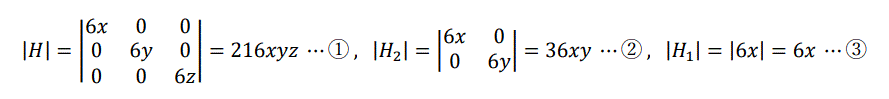
となる。
（ⅰ）(x, y, z)＝(1/√3, 1/√3, 1/√3) のとき
①～③より、|Ｈ|＝216/(3√3)＝24√3＞0、|Ｈ2|＝36/3＝12＞0、|Ｈ1|＝6/√3＝2√3＞0 となる。よって、この停留点で極小値をとり、
その値は f(1/√3, 1/√3, 1/√3)＝1/(3√3)+1/(3√3)+1/(3√3)-1/√3-1/√3-1/√3＝-2/√3＝-2√3/3 である。
（ⅱ）(x, y, z)＝(-1/√3, -1/√3, -1/√3) のとき
①～③より、|Ｈ|＝216/(-3√3)＝-24√3＜0、|Ｈ2|＝36/3＝12＞0、|Ｈ1|＝6/(-√3)＝-2√3＜0 となるから、
|-Ｈ|＝-|Ｈ|＝24√3＞0、|-Ｈ2|＝|Ｈ2|＝12＞0、|-Ｈ1|＝-|Ｈ1|＝2√3＞0 となる。
よって、この停留点で極大値をとり、その値は f(-1/√3, -1/√3, -1/√3)＝-1/(3√3)-1/(3√3)-1/(3√3)+1/√3+1/√3+1/√3＝2/√3＝2√3/3 である。
（ⅲ）(x, y, z)＝(1/√3, -1/√3, 1/√3), (1/√3, -1/√3, -1/√3), (-1/√3, 1/√3, 1/√3), (-1/√3, 1/√3, -1/√3) のとき
②より、これらの停留点では、|Ｈ2|＝36/(-3)＝-12＜0 となり、|-Ｈ2|＝|Ｈ2|＝-12＜0 となる。また、|Ｈ|≠0,
|Ｈ1|≠0 である。よって、これらの停留点は、いずれも鞍点となり、極値をとらない。
（ⅳ）(x, y, z)＝(1/√3, 1/√3, -1/√3) のとき
①、③より、|Ｈ|＝216/(-3√3)＝-24√3＜0、|Ｈ1|＝6/√3＝2√3＞0 となるから、|-Ｈ|＝-|Ｈ|＝24√3＞0、
|-Ｈ1|＝-|Ｈ1|＝-2√3＜0 となる。また、|Ｈ2|≠0 である。よって、この停留点は鞍点となり、極値をとらない。
（ⅴ）(x, y, z)＝(-1/√3, -1/√3, 1/√3) のとき
①、③より、|Ｈ|＝216/(3√3)＝24√3＞0、|Ｈ1|＝6/(-√3)＝-2√3＜0 となるから、|-Ｈ|＝-|Ｈ|＝-24√3＜0、
|-Ｈ1|＝-|Ｈ1|＝2√3＞0 となる。また、|Ｈ2|≠0 である。よって、この停留点は鞍点となり、極値をとらない。
以上より、f(x, y, z) は、(x, y, z)＝(1/√3, 1/√3, 1/√3) のときに極小値 -2√3/3 をとり、(x, y, z)＝(-1/√3, -1/√3, -1/√3) のときに
極大値 2√3/3 をとる。
（答） 極小値 -2√3/3 （ (x, y, z)＝(1/√3, 1/√3, 1/√3) のとき）、 極大値 2√3/3 （ (x, y, z)＝(-1/√3, -1/√3, -1/√3) のとき）
【 例題２ 】
実数 x, y, z についての３変数関数 f(x, y, z)＝x3+y2+z3+xy-x-y-z の極値とそのときの (x, y, z) を求めなさい。
【 解答 】
まず、∂f/∂x＝3x2+y-1＝0 , ∂f/∂y＝2y+x-1＝0 → y＝(1-x)/2 より、3x2+(1-x)/2-1＝0 →
6x2-x-1＝(3x+1)(2x-1)＝0 → x＝-1/3, 1/2 → y＝{1-(-1/3)}/2＝2/3, y＝(1-1/2)/2＝1/4 → (x, y)＝(-1/3, 2/3), (1/2, 1/4)
となり、∂f/∂z＝3z2-1＝0 → z＝±1/√3 となるから、停留点は (-1/3, 2/3, 1/√3), (-1/3, 2/3, -1/√3), (1/2, 1/4, 1/√3),
(1/2, 1/4, -1/√3) の計４個存在する。
また、fxx＝6x, fyy＝2, fzz＝6z , fxy＝1, fxz＝0, fyz＝0 より、
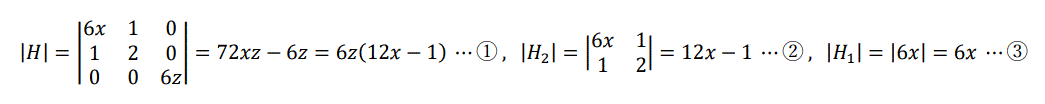
となる。
（ⅰ）(x, y, z)＝(-1/3, 2/3, 1/√3), (-1/3, 2/3, -1/√3) のとき
②より、これらの停留点では、|Ｈ2|＝12(-1/3)-1＝-4-1＝-5＜0 となり、|-Ｈ2|＝|Ｈ2|＝-5＜0 となる。また、|Ｈ|≠0,
|Ｈ1|≠0 である。よって、これらの停留点は、いずれも鞍点となり、極値をとらない。
（ⅱ）(x, y, z)＝(1/2, 1/4, 1/√3) のとき
①～③より、|Ｈ|＝6/√3{12/2-1}＝30/√3＝10√3＞0、|Ｈ2|＝12/2-1＝5＞0、|Ｈ1|＝6/2＝3＞0 となる。
よって、この停留点で極小値をとり、その値は f(1/2, 1/4, 1/√3)＝1/8+1/16+1/(3√3)+1/8-1/2-1/4-1/√3＝(2+1+2-8-4)/16+(1-3)/(3√3)＝-7/16-2√3/9
である。
（ⅲ）(x, y, z)＝(1/2, 1/4, -1/√3) のとき
①、③より、|Ｈ|＝-6/√3{12/2-1}＝-30/√3＝-10√3＜0、|Ｈ1|＝6/2＝3＞0 となるから、|-Ｈ|＝-|Ｈ|＝10√3＞0、
|-Ｈ1|＝-|Ｈ1|＝-3＜0 となる。また、|Ｈ2|≠0 である。よって、この停留点は鞍点となり、極値をとらない。
以上より、f(x, y, z) は、(x, y, z)＝(1/2, 1/4, 1/√3) のときに極小値 -7/16-2√3/9 をとる。
（答） 極小値 -7/16-2√3/9 （ (x, y, z)＝(1/2, 1/4, 1/√3) のとき）
【 例題３ 】
実数 x, y, z についての３変数関数 f(x, y, z)＝x3+y3+z3 が極値をもつかどうかを調べなさい。また、もし、極値をもつなら、
極値とそのときの (x, y, z) を求めなさい。
【 解答 】
まず、∂f/∂x＝3x2＝0 → x＝0 , ∂f/∂y＝3y2＝0 → y＝0 , ∂f/∂z＝3z2＝0 → z＝0 より、
停留点は (0, 0, 0) だけである。
また、fxx＝6x, fyy＝6y, fzz＝6z , fxy＝0, fxz＝0, fyz＝0 より、
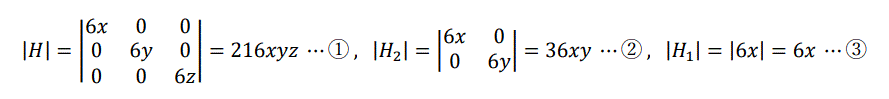
となる。
(x, y, z)＝(0, 0, 0) を①～③に代入すると、|Ｈ|＝0、|Ｈ2|＝0、|Ｈ1|＝0 となるから、f(x, y, z) が極値をとるか否かはわからない。
そこで、f(x, y, z) において y＝z＝0 と固定した f(x, 0, 0)＝x3 と言う関数について調べると、この関数は x＝0 において停留点となるが極値とはならない。
同様に、 f(0, y, 0)＝y3 や f(0, 0, z)＝z3 と言う関数も y＝0 や z＝0 において極値とはならない。
よって、f(x, y, z)＝x3+y3+z3 は、(x, y, z)＝(0, 0, 0) において停留点となるが極値とはならない。
（答） 極値をもたない
【 例題４ 】
実数 x, y, z についての３変数関数 f(x, y, z)＝x4+y4+z4 が極値をもつかどうかを調べなさい。また、もし、極値をもつなら、
極値とそのときの (x, y, z) を求めなさい。
【 解答 】
まず、∂f/∂x＝4x3＝0 → x＝0 , ∂f/∂y＝4y3＝0 → y＝0 , ∂f/∂z＝4z3＝0 → z＝0 より、
停留点は (0, 0, 0) だけである。
また、fxx＝12x2, fyy＝12y2, fzz＝12z2 , fxy＝0,
fxz＝0, fyz＝0 より、
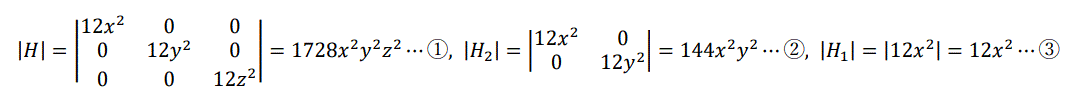
となる。
(x, y, z)＝(0, 0, 0) を①～③に代入すると、|Ｈ|＝0、|Ｈ2|＝0、|Ｈ1|＝0 となるから、f(x, y, z) が極値をとるか否かはわからない。
そこで、f(x, y, z) において y＝z＝0 と固定した f(x, 0, 0)＝x4 と言う関数について調べると、この関数は x＝0 において極小値をとる。
同様に、 f(0, y, 0)＝y4 や f(0, 0, z)＝z4 と言う関数も y＝0 や z＝0 において極小値をとる。また、
f(x, y, z)＝x4+y4+z4≧0 であり、この上等式の等号が成り立つのは (x, y, z)＝(0, 0, 0) のときだけである。
よって、f(x, y, z)＝x4+y4+z4 は、(x, y, z)＝(0, 0, 0) において極小値をとり、その値は f(0, 0, 0)＝0+0+0＝0
である。
（答） 極小値 0 （ (x, y, z)＝(0, 0, 0) のとき）
【 例題５ 】
実数 x, y, z についての３変数関数 f(x, y, z)＝(4xy+z+1)e-x2-y2-z2 が
極値をもつかどうかを調べなさい。また、もし、極値をもつなら、極値とそのときの (x, y, z) を求めなさい。
【 解答 】
まず、
∂f/∂x＝4ye-x2-y2-z2+(4xy+z+1)(-2x)e-x2-y2-z2
＝(4y-8x2y-2xz-2x)e-x2-y2-z2＝0 ---① ,
∂f/∂y＝4xe-x2-y2-z2+(4xy+z+1)(-2y)e-x2-y2-z2
＝(4x-8xy2-2yz-2y)e-x2-y2-z2＝0 ---② ,
∂f/∂z＝e-x2-y2-z2+(4xy+z+1)(-2z)e-x2-y2-z2
＝(1-8xyz-2z2-2z)e-x2-y2-z2＝0 ---③
とすると、①・yー②・x より、y2-x2＝(y-x)(y+x)＝0 → y＝x or y＝-x である。
よって、y＝x＝0 を①～③に代入して解くと (x,y,z)＝(0, 0, (-1±√3)/2) 、y＝x≠0 を①～③に代入して解くと (x,y,z)＝(±√3/4, ±√3/4, 1/4) 、
y＝-x≠0 を①～③に代入して解くと (x,y,z)＝(±√11/4, ∓√11/4, -1/4) をそれぞれ得るから、停留点は (0, 0, (-1±√3)/2)、(±√3/4, ±√3/4, 1/4)、
(±√11/4, ∓√11/4, -1/4) の６個である。
また、
fxx＝(16x3y+4x2z+4x2-24xy-2z-2)e-x2-y2-z2 ,
fyy＝(16xy3+4y2z+4y2-24xy-2z-2)e-x2-y2-z2 ,
fzz＝(16xyz2+4z3+4z2-8xy-6z-2)e-x2-y2-z2 ,
fxy＝(4-8x2-8y2+16x2y2+4xyz+4xy)e-x2-y2-z2 ,
fxz＝(-2x-8yz+16x2yz+4xz2+4xz)e-x2-y2-z2 ,
fyz＝(-2y-8xz+16xy2z+4yz2+4yz)e-x2-y2-z2
より、
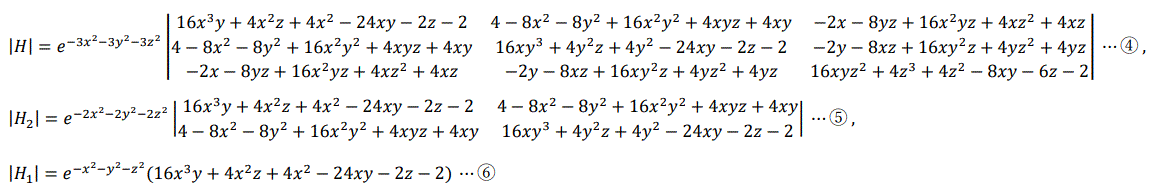
となる。
（ⅰ）(x, y, z)＝(0, 0, (-1+√3)/2) のとき
⑤より、|Ｈ2|＝(-12+2√3)e-(2-√3)＜0 となり、|-Ｈ2|＝|Ｈ2|＝(-12+2√3)e-(2-√3)＜0 となる。
また、④、⑥より、|Ｈ|＝(-12+24√3)e-(6-3√3)/2≠0, |Ｈ1|＝(-1-√3)e-(2-√3)/2≠0 である。よって、この停留点は
鞍点となり、極値をとらない。
（ⅱ）(x, y, z)＝(0, 0, (-1-√3)/2) のとき
⑤より、|Ｈ2|＝(-12-2√3)e-(2+√3)＜0 となり、|-Ｈ2|＝|Ｈ2|＝(-12-2√3)e-(2+√3)＜0 となる。
また、④、⑥より、|Ｈ|＝(-12-24√3)e-(6+3√3)/2≠0, |Ｈ1|＝(-1+√3)e-(2+√3)/2≠0 である。よって、この停留点は
鞍点となり、極値をとらない。
（ⅲ）(x, y, z)＝(√3/4, √3/4, 1/4) のとき
④～⑥より、|Ｈ|＝-96e-21/16＜0、|Ｈ2|＝24e-7/8＞0、|Ｈ1|＝-11/2e-7/16＜0 となるから、
|-Ｈ|＝-|Ｈ|＝96e-21/16＞0、|-Ｈ2|＝|Ｈ2|＝24e-7/8＞0、
|-Ｈ1|＝-|Ｈ1|＝11/2e-7/16＞0 となる。よって、この停留点で極大値をとり、その値は
f(√3/4, √3/4, 1/4)＝(4・√3/4・√3/4＋1/4＋1)e-3/16-3/16-1/16＝2e-7/16 である。
（ⅳ）(x, y, z)＝(-√3/4, -√3/4, 1/4) のとき
④～⑥より、|Ｈ|＝-96e-21/16＜0、|Ｈ2|＝24e-7/8＞0、|Ｈ1|＝-11/2e-7/16＜0 となるから、
|-Ｈ|＝-|Ｈ|＝96e-21/16＞0、|-Ｈ2|＝|Ｈ2|＝24e-7/8＞0、
|-Ｈ1|＝-|Ｈ1|＝11/2e-7/16＞0 となる。よって、この停留点で極大値をとり、その値は
f(-√3/4, -√3/4, 1/4)＝(4・√3/4・√3/4+1/4+1)e-3/16-3/16-1/16＝2e-7/16 である。
（ⅴ）(x, y, z)＝(√11/4, -√11/4, -1/4) のとき
④～⑥より、|Ｈ|＝352e-69/16＞0、|Ｈ2|＝88e-23/8＞0、|Ｈ1|＝19/2e-23/16＞0 となる。よって、
この停留点で極小値をとり、その値は f(√11/4, -√11/4, -1/4)＝(-4・√11/4・√11/4-1/4+1)e-11/16-11/16-1/16＝-2e-23/16 である。
（ⅵ）(x, y, z)＝(-√11/4, √11/4, -1/4) のとき
④～⑥より、|Ｈ|＝352e-69/16＞0、|Ｈ2|＝88e-23/8＞0、|Ｈ1|＝19/2e-23/16＞0 となる。よって、
この停留点で極小値をとり、その値は f(-√11/4, √11/4, -1/4)＝(-4・√11/4・√11/4-1/4+1)e-11/16-11/16-1/16＝-2e-23/16 である。
以上より、f(x, y, z) は、(x, y, z)＝(±√11/4, ∓√11/4, -1/4) のときに極小値 -2e-23/16 をとり、
(x, y, z)＝(±√3/4, ±√3/4, 1/4) のときに極大値 2e-7/16 をとる。
（答） 極小値 -2e-23/16 （ (x, y, z)＝(±√11/4, ∓√11/4, -1/4) のとき）、 極大値 2e-7/16
（ (x, y, z)＝(±√3/4, ±√3/4, 1/4) のとき）
最後に、４変数関数の場合について、ご説明いたします。３変数関数の場合と全く同様に、４変数関数 u＝f(x, y, z, w) では、停留点
(x1, y1, z1, w1) における |Ｈ|、|Ｈ3|、|Ｈ2|、|Ｈ1|、|-Ｈ|、
|-Ｈ3|、|-Ｈ2|、|-Ｈ1| を計算すれば、以下のようにして極値をもつかどうかを判定できます。
１．|Ｈ|＞0 かつ |Ｈ3|＞0 かつ |Ｈ2|＞0 かつ |Ｈ1|＞0 のとき、停留点
(x1, y1, z1, w1) は極小値をとる。
２．|-Ｈ|＞0 かつ |-Ｈ3|＞0 かつ |-Ｈ2|＞0 かつ |-Ｈ1|＞0 のとき、停留点
(x1, y1, z1, w1) は極大値をとる。
３．|Ｈ|、|Ｈ3|、|Ｈ2|、|Ｈ1| はいずれも正または負の値であるが、１や２が成立しないとき、停留点
(x1, y1, z1, w1) は鞍点となり、極値をとらない。
４．|Ｈ|、|Ｈ3|、|Ｈ2|、|Ｈ1| のうち、少なくとも１つが 0 であるとき、停留点
(x1, y1, z1, w1) が極値をとるか否かはわからない。よって、停留点付近に
おける f(x, y, z, w) の変化を調べて、極値をとるか否かを判定する必要がある。
４変数関数の極値判定法の具体的なイメージを掴むため、例題６、例題７をつくりましたので、以下、ご紹介いたします。
【 例題６ 】
実数 x, y, z, w についての４変数関数 f(x, y, z, w)＝x3+y2+z3+w2+xy+zw-x-y-z-w の極値とそのときの
(x, y, z, w) を求めなさい。
【 解答 】
まず、∂f/∂x＝3x2+y-1＝0 , ∂f/∂y＝2y+x-1＝0 → y＝(1-x)/2 より、3x2+(1-x)/2-1＝0 →
6x2-x-1＝(3x+1)(2x-1)＝0 → x＝-1/3, 1/2 → y＝{1-(-1/3)}/2＝2/3, y＝(1-1/2)/2＝1/4 → (x, y)＝(-1/3, 2/3), (1/2, 1/4)
となる。また、∂f/∂z＝3z2+w-1＝0 , ∂f/∂w＝2w+z-1＝0 → w＝(1-z)/2 より、3z2+(1-z)/2-1＝0 →
6z2-z-1＝(3z+1)(2z-1)＝0 → z＝-1/3, 1/2 → w＝{1-(-1/3)}/2＝2/3, w＝(1-1/2)/2＝1/4 → (z, w)＝(-1/3, 2/3), (1/2, 1/4)
となる。よって、停留点は (-1/3, 2/3, -1/3, 2/3), (-1/3, 2/3, 1/2, 1/4), (1/2, 1/4, -1/3, 2/3), (1/2, 1/4, 1/2, 1/4) の計４個存在する。
また、fxx＝6x, fyy＝2, fzz＝6z , fww＝2 , fxy＝1, fxz＝0, fxw＝0,
fyz＝0, fyw＝0, fzw＝1 より、
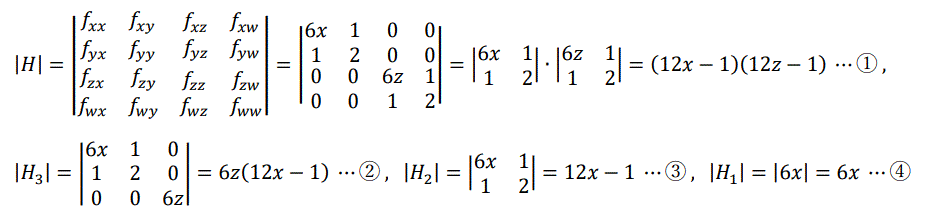
となる。
（ⅰ）(x, y, z, w)＝(-1/3, 2/3, -1/3, 2/3), (-1/3, 2/3, 1/2, 1/4) のとき
③より、これらの停留点では、|Ｈ2|＝12(-1/3)-1＝-4-1＝-5＜0 となり、|-Ｈ2|＝|Ｈ2|＝-5＜0 となる。また、|Ｈ|≠0,
|Ｈ3|≠0, |Ｈ1|≠0 である。よって、これらの停留点は、いずれも鞍点となり、極値をとらない。
（ⅱ）(x, y, z, w)＝(1/2, 1/4, -1/3, 2/3) のとき
①より、|Ｈ|＝{12/2-1}{12(-1/3)-1}＝5(-5)＝-25＜0 となり、|-Ｈ|＝|Ｈ|＝-25＜0 となる。また、|Ｈ3|≠0, |Ｈ2|≠0,
|Ｈ1|≠0 である。よって、この停留点は鞍点となり、極値をとらない。
（ⅲ）(x, y, z, w)＝(1/2, 1/4, 1/2, 1/4) のとき
①～④より、|Ｈ|＝(12/2-1)(12/2-1)＝5・5＝25＞0、|Ｈ3|＝6/2(12/2-1)＝3・5＝15＞0、|Ｈ2|＝12/2-1＝5＞0、
|Ｈ1|＝6/2＝3＞0 となる。よって、この停留点で極小値をとり、その値は
f(1/2, 1/4, 1/2, 1/4)＝1/8+1/8+1/16+1/16+1/8+1/8-1/2-1/4-1/2-1/4＝(2+2+1+1+2+2)/16-(2+1+2+1)/4＝5/8-12/8＝-7/8 である。
以上より、f(x, y, z, w) は、(x, y, z, w)＝(1/2, 1/4, 1/2, 1/4) のときに極小値 -7/8 をとる。
（答） 極小値 -7/8 （ (x, y, z)＝(1/2, 1/4, 1/2, 1/4) のとき）
【 例題７ 】
実数 x, y, z, w についての４変数関数 f(x, y, z, w)＝x3+y2+z3+w2+xy+zw+yw-x-y-z-w の極値とそのときの
(x, y, z, w) を求めなさい。
【 解答 】
まず、∂f/∂x＝3x2+y-1＝0 ---① , ∂f/∂y＝2y+x+w-1＝0 ---② , ∂f/∂z＝3z2+w-1＝0 ---③ , ∂f/∂w＝2w+z+y-1＝0 ---④
となる。よって、②＋④より 3(y+w)+x+z-2＝0 ---⑤ , ②＊④より (x+y)-(z+w)＝0 ---⑥ , ①＋③より 3(x2+z2)+y+w-2＝0 ---⑦
をそれぞれ得る。ここで、①～④の連立方程式が解をもつためには、①～④における x と z の対称性から x＝z でなければならず、x＝z と⑥より y＝w
でなければならない。よって、x＝z , y＝w を⑤に代入すると 6y+2x-2＝0 → y＝w＝(1-x)/3 ---⑧ となるから、x＝z と⑧を⑦に代入して
6x2+2(1-x)/3-2＝0 → 9x2-x-2＝0 → x＝z＝(1±√73)/18 を得る。また、この値と⑧より、y＝w＝(17∓√73)/54 を得る。
したがって、停留点は ((1+√73)/18, (17-√73)/54, (1+√73)/18, (17-√73)/54)), ((1-√73)/18, (17+√73)/54, (1-√73)/18, (17+√73)/54)) の
計２個存在する。
また、fxx＝6x, fyy＝2, fzz＝6z , fww＝2 , fxy＝1, fxz＝0, fxw＝0,
fyz＝0, fyw＝1, fzw＝1 より、
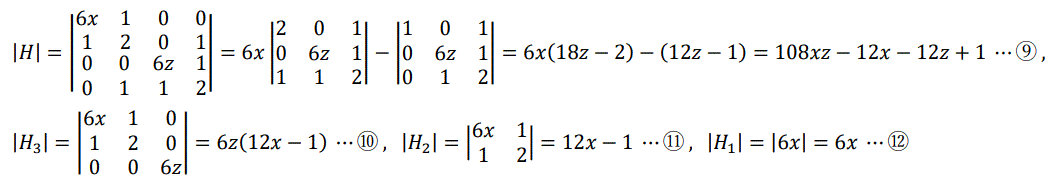
となる。
（ⅰ）(x, y, z, w)＝((1+√73)/18, (17-√73)/54, (1+√73)/18, (17-√73)/54) のとき
⑨～⑫より、|Ｈ|＝108((1+√73)/18)^2-12((1+√73)/18)2+1＝(73-2√73)/3＞0、|Ｈ3|＝6(1+√73)/18(12(1+√73)/18-1)＝(1+√73)(2√73-1)/9＞0、
|Ｈ2|＝12(1+√73)/18-1＝(2√73-1)/3＞0、|Ｈ1|＝6(1+√73)/18＝(1+√73)/3＞0 となる。よって、この停留点で極小値をとり、その値は
f((1+√73)/18, (17-√73)/54, (1+√73)/18, (17-√73)/54)＝((1+√73)/18)^3・2+((17-√73)/54)^2・2+(1+√73)/18(17-√73)/54・2+((17-√73)/54)^2
-(1+√73)/18・2-(17-√73)/54・2＝-(595+73√73)/1458 である。
（ⅱ）(x, y, z, w)＝((1-√73)/18, (17+√73)/54, (1-√73)/18, (17+√73)/54) のとき
⑪より、|Ｈ2|＝12(1-√73)/18-1＝-(1+2√73)/3＜0 となり、|-Ｈ2|＝|Ｈ2|＝-(1+2√73)/3＜0 となる。また、|Ｈ|≠0,
|Ｈ3|≠0, |Ｈ1|≠0 である。よって、この停留点は鞍点となり、極値をとらない。
以上より、f(x, y, z, w) は、(x, y, z, w)＝((1+√73)/18, (17-√73)/54, (1+√73)/18, (17-√73)/54) のときに極小値 -(595+73√73)/1458 をとる。
（答） 極小値 -(595+73√73)/1458 （ (x, y, z)＝((1+√73)/18, (17-√73)/54, (1+√73)/18, (17-√73)/54) のとき）
参考資料：
・Wikipedia 『ヘッセ行列』
・下記URL
https://science-log.com/数学/ヘッセ行列による多変数関数の極値判定/ （ 理系のための備忘録 ）
https://manabitimes.jp/math/1163 （ 多変数関数の極値判定とヘッセ行列 - 高校数学の美しい物語 - ）
