論理回路２

井澤　裕司　　

前章では、modulo 2 の除算回路の応用として、 一定の周期を有するランダムパタンを生成する回路

について紹介しました。

本章では、同じく modulo 2 の除算 の性質を用いて、

ビット誤りを検出したり修正する回路 について解説します。

ディジタル信号の伝送・記録では、 1ビットの誤りが致命的な問題を引き起こす可能性があります。

このため、フロッピーディスクやモデム、Ethernetなどのネットワークの分野では、

これらの誤りを検出するため、 巡回符号 が用いられています。

いわゆる CRC（Cyclic Redundancy Checking）符号 も、この巡回符号に属します。

送信側の符号器で、伝送するビットに 検査用のビット を追加します。

この検査ビットは、前章で説明した 原始多項式 を用いて、 ちょうど割り切れるように決定します。

伝送時に誤りが生じると、送信側と同じ原始多項式で割ったとき、 その余りは 0 になりません。

この余りの内容を解析することにより、 誤りの有無 や 誤りのあるビットの位置 を検出することができます。

本章では、このような 巡回符号による誤り検出の原理 と、 その回路構成について解説します。

2.　生成多項式

符号長が n の符号語を (a₀、a₁、a₂、‥、a_n-1) とするとき、

これを変数 x の多項式 F(x) として次のように表します。

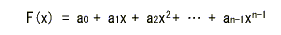
(n-1) 次 以下の多項式は全体で 2ⁿ 個存在しますが、

その中で k 次 の特別な多項式 G（x) で割り切れるものだけを符号として扱うことを考えます。

この F(x) を符号多項式、 G(x) を 生成多項式 といいます。

すなわち、符号長が n の 符号多項式 を F(x) 、 生成多項式 G(x) の次数を k とすると、

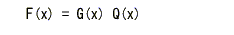
を満たす多項式 Q(x) の次数は（n - k - 1） となり、Q(x) の総数は 2^{n - k} となります。

個々の Q(x) について、それぞれ異なる符号多項式 F(x) が対応するので、

F(x) の総数も 2^{n - k} となることがわかります。

すなわち、多項式 Q(x) の各係数を （n - k）個の情報ビットに対応させることにより、

（n - k) 個の符号語 ができることになります。

x ⁿ -1 が生成多項式 G(x) で割り切れるとき、

この G(x) から生成される符号語を巡回状にシフトしたものも、 また符号語になっています。

（証明は後で示します。）

このような性質をもつ符号語を 「巡回符号」 といいます。

2.1で述べたように、（n-k）個の情報ビットを係数とする多項式 Q(x) と、

上で述べた巡回符号の生成多項式 G(x) から、 F(x) = G(x) Q（x) を計算することにより、

巡回符号を作ることができます。

しかし、このようにして生成した符号の各ビットは、 情報ビットとの対応がついていません。

そこで、次のように符号を構成することにより、 符号ビットの特定の個所に情報ビットを対応させることを考えます。

伝送するm （= n-k）個の情報ビットを係数とする多項式を P(x) で表します。

すなわち、次式が成立します。

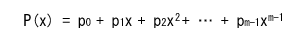
この多項式に x ^n-m を乗じ、符号多項式の高次のｍ項に対応させます。

言うまでもなく、 x ^n-m ・P(x) の低次の （n-m = k）項の係数はすべて０となります。

ここで、 x^n-m ・P(x) を 2.1で示した生成多項式 G(x) で割り、その 商を Q(x) 、余りを R(x) とします。

すなわち、

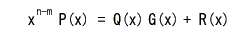
となり、余り R(x) の次数は （k-1）次以下になります。

いま、上式を変形すると次の式が得られます。

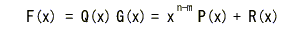
このようにすると、情報ビットは符号多項式の （n-1） 次から ｋ 次までの係数としてそのまま扱うことができます。

このような多項式 F(x) に対応する符号を伝送します。

なお、R(x) が k ビットの 検査符号 に相当します。

上で示した巡回符号に関する定理を証明しましょう。 いま、 xⁿ-1 が以下に示す F₁ (x) で割り切れるものとします。

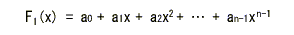
ここで F₁ (x) について符号語を循環させた関数を F₂ (x) とおくと、以下のようになります。

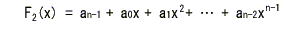
上の2式より、次の関係が成立します。

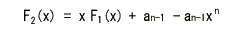
一方、 xⁿ-1 は G(x) で割り切れるので、その商を Q' (x) とおくと、

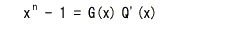
一方、 G(x) の定義より、

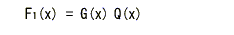
これより、次の関係式が成り立ちます。

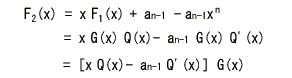
すなわち、循環変換した符号も符号語になっています。

ここでは、具体的な巡回符号の構成法について説明します。

はじめに、送信側の手順を整理しましょう。

(1)　伝送する m 個の情報ビットから多項式 x^n-m ・P(x) を求めます。

(2)　上の多項式を生成多項式 G(x) で割り、その余り R(x) を求めます。

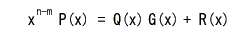
(3)　(1)の多項式 v^n-m ・P(x) と、(2)の余り R(x) の和 F(x) を求め、 対応する符号を伝送します。

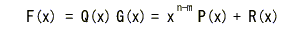
一方の受信側の手順は、以下のようになります。

(1)　送信された F(x) に伝送路で誤り E(x) が加わり、 A(x) = F(x) + E(x) を受信したものと仮定します。

(2)　伝送された A(x) を生成多項式 G(x) で割り、その余り R(x) を求めます。

(3)　もし、伝送に誤りがなければ、A(x) は G(x) で割り切れるので、余り R(x) = 0 となります。

　　逆に、誤りがあると、余り R(x) ≠ 0 となります。

それでは、簡単な例について、実際に F(x) を計算してみましょう。

例えば、n = 7，m = 4　のとき、生成多項式として G(x) = x³ + x + 1 を用います。

伝送する情報ビットが (1, 1, 1, 1) のとき、以下のように余りが求められます。

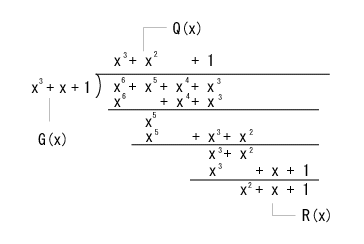
この余り R(x) は (1, 1, 1) の 3 ビットとなり、 検査ビット といいます。

これより、伝送する巡回符号は (1, 1, 1, 1, 1, 1, 1) となります。

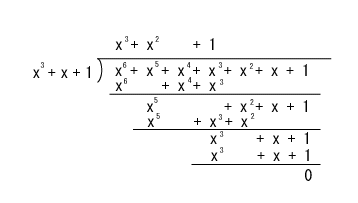
伝送路に誤りが生じなかった場合には、受信側では A(x) = F(x) を受信します。

この A(x) を生成多項式 G(x) = x³ + x + 1 で割ります。

このとき、以下のように余りは 0 となり、 誤りがなかったことがわかります。

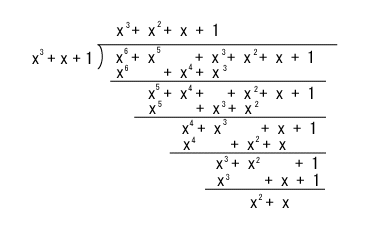
一方、伝送路で誤りが発生した場合ですが、例えば 3 ビットに誤りが生じ、

(1, 1, 0, 1, 1, 1, 1) という符号が伝送されたものとします。

この場合は、次のように余り R(x) が 0 とならないことがわかります。

次に、これを一般化した4ビットの符号 （a, b, c, d） について、巡回符号を求めてみましょう。

結果は、次のようになります。

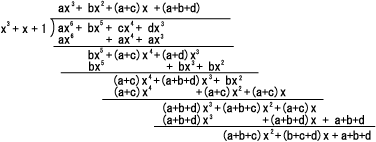
すなわち、求める F(x) は以下のようになります。

F(x) = a x⁶ + b x⁵ + c x⁴ + d x³ + (a + b + c) x² + (b + c + d) x + a + b + d

受信側では、この F(x) を生成多項式 G(x)で割ることにより、誤りの有無を調べます。

結果は以下のようになり、余りが 0 で、誤りがなかったことがわかります。

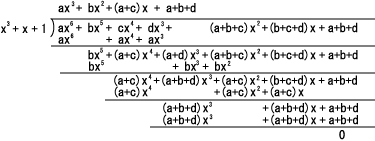
以上を、表の形に整理すると、以下のようになります。

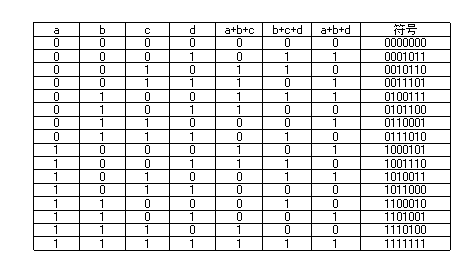
この表から、この巡回符号の最小符号間距離は 3 であることがわかります。

次に、送信された符号のうちいずれか 1ビットに誤りがあった場合について考えてみましょう。

例えば、 n = 7 ， m = 4 の例で整数 i　(0 ≦ i ≦6) とおくと、 この単一誤りは E(x) = xⁱ で表されます。

このとき受信側の符号多項式は、

F(x) + E(x) = a x⁶ + b x⁵ + c x⁴ + d x³ + (a + b + c) x² + (b + c + d) x + a + b + d + xⁱ

となります。

ここで、誤りの含まれない F(x) を G(x) で割った余りは 0 です。

したがって、 ｛F(x) + E(x) ｝ を G(x) で割った余りは、E(x) を G(x) で割った余りに等しいことがわかります。

E(x) = xⁱ は G(x) を因数にもたないので、受信側の符号多項式が G(x)で割り切れないことは明らかです。

実際に、割り算をして確かめてみましょう。

　・ x⁶ / (x³ + x + 1) = x³ + x + 1　　余り　x² + 1

　・ x⁵ / (x³ + x + 1) = x² + 1　　余り　x² + x + 1

　・ x⁴ / (x³ + x + 1) = x　　余り　x² + x

　・ x³ / (x³ + x + 1) = 1　　余り　x + 1

　・ x² / (x³ + x + 1) = 0　　余り　x²

　・ x / (x³ + x + 1) = 0　　余り　x

　・ 1 / (x³ + x + 1) = 0　　余り　1

これらの余りの値はすべて異なっており、 この値から誤ったビットの位置 [i] を求めることができます。

例えば、余りが （x² + 1） のとき上式の a を反転させ、余りが （x² + x + 1） のとき b を反転させれば、

誤りを訂正することが可能です。

次に、連続的な誤り（バーストエラー）が発生した場合について、 検討してみましょう。

次数 k の生成多項式 G(x) を用いて、 巡回符号を構成したとき、

連続する k ビット以下の誤りを検出することができます。

上の例 （n = 7、k = 3） で確認してみましょう。

連続する 3 ビットの誤りを生じる場合について、 3 次の生成多項式 G(x) = x³ + x + 1 による商と余りを求めると、

次のようになります。

　・ (x⁶ + x⁵ + x⁴) / (x³ + x + 1) = x³ + x² 　　　余り x²

　・ (x⁵ + x⁴ + x³) / (x³ + x + 1) = x² + x 　　　　余り x

　・ (x⁴ + x³ + x²) / (x³ + x + 1) = x + 1 　　　　　余り 1

　・ (x³ + x² + x) / (x³ + x + 1) = 1 　　　　　　　　余り x² + 1

　・ (x² + x + 1) / (x³ + x + 1) = 0 　　　　　　　余り x² + x + 1

　・ (x + 1 + x⁶) / (x³ + x + 1) = x³ + x + 1 　　余り x² + x

　・ (1 + x⁶ + x⁵) / (x³ + x + 1) = x³ + x² + x 　　余り x + 1

このように、上の余りは巡回構造となります。

次に、連続する 2 ビットの誤りの場合、どのようになるでしょうか。

答は、次の 7 パターンです。

　・ (x⁶ + x⁵) / (x³ + x + 1) = x³ + x² + x 　余り x

　・ (x⁵ + x⁴) / (x³ + x + 1) = x² + x + 1 　　余り 1

　・ (x⁴ + x³) / (x³ + x + 1) = x + 1 　　　　余り x² + 1

　・ (x³ + x²) / (x³ + x + 1) = 1　　　　　　　余り x² + x + 1

　・ (x² + x) / (x³ + x + 1) = 0　　　　　　　　余り x² + x

　・ (x + 1) / (x³ + x + 1) = 0 　　　　　　　　余り x + 1

　・ (1 + x⁶) / (x³ + x + 1) = (x³ + x + 1) 　余り x²

このときの余りは、3 ビットの場合における余りを、巡回状にシフトしたものとなっています。

その理由については、すでにお分かりかと思います。

（巡回符号の定義を思い起こして下さい。）

これを一般化し、生成多項式の次数を k とした場合について、

連続する k ビット以下の誤りを検出できることがわかります。

ただし、その誤りの位置を特定することはできません。

巡回符号を回路で実現する手法を紹介しましょう。

ここでは、上で説明した n = 7 、 m = 4 、 G(x) = x³ + x + 1 の回路構成を示します。

はじめに、送信側の構成です。

出力前半の 4 ビットは伝送する符号、後半の 3 ビットは余り R(x) に相当します

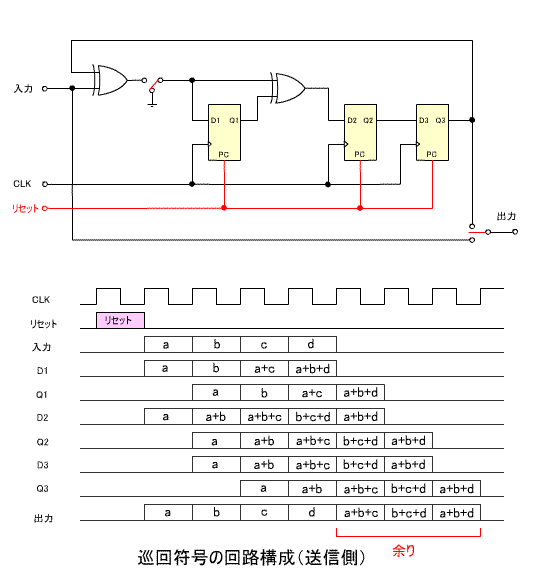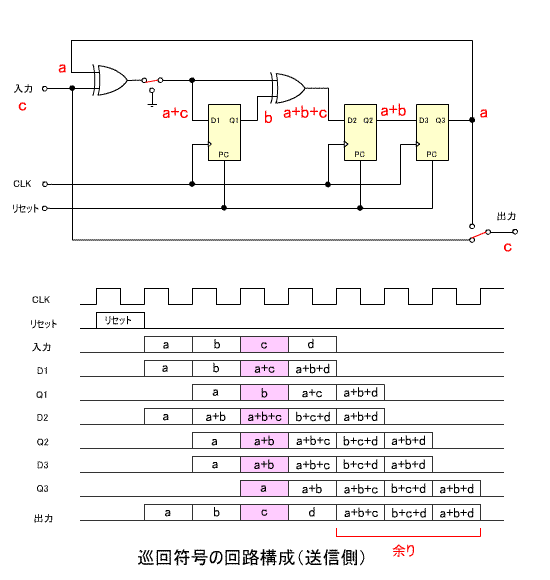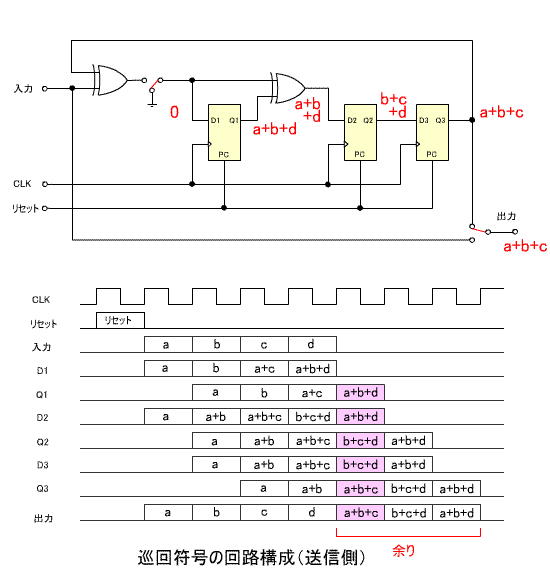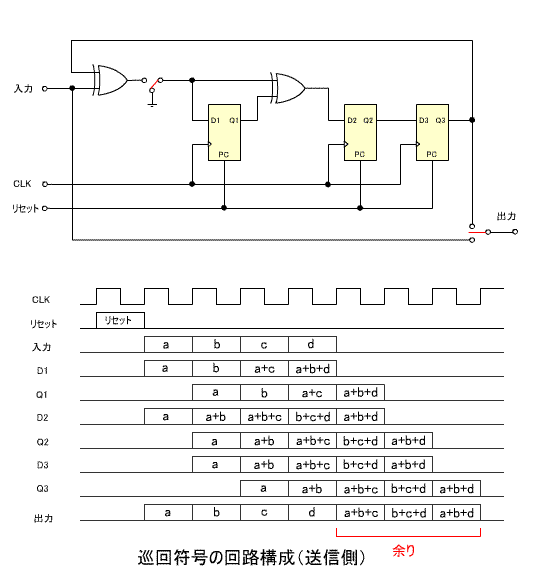
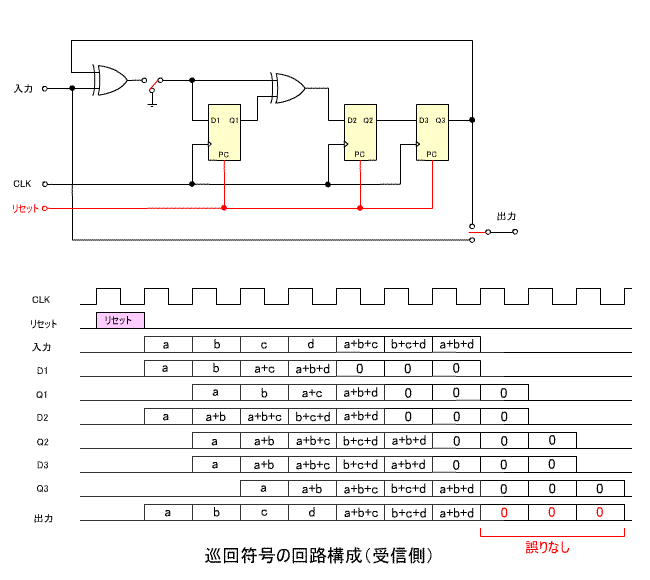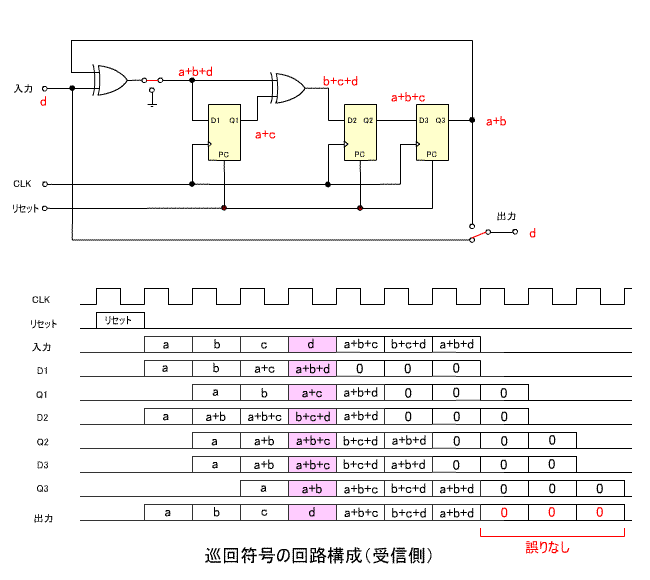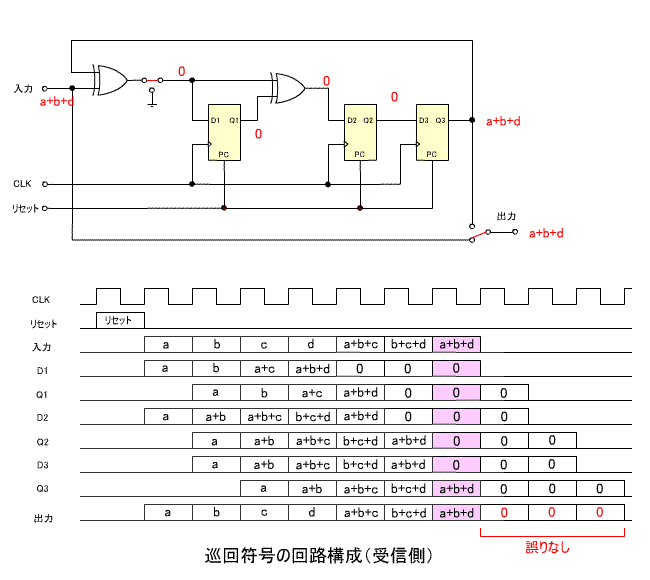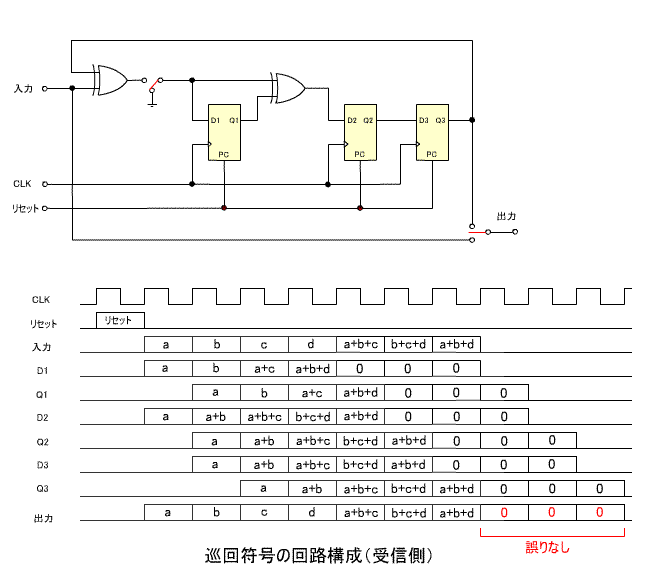
下の回路図は、受信側の構成です。

出力前半の 7 ビットは伝送された符号、後半の 3 ビットは余り R(x) に相当します。

この場合誤りがないので、余りはすべて 0 になります。

前章では巡回符号により、符号誤りが検出できることを示しました。

巡回符号では、 (xⁿ - 1) が 生成多項式 G(x) で割り切れることが条件となります。

しかし、任意の整数 n に対して、G(x) がこのような条件を満たすとは限りません。

たとえば、生成多項式 G(x) = x³ + x + 1 について、調べてみましょう。

n が 10 から 4 の場合について、 (xⁿ - 1) を G(x) で割ると次のようになります。

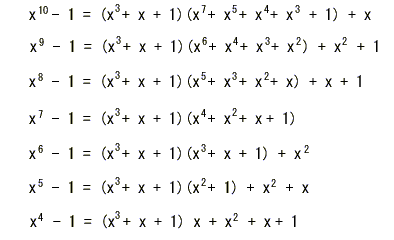
これより、 G(x) = x³ + x + 1 の場合、

10 以下の n について巡回符号となるのは、n = 7 の場合のみであり、

それ以外では巡回符号が構成できないことがわかります。

実際には、アプリケーションにより様々なビット数の誤り検出符号が必要となります。

そこで、 短縮化巡回符号 という方式が考案されました。

これを、 CRC（Cyclic Redundancy Checking）方式 と呼びます。

この方式は、 xⁿ -1 が 生成多項式 G(x) で割り切れない場合は、

G(x) で割り切れる (n - 1) 次以下の多項式を用いるというものです。

例えば、上の例で、 n = 6 、 G(x) = x³ + x + 1 の場合について検討してみましょう。

G(x) で割り切れる5次以下の多項式は以下の 8 つです。

　・　0

　・ x³ + x + 1

　・ (x³ + x + 1) x = x⁴ + x² + x

　・ (x³ + x + 1) (x + 1) = x⁴ + x³ + x² + 1

　・ (x³ + x + 1) x² = x⁵ + x³ + x²

　・ (x³ + x + 1) (x² + 1) = x⁵ + x² + x + 1

　・ (x³ + x + 1) (x² + x) = x⁵ + x⁴ + x³ + x

　・ (x³ + x + 1) (x² + x + 1) = x⁵ + x⁴ + 1

したがって、最終的な符号は次の表のようになります。

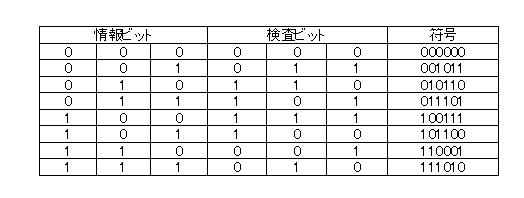
実は、この表は巡回符号の n = 7 、 G(x) = x³ + x + 1 の表の上半分（すなわちMSBが0）に対応しています。

一般には、次に示す生成多項式が用いられています。

(1)　CRC-CCITT

　　G(x) = x¹⁶ + x¹² + x⁵ + 1

(2) CRC-16

　　G(x) = x¹⁶ + x¹⁵ + x² + 1

(3) CRC-12

　　G(x) = x¹² + x¹¹ + x³ + x² + x + 1

これらの詳細については、文献等で調べて下さい。

データの誤りを検出する手法として、巡回符号を紹介し、その構成法について解説しました。

実際にモデム等で使用されているCRC符号は、ビット反転等の前処理・後処理が用いられています。

その詳細については、参考文献等で調べて下さい。

論理回路2のトップページに戻る