論理回路２

井澤　裕司　　

４章では、 非同期式 カウンタ を様々な種類のフリップフロップを用いて構成する手法について学習しました。

この非同期式カウンタの構成は単純ですが、 段数が多くなると遅延時間も大きくなるという欠点があります。

また、例えば２のべき乗以外の数を計測する場合、 非同期のクリア入力を用いるため、

ハザードが生じないような配慮が必要になります。

このような理由により、 非同期式のカウンタ が大規模なLSIで使用されることはほとんどありません。

本章では、この 非同期式 に代わって広く用いられている 同期式カウンタ の構成法について解説します。

この 同期式カウンタ の設計手法の応用範囲は極めて広く、基本的に ハザードの生じない 順序回路を構成することが可能です。

順序回路の最も重要な項目のひとつですので、 基本的な考え方をしっかり習得して下さい。

はじめに、 最も簡単な同期式カウンタの例 を示します。

クロックの立ち上りで出力 Q が反転 し、 （0→1→2→3→0→1） のようにカウントします。

エッジトリガーD-FFを2個用いている点は、 非同期式の4進カウンタと同じ ですが、

2段目FFのクロック入力が異なります。

前章で示した 非同期式カウンタの回路図 と比較し、その違いを確認して下さい。

はじめに 同期式と呼ばれる理由 について説明します。

2.1で示した 同期式カウンタのタイムチャート を拡大したものを、以下に示します。

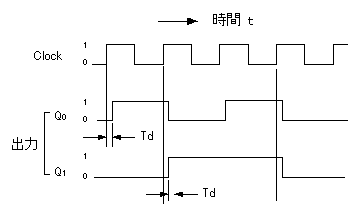
例えば、入力Clock の立上り後、 時間 td でだけ遅延して出力 Q₀が変化します。

出力 Q₁についても、Clockの立上り後 Td で変化します。

同様に、カウンタの段数を増やしても、それらの出力の遅延時間は同じで、 Clockの立上りから 1段分 の Td しかありません。

このため、 同期式カウンタ と呼ばれています。

ｎ個のD-FFを用いて、 n ビットの同期式バイナリーカウンタ を構成することが可能です。

その手法について説明します。

D-FFを用いた同期式16進カウンタ を設計してみましょう。

エッジトリガーのクロック入力のあるD-FFを4個使用して、

（0→1→2→3→4→5→6→7→8→9→10→11→12→13→14→15→0→1→2→‥）

のように計測するカウンタを構成します。

なお、クロックは定常的に入力されているものとします。

このような 4ビット16進カウンタの遷移表 を作成すると、以下のようになります。

　　　　　　　　４ビット16進カウンタの遷移表

例えば、 4個のD-FFの出力、Q₃、Q₂、Q₁、Q₀ が （ 0, 0, 1, 1） の状態にあるとします。

次のクロックの立ち上りで、 現在の状態（ 0, 0, 1, 1） に 1を加えた （0, 1, 0, 0） とする必要があります。

そのためには、 4つの入力、D₃、D₂、D₁、D₀ の各々に、 （0, 1, 0, 0） という値を与える必要があります。

これらを、現在のD-FF出力、Q₃、Q₂、 Q₁、Q₀ から作ります。

はじめに、最も下位のビット D₀ に注目して下さい。

現在の状態 Q₀ を反転したものが、 次の状態 Q₀ⁿ （= D₀）になっています。

これより、出力Q₀を反転させて、 入力D₀ に接続すればよいことがわかります。

次に2ビット目の D₁に注目して下さい。

現在の状態が10進数の（1、2、5、6、9、10、13、14） のいずれかの場合は　D₁ = 1、

それ以外（0、3、4、7、8、11、12、15）は　D₁ = 0 とします。

次に、このような条件を満たす 組合せ回路 を設計します。

なお、組合せ回路の入力は、 D-FFの出力（Q₃、Q₂、Q₁、Q₀）、

組合せ回路の出力は、D-FFの入力 D₁に接続されることに注意して下さい。

「論理回路１」 で学習した カルノー図 を用いて、 最も単純な論理関数 を求めます。

D-FF入力 D₁ のカルノー図 は、次のようになります。

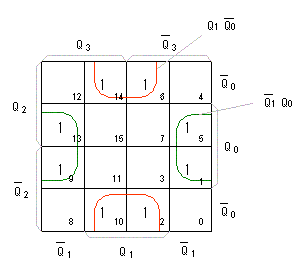
同様にして、3ビット目のD-FF入力 D₂のカルノー図 を作成します。

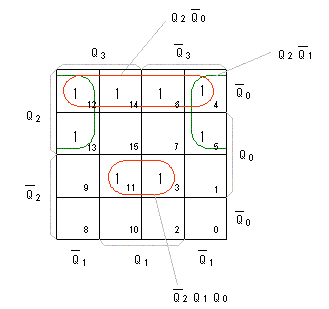
最上位4ビット目の入力 D₃ のカルノー図は、以下のようになります。

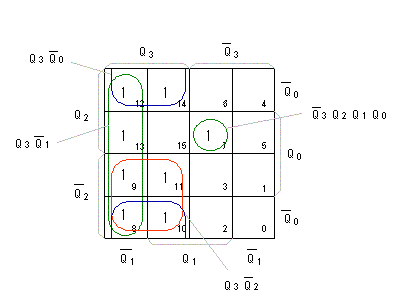
このようにして求められた論理式を以下に示します。

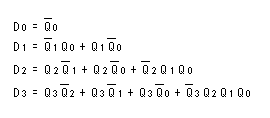
最後に、これらの論理式を、 MIL記号を用いて具体的な回路図 に変換します。

その結果を、下の図に示します。

各フリップフロップの入力が、それらの出力から合成され、 遷移表の動作を実現していることを理解して下さい。

組み合せ回路のトータルの遅延時間がクロック周期に比べて短い場合は、

原理的にハザードは生じず、安定した動作が保証されます。

このため、ハザードに対する配慮が欠かせない非同期式より、 この同期式カウンタが広く用いられています。

クロック入力付きのJK-FFを4個用いて、 同期式の4ビット16進カウンタを構成することができます。

ここでは、その実現方法について解説します。

第4章の3.2項、JK-FFを用いた1ビットカウンタの内容をもう一度復習して下さい。

このカウンタの例では、J = K = 1 とすることにより、 クロックの立ち下りで出力が反転するトグルフリップフロップとして使用しています。

もしここで、J = K = 0 とすれば、クロックが変化しても、JK-FFの出力Qは変化しません。

もう一度、D-FFを用いた4ビット16進カウンタの遷移表を示します。

なお、JK-FFの欄については、後ほど説明します。

　　　　　　　４ビット16進カウンタの遷移表 （JK-FF）

最も下位のビット Q₀ に注目して下さい。

現在の状態 Q₀ を反転したものが、 次の状態 Q₀ⁿになっています。

すなわち、J₀ = K₀ = 1とすればよいことがわかります。

これより、遷移表の右側のJ₀ （K₀ ）の欄はすべて 1となります。

次に2ビット目の Q₁に注目して下さい。

現在の状態Q₁が10進数の（1、3、5、7、9、11、13、15）のいずれかの場合、

次のクロックの立ち下りでQ₁を反転させます。

それ以外の（0、2、4、6、8、10、12、14）のときは、Q₁ は現在の状態を保持します。

これより、 現在の状態Q₁が（1、3、5、7、9、11、13、15）の場合、

　　　J_１ = K_１ = 1 、

それ以外の（0、2、4、6、8、10、12、14）のとき

　　　J_１ = K_１ = 0とすればよいことがわかります。

これらの結果を、表のJ₁ （K₁ ）の欄に記入します。

同様にして、Q₂ の欄を埋めます。

現在の状態Q₂が（3、7、11、15）のときは J₂ = K₂ = 1 、

それ以外は、J₂ = K₂ = 0 となります。

最後は、Q₃ です。

現在の状態Q₃が（7、15）のときは J₃ = K₃ = 1 、

それ以外は、J₃ = K₃ = 0 となります。

以上の結果をまとめて、遷移表の右側が完成します。

次に、論理を簡略化します。

J₀ （K₀ ）はすべて1であり、 これ以上簡略化することはできません。

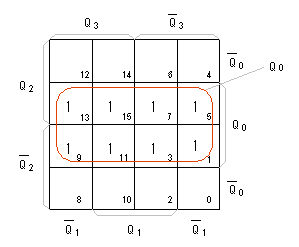
次に、 J₁ （K₁ ）について、 カルノー図を用いて簡略化します。

カルノー図は以下のようになります。これより、 J₁ = K₁ = Q₀が得られます。

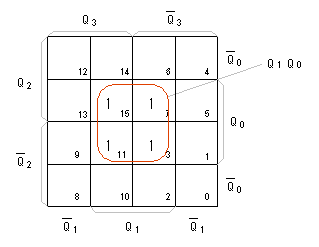
次に、 J₂ （K₂ ）について、カルノー図を作成します。

下の図から、 J₂ = K₂ = Q₁Q₀ が得られます。

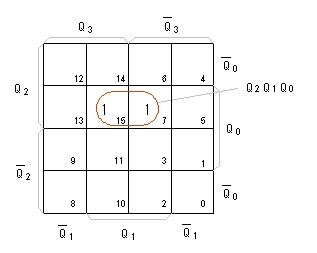
最後に、 J₃ （K₃ ）のカルノー図を作成します。

これより、 J₃ = K₃ = Q₂Q₁Q₀ が得られます。

このようにして求めた論理式を以下に示します。

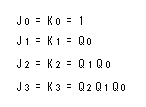
これより、以下のような回路図が得られます。

D-FFを用いた16進カウンタの回路図と比較すると、

ANDやORなどのゲートが少なくなっていることに注意して下さい。

これは、JK-FFの反転という動作条件を用いることにより、

遷移表の１の数を大幅に少なくしたことによるものです。

前節で述べたバイナリーカウンタで使用したJK-FFの代わりに、

エッジトリガーのD-FFと、排他的論理和（XOR）を用いて構成することができます。

排他的論理和（XOR）の動作については、「論理回路１」で学習しました。

XORの2つの入力を A、B、出力を Z とします。

B = 1のとき、入力A を反転させたものが出力Z となり、B = 0 のとき、Z = A となります。

エッジトリガーD-FFの出力Q をこのXORの一方の入力A に接続し、 XORの出力Z をD-FFの入力Dに繋ぎます。

XORの残る入力がHigh（B = 1）のとき、 D-FFの出力Qはクロックの立ち上りで反転する動作を繰り返します。

一方、XOR入力がLow（B = 0）のとき、 D-FFの出力Qは変化せず、その値を保持します。

このようにして、前節のJK-FFと同じような動作を、 D-FFとXORを用いて実現することが可能です。

JK-FFの入力J(K)の代わりに、XORの入力を用います。

残る組み合せ回路は、JK-FFの場合と同じです。

なお、JK-FFはクロックの立ち下り、 D-FFではクロックの立ち上りで動作することに注意して下さい。

D-FFを用いた4ビット16進カウンタの回路図を以下に示します。

前節では、２のべき乗（例えば、16）をカウントする同期式カウンタの構成法について述べました。

ここでは、２のべき乗以外、たとえば10進のカウンタを、 フリップフロップのクリア機能を用いずに構成する手法について解説します。

エッジトリガーのクロック入力のあるD-FFを4個使用して、

（0→1→2→3→4→5→6→7→8→9→0→1→2→）

となるような10進カウンタを構成します。

なお、クロックは定常的に入力されているものとします。

はじめに、遷移表を作成します。

最も下位のビット D₀ は、16進カウンタの場合と同じです。

現在の状態 Q₀ を反転したものが、 次の状態 Q₀ⁿ （= D₀）になっています。

これより、出力Q₀を反転させて、 入力D₀ に接続すればよいことがわかります。

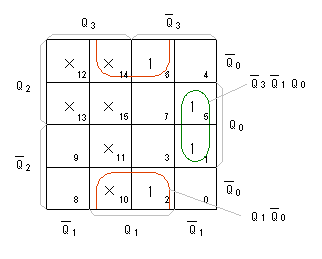
次に2ビット目の D₁に注目して下さい。

現在の状態が10進数の（1、2、5、6）のいずれかの場合は　D₁ = 1、

それ以外の（0、3、4、7、8、9）の場合は、D₁ = 0 です。

D-FF入力 D₁ のカルノー図は、次のようになります。

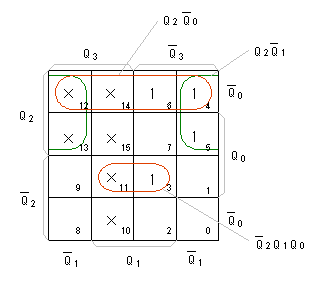
同様にして、3ビット目のD-FF入力 D₂ の カルノー図 を作成します。

最上位4ビット目の入力 D ₃ のカルノー図 は、以下のようになります。

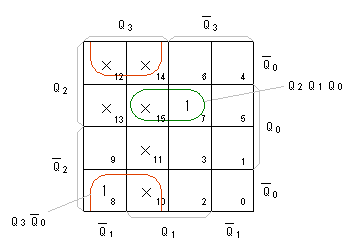
このようにして求められた論理式を以下に示します。

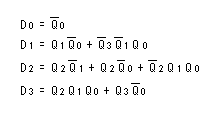
最後に、これらの論理式を、 具体的な回路図 に変換します。

その結果を、下の図に示します。

以上、D-FFを用いた10進カウンタの構成法について説明しましたが、

この設計で 腑に落ちない点 を感じた方はいますか？

もし、そのようなものを感じたとしたら、物事の本質を見抜く力が備わっている証です。

上のカウンタ回路では、（0→1→2→3→4→5→6→7→8→9→ 0→1→ ‥）

のように0から9までの数を繰り返しカウントします。

しかし、電源を投入した時点で、 フリップフロップがすべて0という値になっている保証は全くありません。

もし、4個のD-FFが（0、1、2、3、4、5、6、7、8、9）のいずれかであれば、上の遷移表に従い、

途中からでも正確に0から9までの数を繰り返しカウントします。

しかし、4個のD-FFが、（10、11、12、13、14、15）のいずれかの状態になっているとしたら、 どのようになるでしょうか？

これらの状態は、遷移表の中にはありません。

果たして、0から9までの数を正常にカウントする状態に復帰してくれるでしょうか？

上の論理式のQ₃、Q₂、Q₁、Q₀に、 10から15すなわち（1010）から（1111）の値を代入してみましょう。

その結果を、以下の表に示します。

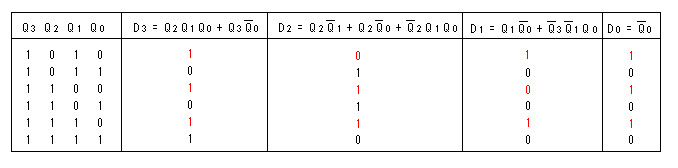
Q₃、Q₂、 Q₁、Q₀が11（1011）の場合、D₃、 D₂、D₁、D₀は（0100）すなわち 4 となり、 (11→4→5→6→‥)のようにカウントします。

したがって、正常な状態に復帰します。

同様に、Q₃、Q₂、Q₁、Q₀が13（1101）、 および15（1111）の場合、 D₃、D₂、D₁、D₀はそれぞれ4（0100）、 8（1000)となり、 問題はありません。

一方、 Q₃、Q₂、Q₁、Q₀が10（1010）の場合は、 どのようになるでしょうか？

このとき、D₃、D₂、D₁、 D₀は（1011）すなわち 11 となります。

しかし、上で述べたように11の次は4となるので、最終的には、 (10→11→4→5→‥)のようにカウントします。

同様に12（1100）の場合、一旦13 となりますが、その次は4となるので、 正常な状態に復帰します。

また、Q₃、Q₂、Q₁、Q₀が14（1110）の場合は、 次のクロックで15となりますが、そのあと8に復帰します。

すなわち、(14→15→8→9→‥)のようにカウントするので、問題はありません。

例えば先に述べた16進カウンタのように、すべての状態、 すなわち（0000）から（1111）をとりうる場合は、

このような心配は不要です。

しかし、ここで説明した10進カウンタのような場合、 電源を入れた初期状態でフリップフロップがどのような値になっていても、

必ず正常な状態に復帰することを確認しておく必要があるでしょう。

なお、一般には電源投入時に、 フリップフロップの状態を強制的にリセットする手法が用いられています。

前節では、 同期式10進カウンタの構成法 について説明しました。

nを任意の整数として、n進カウンタを設計する場合も、 これらの方法自体は全く変わりません。

例えば、0から9まで順序通りにカウントするカウンタではなく､

　　（9→8→7→6→‥）

のようにカウントダウンしたり、

　　（0→3→2→1→4→9→5→7→8→6→0→3→2→1→4→9→5→7→8→6→‥）、

のような変則的なカウンタも簡単に実現することが可能です。

ここでは、少し変わったカウントをする3bit の「変則カウンタ」を、 D-FFを用いて設計してみましょう。

例えば、

　　（0→2→4→6→7→5→3→1→0→2→4→6→7→5→3→‥）

のように偶数はカウントアップし、 その後奇数をカウントダウンするカウンタを設計します。

はじめに遷移表を作成し、例えばD-FFを用いる場合は、

次の出力Qⁿ（すなわちD）を現在の出力Qの関数で表現し、簡略化します。

そして、D-FFと、論理式に対応する組み合せ回路を用いて、回路図を作成します。

その結果を次に示します。

なお、論理式の簡略化については、各自トレースして下さい。

５　まとめ

本章では、 同期式カウンタの構成法 について解説しました。

この同期式カウンタでは、フリップフロップの非同期クリアなどの手法を用いなくても、

任意の数のカウンタを構成することができます。

ここで説明した設計手法の応用範囲はきわめて広く、 さらに高度な順序回路に応用することが可能です。

次章では、たとえばシフトレジスタなど、 カウンタ以外の順序回路の構成法について説明します。

論理回路2のトップページに戻る