論理回路２

第４章 順序回路の基礎（その３）
　　−カウンタ回路（非同期式）−

　　　　　　　　　　　　　　　　　井澤　裕司　　

代表的な 順序回路 に カウンタ があります。

カウンタとは、入力となるクロックや信号の数を計測する回路であり、 コンピュータをはじめ、様々なICやLSIに数多く用いられています。

例えば、ディジタル時計では、1秒に1回のパルス信号を60回計測して、1分を計測します。

同様に、1分を60回、1時間を24回、1日を30回（あるいは29、31回） 計測するカウンタ群が内蔵されています。

このカウンタには、クロックに同期して動作する

同期式カウンタ と、そうではない 非同期式カウンタ があります。

本章では、比較的簡単に実現できる 非同期式カウンタ の構成法について解説します。

第3章で説明した 1ビットの2進カウンタを ｎ 個 用い、これらを 従属接続 すれば ｎビットのバイナリーカウンタを 構成することができます。

例えば、最も単純な エッジトリガーの T-FF を３個用いて、

　　　1段目の出力を2段目の入力

　　　2段目の出力を3段目の入力

のように接続すれば、3ビットのカウンタが構成されます。

このカウンタは、 （0→1→2→3→4→5→6→7→0→1） というように、１クロックごとに カウントアップ します。

出力は3ビットの 2進数(000〜111) です。

ここで、カウンタの出力は、 T-FFの反転出力 であることに注意して下さい。

なお、各フリップフロップのQを直接出力すれば、（7→6→5）というように、 カウントダウン するカウンタとなります。

その回路図とタイムチャートは、以下のようになります。

原理的には、このT-FFを n 個従属接続すれば、 n ビットの2進カウンタを構成することが可能です。

2.2　非同期式カウンタの遅延について

はじめに 非同期式と呼ばれる理由 について説明します。

2.1で示した 非同期式カウンタのタイムチャート を拡大したものを、以下に示します。

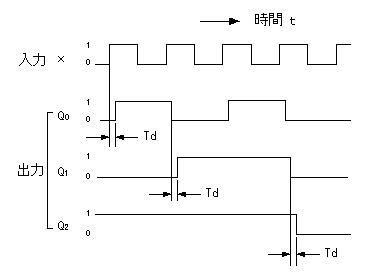
例えば、入力 x の立上り後、時間 td でだけ遅延して出力 Q0 が変化します。

また、出力 Q1 は出力 Q0 の立下り後 Td で変化し、

さらに、出力 Q2 は Q1 の立下り後td で変化します。

したがって、入力 x の立上りから計測すると、出力の Q2 には 3段分の遅延 が含まれることになります。

このように、非同期式で ｎビットのカウンタ を構成する場合、

遅延時間も ｎ倍 されることを考慮しなければなりません。

３　非同期式バイナリーカウンタ

以下にJK-FFを2個用いた 2ビット4進カウンタ を示します。

このJK-FFは、 クロック入力のあるDC型 です。

なお入力J＝1、ｋ＝1となっているため、 クロックの立ち下りで出力 Q が反転 し、

（0→1→2→3→0→1）のようにカウントします。

D-FFを用いた2ビット4進カウンタは、下の図のようになります。

この D-FFはエッジトリガータイプ であり、D-FFの反転出力が入力Dに接続しているため、

クロックの立ち上りで出力Qが反転 します。

４　非同期クリアによるｎ進カウンタ

前章では、様々なフリップフロップを用いた バイナリーカウンタの構成法を示しました。

これにより、(0→3)や(0→7)のように、 （２のべき乗−1）までの数を繰り返し計測することができます。

しかし、10（9）や24（23）のように、２のべき乗ではない数値をカウントするためには、

どのようにすればよいでしょうか？

このような場合、クロック入力の状態にかかわらず、 無条件に出力Qを 0 にリセットする

クリア入力（非同期クリア入力） のあるフリップフロップを用います。

これから、具体的な例を用いてその方法を説明しましょう。

JK-FFを用いた５進カウンタ を設計してみましょう。

JK-FFの中に、クロック入力の状態にかかわらず無条件に

出力 Q を 0 にクリアする入力 C が備わっている種類があります。

クロック入力の状態に依存しないので、 非同期クリア と呼ぶことがあります。

負論理（0 のときクリア）を明示的に表すため、図の入力部に○が付いています。

このような非同期クリア入力をもつJK-FFを、図のように3個従属接続します。

3個のFF出力が2進数の（101）になった直後、 3入力NAND回路を用いて、クリア入力 C を 0 にします。

3個のフリップフロップの出力が 0 にクリアされると、 NAND回路のクリア信号 C は 1に戻るため、

フリップフロップのクリアは解除されますが、 FF出力はすべて 0 の状態を保ちます。

そして、再び（0→1→2→）のように、カウントを開始します。

この非同期式カウンタは

　　　（0→1→2→3→4→5→0→1）

のように動作しますが、 5の状態はきわめて短く、 すぐ 0 となるので、実質的には、

　　　（0→1→2→3→4→0→1）

の5進カウンタとみなすことができます。

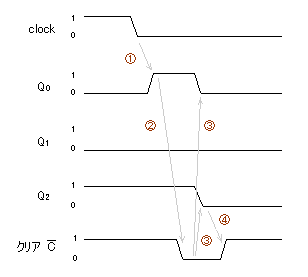
下の図を用いて、FF出力が5→0となる瞬間について詳しく調べてみましょう。

　　�@　クロックの立ち下りにより、Q₀ が 0 から 1 に変化する。

　　�A　Q₀が 1 になったため、NAND回路によりクリア信号（負論理）が 0 となる。

　　�B　Q₀ と Q₂ がクリアされ 0 となる。（Q₁は 0 で変わらず）

　　�C　Q₀ と Q₂が変化したため、クリアが解除される（1となる）。

この回路では、3個のFFの出力が（101）以外の値になるまで、 クリア信号を出し続けます。

したがって、FFの特性に大きなバラツキがない限り、安定に動作します。

一方、3個のFFの中に極端に応答速度が遅いものが含まれていると、

どのようになるでしょうか？

例えば、初段のFFが遅いものとして、下の図を用いて説明しましょう。

　　�@　クロックの立ち下りにより、Q₀ はが 0 から 1 に変化する。

　　�A　Q₀が 1 になったため、NAND回路によりクリア信号（負論理）が 0 となる。

　　�B　Q₂ がクリアされ 0 となる。

　　　　　（1段目FFはクリア入力されるが応答速度が遅いため、Q₀は依然として 1 の状態）

　　�C　Q₂が変化したため、クリアが解除される（1となる）。

　　�D　クリア解除後に速度が遅いQ₀が 0 となり、

　　　　　　2段目のFFはこれをカウントして、Q₁ が 0 から 1 に変化する。

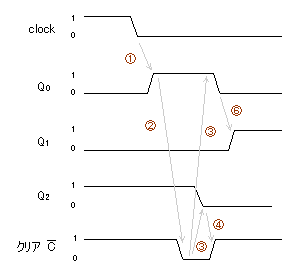
このように、本来（000）という状態にクリアされるカウンタが、 (010)という誤った状態にセットされてしまいました。

これが、いわゆる ハザードによる誤動作 です。

クロック周波数が高くなると、配線長による遅延時間などにより、 ハザードが発生する可能性があります。

論理回路の設計では、このようなハザードが絶対に生じないよう、 配慮しなければなりません。

4.2　D-FFを用いた5進カウンタ

非同期クリア入力のあるエッジトリガーD-FFを3個用いて、 5進カウンタを構成します。

その回路を以下に示します。

クロックの立ち上りで、D-FF出力を反転させますが、動作自体は、

4.1で説明したJK-FFによる5進カウンタと変わりありません。

上記回路でも、遅延時間の異なるFFを組み合せた場合には、

ハザードによる誤動作を生じさせる可能性があるので、注意が必要です。

５　まとめ

本章では、代表的な順序回路である 非同期式カウンタ について解説しました。

段数が多い非同期式カウンタは、クロック周波数が高くなると、 遅延時間が無視できなくなり、

ハザードを含む様々な問題が発生する可能性があります。

このため、一般には同期式のカウンタが使用されています。

次章では、この同期式カウンタの構成法について説明します。

論理回路2のトップページに戻る