
論理回路2
第3章 順序回路の基礎(その2)
-応用方程式と2進カウンタ-
井澤 裕司
1 はじめに
- 本章では、
応用方程式
を用いた順序回路の設計手法について解説します。
- 次に、
この手法を用いて、様々なフリップフロップを使用した1ビットの
2進カウンタ
の構成法を
紹介します。
2 応用方程式を用いた順序回路の設計手法
- 順序回路の設計手法
には様々なアプローチがありますが、 本章では
応用方程式
を用いた設計方法について紹介します。
- その手順は、以下のようになります。
- ① 設計する順序回路(例えば2進カウンタ)の
遷移表
を作成する。
- ② 求めた遷移表から
、応用方程式
に含まれる
変数 g1、g2
を、
入力(x)
を用いて表す。
- ③ 応用方程式の遷移表の関係を満たすよう、使用するフリップフロップの入力を決定する。
- その
入力方程式
の変数
g1、g2
に、②で求めた値を代入
する。
- ④ フリップフロップと③で求めた論理式に対応する組み合せ回路を用いて、
回路図
を作成する。
- なお、①と②は、設計する順序回路が決まれば、一意に決定されるものです。
- これに対し、③と④は、使用するフリップフロップに依存し、様々なバリエーションが表れます。
- ここで、”
応用方程式
”と”
フリップフロップの入力方程式
”という聞きなれない用語が出てきました。
- その内容について説明しましょう。
- 具体例として、1ビットの2進カウンタを、
RS-FF
を用いて設計します。
- ① 2進カウンタの遷移表の作成
- 1ビットの2進カウンタの遷移表は以下のようになります。

- 入力 x = 0 のとき、状態 Q は変化せず、x = 1で Q が反転します。
- ここで、現在の状態 Q がカウンタ出力に相当します。
- なお、出力の z は、2ビット目のフリップフロップ(FF)に接続して、
桁上げするための出力信号です。
- その使用法については、後ほど説明します。
- ② 応用方程式
- 応用方程式
とは、
次の状態
Qn
を
現在の状態
Q
と
入力
を用いて表現したものであり、一般に次のように表されます。
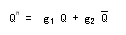
- この式で、
g1
、
g2
という変数は
0
または
1
の値をもつ
論理関数
です。
- g1、g2
は設計する順序回路に依存し、
その入力
の関数になります。
- 具体的な
g1
、
g2
と
順序回路の出力
z
は、①の
遷移表
から求めます。
- 1ビットの2進カウンタ
の場合、上の
遷移表
から、
応用方程式
は次のように表されます。
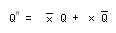
- これは、入力
x
が 0 のとき、
Qn
は
変化せず
(Qn=Q)、入力
x
が 1のとき、
Qn
は
反転
することを表しています。
- すなわち、入力
x
が 1 となる回数を計測する
2進数のカウンタ
(1ビット)に相当します。
- なお、2進カウンタの出力は
Q
です。
- また、
g1、g2
は入力 x を用いて、以下のように表せます。

- なお、クロックのある
JK-FF
や
D-FF
の場合、次のクロックの立ち上りで、2ビット目のFFを反転させるため、
- z = x Q
- という出力を用いることがあります。
- ③ 入力方程式の変数(g1、g2 )の決定
- 応用方程式
が決まると、この回路で使用する
フリップフロップ(FF)の種類
を決定し、その
入力方程式
を求めます。
- もう一度、
応用方程式
を示します。
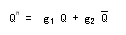
- この式で、出力
Qn
は、
g1、g2 および Q の関数
であり、これから下に示す
遷移表
が自動的に導かれます。
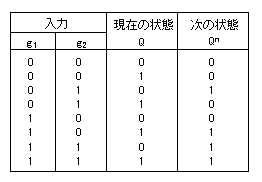
例えば
RS-FF
を選択した場合、その入力は、
S(セット)
と
R(リセット)
の2つです。- 前章
で説明したように、現在の状態
Q
から次の状態
Qn
への遷移を、
RS-FFの2入力
(R , S)
を用いて、
- 実現することを考えます。
- 上の
遷移表
の右半分にその結果を追加します。
- RS-FFの遷移表
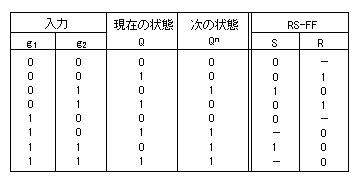
- 以下、簡単に補足します。
- 表の”
-
”は、
0または1のいずれでもよいことを示しています。
- 出力 Qが 0から1に変化するのは、入力のセット(S=1)が原因であり、
リセットはされていません(R=0)。
- 逆にQが 1から0に変化するのは、リセット(R=1)されたためであり、
セットはされていません(S=0)。
- なお Q = 0で変化しない場合は、セットもリセットもされなかったか、
リセットされたかのいずれかです。
- 同様に、Q = 1で変化しない場合は、セットもリセットもされなかったか、
セットされたかのいずれかです。
- この
遷移表
を用いて、
2つの入力
(R,S)をQと
g1、g2
を用いて表します。
- 入力S
に関する
カルノー図
を作成すると、以下のようになります。
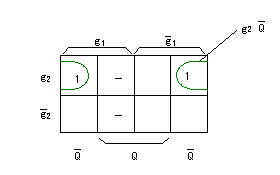
- また、
入力R
の
カルノー図
は以下のようになります。
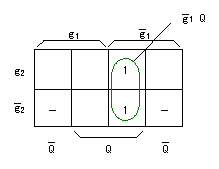
- これより、
RS-FFの入力方程式
が次のように定まります。
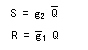
- この
入力方程式
は、FFの種類が決まれば自動的に定まる性質のものです。
- 次に、
入力方程式の g
1、g2
に、②で求めた関係式を代入します。
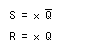
- ④ 回路図の作成
- ③で得られた FF の入力S, R の関係式から、回路図を作成します。
- 以下に
RS-FFを用いた2進カウンタ
の
回路図
を示します。
- なお、この回路図は、第2章で説明したT-FF(トグル フリップフロップ)を
RS-FFを用いて構成したものと同じです。
3 フリップフロップの入力方程式と2進カウンタ
- ここでは、
RS-FF以外
のフリップフロップ(FF)の
入力方程式
と
2進カウンタの構成法
について説明します。
- なお、本章では入力信号に使用上の制限がある
AC型のFF
(第2章参照)ではなく、
- 一般に広く用いられている
DC型
、あるいは、
クロック入力のあるエッジトリガー式
のFFである点に注意して下さい。
- 3.1 T-FF
- 手順①と②については、上で述べた
RS-FF
の場合と同じです。
- ③ 入力方程式
- T-FF
では、入力T=1で出力 Qが反転します。
- その
遷移表
を次に示します。
- T-FFの遷移表
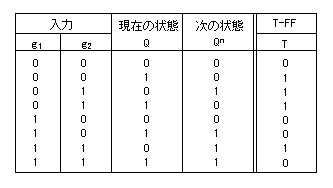
- これより、入力 Tを求めます。カルノー図は以下のようになります。
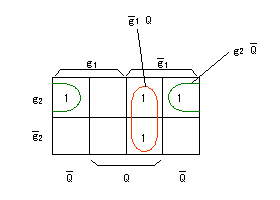
- これより、
T-FFの入力方程式
は以下のように求まります。
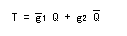
- この
g1、g2
に、②で求めた関係式を代入すると、以下のようになります。
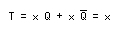
- ④ 回路図の作成
- 下に
T-FFを用いた2進カウンタ
の
回路図
を示します。
- なお、このT-FFは第2章で紹介した
パルス型(AC型)
ではなく、
- 入力 T の立ち上り直後に出力 Q が反転する
DC型のT-FF
であることに注意して下さい。
3.2 JK-FF
- 第2章で説明したように、
JK-FF
には、
クロック入力のない
タイプと、
クロック入力のある
タイプがあります。
- 一般には、入力信号に対する使用上の条件がない
クロック入力のある
JK-FFが広く用いられています。
- 入力 J と K の機能は、クロック入力のないタイプと同じですが、
- クロックの立ち下り(あるいは立ち上り)時点に
おける入力 J、K の状態により、
- セット、リセット、保持、反転等の動作を行います。
- このような、
エッジトリガーのJK-FF
を用いて、1ビットの2進カウンタを構成します。
- ① 2進カウンタの遷移表
- クロック入力のあるフリップフロップ
を使用し、遷移表を作成します。
- クロックが連続的に入力
される順序回路の場合、遷移表から
入力としてのクロックが省略される場合があります。
- 1ビットのカウンタの遷移表を以下に示します。

- すなわち、現在の状態
Q
を反転させたものが、次の状態
Qn
となります。
- ② 応用方程式
- エッジトリガーJK-FF
を使用した場合の
応用方程式
を求めます。
- クロック入力があるフリップフロップの場合、現在の状態
Q
を反転させたものが次の状態
Qn
となります。
- これより、
2進カウンタの応用方程式
は以下のように簡略化されます。
- g1 = 0
- g2 = 1
- 応用方程式
の中には、入力としてのクロックが明示的に示されていませんが、
- クロックの立ち上り(あるいは立ち下り)で、
出力 Q が
定常的に反転
していることに注意して下さい。
- ③ 入力方程式
- JK-FFでは、入力 J と K の機能は、RS-FFのS(セット)とR(リセット) とほぼ同じですが、
- J = K = 1で出力 Qが反転する点が異なります。
- これらを考慮して遷移表を作成すると、次のようになります。
- JK-FFの遷移表

- これより、入力 J, K を求めます 。
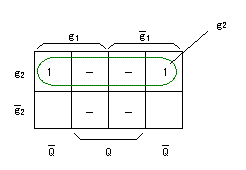
- まず、入力 J の
カルノー図
は以下のようになります。
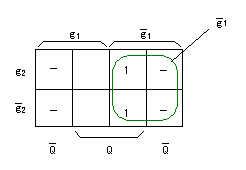
- 入力 K の
カルノー図
は以下のようになります。
- これより、
JK-FF の入力方程式
が得られます。
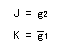
- 上式に、②の
応用方程式
の結果を代入すると、次の式が得られます。
- J = 1
- K = 1
- ④ 回路図の作成
- クロック入力のあるJK-FFを用いて、1ビットのカウンタを以下のように構成することができます。
- なお、このFFは、クロックの立ち下り時点の入力の状態で、
次の出力が決定するエッジトリガータイプです。
3.3 D-FF
- 第2章で説明したように、D-FFには、クロックの立ち上り時点の入力 D のみに出力が依存する
エッジトリガータイプ
と、
- クロックが 1 (すなわちH)のとき、入力 D が変化すると出力 Q も変化する、
ラッチタイプ
に分類されます。
- ここでは、エッジトリガーD-FFを用いて、2進カウンタを設計します。
- ① 2進カウンタの遷移表
- 遷移表は、クロック入力のあるJK-FFの場合と同じです。
- ② 応用方程式
- エッジトリガーD-FFを使用することを前提にして、
2進カウンタの応用方程式
を求めます。
- 結果は、JK-FFの場合と同じです。
- g1 = 0
- g2 = 1
- ③ 入力方程式
- クロック入力のあるD-FFには、2つの入力(D、クロック)があり、
- クロック立ち上り時点の入力Dの値が出力 Qに表れます。
- その遷移表を次に示します。
- D-FFの遷移表
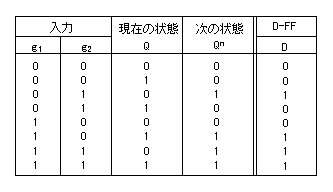
- ここで、入力 D のカルノー図は以下のようになります。
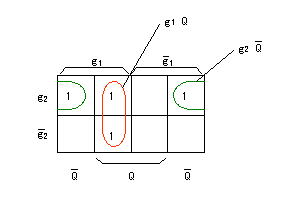
- これより、
D-FF の入力方程式
は以下のように求まります。
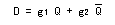
- この式は
応用方程式と同じ
表現になっていることに注意してください。 (
Qn = D
)
- すなわち、次の状態
Qn
を現在の状態
Q
を用いて生成し、これを入力
D
に接続すればよいことを示しています。
- ②で求めた、
g1、g2
を代入すると、次の式が得られます。
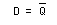
- クロック入力のある
エッジトリガーD-FF
は、実際の
同期式順序回路
で多用される
重要なフリップフロップ
です。
- その動作を十分理解し、設計に活用できるよう習熟して下さい。
- ④ 回路図の作成
- エッジトリガーD-FFを用いて、1ビットの2進カウンタを構成すると、以下のようになります。
- クロックの立ち上りで、出力 Q は反転します。
4 まとめ
- 本章では、順序回路の応用方程式とフリップフロップの入力方程式、
2進カウンタの構成法について解説しました。
- 次章では、より具体的なカウンタの構成法を説明します。
論理回路2のトップページに戻る

