論理回路２

第2章　順序回路の基礎（その１）

　　　－フリップフロップ－

井澤　裕司　　

本章では、 順序回路 の基本であるフリップフロップについて学習します。

「論理回路１」 で学んだ 「組合せ回路」 にはなかった、 時間の要素 が加わります。

タイムチャート 等、最初は慣れない項目があるかもしれませんが、 組合せ回路 の基本を復習すれば、十分理解できると思います。

1.1　順序回路とは

順序回路 とは、その時点の入力のみならず、 過去の入力信号 にも依存する回路です。

メモリ のように 内部状態 を 記憶 する機能が含まれていると考えて下さい。

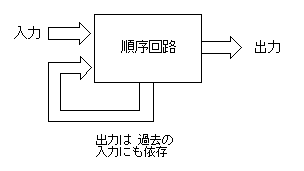
順序回路 の代表的なものは、この章の後半で説明する フリップフロップ ですが、

次章以降で説明する レジスタ や カウンタ 等も、この 順序回路 に属します。

なお、 順序回路 は、 組合せ回路 のように 真理値表 では、その動作を記述できません。

これにかわるのが 状態図 と 遷移表 です。

以下、その内容について説明しましょう。

ここでは、 状態図 と 遷移表 について解説します。

はじめに下の シーソー のような図を見てください。

現在は 右 側に重りが乗っており、 右 側が下がっています。

ここで、 左 側の Set というポイント（丸い印）を クリック して下さい。

今度は、 右 側の重りが消えて 左 側に移動すると同時に、 シーソー の 左 側が下ります。

次に、 右 側の Reset というポイントを クリック して下さい。

今度は、 左 側の重りが消え、 右 側に移動すると同時に、 シーソー の 右 側が下ります。

右 側が下がっているときに、 Reset を クリック しても シーソー の状態は変わりません。

また、左 側が下がっている場合の Set も同様です。

これは、 RSフリップフロップ という最も単純な 順序回路 の動作を表しています。

このような、 RS-FF の動作を次のような 状態図 というもので表すことができます。

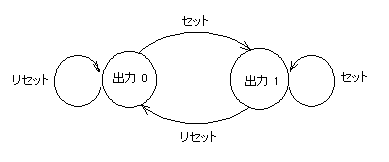
なお、ここでは シーソー の 右 側が上がった状態を、 出力１ と定義しています。

セット と リセット信号 により、出力は 0 と 1の間を遷移します。

この 状態図 から 遷移表 というものを作成します。

RS-FFの場合、以下のようになります。

　　　　RS-FFの遷移表

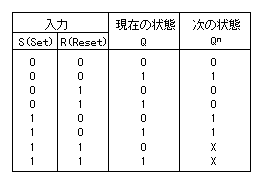
なお、入力の S(Set） と R(Reset） は重りを乗せた状態を１ と定義しています。

遷移表 の X は、2つの重りを シーソー の両端に同時に乗せる ことを 禁止 するという意味です。

同じ重りの場合 シーソー が釣り合ってしまい、出力は ０でも 1でもない状態となります。

これはもはや、論理回路ではありません。

この 遷移表 を作成することが、 順序回路 を設計する場合の原点になります。

これは、 組合せ回路 における 真理値表 と 同じ位置付けです。

1.3　まとめ

ここで、 順序回路 の一般的な 設計手順 を示しておきます。

① 遷移表 を作成する。

② 論理式 で表し、簡略化する。

③ 論理回路記号（MIL記号） で表す。

なお、②の簡略化については、 「論理回路１」 の 第5章 で述べた手法を用います。

次節では、これらの手順をいくつかの フリップフロップ回路 を例に説明します。

本節では、 フリップフロップ回路 （以下 FF とする）について説明します。

はじめに、その分類を示します。

①	RS-FF	（リセットセット フリップフロップ）
②	T-FF	（トグル フリップフロップ）
③	JK-FF	（JＫ フリップフロップ）
④	RST-FF	（リセットセットトグル フリップフロップ）
⑤	D-FF	（ディレイ フリップフロップ）

これらの動作上の違いを理解して下さい。

なお、次章で述べる レジスタ や カウンタ は、これらの フリップフロップ をベースに構成したものです。

この RSフリップフロップ は、すべての FFの基本 となるものです。

先に述べたように、リセットという入力が1になると、現在の状態に かかわりなく 出力は無条件に 0となります。

逆にセットという入力が 1になると、 出力は 無条件に 1になります。

入力がともに 0 であれば、その前の状態を保持します。

なお、2つの入力(R,S)は互いに矛盾するため、 これらが 同時に1になることは禁止されています。

以下に示す 遷移表 は、この RS-FF の動作を記述しています。

　　　　　RS-FFの遷移表

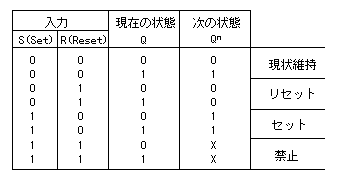
この 表から、次の状態 Q ⁿ を入力 ( S , R )と Q を用いて表します。

すなわち、現在の状態 Q は一種の入力とみなします。

この論理式を、 カルノー図 を用いて 簡略化 します。

結果を以下に示します。

（なお、 禁止 されている状態は × で表します。）

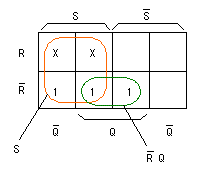
これより次の式が成立します。

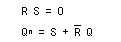
これらの式を 特性方程式 と呼びます。

1番目の式は、 リセット と セット が同時に1となる 状態を禁止するためのものです。

2番目の式についてその否定をとり、 ド・モルガンの定理 を用いて変形すると、次の式が得られます。

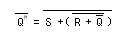
これより、 NOR回路 2個を用いて以下に示す回路図が得られます。

このように、 RS-FF は2入力の NOR回路 を用いて実現することができます。

この RS-FF の動作を示す タイムチャート を、以下に示します。

時間軸上での動作を十分理解して下さい。

次にこの回路を NAND回路 を用いて表現してみましょう。

上の論理式を変形すると次のような式が得られます。

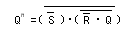
これより、以下の回路図が得られます。

入力の S と R が 負論理 となっている点に注意が必要です。

2.2　T-FF　（トグル　フリップフロップ）

この T-FF は、 トグル 、もしくは トリガーフリップフロップ の略で、入力 T の立ち上りで、出力 Q が反転します

この T-FF の 遷移表 は、以下のようになります。

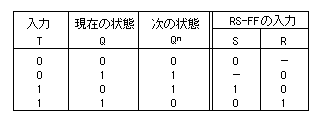
この表の左半分から論理式を求めます。

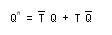
これらをMIL記号を用いて表現すると、以下に示す回路図（1番上）が得られます。

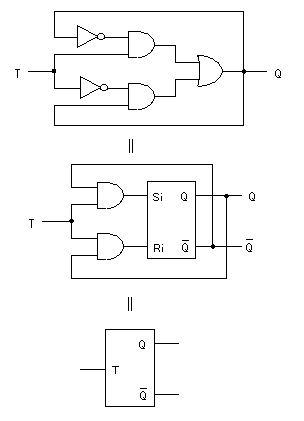
次に、上の 遷移表 の 右半分 を使用して、この T-FF を RS-FF を用いて構成する手法について説明します。

記号の 「－」 は、 0 と 1 の どちらでもよいことを示しています。

ここでは、 0 とみなすと、以下の式が得られます。

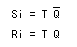
これより、上の中央の回路図が得られます。なお、この T-FF を簡略化した記号（図の下）で表すことがあります。

次に、この T-FF の タイムチャート を示します。

上の図で、入力信号 T = 1 の幅が狭いことに注意して下さい。

もし、 T = 1 の期間が長くなると出力 Q は 0 → 1 → 0 のように反転を繰り返し、 発振 します。

これを防ぐため、 T の立ち上り後、出力 Q が変化する前に T = 0 とする必要があります。

このような T-FF を、 パルス型T-FF（もしくはAC型T-FF） と呼びます。

このような、入力 T の制約をなくした T-FF を DC型T-FF と呼びます。

これらは、回路構成の違いにより (1)マスタ・スレーブタイプ と、 (2)エッジトリガータイプ に分類されます。

マスタ・スレーブタイプ の DC型T-FF の回路構成を以下に示します。

AC型T-FF に用いた ANDゲート と、 RS-FF の組み合せが2つ従属に接続されています。

前段が マスタ 、後段が スレーブ として動作します。

T=1 では 、 後段の出力を反転したものを前段のRS-FFに記憶し、 T=0 では前段出力を後段のRS-FFに転送します。

なお、出力 Q は T の立ち下り直後に反転します。

AC型のように反転出力を直接入力側に接続すると 発振現象 を起しますが、 このように2段構成で反転した信号の受け渡しを行うことにより、 入力 T の幅に依存しない 安定 な 反転動作 を実現しています。

エッジトリガータイプ の DC型T-FF の回路構成を以下に示します。

入力 T が接続する3入力NORの上下に、2入力のNORが1つずつ追加されています。

T=1 のとき、上と下のNOR出力で Qsbと Qrb は、 それぞれ not Q と Q を反転した値になります。

すなわち、T の立ち上りより少し遅れて、 Qsbは Q の値に、 Qrb は not Q の値にセットされます。

次に T=0 になった瞬間、中央の2つのNORが 、 Qsb と Qrb を入力とする RS-FF として動作します。

この出力 Qs、 Qrはそれぞれ後段のRS-FFのセット、リセット入力となっており、 T の立ち下りで出力 Q が反転します。

反転後、少し遅れて Qsbと Qrb はともに0に戻ります。

2.3　JK-FF　（JKフリップフロップ）

JK-FF は RS-FF に似ていますが、 J＝K＝1 で出力 Q が 反転 する点が異なります。

（ RS-FF では、 R＝S＝1 は禁止されていました。）

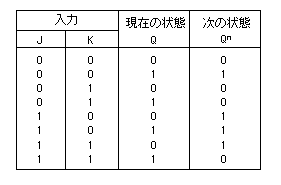
この JK-FFの遷移表 は、次のようになります。

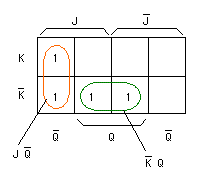
この遷移表から、以下の カルノー図 が得られます。

これより、簡略化された式が求まります。

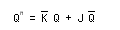
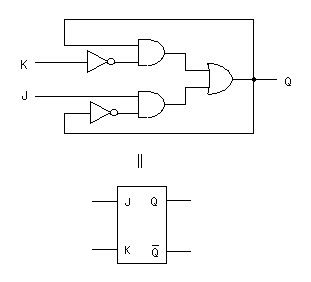
この式を MIL記号 を用いて表現すると、 次のようになります。

なお、この JK-FF を簡略化した記号（図の下）で表すことがあります。

次にこの JK-FF の タイムチャート を示します。

ここで示した ＪＫ-FF は クロックパルスのない タイプです。

2つの入力 J,K が同時にHになるとき、 出力 Q が反転しますが、

現実のハードウェアを用いて、 同時に変化する状態を作ることは極めて難しいことです。

一見同時に見えても、光が数十センチ進むような、 微小な時間を拡大して観測すると、

配線の長さなどにより わずかなずれを生じているためです。

この時間のずれを 過渡的ハザード と呼びます。

極めて高い信頼性が要求される論理回路では、 このハザードによる誤動作を防ぐ対策が必要になります。
そこで実際に用いられているのが、 クロックパルス のある JK-FF です。

その回路構成はやや複雑ですが、 興味のある人は、参考書等で確認して下さい。

2.4　RST-FF （リセットセットトグルフリップフロップ）

RST-FF は RS-FF に T-FF の機能が付加されたものです。

その 遷移表 を以下に示します。

なお表の” × ”は 禁止状態 を、” － ”は 0 と 1 のいずれでもよい ことを示しています。

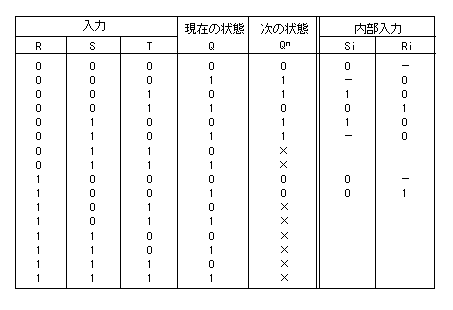
この表の左半分から、次の式が導かれます。

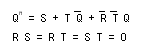
一方、この RST-FF を RS-FF を用いて実現する手法 について説明します。

上表の右半分に注目して下さい。

ここで記号の” － ”は 1と0のいずれでもよいことを示します。

例えば、上から2段目で出力 Q が1から 1となっていますが、 セット （ Si＝1 ）されたのか、あるいは セット も
リセッ トもされなかったのか のいずれかです。

しかし、リセット されたのではないことは明らかです。（ Ri＝0 )

ここで、 Si と Ri を R,S,T,Q を用いて表し、簡略化すると次式が得られます。

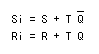
これより、 RST-FFの回路図と タイムチャートが得られます。

なお、この RST-FF も T-FF と同様、T=1の期間が長くなると、 出力 Q が発振するので注意が必要です。

D-FFの’ D ’は Delay の意味で、 1クロックの遅延素子 として使用されている最も重要な フロップフロップ です。

次章以降で説明するカウンタやレジスタを構成する基本的な FF ですので、 十分理解してください。

このD-FFの遷移表 は以下のようになります。

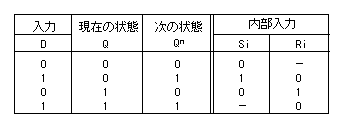
この D-FF を RS-FF を用いて実現します。

内部入力は、以下のように表されます。

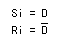
これより、次のような 回路図 と タイムチャート が得られます。

クロックパルスの幅が狭いことに注意して下さい。

上の回路の場合、クロックパルスがHの期間に入力 D が変化すると、 出力 Q も変化してしまいます。

（実際に、自分でタイムチャートを書いて確認して下さい。）

この回路は一般には、 ラッチ と呼ばれ、 エッジトリガーのD-FF と区別されています。

エッジトリガー とは、クロックの立ち上り時点における入力 D の値が、 次のクロックの立ち上りまで保存されるFFです。

すなわち、クロックの立ち上り以外で、入力Dが変化しても、出力Qは変化しません。

したがって、クロックパルスの幅などは自由に設定できます。

一般のLSI には、この エッジトリガー型D-FF が多用されていることを覚えておいて下さい。

3　まとめ

本章では、 順序回路 の基本となる フリップフロップ について学習しました。

次章では、この フリップフロップ を用いた カウンタ回路 について紹介します。

論理回路2のトップページに戻る