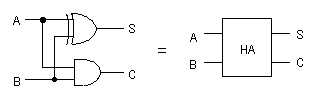第9章 組合せ回路(その2)
- 本章では、組合せ回路の代表的な応用例について解説します。
- 目次
- ・ セレクタとデマルチプレクサ
- ・ 半加算器と全加算器
- ・ 2進加算器
9.1 セレクタとデマルチプレクサ
- セレクタやデマルチプレクサは、複数の入力の中から
1つを選択して出力したり、
- 逆に1つの入力を複数の出力の1つに出力する機能があります。
- 本節では、その具体的な回路の実現法について紹介します。
9.1.1 セレクタ
- セレクタは、 マルチプレクサとも呼ばれ、多数の入力から
1つの入力を選択して出力する回路です。
- 入力の選択は、通常2進数に対応するセレクト入力により決定されます。
- 下図にその具体的な回路を示します。
- この回路では、8入力の中から1つを選択して出力します。
- A,B,Cは選択用の制御信号で、すべて0のとき入力のD0が、
すべて1のとき入力のD7が出力Zとなります。
9.1.2 デマルチプレクサ
- デマルチプレクサとは、セレクタとは逆の機能をもつ回路です。
- すなわち、1つの入力について複数の出力があり、
制御信号により1つの出力が選択されます。
- 下図にその回路を示します。
- この回路は、1入力 4出力であり、A,Bは選択用の制御信号で、
すべて0のとき入力が出力のZ0に、
- すべて1のとき出力のZ3に出力されます。
9.2 半加算器と全加算器
- 本節では、演算回路の基本となる加算回路を構成する要素
(半加算器、全加算器)について解説します。
9.2.1 半加算器
- 半加算器とは1ビットと1ビットの加算を行う回路です。
- 入力は2つ、出力はそのビット出力(Sum)と桁上り(Carry)の2つになります。
- 真理値表とその回路図は、次のようになります。
- なお、この半加算器は、しばしはHA(Half Adder)という略号で呼ばれ、
回路図で以下のように記述されることがあります。
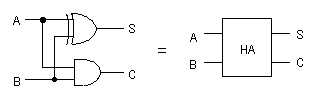
9.2.2 全加算器
- 全加算器も半加算器と同様、1ビットと1ビットの加算を行う回路ですが、
入力が3つあります。
- 3つ目の入力は、下の桁からの桁上りです。
- なお、出力はそのビット出力(Sum)と桁上り(Carry)の2つになります。
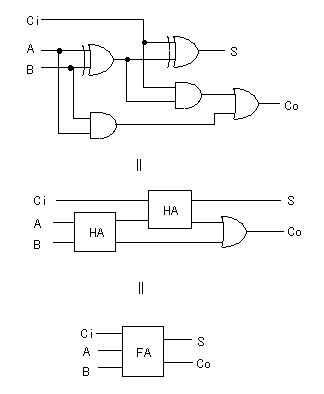
- 真理値表とその回路図は、次のようになります。
- この全加算器は、2つの半加算器と1つのOR回路を用いて構成することができます。
- なお、この全加算器は、しばしはFA(Full Adder)という略号で呼ばれ、
図のように記述されることがあります。
9.3 2進加算器
- 本節では、半加算器と全加算器を組み合わせた加算回路の構成法
について説明します。
9.3.1 2進加算器
- 正の2進数(4ビット)の加算を行う回路を以下に示します。
- LSBには半加算器(HA)、2~4ビットには全加算器(FA)を使用します。
- この回路では、桁上り(Carry)が下位から上位ビットに伝播するため、
ビット数が多くなると遅延時間が問題になります。
- このため、桁上り信号を別途高速に計算する手法がしばしば用いられます。
9.3.2 2進加減算器
- 2進(4ビット)加算と減算を行う回路を以下に示します。
- A1~A4,B1~B4はそれぞれ4ビットの正の2進数を表しており、
加算では、ビットのAs=0, Bs=0 とします。
- 一方、減算で例えばA-Bの場合はAs=0とし、引く方のビットBs=1とします。
- B-Aの場合はAs=1、Bs=0、-A-Bの場合は、As=1、Bs=1 です。
- 8個のEXOR(排他的論理和)は1の補数を生成するためのもので、
例えばAsが1のとき、A1~A4は1,0が反転します。
- 減算結果が負のとき、1の補数表示される点に注意して下さい。
- 2進数の値によっては、オーバーフロー(Overflow)が発生することがあります。
- このとき、これを示すビットが1になります。
論理回路1に戻る