論理回路は、大きく①組合せ回路と、②順序回路に分類することができます。

本章では、組合せ回路の概要と、基本的な回路の例について解説します。

目次

　8.1　論理回路の分類

　8.2　組合せ回路とは

　8.3　エンコーダとデコーダ

　8.4　文字表示回路

　8.5　演習問題

論理回路は大きく組合せ回路と順序回路に分類することができます。

① 組合せ回路

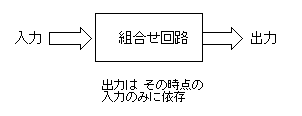
下の図に示すよう、 出力がその時点における入力の値の組合せにより定まる論理回路のことです。

② 順序回路

メモリのような内部状態を記憶する機能があり、 入力と内部状態の両方の値により、その出力が定まる論理回路。

一般には、一定の周期をもつクロックにタイミングを合わせて動作する 同期式 と、

そうではなく動作が終了すると直ちに次の動作へと進む 非同期式 に分類できます。

なお、第７章まで紹介してきた論理回路はすべて組合せ回路です。

順序回路については、第10章以降で説明します。

組合せ回路は、論理回路の基本であり、順序回路の中にも、
この組合せ回路が含まれています。

組合せ回路の一般的な設計手順を以下に示します。

　①　真理値表を作成する。

　②　論理式で表し、簡略化する。

　③　論理回路記号（MIL記号）で表す。

ここで、②の簡略化については、第5章で述べた手法を用います。

これから、代表的な組合せ回路について解説します。

本節では、エンコーダとデコーダ回路について説明します。

下にその概念図を示します。

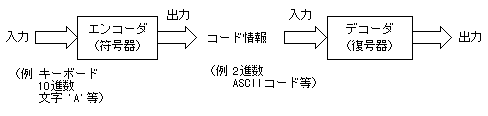
エンコーダとは、例えばキーボードの’Ａ’というアルファベットを、

計算機内部で使用するアスキーコード（ASCII）に変換する装置のことを指します。

一般には、人間が直接識別したりする情報を、 計算器が扱いやすい情報（符号）に変換するための装置（符号器）です。

一方、デコーダはこのエンコーダの逆の操作をする装置です。

エンコーダの例として、 10(8)進数を2進数に変換する回路について検討します。

ここでは、8入力（Z₇,Z₆,Z₅,...,Z₀）のいずれか 1つが 値 1をとるものとして、

それらの2進数に対応する3ビットの 出力（A₂,A₁,A₀）を生成する回路を考えます。

はじめに、真理値表を作成します。

次に、この真理値表から出力（A₂,A₁,A₀）の各々を、 8つの入力（Z₇,Z₆,Z₅,...,Z₀）を用いて表します。

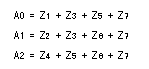
上の論理式は、これ以上簡略化することはできません。

これらの式をMIL記号を用いて表現すると、次に示す回路図が得られます。

デコーダの例として、 4ビットの2進数を10進数に変換する回路について検討します。

すなわち、入力（A,B,C,D）を2進数 について、その10進数に対応する 10個の出力（Z₀,Z₁,Z₂,...,Z₉） を出力する回路を考えます。

はじめに、真理値表を作成します。

次に、この真理値表から出力 （Z₀,Z₁,Z₂,...,Z₉）の各々を、 A,B,C,Dを用いて表します。

このとき、4ビットの入力（A,B,C,D）について、 10進数の10～15までの組合せが使用されていないことを利用して、 論理式をさらに簡略化することができます。

その結果を以下に示します。

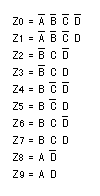
これらをMIL記号を用いて表現すると、以下に示すデコーダの回路が得られます。

10進数の10～15までは使用禁止のため、 入力（A,B,C,D）の値が10以上のとき、

出力の値が正しくならないことに注意して下さい。

液晶のディジタル時計等には、 下の図のような7つのセグメントからなる表示器が使用されています。

　図 バー セグメント表示器

4ビットの入力（A,B,C,D）を入力すると、 この2進数に対応する10進数（0～9）の数字が表示される回路について解説します。

この回路の真理値表は以下のようになります。

これらの出力について論理式を作成し、これを簡略化すると次の式が得られます。

なお、このとき4ビットの入力（A,B,C,D）について、 10進数の10～15までの組合せが使用されていないことを利用して、

さらに論理式を圧縮します。

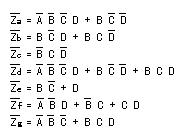
これらの論理式から、以下に示す文字表示回路が得られます。

この場合も、10進数の10～15までは使用禁止のため、入力（A,B,C,D）の値が10以上のとき、

出力値が正しくならないことに注意して下さい。

論理回路1に戻る