第7章 論理回路記号とその変換
- この章では、第3章で示した論理回路記号(MIL記号)について復習します。
- さらに、第4章の完全系で述べた回路の変換手法を一般化した
論理ゲートの等価変換の手法について解説します。
- 7.1 論理回路記号
- 7.2 論理ゲートの等価変換
- 7.3 演習問題
7.1 論理回路記号(MIL記号)
- 以下、基本的な7つの論理関数に対応する論理回路記号(MIL記号)について整理します。
- これらは第3章 論理関数(その1)の復習を兼ねています。
7.1.1 OR回路(論理和)
- OR回路(2入力)のMIL記号と真理値表を以下に示します。
- このORの入力数は2以上です。
7.1.2 AND回路(論理積)
- AND回路(2入力)のMIL記号と真理値表は以下のようになります。
- このAND回路も2入力以上です。
7.1.3 NOT回路(否定)
- NOT回路の真理値表とMIL記号を以下に示します。
- このNOT回路は1入力のみです。
7.1.4 NOR回路(否定論理和)
- 2入力のNOR回路のMIL記号と真理値表は以下の通ります。
- このNOR回路の入力数は2以上です。
7.1.5 NAND回路(否定論理積)
- NAND回路>(2入力)のMIL記号と真理値表は次の通りです。
- このNAND回路も2入力以上です。
7.1.6 XOR(EXOR)回路(排他的論理和)
- XOR(EXOR)回路の真理値表とMIL記号を以下に示します。
- 一般に、この回路の入力数は2です。
7.1.7 一致回路
- 一致回路の真理値表とMIL記号を以下に示します。
- この回路の入力数も2です。
7.2 論理ゲートの等価変換
- 第4章では、NORもしくはNAND回路は完全系を構成する方法について述べました。
- この完全系とは、それだけであらゆる論理回路が構成できる基本ゲートのことです。
- 以下任意の論理回路を、NORもしくはNANDだけの回路に変換する手法について解説します。
7.2.1 NAND回路への変換
- 与えられた論理回路(ゲート)にEXOR(XOR)回路が含まれている場合は、下の図に示すように、
- それらをANDやOR、NOT回路に変換します。
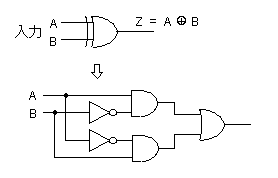
- なお一致回路も、最終段のOR回路をNOR回路に変更すればよいことになります。
- 次に、ORもしくはNOR回路を、ANDもしくはNAND回路に変換します。
- そのために、それらの入力にNOT回路を2つ従属に接続したものを挿入します。
- この二重否定を挿入しても、論理自体に変わりがないことは明らかです。
- さらに、次のド・モルガンの定理を用いて、否定入力のOR回路(NOR回路)をNAND回路に変換します。
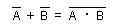
- 最後に、無駄な二重否定を整理すれば、求めるNAND回路 のみの論理回路が得られます。
- 以下、具体例を用いて説明します。
- [例]
- 次の論理回路をNAND回路のみを用いて表せ。
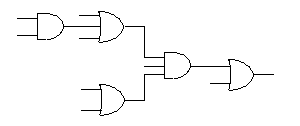
- [解]
- 3個のOR回路をNAND回路に変換するため、それらの入力に2重否定(①追加)を挿入します。
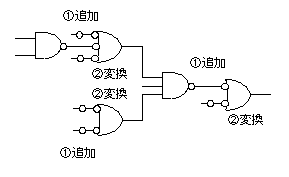
- 次に否定入力のOR回路をNAND回路に変換(②変換)すると、以下の回路が得られます。

7.2.2 NOR回路への変換
- 与えられた論理回路(ゲート)にEXOR(XOR)回路や
一致回路が含まれている場合は、前節と同様に、
- それらをANDやOR、NOT回路に変換します。
- 次に、ANDもしくはNAND回路を、ORもしくはNOR回路に変換します。
- 前節と同様に、それらの入力にNOT回路を2つ従属に接続したものを挿入します。
- この二重否定を挿入しても、論理自体に変わりがないことは明らかです。
- さらに、次のド・モルガンの定理を用いて、否定入力のAND回路(NAND回路)をNOR回路に変換します。

- 最後に、無駄な二重否定を整理すれば、求めるNOR回路のみの論理回路が得られます。
- 以下、その例を示します。
- [例]
次の論理回路をNOR回路のみを用いて表せ。

- [解]
- 2個のAND回路をNOR回路に変換するため、
それらの入力に2重否定(①追加)を挿入します。
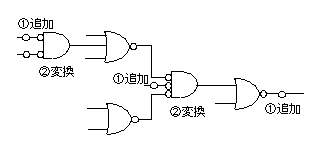
- 次に否定入力のAND回路をNOR回路に変換(②変換)します。
- なお、最終段のNOR回路の出力を反転するため、入力を接続したNOR回路を挿入しています。
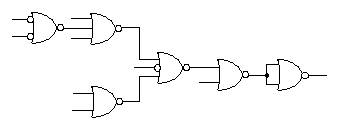
論理回路1に戻る
