第5章 論理関数(その3)
- 前章では、1つの真理値表に対応する論理式が数多く存在すること
を示しました。
- 本章では、それらの論理関数の中から、
最も簡略化された論理式を求める手法について学習します。
- はじめに、その準備として、最小項と最大項という用語について説明します。
- 次に、代表的な3つの簡略化手法を紹介します。
- 論理回路の1つの柱になる重要な手法ですので、
十分理解するよう努めてください。
目次
- 5.1 簡略化の準備(最小項と最大項)
- 5.2 簡略化手法(1) -Karnaugh図(カルノー図)
- 5.3 簡略化手法(2) -Quine法(クワイン法)
- 5.4 簡略化手法(3) -Quine-McCluskey法(クワイン-マクラスキー法)
- 5.5 演習問題
5.1 簡略化の準備(最小項と最大項)
- はじめに、簡略化の準備として、最小項と最大項という用語を定義します。
5.1.1 最小項と最大項
- 論理変数が3の場合の
最小項
と
最大項
を下の表に示します。
- 最小項
は3つの変数(A,B,C)の
論理積
の形で表され、
最大項
は逆に
論理和
の形になります。
- 0 と 1の関係が、最小項と最大項で逆になっている点に注目して下さい。
- なお、Venn図で明らかなように、最小項は分割された最小領域の1つに相当します。
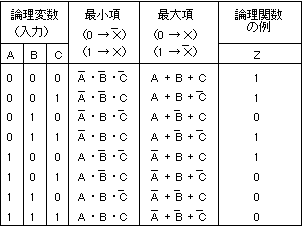
- 表の右欄に論理関数の例が示してあります。
- この値は最小項・最大項のように定まっておらず、
関数により変わりうることに注意して下さい。
- 論理関数を表す基本的な形式が2つあります。
- 最小項を使う形式と、最大項を用いる形式です。
- 表 3変数における最小項と最大項
5.1.2 最小項和表示(主加法標準展開)
- ここでは、最小項を用いる表示形式について解説します。
- 下のVenn図は上の表の関数 Z を表現しています。
- 全部で8つの領域があり、関数値が1の領域を緑色で示してあります。
- この部分の論理和をとると、関数 Z を表わすことができます。

- すなわち、以下の関係が成立します。
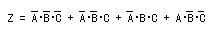
- このように与えられた関数を、最小項の論理和を用いて表現することを、
- 最小項和表示、
もしくは主加法標準展開
と呼びます。
5.1.3 最大項積表示(主乗法標準展開)
- 次に、最大項を用いて関数を表す形式について説明します。
- 下のVenn図を見てください。
- 図では全部で8つの領域があり、関数値が0の最大項を緑色で示してあります。
- この部分の論理積をとると、求める関数 Z になります。

- すなわち、以下の関係が成立します。

- このように、与えられた関数を最大項の論理積を用いて
表現することを、
- 最大項積表示
、もしくは主乗法標準展開
と呼びます。
5.2 簡略化手法(1) - Karnaugh図(カルノー図)
- はじめにカルノー図
について説明しましょう。
- その使用法については後で解説します。
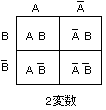
- 最も簡単な2変数のカルノー図
を以下に示します。
- 縦横2つ、計4個の区画(マス目)で構成されており、それぞれ
2つの変数 A,B の最小項に対応します。
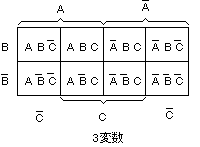
- 3変数のカルノー図
はマス目の数が8に増え、
以下のようになります。
- なお、区画を示す変数 A,B,C を入れ替えて、その位置が変わったしても、
- 最終的には同じ簡略化された論理式が導かれます。
- 4変数のカルノー図は以下の通りです。
- 区画(マス目)の数は24=16になります。

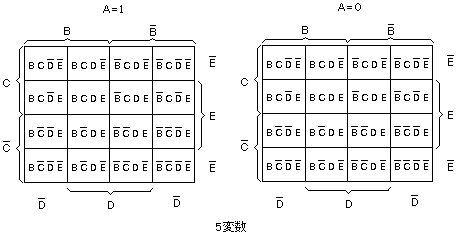
- 最後に、5変数のカルノー図
を示します。
- 区画(マス目)の数は25=32です。
- 4変数のカルノー図が上下に重なった形になっています。
- 次に、この
カルノー図の使用方法
について説明しましょう。
- カルノー図のマス目は、論理式の最小項に対応することはすでに述べましたが、
- ここに簡略化する論理関数の値 1 を書き込みます。
- 次に、これを2、4、8というループで囲みます。
- 以下、その具体的な手順を示します。
- [手順]
- (1) 論理関数を最小項の和で表す。
- (2) 各最小項に対応する区画(マス目)に1を記入する。
- (3) 1の区画を2のべき乗(例えば2、4、8、16)個で最大となるループで囲む。
- このとき以下の点に注意して下さい。
- ・図の上下・左右は巡回状に隣接しているものとする。
- ・ループは共通部をもってもよい。
- (4) 各ループに対応する項の和が簡略化された式となる。
- ただし、値 1 の最小項を最小限1つのループが囲んでいればよく、
- すべてのループの論理和をとる必要はない。
- これらの手順を例題を用いて説明しましょう。
- [例1] 2変数の場合
- 前章(第4章)の例題に示した関数 Z13
をカルノー図を用いて簡略化してみます。
- 真理値表より、カルノー図は次のようになります。
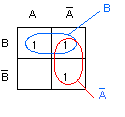
- この図より、簡略化された論理式が以下のように導かれます。
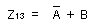
- [例2] 3変数の場合
- 3変数の例題として、次の論理式を簡略化します。
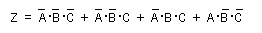
- このカルノー図は次のようになります。
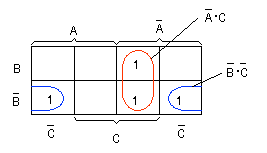
- 図より、以下のような最も簡略化された式が導かれます。
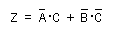
- [例3] 4変数の場合
- 4ビットの2進符号 ABCD は、正の2進数を表しており、
10進数の 0 から 9までの整数値をとるものとします。
- これらが、10進数で 4以下のとき値 0、5以上のとき値
1を
出力とする関数 Z
を求め、これを簡略化します。
- 2進符号の5,6,7,8,9に対応するマス目に値1を書き込むと、
次のようなカルノー図が得られます。
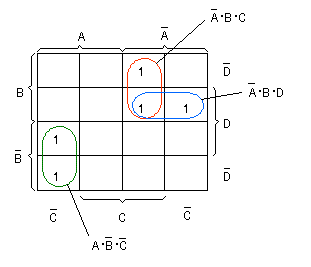
- これより、簡略化された論理式は次のように
なることがわかります。
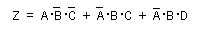
- [例4] 4変数で、冗長(禁止)入力がある場合
- 上の例題3では、
4ビットの2進符号 ABCD には、10進数の
10 から 15までの値は使用されていませんでした。
- このとき、これらの入力が禁止されているものとして、
論理式をさらに簡略化することができます。
- 上のカルノー図において、10進数の
10から 15までの値に
相当するマス目に
×
を記入します。
- この
×
は0と解釈しても
よいし、圧縮に利用できるのであれば 1と解釈しても
かまいません。
- この
×
を用いてさらに大きなループを構成します。
- 結果は、以下の通りです。

- これより、簡略化された論理式は次のようになります。
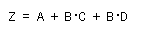
5.3 簡略化手法(2) -Quine法(クワイン法)
- カルノー図は直観的な手法ではありますが、必ずしも計算機向き
とはいえません。
- そこで、考案されたのが、Quineの手法です。
- その特徴は、以下の通りです。
- [特徴]
- ・ 算法が一定のため、多変数の場合に有利である。
- ・ コンピュータ処理に向いている。
- 次に、その手順を示します。
- [手順]
- (1) 与えられた論理式を最小項の和で表す。(主加法標準展開)
- [圧縮表の作成]
- (2) 各最小項を2進数の順に配列する。
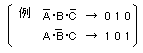
- (3) 各項を比較し、

- の形に簡略化する。(これを第1次圧縮という)
- (4) (3)の結果を2次以上について可能な限り繰り返す。
- [主項図の作成]
- (5) 主項(圧縮されずに残った項)を左に、最小項を上に書く。
- (6) 各主項が最小項を含むとき、その交点に○をつける。
- (7) 各最小項が少なくとも1つの○をふくむような、最も簡単な
主項の組み合わせを求める。
- 以下、例題を用いて具体的に説明します。
- [例1]
以下の論理式をクワインの手法により簡略化せよ。
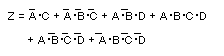
- [解]
- はじめに、上式を最小項の和で表します。
- なお、丸で示した数字は、対応する2進数です。
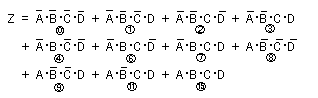
- 次に圧縮表を作成します。結果を以下に示します。

- この例では、第1次圧縮の項はすべて線で結ばれており、
最終的に残ったのは、第2次圧縮の6つの主項です。
- 次に、この主項を用いて主項図を作成します。
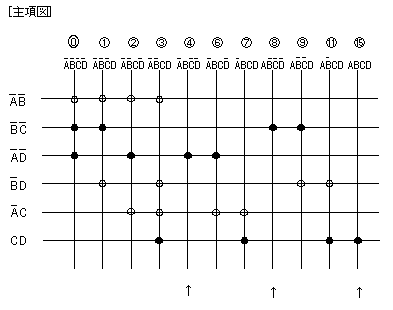
- 上向きの矢印(↑)は縦に1つしか○の付いていない最小項であり、
この項を含む主項を省くことはできません。
- このような、主項に含まれる最小項を黒丸(●)で表します。
- この例では、すべての最小項は少なくとも1つ以上、この黒丸(●)を
含んでいます。
- これより、簡略化された式は次のように求まります。

5.4 簡略化手法(3) -Quine-McCluskey法(クワイン-マクラスキー法)
- この手法は、先に説明したクワイン法の表記法を改良したものです。
- 以下に、その手順を示します。
- [圧縮表]における表現が多少変わっているだけです。
- [主項図]については、クワイン法 と同じです。
- [手順]
- (1) 与えられた論理式を最小項の和で表す。(主加法標準展開)
- [圧縮表の作成]
- (2) 各最小項を2進数の順に配列する。
- (3) 各項を比較し、距離1の符号(対応するビットで異なるものが1つ)を選ぶ。
- 例えば、0011 と
0111 は、 0 11 のように圧縮し、
圧縮した項は、チェックマーク(レ)を付ける。
- (4) (3)の結果を2次以上について可能な限り繰り返す。
- [主項図の作成]
- (5) ~ (7) はクワインの手法と同じ。
- [例2]
上記クワインの例と同じ論理式
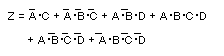
- をクワイン・マクラスキーの手法を用いて簡略化せよ。
- [解]
- はじめに圧縮表を作成します。
- 結果は以下の通りです。

- 主項図以下はクワインの手法と同じです。
論理回路1のトップページに戻る
