第４章 論理関数（その２）
- 本章では、１つの真理値表に対応する論理式が無数にあることを示します。
- 次に、それらの式を変形する規則をまとめたブール代数について学習します。
目次
- 4.1 論理式の変形
- 4.2 ブール代数の基本公式
- 4.3 完全系について
- 4.4 演習問題
4.1 論理式の変形
- 前章では、基本的な7つの論理関数について学びました。
- それらを入力数で分類すると、次のようになります。
- ・
1入力 ：
否定
- ・
主に2入力 ：
排他的論理和、一致
- ・
2入力以上 ：
論理和、論理積、否定論理和、否定論理積
- それでは、２つの入力をもつ関数を分類してみましょう。
- はじめに2入力関数の真理値表を作成します。
- 下表の左側に結果を示します。表を見やすくするため、
入力 A, B や関数の値を横方向 に書いている点に注意して下さい。
- （これまでの真理値表では縦書きでした。）
- この入出力の関係は、全体で２の４乗、すなわち
16通り
存在します。
2入力論理関数の分類
.gif)
- 表の右側に、代表的な論理関数（論理式）とその名称を示します。
- 重要なことは、論理式（論理回路）の表し方は必ずしも１通りではないという点です。
- すなわち、同じ論理を表す回路（式）は無数にあり、工学の観点からすれば、
- それらの中から最もシンプルな回路（すなわち論理式）を求めることが重要になります。
- （その手法については、第５章で学習します。）
- 例として、例えば上図の
Z13
について調べてみましょう。
- 以下に、この関数の真理値表を示します。
Z13
の真理値表
論理変数
（入力）
|
論理関数
（出力）
|
|
Ａ
|
Ｂ
|
Ｚ
|
０
０
１
１
|
０
１
０
１
|
１
１
０
１
|
- この真理値表のVenn図は下の通りです。
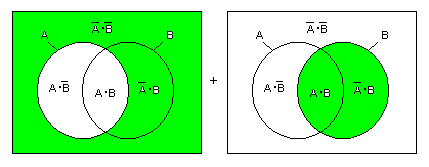
- 上の論理式 Z13 は以下に示すように、2つの領域の論理和として解釈することができます。
- ここで真理値表の出力の１に着目して下さい。
- この表で、出力が
1
となるのは、
- (A = B = 0) または (A = 0, B = 1) または(A = B = 1)
- の３つの場合です。
- この関係をVenn図で表わしてみましょう
- これより、Z13 は上の3領域の論理和 (OR) により表せることがわかります。
- すなわち、以下の式が成立します。
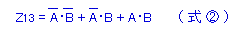
- 次に、上の図の左と中央の２領域を１つにまとめます。
- この場合のVenn図は次のようになります。
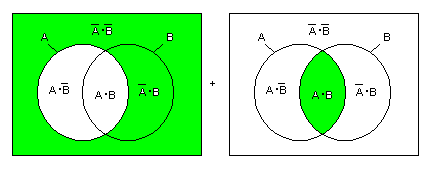
- これより、以下の式が成立します。
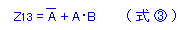
- それでは、中央と右の２領域を１つにまとめると、どのようになるでしょうか？
- この場合のVenn図は次のようになります。
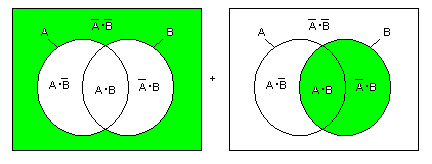
- これより、以下の式が成立します。
- もう一度上の真理値表に戻ります。
- 今度は出力の1ではなく、０に着目します。
- その領域は、次のようになります。
- この領域を表す関数の否定をとれば、もとの関数そのものを表すことになります。
- これより、以下の論理式が導かれます。
- このように、一つの真理値から無数の論理関数が導き出せることがわかります。
- 次に、式①の回路と、式②の回路をMIL記号を用いて表現してみましょう。
- はじめに式①の回路です。
- 次に式②の回路です。
- 式①の回路の遅延は2段で、必要な論理素子はNOTとORが各１個です。
- ところが式②の回路の遅延は3段となり、素子はNOTが2個、ANDが2個、ORが1個です。
- これらは、同じ論理を実現するのですが、①の方が高速で素子数も2／5（40%）と少なくなっています。
- 論理回路を設計するとき、どちらの回路を選ぶべきか、答は明らかです。
4.2 ブール代数の基本公式
- 真理値表はただ1通りの表現しかないのに対し、論理回路や論理式の表し方は１通りではなく、
様々な表現を取り得ます。
- ブールはその式を変形する規則について研究し、
これ以上簡単にはならない８つの公式で表すことができることを最初に明らかにしました。
- 以下に、その規則を示します。
- 表 ブール代数の規則
- 直観的に正しいといえる規則がほとんどですが、中には少し疑問が残るものもあります。
- 例えば、分配則やド・モルガンの定理です。
- これについて、以下検証してみましょう。
- 分配則のチェック
- (1) A･(B＋C)＝A･B＋A･C
- これについて、以下検証してみましょう。
- 左辺はVenn図を用いると、以下のようになります。
- 次に右辺は次のようになります。
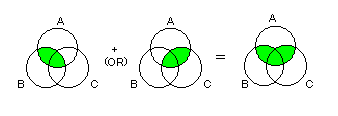
- これより、上式の正しいことが証明できました。
- (2) A＋(B･C)＝(A＋B)･(A＋C)
- 左辺はVenn図を用いると、以下のようになります。
- 次に右辺は次のようになります。
- これより、上式の正しいことが証明でき、分配則の正しいことが明らかになりました。
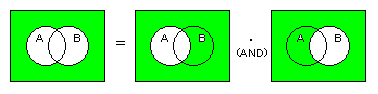
- ﾄﾞ・モルガンの定理のチェック
- (1)
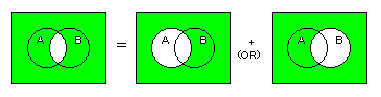
- 下にVenn図を示します。これより、上式が正しいことが明らかです。
- (2)
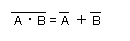
- 以下のVenn図より、この式の正しいことがわかります。
4.3 完全系について
- 任意の論理関数は、
NOR（否定論理和）
、もしくは
NAND（否定論理積）
だけで構成することができます。
- このとき、NOR（もしくはNAND）は
完全系を構成する
という表現を用います。
- 以下、いくつかの実例により、このことが正しいかどうか確認してみましょう。
4.3.1 NOT→ NOR
- はじめに NOT を NORのみ で表現します。
- NOT回路はMIL記号で表すと、以下のようになります。
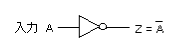
- NOR回路の入力を１つにまとめると、NOTと同じ機能になります。
- （真理値表で確認してみてください。）
- 下の図のように、2つの入力のうち１方を ０ に固定しても同じ論理となります。
4.3.2 NOT→ NAND
- 次に NOT を NANDのみで表現してみましょう。
- NAND回路の入力を１つにまとめると、NOTと同じ機能になります。
- （真理値表で確認してみてください。）
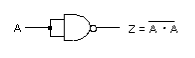
- 下の図のように、2つの入力のうち１方を 1 に固定しても同じ論理となります。
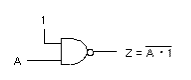
4.3.3 OR→ NOR
- 今度は OR を NORのみで表現してみましょう。
- はじめにOR（2入力）回路を示します。
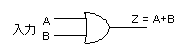
- 次に、その出力にNOTを2つ追加します。
- （その追加により論理関数自体は変化しないことは明らかです）
- 次に、ORと1段目のNOT回路を統合し、2段目のNOTをNORで表します。
- これで、ORが2つのNORにより表現できました。
4.3.4 OR→ NAND
- 次に同じ OR を NAND のみで表してみましょう。
- 4.3.3 の場合と同様に、出力に NOT を2つ追加します。
- 次に、ﾄﾞ・モルガンの定理を用い、OR と1段目の NOT 回路を変更します。
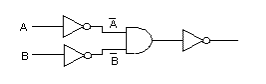
- ここで、2つのNOTを NAND で表し、AND とその出力の NOT を1つのNANDに変換します。
- これで、OR が3つの NAND により表現できました。
4.3.5 AND → NAND
- 今度は、AND を NANDのみで表現してみましょう。
- はじめにAND（2入力）回路を示します。
- これまで場合と同様に、出力に NOT を2つ追加します。
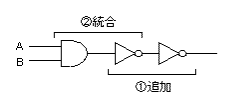
- 次に、AND と1段目のNOT回路を統合し、2段目のNOTをNANDで表します。
4.3.6 AND→ NOR
- 次に ANDを NORのみで表現してみましょう。
- 4.3.5 の場合と同様に、出力に NOT を2つ追加します。
- 次に、ﾄﾞ・モルガンの定理を用い、AND と1段目の NOT回路を変換します。
- ここで、2つのNOTを NOR で表し、OR とその出力の NOT を1つのNORに変換します。
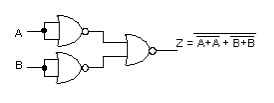
- これで、ANDが3つのNORにより表現できました。
- 以上、NOR、もしくはNAND回路があれば、どのような論理回路でも設計できる
ことが、わかったと思います。
- このような、回路の変換は実際の設計で用いることがありますので、十分理解してください。
4.4 演習問題
- 本章では、ブール代数について学習しました。
- これらの内容を十分理解するためには、問題を解くのが効果的です。
- 次の演習問題（全7問）を解き、十分理解してください。
演習問題[4]に進む