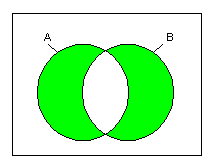第3章 論理関数(その1)
- すべてのディジタル回路は、基本的な論理関数の組み合せにより構成されています。
- 本章では、代表的な7つの論理関数について学習します。
目次
- 3.1 論理関数とは
- 3.2 真理値表と論理式
- 3.3 基本的な論理関数
- 3.4 演習問題
3.1 論理関数とは
- はじめに、論理関数という用語について定義します。
- 論理関数は
1
または
0
の値をもち、 以下のような関係があります。
- 論理関数 :
Z=F(A,B,C,…)
- ここで、
A,B,C
は
論理変数
と呼び、
これも
1
または
0
の値をとります。
- 一般の記号論理学では
1
が
真
、
0
が
偽
となります。
- 論理回路では、
1
が
High(例えば5V)
,
0
が
Low(0V)
です。
- 下の図を見てください。
- ランプと3つのスイッチ、電池で構成された回路です。
- (スイッチをマウスでクリックすると、ON、OFFと変化しますので、操作してください。)
- ランプが点灯するのは、どのような場合でしょうか?
- 2つのスイッチ
A
,
B
が並列に接続され、これと直列にスイッチ
C
が接続されています。
- 答は、
A
,
B
の少なくとも1方が
ON
で、スイッチ
C
が
ON
の場合です。
- これを真理値表という形で表現すると、図の右のようになります。
- ここで、スイッチの
ON
状態は
1
、
OFF
は
0
で表しており、ランプが点灯した状態が
1
、消えた状態は
0
となっています。
3.2 真理値表と論理式
- 上の図では、スイッチの接続関係を見れば、その間の論理関係を導くことが可能でした。
- しかし、もっと複雑な回路の場合は、その論理関係を導くことはそれほど簡単ではありません。
- 一般に、新たな論理回路を設計する場合、最初に行うことはその動作を記述する
真理値表
を作成することです。
- 次に、この論理を式(論理式)で表し、簡略化するという手順をとります。
- 真理値表はただ1通りであるのに対し、論理式や実際の回路は様々な形をとることに注意して下さい。
- 論理式を表現する記号として、
+(プラス、またはオア)
や
・(ドット、またアンド)
を用います。
- 次節では、代表的な論理関数の表現法について学習します。
- 真理値表と論理式の関係について十分理解を深めて下さい。
3.3 基本的な論理関数
- 以下、基本的な論理関数を7つ挙げ、その真理値表とVenn図を示します。
- それぞれの違いに注目して、各関数の
チェック
をクリックしてください。
- (入出力のボタンや真理値表の一部をクリックすると、1と0が反転します。)
3.3.1 論理和(OR)
- Z=A+B (2入力)
- Z=A+B+C (3入力)
OR の真理値表
|
論理変数
(入力)
|
論理関数
(出力)
|
|
A
|
B
|
Z
|
|
0
0
1
1
|
0
1
0
1
|
0
1
1
1
|
OR の Venn図

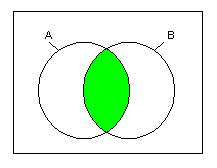
3.3.2 論理積(AND)
- Z=A・B (2入力)
- Z=A・B・C (3入力)
AND の真理値表
|
論理変数
(入力)
|
論理関数
(出力)
|
|
A
|
B
|
Z
|
|
0
0
1
1
|
0
1
0
1
|
0
0
0
1
|
AND の Venn図
3.3.3 否定(NOT)

NOT の真理値表
|
論理変数
(入力)
|
論理関数
(出力)
|
|
A
|
Z
|
|
0
1
|
1
0
|
NOT の Venn図

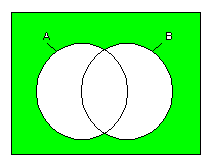
3.3.4 否定論理和(NOR)
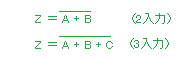
NOR の真理値表
|
論理変数
(入力)
|
論理関数
(出力)
|
|
A
|
B
|
Z
|
|
0
0
1
1
|
0
1
0
1
|
1
0
0
0
|
NOR の Venn図
3.3.5 否定論理積(NAND)
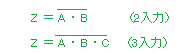
NAND の真理値表
|
論理変数
(入力)
|
論理関数
(出力)
|
|
A
|
B
|
Z
|
|
0
0
1
1
|
0
1
0
1
|
1
1
1
0
|
NAND の Venn図
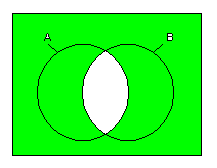
3.3.6 排他的論理和(XOR)

XOR の真理値表
|
論理変数
(入力)
|
論理関数
(出力)
|
|
A
|
B
|
Z
|
|
0
0
1
1
|
0
1
0
1
|
0
1
1
0
|
XOR の Venn図
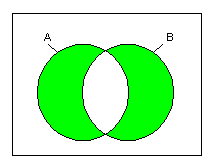
3.3.7 一致(Inclusive AND)

一致 の真理値表
|
論理変数
(入力)
|
論理関数
(出力)
|
|
A
|
B
|
Z
|
|
0
0
1
1
|
0
1
0
1
|
1
0
0
1
|
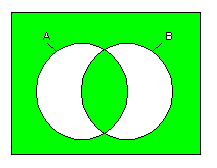
一致 の Venn図
論理回路1に戻る