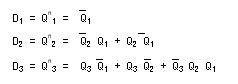11.1.1 順序回路の設計手順
順序回路の設計手法にはいくつかのアプローチがありますが、ここでは、応用方程式を用いた方法について紹介します。
この応用方程式とは、次の状態 Qnを現在の状態 Q と入力で
表現したもので、一般に次のように表されます。
![]()
この式で、g1、g2という変数は0または1の値をもち、
具体的には順序回路の入力の関数になります。
これらg1、g2と順序回路の出力(Z)は遷移表から求めます。
カルノー図等の手法により簡略化します。
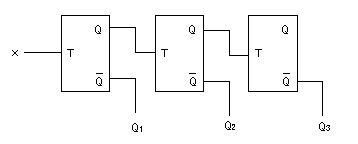
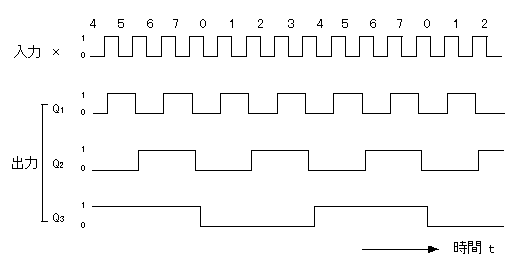
例えば、この後で述べる2進カウンタ(1ビット)の場合は
1入力(変数: x)であり、
![]()
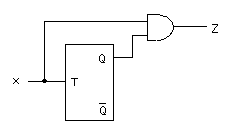
の関係が成立します。 また、2進カウンタの出力 Z は
Z = x Q
と表されます。
なお、この具体的な求め方については、次節で説明します。
次に、この順序回路で使用するフリップフロップ(FF)の種類を決定します。
例えばRS-FFを選択した場合、そのFF入力は、
S(セット)とR(リセット)の2つであり、その入力方程式は次のようになります。
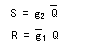
この入力方程式は、FFの種類が決まれば自動的に定まる性質のものです。
なお、その求め方については、このあと説明します。
2進カウンタの場合、上で求めたg1、g2を代入すると以下のようになります。

この式から、RS-FFを用いた2進カウンタの回路図が次のように求まります。
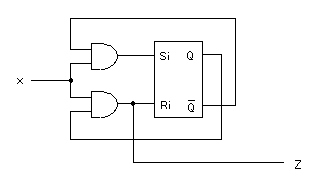
以上の手順を整理すると、次のようになります。
① 入力(x)と出力(Z)に関する遷移表を作成する。
② 応用方程式のg1、g2と出力(Z)を入力(x)を用いて表し、簡略化する。
③ 使用するフリップフロップ(FF)の入力方程式に②で求めたg1、g2を代入する。
④ ③の結果と出力の式から論理回路を構成する。
11.1.2 フリップフロップの入力方程式
ここでは、フリップフロップ(FF)の入力方程式について解説します。もう一度、応用方程式を示します。
![]()
これより、下に示す遷移表が自動的に導かれます。

① RS-FF
はじめに、RS-FFの入力方程式を求めます。第10章で説明したように、現在の状態 Qから次の状態 Qn
への遷移を、RS-FFの2入力(R,S)を用いて、実現することを考えます。
遷移表の右半分にその結果を追加します。
- RS-FFの遷移表
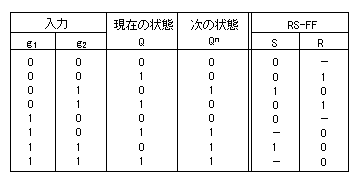
表の”-”は、0または1を示します。 以下、簡単に説明します。
出力 Qが 0から1に変化するのは、入力のセット(S=1)が原因であり、
リセットはされていません(R=0)。
逆にQが 1から0に変化するのは、リセット(R=1)されたためであり、
セットはされていません(S=0)。
なお Q = 0で変化しない場合は、セットもリセットもされなかったか、
リセットされたかのいずれかです。
同様に、 Q = 1で変化しない場合は、セットもリセットもされなかったか、
セットされたかのいずれかです。
この遷移表を用いて、2つの入力(R,S)をQとg1、g2を用いて表します。
入力Sに関するカルノー図を作成すると、以下のようになります。
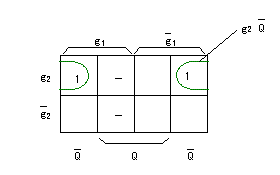
また、入力 Rのカルノー図は以下のようになります。

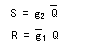
② T-FF
T-FFでは、入力T=1で出力 Qが反転します。その遷移表を次に示します。
- T-FFの遷移状
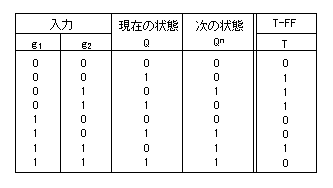
これより、入力 Tを求めます。カルノー図は以下のようになります。

これより、T-FFの入力方程式は以下のように求まります。
![]()
③ JK-FF
JK-FFでは、入力JとKの機能は、RS-FFのS(セット)とR(リセット)とほぼ同じですが、J = K = 1で出力 Qが反転する点が異なります。
これらを考慮して遷移表を作成すると、次のようになります。
- JK-FFの遷移表

これより、入力 J, K を求めます。
まず、入力 J のカルノー図は以下のようになります。

入力 K のカルノー図は以下のようになります。

これより、JKーFF の入力方程式が得られます。
④ D-FF
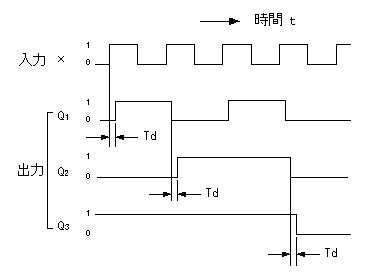
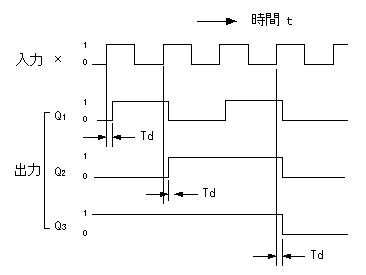
D-FFには2つの入力(D、クロック)があり、入力Dの値が1クロック遅延して出力 Qにあらわれます。
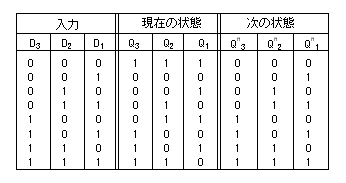
その遷移表を次に示します。
- D-FFの遷移表
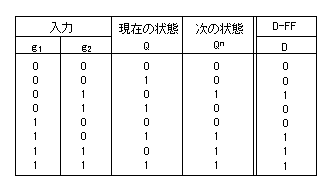
ここで、入力 D のカルノー図は以下のようになります。
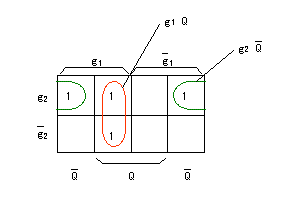
これより、DーFF の入力方程式は以下のように求まります。
![]()
この式は応用方程式と同じ表現になっていることに注意してください。
(Qn = D)
すなわち、次の状態 Qn を現在の状態 Q を用いて生成し、これを入力
D に
接続すればよいことを示しています。
このD-FFは、実際の同期式順序回路で多用される重要なフリップフロップ(FF)です。
その動作を十分理解し、設計に利用できるようになることが望まれます。