
なお、シーソーの右側が上がった状態を、出力1と定義しています。
セットとリセット信号により、出力は 0 と 1の間を遷移します。
この章の後半で説明するフリップフロップがその代表的なものですが、
次章以降で説明するレジスタ・カウンタも、この順序回路に属します。
なお、順序回路は、組合せ回路のように真理値表では、
その動作を記述できません。これにかわるのが状態図と遷移表です。
以下、その内容について解説します。
このような、RS-FFの動作を次のような状態図というもので
表すことが可能です。

なお、シーソーの右側が上がった状態を、出力1と定義しています。
セットとリセット信号により、出力は 0 と 1の間を遷移します。
この状態図から遷移表というものを作成することが可能です。
その例を以下に示します。
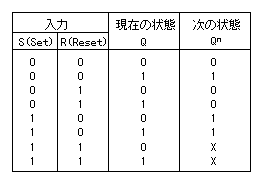
この遷移表を作成することが、順序回路を設計する場合の
原点になります。これは、組合せ回路における真理値表と
同じ位置付けです。
ここで、順序回路の一般的な設計手順を示しておきます。
① 遷移表を作成する。
② 論理式で表し、簡略化する。
③ 論理回路記号(MIL記号)で表す。
なお、②の簡略化については、第5章で述べた手法を用います。
次節では、これらの手順をいくつかのフリップフロップ回路を例に
解説します。
以下に示す遷移表は、このRS-FFの動作を記述しています。
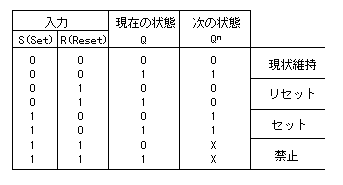
この表から、次の状態Qn を求めます。
上の表から、次の状態Qn を入力(S,R)とQを用いて表します。
すなわち、現在の状態 Q は一種の入力とみなします。
この論理式を、カルノー図を用いて簡略化します。
結果を以下に示します。
(なお、禁止されている状態は×で表します。)

これより次の式が成立します。
![]()
これらの式を特性方程式と呼びます。
1番目の式は、リセットとセットが同時に1となる
状態を禁止するためのものです。
2番目の式についてその否定をとり、ド・モルガンの定理を用いて
変形すると、次の式が得られます。
![]()
これより、NOR回路2個を用いて以下に示す回路図が得られます。
![]()
これより、以下の回路図が得られます。
入力のSとRが負論理となっている点に注意が必要です。
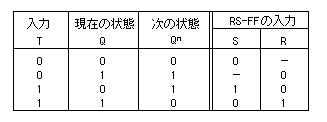
この表の左半分から論理式を求めます。 結果は次のようになります。
![]()
これらをMIL記号を用いて表現すると、以下に示す回路図(1番上)が
得られます。
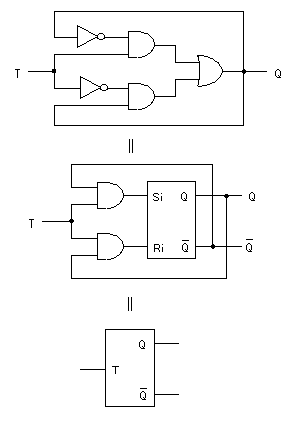
次に、上の遷移表の右半分を使用して、このT-FFをRS-FFを用いて
構成する手法について説明します。
記号の「-」は、0と1のどちらでもよいことを示しています。
ここでは 0とみなすと、以下の式が得られます。
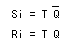
これより、上の中央の回路図が得られます。
なお、このT-FFを簡略化した記号(図の下)で表すことがあります。
次にこのT-FFのタイムチャートを示します。
このような、入力Tの制約をなくしたT-FFをDC型T-FFと呼びます。
ここで説明するスペースがありませんので、その内容については
参考書等で勉強して下さい。
この遷移表は、次のようになります。

この遷移表から、以下のカルノー図が得られます。
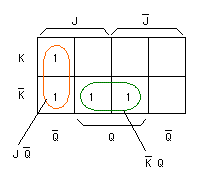
これより、簡略化された式が求まります。
![]()
この式をMIL記号を用いて表現すると、
次のようになります。
なお、このJK-FFを簡略化した記号(図の下)で表すことがあります。

そこで考え出されたのが、クロックパルスのあるJK-FFです。
その回路構成はやや複雑です。興味のある人は、参考書等で
確認して下さい。
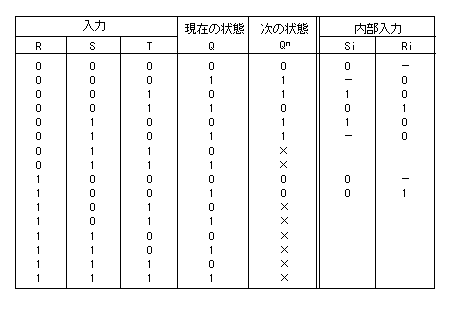
この表の左半分から、次の式が導かれます。
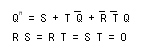
一方、この RST-FFを RS-FFを用いて実現する手法
について説明します。
上表の右半分に注目して下さい。
ここで記号の”-”は 1と0のいずれでもよいことを示します。
例えば、上から2段目で出力 Qが1から 1となっていますが、
セット(Si=1)されたのか、あるいはセットもリセットもされなかったのか
のいずれかです。しかし、リセットされたのではないことは明らかです。(Ri=0)
ここで、Si と Ri を R,S,T,Q を用いて表し、簡略化すると次式が得られます。
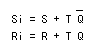
これより、次の回路図が導かれます。

最後にこのRST-FFのタイムチャートを示します。
なお、このRST-FFもT-FFと同様、T=1の期間が長くなると、
出力 Qが発振するので、注意が必要です。
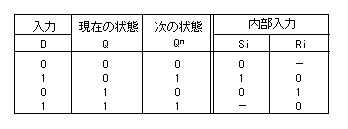
この D-FF を RS-FFを用いて実現します。
内部入力は、以下のように表されます。
![]()

最後に、このD-FFのタイムチャートを示します。