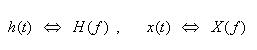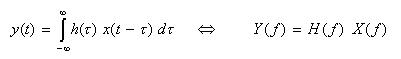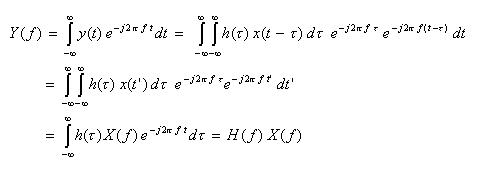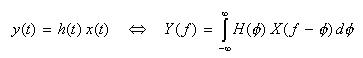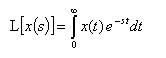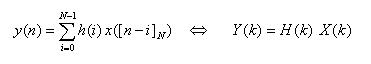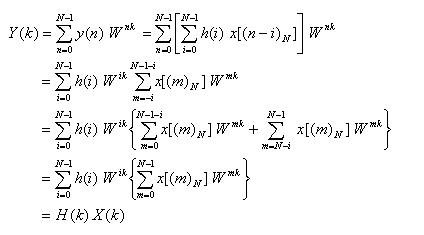線形システム
井澤 裕司
1. 線形システムとは
- これまでは、様々な信号とこれに対応するスペクトルの関係を中心に検討してきました。
- 本章では、
「線形システム」とその特性
について学習します。
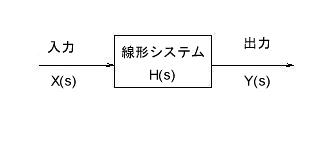
- この線形システムには入力と出力があり、それらの間には一定の関係が存在します。
- 本章の目的は、入力と出力の信号波形やスペクトルとの関係を明らかにすることです。
- 線形システムの特性が記述できれば、入力信号から出力信号を計算により求めたり、
- 逆に出力からその入力を計算することも可能です。
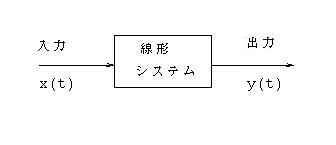
- ここで扱う
「線形システム」
は、正確には
「線形時不変システム」
です。
- (以下、単純に「
線形システム
」とします)。
- 連続信号における線形時不変システムの定義は、以下の通りです。
- (1) 線形システム
- 入力
x1(t), x2(t)
出力
y1(t), y2(t)
について
- x1(t) → y1(t), x2(t) → y2(t)
- の関係が成立するとき、任意の定数を
a, b
として、
- a x1(t) + b x2(t) → a y1(t) + b y2(t)
- (2) 時不変システム
- x(t) → y(t)
- のとき、任意の定数を
τ
として、
- x( t - τ) → y( t - τ)
2. 重ね合せの原理
- 「線形システム」とは、別の表現を用いれば、「重ね合せの原理」が成立するシステムです。
- この原理については、「フーリエ級数展開」の項でも述べました。
- 下の図のように、ほとんどすべての周期関数は、整数分の1の周期をもつ正弦波の重ね合せにより
- 表現できます。
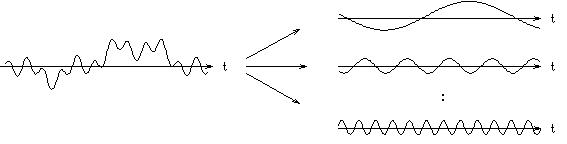
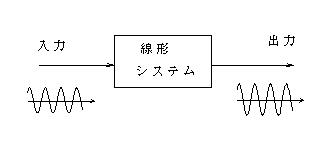
- 線形システムでは、一定の周波数成分をもつ正弦波を入力すると、その出力も同じ周波数の正弦波になります。
- ただし、振幅と位相は入力周波数とシステムの特性により変化します。
- この周波数に対する振幅と位相の特性が明らかになれば、様々な形状の波形を入力した場合の
- 出力を計算により求めることができます。
- このとき、入力と出力はその周波数に対応する線スペクトルで表現されることになります。
- 一方、理想的なインパルスは無限の周波数成分を含んでいます。(「フーリエ変換」の項を参照。)
- このインパルスは、直流から極めて高い周波数成分を有する正弦波の重ね合せにより表現することができます。
- 「線形システム」において、様々な正弦波入力に対する出力信号が既知であれば、それらの重ね合せにより
- インパルス入力に対する出力応答を求めることが可能です。
3. インパルス応答と周波数応答
- 線形システムの特性を表現する方法に、以下に示す2つの手法があります。
- 1つがインパルス応答、もう1つが周波数応答です。
- これらの概念を、以下の図に示します。
- この周波数応答では、入力となる正弦波信号の周波数が連続的に変化するスウィ-プ信号として表現していますが、
- 厳密には単一の周波数を入力した場合の出力信号の振幅と位相を、周波数毎に求めたものです。
- なお、「重ね合せの原理」の項でも述べましたが、インパルス応答と周波数応答の間にはある関係が成立します。
- その内容については後ほど検討します。
4. インパルス応答とたたみ込みの定理
-連続信号-
- ここでは、連続信号における線形システムのインパルス応答と、たたみ込みの定理について解説します。
- 入力に、単位インパルスという理想的な基準信号を与えます。
- このときの出力をインパルス入力に対する応答ということで、「インパルス応答」と呼びます。
- このインパルス応答の波形
h(t)
が既知であれば、任意の入力
x(t)
に対する出力の波形
y(t)
を計算により求める
- ことができます。
- 図の左に示す信号
x(t)
をシステムに入力します。この信号について、時間方向に細かく切れ目を入れ、
- その細長い矩形状の信号が次々に入力されるものと考えます。この矩形の幅を一様に狭くすることにより、
- 理想的なインパルスに近付けることが可能です。
- 次に、入力信号を複数のインパルスの和によって表現します。
- このインパルスは時間軸が、矩形の幅だけシフトしており、矩形の高さは入力信号の信号の大きさに一致
- するよう、
変調されているものとします。
- 先に述べた「重ね合せの原理」により、線形システムの出力
y(t)
は、それぞれの単位インパルス応答
h(τ
)
- と
入力信号の大きさ
x(t-τ)
の積を積分したものと考えることができます。
- これより、以下の式が成立します。
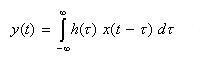
- なお、
h(τ)
と
x(t-τ)
のカッコ内の和(すなわち、
τ+ t-τ
)=
t
になっていることに注意して下さい。
- これは、時間
t
における出力の値
y(t)
は、それ以前の複数の入力
x(t-τ)
の影響が、
- h(τ)
の分だけ遅れて減衰し、それらの重ね合せとして現れているためです。
- ここで、フーリエ変換で学習したスペクトルの関係について整理しましょう。
- Y(f), X(f)
を入力と出力の信号
x(t), y(t)
のスペクトル、
H(f)
をインパルス応答
h(t)
のスペクトルとします。
- これを、次のように表現します。
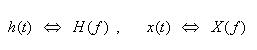
- 次に、
y(t)
を
x(t)
と
h(t)
のたたみ込みの形で表し、これをフーリエ変換します。
- このとき、次の式が成立します。
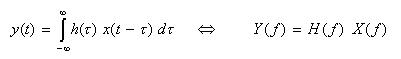
- すなわち、時間領域でたたみ込み積分の形で表された入出力の関係は、スペクトル領域では
- それらの単純な積の形で表現できることがわかります。
- 証明を以下に示します。
- [証明]
-
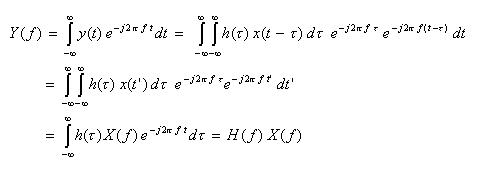
- なお,信号とスペクトルには双対性があり、以下の式が成立します。
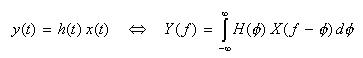
- すなわち、時間領域の積は周波数(スペクトル)の領域ではたたみ込み積分の形になります。
5. 線形システムの伝達関数 -連続信号-
- 線形システムにおいて、時間領域では複雑なたたみ込み積分で表された入出力の関係は、
- スペクトル(すなわち周波数)の領域では、単純な積の形で表現できることがわかりました。
- 言いかえれば、スペクトルを利用すれば、この線形システムの特性を極めて単純な関係式で記述することが
- 可能です。
- 上で示した関係から、
X(f)≠0
のとき次の式が導かれます。
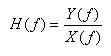
- ここで、線形システムの伝達関数
H(s)
を次のように定義します。
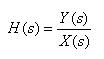
- ここで、周波数
f
を角速度
ω
で書きなおし、さらに実数部
σ
を追加した複素数
s
で表現しています。
- すなわち、以下のように拡張します。これが、いわゆるラプラス変換です。
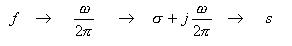
- ラプラス変換の定義式は次のようになります。
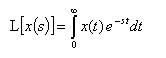
- なお、ラプラス変換の詳細については、参考書等で調べて下さい。
6. インパルス応答とたたみ込み
-離散信号-
- 連続信号の場合と同様、離散信号を対象とした線形システムでも「重ね合せの原理」が成立します。
- 離散信号においても「線形時不変システム」を定義することができます。
- 以下にその定義を示します。ただし、nは整数です。
- (1) 線形システム
- 入力
x1(n), x2(n)
出力
y1(n), y2(n)
について
- x1(n) →y1(n), x2(n) → y2(n)
- の関係が成立するとき、任意の定数を
a, b
として、
- a x1(n) + b x2(n) → a y1(n) + b y2(n)
- (2) 時不変システム
- x( n ) → y( n )
- のとき、任意の整数を
m
として、
- x( n - m) → y( n - m)
- 次に、離散信号におけるインパルス応答とたたみ込みの定理について説明します。
- 入力に、単位インパルスという理想的な基準信号を与えます。
- このときの出力をインパルスに対する応答ということで、「インパルス応答」と呼びます。
- 連続信号の場合と異なる点は、その波形が連続ではなく、離散的な出力信号になることです。
- 連続信号と同様に、このインパルス応答の波形が既知であれば、任意の入力に対する出力信号
- を求めることが可能です。
- 図の左に示す信号
x(n)
をシステムに入力します。
- 入力信号
x(n)
を複数のインパルスの和によって表現するのも、連続系の場合と同じです。
- このインパルス列は、サンプリングの周期だけずれており、時点における入力信号の大きさにより
- 変調されています。
- 先に述べた「重ね合せの原理」により、線形システムの出力
y(n)
は、それぞれの単位インパルス
- 応答
h(i)
と入力信号
x(n-i)
の積の総和として計算することができます。
- すなわち、離散信号の場合、たたみ込みの式は積分ではなく加算の形になります。
- なお、
x([n]N)
は、離散信号
x
が周期
N
の周期関数であり、循環たたみ込みにより
y
が求められる
- ことを示しています。
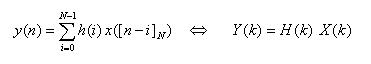
- この証明を以下に示します。
- [証明]
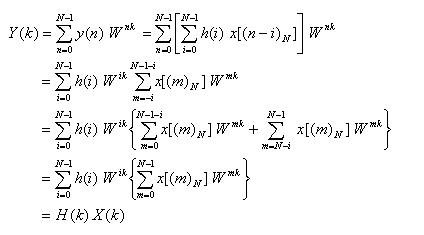
7. 線形システムの伝達関数 -離散信号-
- 線形システムにおいて、入出力の関係は、時間領域では複雑なたたみ込みの関係式で表されます。
- しかし、スペクトル(すなわち周波数)の領域では、単純な積の形で表現できます。
- 言いかえれば、スペクトルを利用すれば、この線形システムの特性を極めて単純な数式により記述する
- ことが可能です。上の式から、
X(k)≠0
のとき次式が導かれます。
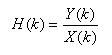
- ここで、線形システムの伝達関数
を次のように定義します。
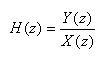
- ここで複素数
z
は、ラプラス変換の
s
を用いて次のように表されます。なお、
T
は離散信号のサンプリング周期です。
- これが、z変換です。
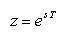
- なお、z変換の詳細については、後ほど詳しく説明します。
8. まとめ
- 本章では、線形システムの基本的な性質について整理しました。
- なお、z変換の詳細や、このシステムの応用としてのディジタルフィルタの設計方法については、次の章で解説します。
-
⇒ ディジタル信号処理(基礎編)に戻る