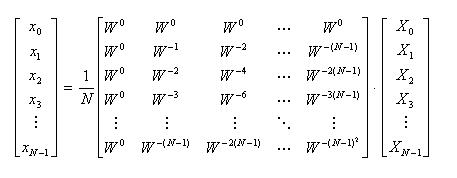高速フーリエ変換(FFT)
井澤 裕司
1. 高速フーリエ変換とは
- ここでは、高速フーリエ変換について解説します。
- 高速フーリエ変換(Fast Fourier Transform; FFT)は、離散フーリエ変換の対称性に着目して、
- その演算量を減らし高速に変換を行う手法であり、1965年、CooleyとTukeyにより発表されました。
- 周期 Nの離散フーリエ変換(DFT)では、複素数の乗算を
N2
回行う必要があります。
- 高速フーリエ変換では、その乗算回数を
N・log2N /2
回に減らすことができます。
- なお、乗算では加算を複数回行うので、加算より複雑な処理になります。
- 例えばNが2のべき乗、すなわち
N=2m
のとき、その比率を求めると、
-
[FFT] / [DFT] = m・2m-1/22m = m/2m+1
- となり、
m
(すなわち
N
)が大きいほど、その効果がはっきり現れることになります。
- 下の表に数値例を示します。
表 演算量の比較
[FFT]/ [DFT]
| N |
32 |
128 |
512 |
2048 |
| [FFT] / [DFT] |
0.078 |
0.027 |
0.0088 |
0.0027 |
- 近年のCPUには、専用の高速な乗算器が組み込まれ、加算処理との速度の差は縮まっていますが、
- 膨大な量のスペクトルを計算する場合や、リアルタイム処理が必要とされる用途では、
- この高速フーリエ変換が広く用いられています。
2. 高速フーリエ変換のアルゴリズム
- 高速フーリエ変換のアルゴリズムについて解説する前に、離散フーリエ変換(DFT)について、
- 簡単に復習しましょう。
- この変換は、周期 Nの離散信号
x(0), x(1), x(2), ‥,x(N-1)
を、同じく周期 Nの離散スペクトル
- X(0), X(1), X(2), ‥,X(N-1)
に変換するものです。
- 変換側の処理は次のように表すことができます。
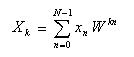
- 一方の逆変換は、次のようになります。
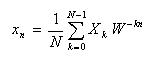
- ここで、Wは回転子と呼び、以下のように単位円をN分割した点として定義します。
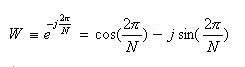
- このWについて、以下の関係が成立します。
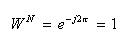
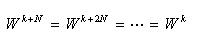
- このように、Wは k
について周期性(周期 N)があり、複素平面上で規則的な対称性をもちます。
- この性質を利用して、上で示したDFTの式を変形することにより、実質的な乗算数を減らします。
- 具体的には、AB+AC=A(B+C) のような分配則を用います。
- 対称性をより直観的に示すため、離散フーリエ変換を、マトリクス(行列)を用いて表現します。
- 変換側は次のようになります。
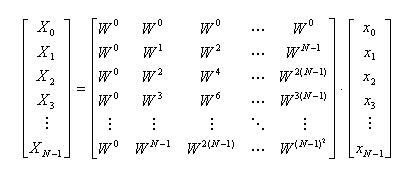
- 一方の逆変換は、次のようになります。
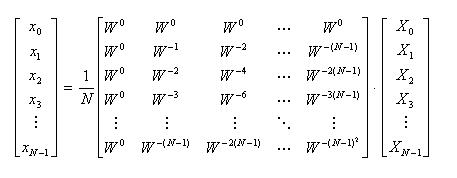
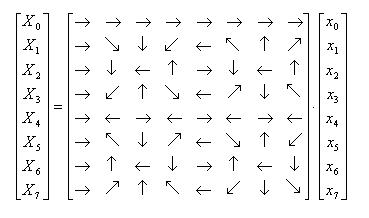
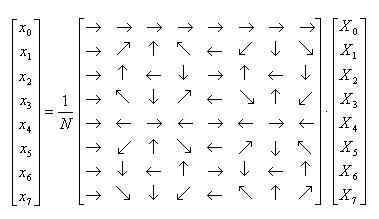
- さらに、見やすくするため、回転子Wの替わりに、→のような矢印を用いることにします。
- 例えばWは右下、W2は下、W3は左下向きの矢印で表されます。
- 例えばN=8の場合、上のマトリクスは次のようになります。
- [変換]
- [逆変換]
- これらの対称性について、詳しく調べてみましょう。
[高速フーリエ変換のアルゴリズム]
- 変換と逆変換のマトリクスは、回転の方向が違うだけで、本質的に同じような対称性があります。
- そこで、変換側の演算の対称性について、次のツールを用いて検討します。
- はじめは、ステージは「始め」の位置にあります。
- 「次」を1回クリックして、次のステージに進みます。
- ここで、ベクトルとマトリクスの奇数行と偶数行に注目してください。
- 奇数行には斜めの成分が含まれていません。
- そこで、行の入れ替えを行い、奇数行と偶数行を別々に処理することにします。(次をクリック)
- その結果、ベクトルは(4×1)、マトリクスは(4×8)となります。
- ここで、マトリクスの対称性に注目して下さい。(赤と青で色分け)
- 例えば上のマトリクスでは、右半分と左半分が同じ形をしています。
- 一方、下のマトリクスでは、右半分にマイナスをつけたものが左半分になっています。(次をクリック)
- そこで、マトリクスの右半分を左半分で代用することを考えます。
- 信号 x0 ~ x7について、加算もしくは減算を行ってから、(4×4)のマトリクスをかけます。
- この過程は、いわゆる分配則を用いて因数分解する操作に等価です。(次をクリック)
- このようにして、(4×1)のベクトルと(4×4)のマトリクスをかける演算に置き替えることができました。
- この結果、乗算数は約1/2に減少しています。
- 次に、2つの(4×4)のマトリクスに着目して下さい。これらにも、まだ対称性が残っています。(次をクリック)
- 先ほどと同じようにマトリクスの奇数行と偶数行に規則性が見られます。そこでこれらを分離して計算します。
- 今度は、(2×1)のベクトル、(2×4)のマトリクスを用いた4つの式が生成されました。
- これらのマトリクスの左右を見比べて下さい。左右が全く等しい場合と、90°、180°、270°回転させた
- 関係になっていることがわかります。(次をクリック)
- 先ほどと同様に、マトリクスの右半分を左半分で代用します。
- 具体的には、ベクトルの演算を行ってから、左半分のマトリクスを乗じます。(次をクリック)
- 最終的には、(2×1)のベクトル、(2×2)のマトリクスを用いた4つの式が生成されました。
- この計算で
[
→] (
×W0)
は実質何もしません。
- また、
[
←] (
×W4)
は-1をかける操作であり、加算が減算(あるいはその逆)になるだけです。
- このため実質的な乗算数は10となり、何もしない通常のDFTの64に対し、約1/6に減少していることが
- わかります。
3. 高速フーリエ変換の表現 -バタフライ-
- 上で定義した高速フーリエ変換を、「バタフライ」という図形を用いて表現することが可能です。
- このような表現を用いることにより、高速フーリエ変換のアルゴリズムを幾何学的に記述することができます。
- バタフライとは、2つの入力と出力を持つ演算の単位であり、最も単純なバタフライは、2つの入力の和と差を
- 出力するものです。
- 2つの三角形で構成され、形が蝶々(Butterfly)に似ていることからバタフライと呼ばれます。
- 下のツールは、先に求めたFFTのアルゴリズムを表しています。
- 図の小さな三角形は、入力信号の値に定数をかけて出力する乗算素子です。
- 左下のボタンを操作することにより、ステ-ジを移動することができます。
- ステージ毎に、対応する信号と図形の関連を色を用いて表現していますので、上で説明したアルゴリズムが実現される
- 過程を復習して下さい。
4. まとめ
- 本章では、高速フーリエ変換について学習しました。
- このFFTには、様々な実現手法が存在します。それらについては、文献等で調べて見て下さい。
-
⇒ ディジタル信号処理(基礎編)に戻る